Kaluza–Klein theory

From Wikipedia, the free encyclopedia

In physics, Kaluza–Klein theory (KK theory) is a classical unified field theory of gravitation and electromagnetism built around the idea of a fifth dimension beyond the usual four of space and time and considered an important precursor to string theory.

The five-dimensional theory developed in three steps. The original hypothesis came from Theodor Kaluza, who sent his results to Einstein in 1919,^[1] and published them in 1921,^[2] which detailed a purely classical extension of general relativity to five dimensions and includes 15 components. Ten components are identified with the four-dimensional spacetime metric, four components with the electromagnetic vector potential, and one component with an unidentified scalar field sometimes called the "radion" or the "dilaton". Correspondingly, the five-dimensional Einstein equations yield the four-dimensional Einstein field equations, the Maxwell equations for the electromagnetic field, and an equation for the scalar field. Kaluza also introduced the "cylinder condition" hypothesis, that no component of the five-dimensional metric depends on the fifth dimension. Without this assumption, the field equations of five-dimensional relativity grow enormous in complexity. Standard four-dimensional physics seems to manifest the cylinder condition.

In 1926, Oskar Klein gave Kaluza's classical five-dimensional theory a quantum interpretation,^[3][4] to accord with the then-recent discoveries of Heisenberg and Schrödinger. Klein introduced the hypothesis that the fifth dimension was curled up and microscopic, to explain the cylinder condition. Klein suggested that the geometry of the extra fifth dimension could take the form of a circle, with the radius of 10⁻³⁰ cm.^[5] Klein also calculated a scale for the fifth dimension based on the quantum of charge.

In the 1940s the classical theory was completed, and the full field equations including the scalar field were obtained by three independent research groups:^[6] Thiry,^[7][8][9] working in France on his dissertation under Lichnerowicz; Jordan, Ludwig, and Müller in Germany,^{[10][11][12][13][14]} with critical input from Pauli and Fierz; and Scherrer ^[15][16][17] working alone in Switzerland. Jordan's work led to the scalar-tensor theory of Brans–Dicke;^[18] Brans and Dicke were apparently unaware of Thiry or Scherrer. The full Kaluza equations under the cylinder condition are quite complex, and most English-language reviews as well as the English translations of Thiry contain some errors. The complete Kaluza equations were evaluated^{[clarification needed]} using tensor algebra software in 2015.^[19]

Kaluza hypothesis

In his 1921 paper,^[2] Kaluza established all the elements of the classical five-dimensional theory: the metric, the field equations, the equations of motion, the stress-energy tensor, and the cylinder condition. With no free parameters, it merely extends general relativity to five dimensions. One starts by hypothesizing a form of the five-dimensional metric ${\displaystyle {\widetilde {g}}_{ab}}$, where Latin indices span five dimensions. Let one also introduce the four-dimensional spacetime metric ${\displaystyle {g}_{\mu \nu }}$, where Greek indices span the usual four dimensions of space and time; a 4-vector ${\displaystyle A^{\mu }}$ identified with the electromagnetic vector potential; and a scalar field ${\displaystyle \phi }$. Then decompose the 5D metric so that the 4D metric is framed by the electromagnetic vector potential, with the scalar field at the fifth diagonal. This can be visualized as:

${\displaystyle {\widetilde {g}}_{ab}\equiv {\begin{bmatrix}g_{\mu \nu }+\phi ^{2}A_{\mu }A_{\nu }&\phi ^{2}A_{\mu }\\\phi ^{2}A_{\nu }&\phi ^{2}\end{bmatrix}}}$.

One can write more precisely

${\displaystyle {\widetilde {g}}_{\mu \nu }\equiv g_{\mu \nu }+\phi ^{2}A_{\mu }A_{\nu },\qquad {\widetilde {g}}_{5\nu }\equiv {\widetilde {g}}_{\nu 5}\equiv \phi ^{2}A_{\nu },\qquad {\widetilde {g}}_{55}\equiv \phi ^{2}}$

where the index ${\displaystyle 5}$ indicates the fifth coordinate by convention even though the first four coordinates are indexed with 0, 1, 2, and 3. The associated inverse metric is

${\displaystyle {\widetilde {g}}^{ab}\equiv {\begin{bmatrix}g^{\mu \nu }&-A^{\mu }\\-A^{\nu }&g_{\alpha \beta }A^{\alpha }A^{\beta }+{1 \over \phi ^{2}}\end{bmatrix}}}$.

This decomposition is quite general and all terms dimensionless. Kaluza then applies the machinery of standard general relativity to this metric. The field equations are obtained from five-dimensional Einstein equations, and the equations of motion from the five-dimensional geodesic hypothesis. The resulting field equations provide both the equations of general relativity and of electrodynamics; the equations of motion provide the four-dimensional geodesic equation and the Lorentz force law, and one finds that electric charge is identified with motion in the fifth dimension.

The hypothesis for the metric implies an invariant five-dimensional length element ${\displaystyle \operatorname {d} \!s}$:

${\displaystyle \operatorname {d} \!s^{2}\equiv {\widetilde {g}}_{ab}\operatorname {d} \!x^{a}\operatorname {d} \!x^{b}=g_{\mu \nu }dx^{\mu }\operatorname {d} \!x^{\nu }+\phi ^{2}(A_{\nu }\operatorname {d} \!x^{\nu }+\operatorname {d} \!x^{5})^{2}}$

 

Field equations from the Kaluza hypothesis

The field equations of the 5-dimensional theory were never adequately provided by Kaluza or Klein, mainly regarding the scalar field. The full Kaluza field equations are generally attributed to Thiry,^[8] who obtained vacuum field equations, although Kaluza ^[2] originally provided a stress-energy tensor for his theory and Thiry included a stress-energy tensor in his thesis. But as described by Gonner,^[6] several independent groups worked on the field equations in the 1940s and earlier. Thiry is perhaps best known only because an English translation was provided by Applequist, Chodos, & Freund in their review book.^[20] Applequist et al. also provided an English translation of Kaluza's paper. There are no English translations of the Jordan papers.^[10][11][13]

To obtain the 5D field equations, the 5D connections ${\displaystyle {\widetilde {\Gamma }}_{bc}^{a}}$ are calculated from the 5D metric ${\displaystyle {\widetilde {g}}_{ab}}$, and the 5D Ricci tensor ${\displaystyle {\widetilde {R}}_{ab}}$ is calculated from the 5D connections.

The classic results of Thiry and other authors presume the cylinder condition:

${\displaystyle {\partial {\widetilde {g}}_{ab} \over \partial x^{5}}=0}$.

Without this assumption, the field equations become much more complex, providing many more degrees of freedom that can be identified with various new fields. Paul Wesson and colleagues have pursued relaxation of the cylinder condition to gain extra terms that can be identified with the matter fields,^[21] for which Kaluza ^[2] otherwise inserted a stress-energy tensor by hand.

It has been an objection to the original Kaluza hypothesis to invoke the fifth dimension only to negate its dynamics. But Thiry argued ^[6] that the interpretation of the Lorentz force law in terms of a 5-dimensional geodesic militates strongly for a fifth dimension irrespective of the cylinder condition. Most authors have therefore employed the cylinder condition in deriving the field equations. Furthermore, vacuum equations are typically assumed for which

${\displaystyle {\widetilde {R}}_{ab}=0}$

where

${\displaystyle {\widetilde {R}}_{ab}\equiv \partial _{c}{\widetilde {\Gamma }}_{ab}^{c}-\partial _{b}{\widetilde {\Gamma }}_{ca}^{c}+{\widetilde {\Gamma }}_{cd}^{c}{\widetilde {\Gamma }}_{ab}^{d}-{\widetilde {\Gamma }}_{bd}^{c}{\widetilde {\Gamma }}_{ac}^{d}}$

and

${\displaystyle {\widetilde {\Gamma }}_{bc}^{a}\equiv {1 \over 2}{\widetilde {g}}^{ad}(\partial _{b}{\widetilde {g}}_{dc}+\partial _{c}{\widetilde {g}}_{db}-\partial _{d}{\widetilde {g}}_{bc})}$

The vacuum field equations obtained in this way by Thiry ^[8] and Jordan's group ^[10][11][13] are as follows.

The field equation for ${\displaystyle \phi }$ is obtained from

${\displaystyle {\widetilde {R}}_{55}=0\Rightarrow \Box \phi ={1 \over 4}\phi ^{3}F^{\alpha \beta }F_{\alpha \beta }}$

where ${\displaystyle F_{\alpha \beta }\equiv \partial _{\alpha }A_{\beta }-\partial _{\beta }A_{\alpha }}$, where ${\displaystyle \Box \equiv g^{\mu \nu }\nabla _{\mu }\nabla _{\nu }}$, and where ${\displaystyle \nabla _{\mu }}$ is a standard, 4D covariant derivative. It shows that the electromagnetic field is a source for the scalar field. Note that the scalar field cannot be set to a constant without constraining the electromagnetic field. The earlier treatments by Kaluza and Klein did not have an adequate description of the scalar field, and did not realize the implied constraint on the electromagnetic field by assuming the scalar field to be constant.

The field equation for ${\displaystyle A^{\nu }}$ is obtained from

${\displaystyle {\widetilde {R}}_{5\alpha }=0={1 \over 2}g^{\beta \mu }\nabla _{\mu }(\phi ^{3}F_{\alpha \beta })}$

It has the form of the vacuum Maxwell equations if the scalar field is constant.

The field equation for the 4D Ricci tensor ${\displaystyle R_{\mu \nu }}$ is obtained from

${\displaystyle {\begin{aligned}{\widetilde {R}}_{\mu \nu }-{1 \over 2}{\widetilde {g}}_{\mu \nu }{\widetilde {R}}&=0\Rightarrow \\R_{\mu \nu }-{1 \over 2}g_{\mu \nu }R&={1 \over 2}\phi ^{2}\left(g^{\alpha \beta }F_{\mu \alpha }F_{\nu \beta }-{1 \over 4}g_{\mu \nu }F_{\alpha \beta }F^{\alpha \beta }\right)+{1 \over \phi }\left(\nabla _{\mu }\nabla _{\nu }\phi -g_{\mu \nu }\Box \phi \right)\end{aligned}}}$

where ${\displaystyle R}$ is the standard 4D Ricci scalar.

This equation shows the remarkable result, called the "Kaluza miracle", that the precise form for the electromagnetic stress-energy tensor emerges from the 5D vacuum equations as a source in the 4D equations: field from the vacuum. This relation allows the definitive identification of ${\displaystyle A^{\mu }}$ with the electromagnetic vector potential. Therefore, the field needs to be rescaled with a conversion constant ${\displaystyle k}$ such that ${\displaystyle A^{\mu }\rightarrow kA^{\mu }}$.

The relation above shows that we must have

${\displaystyle {k^{2} \over 2}={8\pi G \over c^{4}}{1 \over \mu _{0}}={2G \over c^{2}}{4\pi \epsilon _{0}}}$

where ${\displaystyle G}$ is the gravitational constant and ${\displaystyle \mu _{0}}$ is the permeability of free space. In the Kaluza theory, the gravitational constant can be understood as an electromagnetic coupling constant in the metric. There is also a stress-energy tensor for the scalar field. The scalar field behaves like a variable gravitational constant, in terms of modulating the coupling of electromagnetic stress energy to spacetime curvature. The sign of ${\displaystyle \phi ^{2}}$ in the metric is fixed by correspondence with 4D theory so that electromagnetic energy densities are positive. This turns out to imply that the 5th coordinate is spacelike in its signature in the metric.

In the presence of matter, the 5D vacuum condition can not be assumed. Indeed, Kaluza did not assume it. The full field equations require evaluation of the 5D Einstein tensor

${\displaystyle {\widetilde {G}}_{ab}\equiv {\widetilde {R}}_{ab}-{1 \over 2}{\widetilde {g}}_{ab}{\widetilde {R}}}$

as seen in the recovery of the electromagnetic stress-energy tensor above. The 5D curvature tensors are complex, and most English-language reviews contain errors in either ${\displaystyle {\widetilde {G}}_{ab}}$ or ${\displaystyle {\widetilde {R}}_{ab}}$, as does the English translation of.^[8] See ^[19] for a complete set of 5D curvature tensors under the cylinder condition, evaluated using tensor algebra software.

Equations of motion from the Kaluza hypothesis

The equations of motion are obtained from the five-dimensional geodesic hypothesis ^[2] in terms of a 5-velocity ${\displaystyle {\widetilde {U}}^{a}\equiv dx^{a}/ds}$:

${\displaystyle {\widetilde {U}}^{b}{\widetilde {\nabla }}_{b}{\widetilde {U}}^{a}={d{\widetilde {U}}^{a} \over ds}+{\widetilde {\Gamma }}_{bc}^{a}{\widetilde {U}}^{b}{\widetilde {U}}^{c}=0}$

This equation can be recast in several ways, and it has been studied in various forms by authors including Kaluza,^[2] Pauli,^[22] Gross & Perry,^[23] Gegenberg & Kunstatter,^[24] and Wesson & Ponce de Leon,^[25] but it is instructive to convert it back to the usual 4-dimensional length element ${\displaystyle c^{2}d\tau ^{2}\equiv g_{\mu \nu }dx^{\mu }dx^{\nu }}$, which is related to the 5-dimensional length element ${\displaystyle ds}$ as given above:

${\displaystyle ds^{2}=c^{2}d\tau ^{2}+\phi ^{2}(kA_{\nu }dx^{\nu }+dx^{5})^{2}}$

Then the 5D geodesic equation can be written ^[26] for the spacetime components of the 4velocity, ${\displaystyle U^{\nu }\equiv dx^{\nu }/d\tau }$:

 ${\displaystyle {dU^{\nu } \over d\tau }+{\widetilde {\Gamma }}_{\alpha \beta }^{\mu }U^{\alpha }U^{\beta }+2{\widetilde {\Gamma }}_{5\alpha }^{\mu }U^{\alpha }U^{5}+{\widetilde {\Gamma }}_{55}^{\mu }(U^{5})^{2}+U^{\mu }{d \over d\tau }\ln \left({cd\tau \over ds}\right)=0}$

The term quadratic in ${\displaystyle U^{\nu }}$ provides the 4D geodesic equation plus some electromagnetic terms:

${\displaystyle {\widetilde {\Gamma }}_{\alpha \beta }^{\mu }=\Gamma _{\alpha \beta }^{\mu }+{1 \over 2}g^{\mu \nu }k^{2}\phi ^{2}(A_{\alpha }F_{\beta \nu }+A_{\beta }F_{\alpha \nu }+A_{\alpha }A_{\beta }\partial _{\nu }\ln \phi ^{2})}$

The term linear in ${\displaystyle U^{\nu }}$ provides the Lorentz force law:

${\displaystyle {\widetilde {\Gamma }}_{5\alpha }^{\mu }={1 \over 2}g^{\mu \nu }k\phi ^{2}(F_{\alpha \nu }-A_{\alpha }\partial _{\nu }\ln \phi ^{2})}$

This is another expression of the "Kaluza miracle". The same hypothesis for the 5D metric that provides electromagnetic stress-energy in the Einstein equations, also provides the Lorentz force law in the equation of motions along with the 4D geodesic equation. Yet correspondence with the Lorentz force law requires that we identify the component of 5-velocity along the 5th dimension with electric charge:

${\displaystyle kU^{5}=k{dx^{5} \over d\tau }\rightarrow {q \over mc}}$

where ${\displaystyle m}$ is particle mass and ${\displaystyle q}$ is particle electric charge. Thus, electric charge is understood as motion along the 5th dimension. The fact that the Lorentz force law could be understood as a geodesic in 5 dimensions was to Kaluza a primary motivation for considering the 5-dimensional hypothesis, even in the presence of the aesthetically-unpleasing cylinder condition.

Yet there is a problem: the term quadratic in ${\displaystyle U^{5}}$.

${\displaystyle {\widetilde {\Gamma }}_{55}^{\mu }=-{1 \over 2}g^{\mu \alpha }\partial _{\alpha }\phi ^{2}}$

If there is no gradient in the scalar field, the term quadratic in ${\displaystyle U^{5}}$ vanishes. But otherwise the expression above implies

${\displaystyle U^{5}\sim c{q/m \over G^{1/2}}}$

For elementary particles, ${\displaystyle U^{5}>{\rm {10}}^{20}c}$. The term quadratic in ${\displaystyle U^{5}}$ should dominate the equation, perhaps in contradiction to experience. This was the main shortfall of the 5-dimensional theory as Kaluza saw it,^[2] and he gives it some discussion in his original article.

The equation of motion for ${\displaystyle U^{5}}$ is particularly simple under the cylinder condition. Start with the alternate form of the geodesic equation, written for the covariant 5-velocity:

${\displaystyle {d{\widetilde {U}}_{a} \over ds}={1 \over 2}{\widetilde {U}}^{b}{\widetilde {U}}^{c}{\partial {\widetilde {g}}_{bc} \over \partial x^{a}}}$

This means that under the cylinder condition, ${\displaystyle {\widetilde {U}}_{5}}$ is a constant of the 5-dimensional motion:

${\displaystyle {\widetilde {U}}_{5}={\widetilde {g}}_{5a}{\widetilde {U}}^{a}=\phi ^{2}{cd\tau \over ds}(kA_{\nu }U^{\nu }+U^{5})={\rm {constant}}}$

Kaluza's hypothesis for the matter stress-energy tensor

Kaluza ^[2] proposed a 5D matter stress tensor ${\displaystyle {\widetilde {T}}_{M}^{ab}}$ of the form

${\displaystyle {\widetilde {T}}_{M}^{ab}=\rho {dx^{a} \over ds}{dx^{b} \over ds}}$

where ${\displaystyle \rho }$ is a density and the length element ${\displaystyle ds}$ is as defined above.

Then, the spacetime component gives a typical "dust" stress energy tensor:

${\displaystyle {\widetilde {T}}_{M}^{\mu \nu }=\rho {dx^{\mu } \over ds}{dx^{\nu } \over ds}}$

The mixed component provides a 4-current source for the Maxwell equations:

${\displaystyle {\widetilde {T}}_{M}^{5\mu }=\rho {dx^{\mu } \over ds}{dx^{5} \over ds}=\rho U^{\mu }{q \over kmc}}$

Just as the five-dimensional metric comprises the 4-D metric framed by the electromagnetic vector potential, the 5-dimensional stress-energy tensor comprises the 4-D stress-energy tensor framed by the vector 4-current.

Quantum interpretation of Klein

Kaluza's original hypothesis was purely classical and extended discoveries of general relativity. By the time of Klein's contribution, the discoveries of Heisenberg, Schrödinger, and de Broglie were receiving a lot of attention. Klein's Nature paper ^[4] suggested that the fifth dimension is closed and periodic, and that the identification of electric charge with motion in the fifth dimension be interpreted as standing waves of wavelength ${\displaystyle \lambda ^{5}}$, much like the electrons around a nucleus in the Bohr model of the atom. The quantization of electric charge could then be nicely understood in terms of integer multiples of fifth-dimensional momentum. Combining the previous Kaluza result for ${\displaystyle U^{5}}$ in terms of electric charge, and a de Broglie relation for momentum ${\displaystyle p^{5}=h/\lambda ^{5}}$, Klein ^[4] obtained an expression for the 0th mode of such waves:

${\displaystyle mU^{5}={cq \over G^{1/2}}={h \over \lambda ^{5}}\qquad \Rightarrow \qquad \lambda ^{5}\sim {hG^{1/2} \over cq}}$

where ${\displaystyle h}$ is the Planck constant. Klein found ${\displaystyle \lambda ^{5}\sim {\rm {10}}^{-30}}$ cm, and thereby an explanation for the cylinder condition in this small value.

Klein's Zeitschrift für Physik paper of the same year,^[3] gave a more-detailed treatment that explicitly invoked the techniques of Schroedinger and de Broglie. It recapitulated much of the classical theory of Kaluza described above, and then departed into Klein's quantum interpretation. Klein solved a Schroedinger-like wave equation using an expansion in terms of fifth-dimensional waves resonating in the closed, compact fifth dimension.

Quantum field theory interpretation

Group theory interpretation

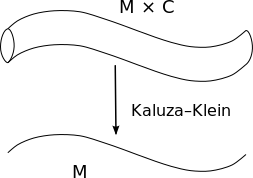
The space M × C is compactified over the compact set C, and after Kaluza–Klein decomposition one has an effective field theory over M.

A splitting of five-dimensional spacetime into the Einstein equations and Maxwell equations in four dimensions was first discovered by Gunnar Nordström in 1914, in the context of his theory of gravity, but subsequently forgotten. Kaluza published his derivation in 1921 as an attempt to unify electromagnetism with Einstein's general relativity.

In 1926, Oskar Klein proposed that the fourth spatial dimension is curled up in a circle of a very small radius, so that a particle moving a short distance along that axis would return to where it began. The distance a particle can travel before reaching its initial position is said to be the size of the dimension. This extra dimension is a compact set, and construction of this compact dimension is referred to as compactification.

In modern geometry, the extra fifth dimension can be understood to be the circle group U(1), as electromagnetism can essentially be formulated as a gauge theory on a fiber bundle, the circle bundle, with gauge group U(1). In Kaluza–Klein theory this group suggests that gauge symmetry is the symmetry of circular compact dimensions. Once this geometrical interpretation is understood, it is relatively straightforward to replace U(1) by a general Lie group. Such generalizations are often called Yang–Mills theories. If a distinction is drawn, then it is that Yang–Mills theories occur on a flat space-time, whereas Kaluza–Klein treats the more general case of curved spacetime. The base space of Kaluza–Klein theory need not be four-dimensional space-time; it can be any (pseudo-)Riemannian manifold, or even a supersymmetric manifold or orbifold or even a noncommutative space.

The construction can be outlined, roughly, as follows.^[27] One starts by considering a principal fiber bundle P with gauge group G over a manifold M. Given a connection on the bundle, and a metric on the base manifold, and a gauge invariant metric on the tangent of each fiber, one can construct a bundle metric defined on the entire bundle. Computing the scalar curvature of this bundle metric, one finds that it is constant on each fiber: this is the "Kaluza miracle". One did not have to explicitly impose a cylinder condition, or to compactify: by assumption, the gauge group is already compact. Next, one takes this scalar curvature as the Lagrangian density, and, from this, constructs the Einstein–Hilbert action for the bundle, as a whole. The equations of motion, the Euler–Lagrange equations, can be then obtained by considering where the action is stationary with respect to variations of either the metric on the base manifold, or of the gauge connection. Variations with respect to the base metric gives the Einstein field equations on the base manifold, with the energy-momentum tensor given by the curvature (field strength) of the gauge connection. On the flip side, the action is stationary against variations of the gauge connection precisely when the gauge connection solves the Yang-Mills equations. Thus, by applying a single idea: the principle of least action, to a single quantity: the scalar curvature on the bundle (as a whole), one obtains simultaneously all of the needed field equations, for both the space-time and the gauge field.

As an approach to the unification of the forces, it is straightforward to apply the Kaluza–Klein theory in an attempt to unify gravity with the strong and electroweak forces by using the symmetry group of the Standard Model, SU(3) × SU(2) × U(1). However, an attempt to convert this interesting geometrical construction into a bona-fide model of reality founders on a number of issues, including the fact that the fermions must be introduced in an artificial way (in nonsupersymmetric models). Nonetheless, KK remains an important touchstone in theoretical physics and is often embedded in more sophisticated theories. It is studied in its own right as an object of geometric interest in K-theory.

Even in the absence of a completely satisfying theoretical physics framework, the idea of exploring extra, compactified, dimensions is of considerable interest in the experimental physics and astrophysics communities. A variety of predictions, with real experimental consequences, can be made (in the case of large extra dimensions and warped models). For example, on the simplest of principles, one might expect to have standing waves in the extra compactified dimension(s). If a spatial extra dimension is of radius R, the invariant mass of such standing waves would be M_n = nh/Rc with n an integer, h being Planck's constant and c the speed of light. This set of possible mass values is often called the Kaluza–Klein tower. Similarly, in Thermal quantum field theory a compactification of the euclidean time dimension leads to the Matsubara frequencies and thus to a discretized thermal energy spectrum.

However, Klein's approach to a quantum theory is flawed and, for example, leads to a calculated electron mass of 3×(10³⁰) MeV instead of the measured value 0.511 MeV.

Examples of experimental pursuits include work by the CDF collaboration, which has re-analyzed particle collider data for the signature of effects associated with large extra dimensions/warped models.

Brandenberger and Vafa have speculated that in the early universe, cosmic inflation causes three of the space dimensions to expand to cosmological size while the remaining dimensions of space remained microscopic.

Space–time–matter theory

One particular variant of Kaluza–Klein theory is space–time–matter theory or induced matter theory, chiefly promulgated by Paul Wesson and other members of the Space–Time–Matter Consortium.^[28] In this version of the theory, it is noted that solutions to the equation

${\displaystyle {\widetilde {R}}_{ab}=0}$

may be re-expressed so that in four dimensions, these solutions satisfy Einstein's equations

${\displaystyle G_{\mu \nu }=8\pi T_{\mu \nu }\,}$

with the precise form of the T_μν following from the Ricci-flat condition on the five-dimensional space. In other words, the cylinder condition of the previous development is dropped, and the stress–energy now comes from the derivatives of the 5D metric with respect to the fifth coordinate. Because the energy–momentum tensor is normally understood to be due to concentrations of matter in four-dimensional space, the above result is interpreted as saying that four-dimensional matter is induced from geometry in five-dimensional space.

In particular, the soliton solutions of ${\displaystyle {\widetilde {R}}_{ab}=0}$ can be shown to contain the Friedmann–Lemaître–Robertson–Walker metric in both radiation-dominated (early universe) and matter-dominated (later universe) forms. The general equations can be shown to be sufficiently consistent with classical tests of general relativity to be acceptable on physical principles, while still leaving considerable freedom to also provide interesting cosmological models.

Geometric interpretation

The Kaluza–Klein theory has a particularly elegant presentation in terms of geometry. In a certain sense, it looks just like ordinary gravity in free space, except that it is phrased in five dimensions instead of four.

Einstein equations

The equations governing ordinary gravity in free space can be obtained from an action, by applying the variational principle to a certain action. Let M be a (pseudo-)Riemannian manifold, which may be taken as the spacetime of general relativity. If g is the metric on this manifold, one defines the action S(g) as

${\displaystyle S(g)=\int _{M}R(g)\mathrm {vol} (g)\,}$

where R(g) is the scalar curvature and vol(g) is the volume element. By applying the variational principle to the action

${\displaystyle {\frac {\delta S(g)}{\delta g}}=0}$

one obtains precisely the Einstein equations for free space:

${\displaystyle R_{ij}-{\frac {1}{2}}g_{ij}R=0}$

Here, R_ij is the Ricci tensor.

Maxwell equations

By contrast, the Maxwell equations describing electromagnetism can be understood to be the Hodge equations of a principal U(1)-bundle or circle bundle π: P → M with fiber U(1). That is, the electromagnetic field F is a harmonic 2-form in the space Ω²(M) of differentiable 2-forms on the manifold M. In the absence of charges and currents, the free-field Maxwell equations are

dF = 0 and d*F = 0.

where * is the Hodge star.

Kaluza–Klein geometry

To build the Kaluza–Klein theory, one picks an invariant metric on the circle S¹ that is the fiber of the U(1)-bundle of electromagnetism. In this discussion, an invariant metric is simply one that is invariant under rotations of the circle. Suppose this metric gives the circle a total length of Λ. One then considers metrics ${\displaystyle {\widehat {g}}}$ on the bundle P that are consistent with both the fiber metric, and the metric on the underlying manifold M. The consistency conditions are:

• The projection of ${\displaystyle {\widehat {g}}}$ to the vertical subspace ${\displaystyle {\mbox{Vert}}_{p}P\subset T_{p}P}$ needs to agree with metric on the fiber over a point in the manifold M.
• The projection of ${\displaystyle {\widehat {g}}}$ to the horizontal subspace ${\displaystyle {\mbox{Hor}}_{p}P\subset T_{p}P}$ of the tangent space at point p ∈ P must be isomorphic to the metric g on M at π(p).

The Kaluza–Klein action for such a metric is given by

${\displaystyle S({\widehat {g}})=\int _{P}R({\widehat {g}})\;{\mbox{vol}}({\widehat {g}})\,}$

The scalar curvature, written in components, then expands to

${\displaystyle R({\widehat {g}})=\pi ^{*}\left(R(g)-{\frac {\Lambda ^{2}}{2}}\vert F\vert ^{2}\right)}$

where π* is the pullback of the fiber bundle projection π: P → M. The connection A on the fiber bundle is related to the electromagnetic field strength as

${\displaystyle \pi ^{*}F=\mathrm {d} A}$

That there always exists such a connection, even for fiber bundles of arbitrarily complex topology, is a result from homology and specifically, K-theory. Applying Fubini's theorem and integrating on the fiber, one gets

${\displaystyle S({\widehat {g}})=\Lambda \int _{M}\left(R(g)-{\frac {1}{\Lambda ^{2}}}\vert F\vert ^{2}\right)\;{\mbox{vol}}(g)}$

Varying the action with respect to the component A, one regains the Maxwell equations. Applying the variational principle to the base metric g, one gets the Einstein equations

${\displaystyle R_{ij}-{\frac {1}{2}}g_{ij}R={\frac {1}{\Lambda ^{2}}}T_{ij}}$

with the stress–energy tensor being given by

${\displaystyle T^{ij}=F^{ik}F^{jl}g_{kl}-{\frac {1}{4}}g^{ij}\vert F\vert ^{2},}$

sometimes called the Maxwell stress tensor.

The original theory identifies Λ with the fiber metric g₅₅, and allows Λ to vary from fiber to fiber. In this case, the coupling between gravity and the electromagnetic field is not constant, but has its own dynamical field, the radion.

Generalizations

In the above, the size of the loop Λ acts as a coupling constant between the gravitational field and the electromagnetic field. If the base manifold is four-dimensional, the Kaluza–Klein manifold P is five-dimensional. The fifth dimension is a compact space, and is called the compact dimension. The technique of introducing compact dimensions to obtain a higher-dimensional manifold is referred to as compactification. Compactification does not produce group actions on chiral fermions except in very specific cases: the dimension of the total space must be 2 mod 8 and the G-index of the Dirac operator of the compact space must be nonzero.^[29]

The above development generalizes in a more-or-less straightforward fashion to general principal G-bundles for some arbitrary Lie group G taking the place of U(1). In such a case, the theory is often referred to as a Yang–Mills theory, and is sometimes taken to be synonymous. If the underlying manifold is supersymmetric, the resulting theory is a super-symmetric Yang–Mills theory.

Empirical tests

No experimental or observational signs of extra dimensions have been officially reported. Many theoretical search techniques for detecting Kaluza–Klein resonances have been proposed using the mass couplings of such resonances with the top quark. However, until the Large Hadron Collider (LHC) reaches full operational power, observation of such resonances are unlikely. An analysis of results from the LHC in December 2010 severely constrains theories with large extra dimensions.^[30]

The observation of a Higgs-like boson at the LHC establishes a new empirical test which can be applied to the search for Kaluza–Klein resonances and supersymmetric particles. The loop Feynman diagrams that exist in the Higgs interactions allow any particle with electric charge and mass to run in such a loop. Standard Model particles besides the top quark and W boson do not make big contributions to the cross-section observed in the H → γγ decay, but if there are new particles beyond the Standard Model, they could potentially change the ratio of the predicted Standard Model H → γγ cross-section to the experimentally observed cross-section. Hence a measurement of any dramatic change to the H → γγ cross section predicted by the Standard Model is crucial in probing the physics beyond it.