Predictive analytics

From Wikipedia, the free encyclopedia

Predictive analytics encompasses a variety of statistical techniques from data mining, predictive modelling, and machine learning, that analyze current and historical facts to make predictions about future or otherwise unknown events.

In business, predictive models exploit patterns found in historical and transactional data to identify risks and opportunities. Models capture relationships among many factors to allow assessment of risk or potential associated with a particular set of conditions, guiding decision making for candidate transactions.

The defining functional effect of these technical approaches is that predictive analytics provides a predictive score (probability) for each individual (customer, employee, healthcare patient, product SKU, vehicle, component, machine, or other organizational unit) in order to determine, inform, or influence organizational processes that pertain across large numbers of individuals, such as in marketing, credit risk assessment, fraud detection, manufacturing, healthcare, and government operations including law enforcement.

Predictive analytics is used in actuarial science, marketing, financial services, insurance, telecommunications, retail, travel, mobility,  healthcare, child protection, pharmaceuticals, capacity planning, social networking and other fields.

One of the best-known applications is credit scoring, which is used throughout financial services. Scoring models process a customer's credit history, loan application, customer data, etc., in order to rank-order individuals by their likelihood of making future credit payments on time.

Definition

Predictive analytics is an area of statistics that deals with extracting information from data and using it to predict trends and behavior patterns. The enhancement of predictive web analytics calculates statistical probabilities of future events online. Predictive analytics statistical techniques include data modeling, machine learning, AI, deep learning algorithms and data mining. Often the unknown event of interest is in the future, but predictive analytics can be applied to any type of unknown whether it be in the past, present or future. For example, identifying suspects after a crime has been committed, or credit card fraud as it occurs. The core of predictive analytics relies on capturing relationships between explanatory variables and the predicted variables from past occurrences, and exploiting them to predict the unknown outcome. It is important to note, however, that the accuracy and usability of results will depend greatly on the level of data analysis and the quality of assumptions.

Predictive analytics is often defined as predicting at a more detailed level of granularity, i.e., generating predictive scores (probabilities) for each individual organizational element. This distinguishes it from forecasting. For example, "Predictive analytics—Technology that learns from experience (data) to predict the future behavior of individuals in order to drive better decisions." In future industrial systems, the value of predictive analytics will be to predict and prevent potential issues to achieve near-zero break-down and further be integrated into prescriptive analytics for decision optimization. Furthermore, the converted data can be used for closed-loop product life cycle improvement which is the vision of the Industrial Internet Consortium.

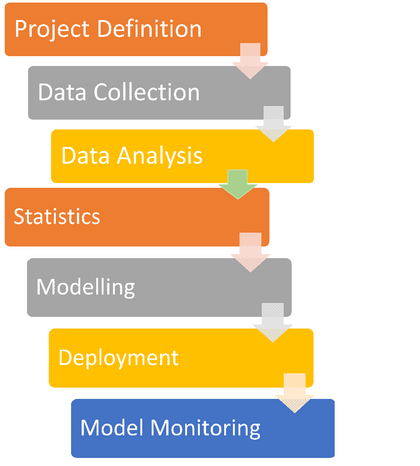
Predictive Analytics Process

Predictive Analytics Process

1. Define Project : Define the project outcomes, deliverable, scope of the effort, business objectives, identify the data sets that are going to be used.
2. Data Collection : Data mining for predictive analytics prepares data from multiple sources for analysis. This provides a complete view of customer interactions.
3. Data Analysis : Data Analysis is the process of inspecting, cleaning and modelling data with the objective of discovering useful information, arriving at conclusion
4. Statistics : Statistical Analysis enables to validate the assumptions, hypothesis and test them using standard statistical models.
5. Modelling : Predictive modelling provides the ability to automatically create accurate predictive models about future. There are also options to choose the best solution with multi-modal evaluation.
6. Deployment : Predictive model deployment provides the option to deploy the analytical results into everyday decision making process to get results, reports and output by automating the decisions based on the modelling.
7. Model Monitoring : Models are managed and monitored to review the model performance to ensure that it is providing the results expected.

Types

Generally, the term predictive analytics is used to mean predictive modeling, "scoring" data with predictive models, and forecasting. However, people are increasingly using the term to refer to related analytical disciplines, such as descriptive modeling and decision modeling or optimization. These disciplines also involve rigorous data analysis, and are widely used in business for segmentation and decision making, but have different purposes and the statistical techniques underlying them vary.

Predictive models

Predictive models are models of the relation between the specific performance of a unit in a sample and one or more known attributes or features of the unit. The objective of the model is to assess the likelihood that a similar unit in a different sample will exhibit the specific performance. This category encompasses models in many areas, such as marketing, where they seek out subtle data patterns to answer questions about customer performance, or fraud detection models. Predictive models often perform calculations during live transactions, for example, to evaluate the risk or opportunity of a given customer or transaction, in order to guide a decision. With advancements in computing speed, individual agent modeling systems have become capable of simulating human behaviour or reactions to given stimuli or scenarios.

The available sample units with known attributes and known performances is referred to as the "training sample". The units in other samples, with known attributes but unknown performances, are referred to as "out of [training] sample" units. The out of sample units do not necessarily bear a chronological relation to the training sample units. For example, the training sample may consist of literary attributes of writings by Victorian authors, with known attribution, and the out-of sample unit may be newly found writing with unknown authorship; a predictive model may aid in attributing a work to a known author. Another example is given by analysis of blood splatter in simulated crime scenes in which the out of sample unit is the actual blood splatter pattern from a crime scene. The out of sample unit may be from the same time as the training units, from a previous time, or from a future time.

Descriptive models

Descriptive models quantify relationships in data in a way that is often used to classify customers or prospects into groups. Unlike predictive models that focus on predicting a single customer behavior (such as credit risk), descriptive models identify many different relationships between customers or products. Descriptive models do not rank-order customers by their likelihood of taking a particular action the way predictive models do. Instead, descriptive models can be used, for example, to categorize customers by their product preferences and life stage. Descriptive modeling tools can be utilized to develop further models that can simulate large number of individualized agents and make predictions.

Decision models

Decision models describe the relationship between all the elements of a decision—the known data (including results of predictive models), the decision, and the forecast results of the decision—in order to predict the results of decisions involving many variables. These models can be used in optimization, maximizing certain outcomes while minimizing others. Decision models are generally used to develop decision logic or a set of business rules that will produce the desired action for every customer or circumstance.

Applications

Although predictive analytics can be put to use in many applications, we outline a few examples where predictive analytics has shown positive impact in recent years.

Analytical customer relationship management (CRM)

Analytical customer relationship management (CRM) is a frequent commercial application of predictive analysis. Methods of predictive analysis are applied to customer data to pursue CRM objectives, which involve constructing a holistic view of the customer no matter where their information resides in the company or the department involved. CRM uses predictive analysis in applications for marketing campaigns, sales, and customer services to name a few. These tools are required in order for a company to posture and focus their efforts effectively across the breadth of their customer base. They must analyze and understand the products in demand or have the potential for high demand, predict customers' buying habits in order to promote relevant products at multiple touch points, and proactively identify and mitigate issues that have the potential to lose customers or reduce their ability to gain new ones. Analytical customer relationship management can be applied throughout the customers' lifecycle (acquisition, relationship growth, retention, and win-back). Several of the application areas described below (direct marketing, cross-sell, customer retention) are part of customer relationship management.

Child protection

Over the last 5 years, some child welfare agencies have started using predictive analytics to flag high risk cases. The approach has been called "innovative" by the Commission to Eliminate Child Abuse and Neglect Fatalities (CECANF), and in Hillsborough County, Florida, where the lead child welfare agency uses a predictive modeling tool, there have been no abuse-related child deaths in the target population as of this writing.

Clinical decision support systems

Experts use predictive analysis in health care primarily to determine which patients are at risk of developing certain conditions, like diabetes, asthma, heart disease, and other lifetime illnesses. Additionally, sophisticated clinical decision support systems incorporate predictive analytics to support medical decision making at the point of care. A working definition has been proposed by Jerome A. Osheroff and colleagues:

Clinical decision support (CDS) provides clinicians, staff, patients, or other individuals with knowledge and person-specific information, intelligently filtered or presented at appropriate times, to enhance health and health care. It encompasses a variety of tools and interventions such as computerized alerts and reminders, clinical guidelines, order sets, patient data reports and dashboards, documentation templates, diagnostic support, and clinical workflow tools.

A 2016 study of neurodegenerative disorders provides a powerful example of a CDS platform to diagnose, track, predict and monitor the progression of Parkinson's disease. Using large and multi-source imaging, genetics, clinical and demographic data, these investigators developed a decision support system that can predict the state of the disease with high accuracy, consistency and precision. They employed classical model-based and machine learning model-free methods to discriminate between different patient and control groups. Similar approaches may be used for predictive diagnosis and disease progression forecasting in many neurodegenerative disorders like Alzheimer’s, Huntington’s, Amyotrophic Lateral Sclerosis, as well as for other clinical and biomedical applications where Big Data is available.

Collection analytics

Many portfolios have a set of delinquent customers who do not make their payments on time. The financial institution has to undertake collection activities on these customers to recover the amounts due. A lot of collection resources are wasted on customers who are difficult or impossible to recover. Predictive analytics can help optimize the allocation of collection resources by identifying the most effective collection agencies, contact strategies, legal actions and other strategies to each customer, thus significantly increasing recovery at the same time reducing collection costs.

Cross-sell

Often corporate organizations collect and maintain abundant data (e.g. customer records, sale transactions) as exploiting hidden relationships in the data can provide a competitive advantage. For an organization that offers multiple products, predictive analytics can help analyze customers' spending, usage and other behavior, leading to efficient cross sales, or selling additional products to current customers. This directly leads to higher profitability per customer and stronger customer relationships.

Customer retention

With the number of competing services available, businesses need to focus efforts on maintaining continuous customer satisfaction, rewarding consumer loyalty and minimizing customer attrition. In addition, small increases in customer retention have been shown to increase profits disproportionately. One study concluded that a 5% increase in customer retention rates will increase profits by 25% to 95%. Businesses tend to respond to customer attrition on a reactive basis, acting only after the customer has initiated the process to terminate service. At this stage, the chance of changing the customer's decision is almost zero. Proper application of predictive analytics can lead to a more proactive retention strategy. By a frequent examination of a customer's past service usage, service performance, spending and other behavior patterns, predictive models can determine the likelihood of a customer terminating service sometime soon. An intervention with lucrative offers can increase the chance of retaining the customer. Silent attrition, the behavior of a customer to slowly but steadily reduce usage, is another problem that many companies face. Predictive analytics can also predict this behavior, so that the company can take proper actions to increase customer activity.

Direct marketing

When marketing consumer products and services, there is the challenge of keeping up with competing products and consumer behavior. Apart from identifying prospects, predictive analytics can also help to identify the most effective combination of product versions, marketing material, communication channels and timing that should be used to target a given consumer. The goal of predictive analytics is typically to lower the cost per order or cost per action.

Fraud detection

Fraud is a big problem for many businesses and can be of various types: inaccurate credit applications, fraudulent transactions (both offline and online), identity thefts and false insurance claims. Some examples of likely victims are credit card issuers, insurance companies, retail merchants, manufacturers, business-to-business suppliers and even services providers. A predictive model can help weed out the "bads" and reduce a business's exposure to fraud.

Predictive modeling can also be used to identify high-risk fraud candidates in business or the public sector. Mark Nigrini developed a risk-scoring method to identify audit targets. He describes the use of this approach to detect fraud in the franchisee sales reports of an international fast-food chain. Each location is scored using 10 predictors. The 10 scores are then weighted to give one final overall risk score for each location. The same scoring approach was also used to identify high-risk check kiting accounts, potentially fraudulent travel agents, and questionable vendors. A reasonably complex model was used to identify fraudulent monthly reports submitted by divisional controllers.

The Internal Revenue Service (IRS) of the United States also uses predictive analytics to mine tax returns and identify tax fraud.

Recent advancements in technology have also introduced predictive behavior analysis for web fraud detection. This type of solution utilizes heuristics in order to study normal web user behavior and detect anomalies indicating fraud attempts.

Portfolio, product or economy-level prediction

Often the focus of analysis is not the consumer but the product, portfolio, firm, industry or even the economy. For example, a retailer might be interested in predicting store-level demand for inventory management purposes. Or the Federal Reserve Board might be interested in predicting the unemployment rate for the next year. These types of problems can be addressed by predictive analytics using time series techniques (see below). They can also be addressed via machine learning approaches which transform the original time series into a feature vector space, where the learning algorithm finds patterns that have predictive power.

Project risk management

When employing risk management techniques, the results are always to predict and benefit from a future scenario. The capital asset pricing model (CAP-M) "predicts" the best portfolio to maximize return. Probabilistic risk assessment (PRA) when combined with mini-Delphi techniques and statistical approaches yields accurate forecasts. These are examples of approaches that can extend from project to market, and from near to long term. Underwriting (see below) and other business approaches identify risk management as a predictive method.

Underwriting

Many businesses have to account for risk exposure due to their different services and determine the cost needed to cover the risk. For example, auto insurance providers need to accurately determine the amount of premium to charge to cover each automobile and driver. A financial company needs to assess a borrower's potential and ability to pay before granting a loan. For a health insurance provider, predictive analytics can analyze a few years of past medical claims data, as well as lab, pharmacy and other records where available, to predict how expensive an enrollee is likely to be in the future. Predictive analytics can help underwrite these quantities by predicting the chances of illness, default, bankruptcy, etc. Predictive analytics can streamline the process of customer acquisition by predicting the future risk behavior of a customer using application level data. Predictive analytics in the form of credit scores have reduced the amount of time it takes for loan approvals, especially in the mortgage market where lending decisions are now made in a matter of hours rather than days or even weeks. Proper predictive analytics can lead to proper pricing decisions, which can help mitigate future risk of default.

Technology and big data influences

Big data is a collection of data sets that are so large and complex that they become awkward to work with using traditional database management tools. The volume, variety and velocity of big data have introduced challenges across the board for capture, storage, search, sharing, analysis, and visualization. Examples of big data sources include web logs, RFID, sensor data, social networks, Internet search indexing, call detail records, military surveillance, and complex data in astronomic, biogeochemical, genomics, and atmospheric sciences. Big Data is the core of most predictive analytic services offered by IT organizations. Thanks to technological advances in computer hardware—faster CPUs, cheaper memory, and MPP architectures—and new technologies such as Hadoop, MapReduce, and in-database and text analytics for processing big data, it is now feasible to collect, analyze, and mine massive amounts of structured and unstructured data for new insights. It is also possible to run predictive algorithms on streaming data. Today, exploring big data and using predictive analytics is within reach of more organizations than ever before and new methods that are capable for handling such datasets are proposed.

Analytical techniques

The approaches and techniques used to conduct predictive analytics can broadly be grouped into regression techniques and machine learning techniques.

Regression techniques

Regression models are the mainstay of predictive analytics. The focus lies on establishing a mathematical equation as a model to represent the interactions between the different variables in consideration. Depending on the situation, there are a wide variety of models that can be applied while performing predictive analytics. Some of them are briefly discussed below.

Linear regression model

The linear regression model analyzes the relationship between the response or dependent variable and a set of independent or predictor variables. This relationship is expressed as an equation that predicts the response variable as a linear function of the parameters. These parameters are adjusted so that a measure of fit is optimized. Much of the effort in model fitting is focused on minimizing the size of the residual, as well as ensuring that it is randomly distributed with respect to the model predictions.

The goal of regression is to select the parameters of the model so as to minimize the sum of the squared residuals. This is referred to as ordinary least squares (OLS) estimation and results in best linear unbiased estimates (BLUE) of the parameters if and only if the Gauss-Markov assumptions are satisfied.

Once the model has been estimated we would be interested to know if the predictor variables belong in the model—i.e. is the estimate of each variable's contribution reliable? To do this we can check the statistical significance of the model's coefficients which can be measured using the t-statistic. This amounts to testing whether the coefficient is significantly different from zero. How well the model predicts the dependent variable based on the value of the independent variables can be assessed by using the R² statistic. It measures predictive power of the model i.e. the proportion of the total variation in the dependent variable that is "explained" (accounted for) by variation in the independent variables.

Discrete choice models

Multiple regression (above) is generally used when the response variable is continuous and has an unbounded range. Often the response variable may not be continuous but rather discrete. While mathematically it is feasible to apply multiple regression to discrete ordered dependent variables, some of the assumptions behind the theory of multiple linear regression no longer hold, and there are other techniques such as discrete choice models which are better suited for this type of analysis. If the dependent variable is discrete, some of those superior methods are logistic regression, multinomial logit and probit models. Logistic regression and probit models are used when the dependent variable is binary.

Logistic regression

In a classification setting, assigning outcome probabilities to observations can be achieved through the use of a logistic model, which is basically a method which transforms information about the binary dependent variable into an unbounded continuous variable and estimates a regular multivariate model (See Allison's Logistic Regression for more information on the theory of logistic regression).
The Wald and likelihood-ratio test are used to test the statistical significance of each coefficient b in the model (analogous to the t tests used in OLS regression; see above). A test assessing the goodness-of-fit of a classification model is the "percentage correctly predicted".

Multinomial logistic regression

An extension of the binary logit model to cases where the dependent variable has more than 2 categories is the multinomial logit model. In such cases collapsing the data into two categories might not make good sense or may lead to loss in the richness of the data. The multinomial logit model is the appropriate technique in these cases, especially when the dependent variable categories are not ordered (for examples colors like red, blue, green). Some authors have extended multinomial regression to include feature selection/importance methods such as random multinomial logit.

Probit regression

Probit models offer an alternative to logistic regression for modeling categorical dependent variables. Even though the outcomes tend to be similar, the underlying distributions are different. Probit models are popular in social sciences like economics.

A good way to understand the key difference between probit and logit models is to assume that the dependent variable is driven by a latent variable z, which is a sum of a linear combination of explanatory variables and a random noise term.

We do not observe z but instead observe y which takes the value 0 (when z < 0) or 1 (otherwise). In the logit model we assume that the random noise term follows a logistic distribution with mean zero. In the probit model we assume that it follows a normal distribution with mean zero. Note that in social sciences (e.g. economics), probit is often used to model situations where the observed variable y is continuous but takes values between 0 and 1.

Logit versus probit

The probit model has been around longer than the logit model. They behave similarly, except that the logistic distribution tends to be slightly flatter tailed. One of the reasons the logit model was formulated was that the probit model was computationally difficult due to the requirement of numerically calculating integrals. Modern computing however has made this computation fairly simple. The coefficients obtained from the logit and probit model are fairly close. However, the odds ratio is easier to interpret in the logit model.

Practical reasons for choosing the probit model over the logistic model would be:

• There is a strong belief that the underlying distribution is normal
• The actual event is not a binary outcome (e.g., bankruptcy status) but a proportion (e.g., proportion of population at different debt levels).

Time series models

Time series models are used for predicting or forecasting the future behavior of variables. These models account for the fact that data points taken over time may have an internal structure (such as autocorrelation, trend or seasonal variation) that should be accounted for. As a result, standard regression techniques cannot be applied to time series data and methodology has been developed to decompose the trend, seasonal and cyclical component of the series. Modeling the dynamic path of a variable can improve forecasts since the predictable component of the series can be projected into the future.

Time series models estimate difference equations containing stochastic components. Two commonly used forms of these models are autoregressive models (AR) and moving-average (MA) models. The Box–Jenkins methodology (1976) developed by George Box and G.M. Jenkins combines the AR and MA models to produce the ARMA (autoregressive moving average) model, which is the cornerstone of stationary time series analysis. ARIMA (autoregressive integrated moving average models), on the other hand, are used to describe non-stationary time series. Box and Jenkins suggest differencing a non-stationary time series to obtain a stationary series to which an ARMA model can be applied. Non-stationary time series have a pronounced trend and do not have a constant long-run mean or variance.

Box and Jenkins proposed a three-stage methodology involving model identification, estimation and validation. The identification stage involves identifying if the series is stationary or not and the presence of seasonality by examining plots of the series, autocorrelation and partial autocorrelation functions. In the estimation stage, models are estimated using non-linear time series or maximum likelihood estimation procedures. Finally the validation stage involves diagnostic checking such as plotting the residuals to detect outliers and evidence of model fit.

In recent years time series models have become more sophisticated and attempt to model conditional heteroskedasticity with models such as ARCH (autoregressive conditional heteroskedasticity) and GARCH (generalized autoregressive conditional heteroskedasticity) models frequently used for financial time series. In addition time series models are also used to understand inter-relationships among economic variables represented by systems of equations using VAR (vector autoregression) and structural VAR models.

Survival or duration analysis

Survival analysis is another name for time-to-event analysis. These techniques were primarily developed in the medical and biological sciences, but they are also widely used in the social sciences like economics, as well as in engineering (reliability and failure time analysis).

Censoring and non-normality, which are characteristic of survival data, generate difficulty when trying to analyze the data using conventional statistical models such as multiple linear regression. The normal distribution, being a symmetric distribution, takes positive as well as negative values, but duration by its very nature cannot be negative and therefore normality cannot be assumed when dealing with duration/survival data. Hence the normality assumption of regression models is violated.

The assumption is that if the data were not censored it would be representative of the population of interest. In survival analysis, censored observations arise whenever the dependent variable of interest represents the time to a terminal event, and the duration of the study is limited in time.

An important concept in survival analysis is the hazard rate, defined as the probability that the event will occur at time t conditional on surviving until time t. Another concept related to the hazard rate is the survival function which can be defined as the probability of surviving to time t.

Most models try to model the hazard rate by choosing the underlying distribution depending on the shape of the hazard function. A distribution whose hazard function slopes upward is said to have positive duration dependence, a decreasing hazard shows negative duration dependence whereas constant hazard is a process with no memory usually characterized by the exponential distribution. Some of the distributional choices in survival models are: F, gamma, Weibull, log normal, inverse normal, exponential etc. All these distributions are for a non-negative random variable.

Duration models can be parametric, non-parametric or semi-parametric. Some of the models commonly used are Kaplan-Meier and Cox proportional hazard model (non parametric).

Classification and regression trees (CART)

Globally-optimal classification tree analysis (GO-CTA) (also called hierarchical optimal discriminant analysis) is a generalization of optimal discriminant analysis that may be used to identify the statistical model that has maximum accuracy for predicting the value of a categorical dependent variable for a dataset consisting of categorical and continuous variables. The output of HODA is a non-orthogonal tree that combines categorical variables and cut points for continuous variables that yields maximum predictive accuracy, an assessment of the exact Type I error rate, and an evaluation of potential cross-generalizability of the statistical model. Hierarchical optimal discriminant analysis may be thought of as a generalization of Fisher's linear discriminant analysis. Optimal discriminant analysis is an alternative to ANOVA (analysis of variance) and regression analysis, which attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA and regression analysis give a dependent variable that is a numerical variable, while hierarchical optimal discriminant analysis gives a dependent variable that is a class variable.
Classification and regression trees (CART) are a non-parametric decision tree learning technique that produces either classification or regression trees, depending on whether the dependent variable is categorical or numeric, respectively.

Decision trees are formed by a collection of rules based on variables in the modeling data set:

• Rules based on variables' values are selected to get the best split to differentiate observations based on the dependent variable
• Once a rule is selected and splits a node into two, the same process is applied to each "child" node (i.e. it is a recursive procedure)
• Splitting stops when CART detects no further gain can be made, or some pre-set stopping rules are met. (Alternatively, the data are split as much as possible and then the tree is later pruned.)

Each branch of the tree ends in a terminal node. Each observation falls into one and exactly one terminal node, and each terminal node is uniquely defined by a set of rules.
A very popular method for predictive analytics is Leo Breiman's random forests.

Multivariate adaptive regression splines

Multivariate adaptive regression splines (MARS) is a non-parametric technique that builds flexible models by fitting piecewise linear regressions.

An important concept associated with regression splines is that of a knot. Knot is where one local regression model gives way to another and thus is the point of intersection between two splines.

In multivariate and adaptive regression splines, basis functions are the tool used for generalizing the search for knots. Basis functions are a set of functions used to represent the information contained in one or more variables. Multivariate and Adaptive Regression Splines model almost always creates the basis functions in pairs.

Multivariate and adaptive regression spline approach deliberately overfits the model and then prunes to get to the optimal model. The algorithm is computationally very intensive and in practice we are required to specify an upper limit on the number of basis functions.

Machine learning techniques

Machine learning, a branch of artificial intelligence, was originally employed to develop techniques to enable computers to learn. Today, since it includes a number of advanced statistical methods for regression and classification, it finds application in a wide variety of fields including medical diagnostics, credit card fraud detection, face and speech recognition and analysis of the stock market. In certain applications it is sufficient to directly predict the dependent variable without focusing on the underlying relationships between variables. In other cases, the underlying relationships can be very complex and the mathematical form of the dependencies unknown. For such cases, machine learning techniques emulate human cognition and learn from training examples to predict future events.

A brief discussion of some of these methods used commonly for predictive analytics is provided below. A detailed study of machine learning can be found in Mitchell (1997).

Neural networks

Neural networks are nonlinear sophisticated modeling techniques that are able to model complex functions. They can be applied to problems of prediction, classification or control in a wide spectrum of fields such as finance, cognitive psychology/neuroscience, medicine, engineering, and physics.

Neural networks are used when the exact nature of the relationship between inputs and output is not known. A key feature of neural networks is that they learn the relationship between inputs and output through training. There are three types of training used by different neural networks: supervised and unsupervised training and reinforcement learning, with supervised being the most common one.

Some examples of neural network training techniques are backpropagation, quick propagation, conjugate gradient descent, projection operator, Delta-Bar-Delta etc. Some unsupervised network architectures are multilayer perceptrons, Kohonen networks, Hopfield networks, etc.

Multilayer perceptron (MLP)

The multilayer perceptron (MLP) consists of an input and an output layer with one or more hidden layers of nonlinearly-activating nodes or sigmoid nodes. This is determined by the weight vector and it is necessary to adjust the weights of the network. The backpropagation employs gradient fall to minimize the squared error between the network output values and desired values for those outputs. The weights adjusted by an iterative process of repetitive present of attributes. Small changes in the weight to get the desired values are done by the process called training the net and is done by the training set (learning rule).

Radial basis functions

A radial basis function (RBF) is a function which has built into it a distance criterion with respect to a center. Such functions can be used very efficiently for interpolation and for smoothing of data. Radial basis functions have been applied in the area of neural networks where they are used as a replacement for the sigmoidal transfer function. Such networks have 3 layers, the input layer, the hidden layer with the RBF non-linearity and a linear output layer. The most popular choice for the non-linearity is the Gaussian. RBF networks have the advantage of not being locked into local minima as do the feed-forward networks such as the multilayer perceptron.

Support vector machines

Support vector machines (SVM) are used to detect and exploit complex patterns in data by clustering, classifying and ranking the data. They are learning machines that are used to perform binary classifications and regression estimations. They commonly use kernel based methods to apply linear classification techniques to non-linear classification problems. There are a number of types of SVM such as linear, polynomial, sigmoid etc.

Naïve Bayes

Naïve Bayes based on Bayes conditional probability rule is used for performing classification tasks. Naïve Bayes assumes the predictors are statistically independent which makes it an effective classification tool that is easy to interpret. It is best employed when faced with the "curse of dimensionality" problem, i.e. when the number of predictors is very high.

k-nearest neighbours

The nearest neighbour algorithm (KNN) belongs to the class of pattern recognition statistical methods. The method does not impose a priori any assumptions about the distribution from which the modeling sample is drawn. It involves a training set with both positive and negative values. A new sample is classified by calculating the distance to the nearest neighbouring training case. The sign of that point will determine the classification of the sample. In the k-nearest neighbour classifier, the k nearest points are considered and the sign of the majority is used to classify the sample. The performance of the kNN algorithm is influenced by three main factors: (1) the distance measure used to locate the nearest neighbours, (2) the decision rule used to derive a classification from the k-nearest neighbours, and (3) the number of neighbours used to classify the new sample. It can be proved that, unlike other methods, this method is universally asymptotically convergent, i.e. as the size of the training set increases, if the observations are independent and identically distributed (i.i.d.), regardless of the distribution from which the sample is drawn, the predicted class will converge to the class assignment that minimizes misclassification error. See Devroy et al.

Geospatial predictive modeling

Conceptually, geospatial predictive modeling is rooted in the principle that the occurrences of events being modeled are limited in distribution. Occurrences of events are neither uniform nor random in distribution—there are spatial environment factors (infrastructure, sociocultural, topographic, etc.) that constrain and influence where the locations of events occur. Geospatial predictive modeling attempts to describe those constraints and influences by spatially correlating occurrences of historical geospatial locations with environmental factors that represent those constraints and influences. Geospatial predictive modeling is a process for analyzing events through a geographic filter in order to make statements of likelihood for event occurrence or emergence.

Tools

Historically, using predictive analytics tools—as well as understanding the results they delivered—required advanced skills. However, modern predictive analytics tools are no longer restricted to IT specialists.^{[citation needed]} As more organizations adopt predictive analytics into decision-making processes and integrate it into their operations, they are creating a shift in the market toward business users as the primary consumers of the information. Business users want tools they can use on their own. Vendors are responding by creating new software that removes the mathematical complexity, provides user-friendly graphic interfaces and/or builds in short cuts that can, for example, recognize the kind of data available and suggest an appropriate predictive model. Predictive analytics tools have become sophisticated enough to adequately present and dissect data problems, so that any data-savvy information worker can utilize them to analyze data and retrieve meaningful, useful results. For example, modern tools present findings using simple charts, graphs, and scores that indicate the likelihood of possible outcomes.

There are numerous tools available in the marketplace that help with the execution of predictive analytics. These range from those that need very little user sophistication to those that are designed for the expert practitioner. The difference between these tools is often in the level of customization and heavy data lifting allowed.

Some open-source software predictive analytic tools include:

• Apache Mahout
• GNU Octave
• KNIME
• OpenNN
• Orange
• R
• scikit-learn (Python)
• Weka

Commercial predictive analytic tools include:

• Alpine Data Labs
• Alteryx
• Angoss KnowledgeSTUDIO
• Actuate Corporation BIRT Analytics
• IBM SPSS Statistics and IBM SPSS Modeler
• KXEN Inc. Modeler
• Mathematica
• MATLAB
• Minitab
• LabVIEW
• Neural Designer
• Oracle Advanced Analytics
• Pervasive
• Predixion Software
• Presenso
• RapidMiner
• RCASE
• Revolution Analytics
• SAP HANA and SAP BusinessObjects Predictive Analytics
• SAS and its Enterprise Miner
• Sidetrade
• Stata
• Statgraphics
• Statistica
• Tibco Software

Beside these software packages, specific tools have also been developed for industrial applications. For example, Watchdog Agent Toolbox has been developed and optimized for predictive analysis in prognostics and health management applications and is available for MATLAB and LabVIEW.

The most popular commercial predictive analytics software packages according to the Rexer Analytics Survey for 2013 are IBM SPSS Modeler, SAS Enterprise Miner, and Dell Statistica.

PMML

The Predictive Model Markup Language (PMML) was proposed for standard language for expressing predictive models. Such an XML-based language provides a way for the different tools to define predictive models and to share them. PMML 4.0 was released in June, 2009.

Criticism

There are plenty of skeptics when it comes to computers' and algorithms' abilities to predict the future, including Gary King, a professor from Harvard University and the director of the Institute for Quantitative Social Science. People are influenced by their environment in innumerable ways. Predicting perfectly what people will do next requires that all the influential variables be known and measured accurately. "People's environments change even more quickly than they themselves do. Everything from the weather to their relationship with their mother can change the way people think and act. All of those variables are unpredictable. How they will impact a person is even less predictable. If put in the exact same situation tomorrow, they may make a completely different decision. This means that a statistical prediction is only valid in sterile laboratory conditions, which suddenly isn't as useful as it seemed before."
In a study of 1072 papers published in Information Systems Research and MIS Quarterly between 1990 and 2006, only 52 empirical papers attempted predictive claims, of which only 7 carried out proper predictive modeling or testing.^[44]

Siméon Denis Poisson

From Wikipedia, the free encyclopedia

Siméon Poisson
Siméon Denis Poisson (1781–1840)
Born	21 June 1781 Pithiviers, Orléanais, Kingdom of France (present-day Loiret, France)
Died	25 April 1840 (aged 58) Sceaux, Hauts-de-Seine, July Monarchy
Nationality	French
Alma mater	École Polytechnique
Known for	Poisson process Poisson equation Poisson kernel Poisson distribution Poisson bracket Poisson algebra Poisson regression Poisson summation formula Poisson's spot Poisson's ratio Poisson zeros Conway–Maxwell–Poisson distribution Euler–Poisson–Darboux equation
Scientific career
Fields	Mathematics
Institutions	École Polytechnique Bureau des Longitudes Faculté des sciences de Paris (fr) École de Saint-Cyr
Academic advisors	Joseph-Louis Lagrange Pierre-Simon Laplace
Doctoral students	Michel Chasles Joseph Liouville
Other notable students	Nicolas Léonard Sadi Carnot Peter Gustav Lejeune Dirichlet

Baron Siméon Denis Poisson FRS FRSE (French: [si.me.ɔ̃ də.ni pwa.sɔ̃]; 21 June 1781 – 25 April 1840) was a French mathematician, engineer, and physicist, who made several scientific advances.
Within the elite Académie des Sciences he was a leading opponent of the wave theory of light, eventually being proven wrong by Augustin-Jean Fresnel.

Biography

Poisson was born in Pithiviers, Loiret district in France, the son of Siméon Poisson, an officer in the French army.

In 1798, he entered the École Polytechnique in Paris as first in his year, and immediately began to attract the notice of the professors of the school, who left him free to make his own decisions as to what he would study. In 1800, less than two years after his entry, he published two memoirs, one on Étienne Bézout's method of elimination, the other on the number of integrals of a finite difference equation. The latter was examined by Sylvestre-François Lacroix and Adrien-Marie Legendre, who recommended that it should be published in the Recueil des savants étrangers, an unprecedented honor for a youth of eighteen. This success at once procured entry for Poisson into scientific circles.  Joseph Louis Lagrange, whose lectures on the theory of functions he attended at the École Polytechnique, recognized his talent early on, and became his friend (the Mathematics Genealogy Project lists Lagrange as his advisor, but this may be an approximation); while Pierre-Simon Laplace, in whose footsteps Poisson followed, regarded him almost as his son. The rest of his career, till his death in Sceaux near Paris, was nearly occupied by the composition and publication of his many works and in fulfilling the duties of the numerous educational positions to which he was successively appointed.

Immediately after finishing his studies at the École Polytechnique, he was appointed répétiteur (teaching assistant) there, a position which he had occupied as an amateur while still a pupil in the school; for his schoolmates had made a custom of visiting him in his room after an unusually difficult lecture to hear him repeat and explain it. He was made deputy professor (professeur suppléant) in 1802, and, in 1806 full professor succeeding Jean Baptiste Joseph Fourier, whom Napoleon had sent to Grenoble. In 1808 he became astronomer to the Bureau des Longitudes; and when the Faculté des sciences de Paris (fr) was instituted in 1809 he was appointed a professor of rational mechanics (professeur de mécanique rationelle). He went on to become a member of the Institute in 1812, examiner at the military school (École Militaire) at Saint-Cyr in 1815, graduation examiner at the École Polytechnique in 1816, councillor of the university in 1820, and geometer to the Bureau des Longitudes succeeding Pierre-Simon Laplace in 1827.

In 1817, he married Nancy de Bardi and with her, he had four children. His father, whose early experiences had led him to hate aristocrats, bred him in the stern creed of the First Republic. Throughout the Revolution, the Empire, and the following restoration, Poisson was not interested in politics, concentrating on mathematics. He was appointed to the dignity of baron in 1821; but he neither took out the diploma nor used the title. In March 1818, he was elected a Fellow of the Royal Society, in 1822 a Foreign Honorary Member of the American Academy of Arts and Sciences, and in 1823 a foreign member of the Royal Swedish Academy of Sciences. The revolution of July 1830 threatened him with the loss of all his honours; but this disgrace to the government of Louis-Philippe was adroitly averted by François Jean Dominique Arago, who, while his "revocation" was being plotted by the council of ministers, procured him an invitation to dine at the Palais-Royal, where he was openly and effusively received by the citizen king, who "remembered" him. After this, of course, his degradation was impossible, and seven years later he was made a peer of France, not for political reasons, but as a representative of French science.

As a teacher of mathematics Poisson is said to have been extraordinarily successful, as might have been expected from his early promise as a répétiteur at the École Polytechnique. As a scientific worker, his productivity has rarely if ever been equaled. Notwithstanding his many official duties, he found time to publish more than three hundred works, several of them extensive treatises, and many of them memoirs dealing with the most abstruse branches of pure mathematics, applied mathematics, mathematical physics, and rational mechanics. (Arago attributed to him the quote, "Life is good for only two things: doing mathematics and teaching it.")

A list of Poisson's works, drawn up by himself, is given at the end of Arago's biography. All that is possible is a brief mention of the more important ones. It was in the application of mathematics to physics that his greatest services to science were performed. Perhaps the most original, and certainly the most permanent in their influence, were his memoirs on the theory of electricity and magnetism, which virtually created a new branch of mathematical physics.

Next (or in the opinion of some, first) in importance stand the memoirs on celestial mechanics, in which he proved himself a worthy successor to Pierre-Simon Laplace. The most important of these are his memoirs Sur les inégalités séculaires des moyens mouvements des planètes, Sur la variation des constantes arbitraires dans les questions de mécanique, both published in the Journal of the École Polytechnique (1809); Sur la libration de la lune, in Connaissance des temps (1821), etc.; and Sur le mouvement de la terre autour de son centre de gravité, in Mémoires de l'Académie (1827), etc. In the first of these memoirs, Poisson discusses the famous question of the stability of the planetary orbits, which had already been settled by Lagrange to the first degree of approximation for the disturbing forces. Poisson showed that the result could be extended to a second approximation, and thus made an important advance in planetary theory. The memoir is remarkable inasmuch as it roused Lagrange, after an interval of inactivity, to compose in his old age one of the greatest of his memoirs, entitled Sur la théorie des variations des éléments des planètes, et en particulier des variations des grands axes de leurs orbites. So highly did he think of Poisson's memoir that he made a copy of it with his own hand, which was found among his papers after his death. Poisson made important contributions to the theory of attraction.

His name is one of the 72 names inscribed on the Eiffel Tower.

Contributions

Mémoire sur le calcul numerique des integrales définies, 1826

Poisson's well-known generalization of Laplace's second order partial differential equation for potential:

${\displaystyle \nabla ^{2}\phi =-4\pi \rho \;}$

today named after him Poisson's equation or the potential theory equation, was first published in the Bulletin de la société philomatique (1813). If ρ = 0, we get Laplace's equation:

${\displaystyle \nabla ^{2}\phi =0\;.}$

In 1812, Poisson discovered that Laplace's equation is valid only outside of a solid. A rigorous proof for masses with variable density was first given by Carl Friedrich Gauss in 1839. Both equations have their equivalents in vector algebra. Poisson's equation for the divergence of the gradient of a scalar field, φ in 3-dimensional space is:

${\displaystyle \nabla ^{2}\phi =\rho (x,y,z)\;.}$

Consider for instance Poisson's equation for surface electrical potential, Ψ as a function of the density of electric charge, ρ_e at a particular point:

${\displaystyle \nabla ^{2}\Psi ={\partial ^{2}\Psi \over \partial x^{2}}+{\partial ^{2}\Psi \over \partial y^{2}}+{\partial ^{2}\Psi \over \partial z^{2}}=-{\rho _{e} \over \varepsilon \varepsilon _{0}}\;.}$

The distribution of a charge in a fluid is unknown and we have to use the Poisson–Boltzmann equation:

${\displaystyle \nabla ^{2}\Psi ={n_{0}e \over \varepsilon \varepsilon _{0}}\left(e^{e\Psi (x,y,z)/k_{B}T}-e^{-e\Psi (x,y,z)/k_{B}T}\right),\;}$

which in most cases cannot be solved analytically. In polar coordinates the Poisson–Boltzmann equation is:

${\displaystyle {1 \over r^{2}}{d \over dr}\left(r^{2}{d\Psi \over dr}\right)={n_{0}e \over \varepsilon \varepsilon _{0}}\left(e^{e\Psi (r)/k_{B}T}-e^{-e\Psi (r)/k_{B}T}\right)\;}$

which also cannot be solved analytically. If a field, φ is not scalar, the Poisson equation is valid, as can be for example in 4-dimensional Minkowski space:

${\displaystyle {\sqrt {\phi _{ik}}}=\rho (x,y,z,ct)\;.}$

If ρ(x, y, z) is a continuous function and if for r→ ∞ (or if a point 'moves' to infinity) a function φ goes to 0 fast enough, a solution of Poisson's equation is the Newtonian potential of a function ρ(x, y, z):

${\displaystyle \phi _{M}=-{1 \over 4\pi }\int {\rho (x,y,z)\,dv \over r}\;}$

where r is a distance between a volume element dv and a point M. The integration runs over the whole space.

Another "Poisson's integral" is the solution for the Green function for Laplace's equation with Dirichlet condition over a circular disk:

${\displaystyle \phi (\xi \eta )={1 \over 4\pi }\int _{0}^{2\pi }{R^{2}-\rho ^{2} \over R^{2}+\rho ^{2}-2R\rho \cos(\psi -\chi )}\phi (\chi )\,d\chi \;}$

where

${\displaystyle \xi =\rho \cos \psi ,\;}$

${\displaystyle \quad \eta =\rho \sin \psi ,\;}$

φ is a boundary condition holding on the disk's boundary.

In the same manner, we define the Green function for the Laplace equation with Dirichlet condition, ∇² φ = 0 over a sphere of radius R. This time the Green function is:

${\displaystyle G(x,y,z;\xi ,\eta ,\zeta )={1 \over r}-{R \over r_{1}\rho }\;,}$

where

${\displaystyle \rho ={\sqrt {\xi ^{2}+\eta ^{2}+\zeta ^{2}}}}$ is the distance of a point (ξ, η, ζ) from the center of a sphere,

r is the distance between points (x, y, z) and (ξ, η, ζ), and r₁ is the distance between the point (x, y, z) and the point (Rξ/ρ, Rη/ρ, Rζ/ρ), symmetrical to the point (ξ, η, ζ).

Poisson's integral now has a form:

${\displaystyle \phi (\xi ,\eta ,\zeta )={1 \over 4\pi }\iint _{S}{R^{2}-\rho ^{2} \over Rr^{3}}\phi \,ds\;.}$

Poisson's two most important memoirs on the subject are Sur l'attraction des sphéroides (Connaiss. ft. temps, 1829), and Sur l'attraction d'un ellipsoide homogène (Mim. ft. l'acad., 1835). In concluding our selection from his physical memoirs, we may mention his memoir on the theory of waves (Mém. ft. l'acad., 1825).

In pure mathematics, his most important works were his series of memoirs on definite integrals and his discussion of Fourier series, the latter paving the way for the classic researches of Peter Gustav Lejeune Dirichlet and Bernhard Riemann on the same subject; these are to be found in the Journal of the École Polytechnique from 1813 to 1823, and in the Memoirs de l'Académie for 1823. He also studied Fourier integrals. We may also mention his essay on the calculus of variations (Mem. de l'acad., 1833), and his memoirs on the probability of the mean results of observations (Connaiss. d. temps, 1827, &c). The Poisson distribution in probability theory is named after him.

In his Traité de mécanique (2 vols. 8vo, 1811 and 1833), which was written in the style of Laplace and Lagrange and was long a standard work, he showed many novelties such as an explicit usage of momenta:

${\displaystyle p_{i}={\partial T \over {\partial (\partial q_{i}/\partial t})},}$

which influenced the work of Hamilton and Jacobi.

Besides his many memoirs, Poisson published a number of treatises, most of which were intended to form part of a great work on mathematical physics, which he did not live to complete. Among these may be mentioned:

• Nouvelle théorie de l'action capillaire (4to, 1831);
• Théorie mathématique de la chaleur (4to, 1835);
• Supplement to the same (4to, 1837);
• Recherches sur la probabilité des jugements en matières criminelles et matière civile (4to, 1837), all published at Paris.

A translation of Poisson's Treatise on Mechanics was published in London in 1842.

In 1815 Poisson studied integrations along paths in the complex plane. In 1831 he derived the Navier–Stokes equations independently of Claude-Louis Navier.

Flawed views on the wave theory of light

Poisson showed surprising hubris on the wave theory of light. He was a member of the academic "old guard" at the Académie royale des sciences de l'Institut de France, who were staunch believers in the particle theory of light and were alarmed at the wave theory of light's increasing acceptance. In 1818, the Académie set the topic of their prize as diffraction, being certain that a particle theorist would win it. Poisson, relying on intuition rather than mathematics or scientific experiment, ridiculed participant and civil engineer Augustin-Jean Fresnel when he submitted a thesis explaining diffraction derived from analysis of both the Huygens–Fresnel principle and Young's double slit experiment.

Poisson studied Fresnel's theory in detail and looked for a way to prove it wrong. Poisson thought that he had found a flaw when he demonstrated that Fresnel's theory predicts an on-axis bright spot in the shadow of a circular obstacle blocking a point source of light, where the particle-theory of light predicts complete darkness. Fresnel's theory could not be true, Poisson declared, surely this result was absurd (the Poisson spot is not easily observed in everyday situations, because most everyday sources of light are not good point sources).

The head of the committee, Dominique-François-Jean Arago, who incidentally later became Prime Minister of France, was more open-minded than Poisson and decided to perform the experiment. He molded a 2 mm metallic disk to a glass plate with wax. To everyone's surprise he observed the predicted bright spot, which convinced most scientists of the wave-nature of light. Fresnel won the competition, much to Poisson's chagrin.

After that, the corpuscular theory of light was vanquished, not to be heard of again until in a very different form, the 20^th century revived it as the newly developed wave-particle duality. Arago later noted that the diffraction bright spot (which later became known as both the Arago spot and the Poisson spot) had already been observed by Joseph-Nicolas Delisle and Giacomo F. Maraldi a century earlier.