Lorentz factor

From Wikipedia, the free encyclopedia

 

The Lorentz factor or Lorentz term is the factor by which time, length, and relativistic mass change for an object while that object is moving. The expression appears in several equations in special relativity, and it arises in derivations of the Lorentz transformations. The name originates from its earlier appearance in Lorentzian electrodynamics – named after the Dutch physicist Hendrik Lorentz.

It is generally denoted γ (the Greek lowercase letter gamma). Sometimes (especially in discussion of superluminal motion) the factor is written as Γ (Greek uppercase-gamma) rather than γ.

Definition

The Lorentz factor γ is defined as

${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {dt}{d\tau }}}$,

where:

• v is the relative velocity between inertial reference frames,
• c is the speed of light in a vacuum,
• β is the ratio of v to c,
• t is coordinate time,
• τ is the proper time for an observer (measuring time intervals in the observer's own frame).

This is the most frequently used form in practice, though not the only one (see below for alternative forms). 

To complement the definition, some authors define the reciprocal

${\displaystyle \alpha ={\frac {1}{\gamma }}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\ ={\sqrt {1-{\beta }^{2}}};}$

see velocity addition formula.

Occurrence

Following is a list of formulae from Special relativity which use γ as a shorthand:

• The Lorentz transformation: The simplest case is a boost in the x-direction (more general forms including arbitrary directions and rotations not listed here), which describes how spacetime coordinates change from one inertial frame using coordinates (x, y, z, t) to another (x′, y′, z′, t′) with relative velocity v:

${\displaystyle t'=\gamma \left(t-{\frac {vx}{c^{2}}}\right),}$

${\displaystyle x'=\gamma \left(x-vt\right).}$

Corollaries of the above transformations are the results:

• Time dilation: The time (∆t′) between two ticks as measured in the frame in which the clock is moving, is longer than the time (∆t) between these ticks as measured in the rest frame of the clock:

  ${\displaystyle \Delta t'=\gamma \Delta t.}$

• Length contraction: The length (∆x′) of an object as measured in the frame in which it is moving, is shorter than its length (∆x) in its own rest frame:

  ${\displaystyle \Delta x'=\Delta x/\gamma .}$

Applying conservation of momentum and energy leads to these results:

• Relativistic mass: The mass m of an object in motion is dependent on ${\displaystyle \gamma }$ and the rest mass m₀:

  ${\displaystyle m=\gamma m_{0}.}$

• Relativistic momentum: The relativistic momentum relation takes the same form as for classical momentum, but using the above relativistic mass:

  ${\displaystyle {\vec {p}}=m{\vec {v}}=\gamma m_{0}{\vec {v}}.}$

• Relativistic kinetic energy: The relativistic kinetic energy relation takes the slightly modified form:

• ${\displaystyle E_{k}=E-E_{0}=(\gamma -1)m_{0}c^{2}}$.

Numerical values

Lorentz factor γ as a function of velocity. Its initial value is 1 (when v = 0); and as velocity approaches the speed of light (v → c) γ increases without bound (γ → ∞).

 

α (Lorentz factor inverse) as a function of velocity - a circular arc.

 

In the table below, the left-hand column shows speeds as different fractions of the speed of light (i.e. in units of c). The middle column shows the corresponding Lorentz factor, the final is the reciprocal. Values in bold are exact. 

Speed (units of c)	Lorentz factor	Reciprocal
${\displaystyle \beta =v/c}$	${\displaystyle \gamma }$	${\displaystyle 1/\gamma }$
0.000	1.000	1.000
0.050	1.001	0.999
0.100	1.005	0.995
0.150	1.011	0.989
0.200	1.021	0.980
0.250	1.033	0.968
0.300	1.048	0.954
0.400	1.091	0.917
0.500	1.155	0.866
0.600	1.250	0.800
0.700	1.400	0.714
0.750	1.512	0.661
0.800	1.667	0.600
0.866	2.000	0.500
0.900	2.294	0.436
0.990	7.089	0.141
0.999	22.366	0.045
0.99995	100.00	0.010

Alternative representations

There are other ways to write the factor. Above, velocity v was used, but related variables such as momentum and rapidity may also be convenient.

Momentum

Solving the previous relativistic momentum equation for γ leads to

${\displaystyle \gamma ={\sqrt {1+\left({\frac {p}{m_{0}c}}\right)^{2}}}}$.

This form is rarely used, although it does appear in the Maxwell–Jüttner distribution.

Rapidity

Applying the definition of rapidity as the hyperbolic angle ${\displaystyle \varphi }$:

${\displaystyle \tanh \varphi =\beta }$

also leads to γ (by use of hyperbolic identities):

${\displaystyle \gamma =\cosh \varphi ={\frac {1}{\sqrt {1-\tanh ^{2}\varphi }}}={\frac {1}{\sqrt {1-\beta ^{2}}}}.}$

Using the property of Lorentz transformation, it can be shown that rapidity is additive, a useful property that velocity does not have. Thus the rapidity parameter forms a one-parameter group, a foundation for physical models.

Series expansion (velocity)

The Lorentz factor has the Maclaurin series:

${\displaystyle {\begin{aligned}\gamma &={\dfrac {1}{\sqrt {1-\beta ^{2}}}}\\&=\sum _{n=0}^{\infty }\beta ^{2n}\prod _{k=1}^{n}\left({\dfrac {2k-1}{2k}}\right)\\&=1+{\tfrac {1}{2}}\beta ^{2}+{\tfrac {3}{8}}\beta ^{4}+{\tfrac {5}{16}}\beta ^{6}+{\tfrac {35}{128}}\beta ^{8}+{\tfrac {63}{256}}\beta ^{10}+\cdots ,\\\end{aligned}}}$

which is a special case of a binomial series.

The approximation γ ≈ 1 + 1/2 β² may be used to calculate relativistic effects at low speeds. It holds to within 1% error for v < 0.4 c (v < 120,000 km/s), and to within 0.1% error for v < 0.22 c (v < 66,000 km/s). 

The truncated versions of this series also allow physicists to prove that special relativity reduces to Newtonian mechanics at low speeds. For example, in special relativity, the following two equations hold:

${\displaystyle {\begin{aligned}{\vec {p}}&=\gamma m{\vec {v}},\\E&=\gamma mc^{2}.\end{aligned}}}$

For γ ≈ 1 and γ ≈ 1 + 1/2 β², respectively, these reduce to their Newtonian equivalents:

${\displaystyle {\begin{aligned}{\vec {p}}&=m{\vec {v}},\\E&=mc^{2}+{\tfrac {1}{2}}mv^{2}.\end{aligned}}}$

The Lorentz factor equation can also be inverted to yield

${\displaystyle \beta ={\sqrt {1-{\frac {1}{\gamma ^{2}}}}}.}$

This has an asymptotic form

${\displaystyle \beta =1-{\tfrac {1}{2}}\gamma ^{-2}-{\tfrac {1}{8}}\gamma ^{-4}-{\tfrac {1}{16}}\gamma ^{-6}-{\tfrac {5}{128}}\gamma ^{-8}+\cdots }$.

The first two terms are occasionally used to quickly calculate velocities from large γ values. The approximation β ≈ 1 − 1/2 γ⁻² holds to within 1% tolerance for γ > 2, and to within 0.1% tolerance for γ > 3.5.

Applications in astronomy

The standard model of long-duration gamma-ray bursts (GRBs) holds that these explosions are ultra-relativistic (initial ${\displaystyle \gamma }$ greater than approximately 100), which is invoked to explain the so-called "compactness" problem: absent this ultra-relativistic expansion, the ejecta would be optically thick to pair production at typical peak spectral energies of a few 100 keV, whereas the prompt emission is observed to be non-thermal.

Subatomic particles called muons, have a relatively high lorentz factor and therefore experience extreme time dilation. As an example, muons generally have a mean lifetime of about 2.2 μs which means muons generated from cosmic ray collisions at about 10 km up in the atmosphere should be non-detectable on the ground due to their decay rate. However, it has been found that ~10% of muons are still detected on the surface, thereby proving that to be detectable they have had their decay rates slow down relative to our inertial frame of reference.

Novikov self-consistency principle

From Wikipedia, the free encyclopedia

 

The Novikov self-consistency principle, also known as the Novikov self-consistency conjecture and Larry Niven's law of conservation of history, is a principle developed by Russian physicist Igor Dmitriyevich Novikov in the mid-1980s. Novikov intended it to solve the problem of paradoxes in time travel, which is theoretically permitted in certain solutions of general relativity that contain what are known as closed timelike curves. The principle asserts that if an event exists that would cause a paradox or any "change" to the past whatsoever, then the probability of that event is zero. It would thus be impossible to create time paradoxes.

History

Physicists have long known that some solutions to the theory of general relativity contain closed timelike curves—for example the Gödel metric. Novikov discussed the possibility of closed timelike curves (CTCs) in books he wrote in 1975 and 1983, offering the opinion that only self-consistent trips back in time would be permitted. In a 1990 paper by Novikov and several others, "Cauchy problem in spacetimes with closed timelike curves", the authors state:

The only type of causality violation that the authors would find unacceptable is that embodied in the science-fiction concept of going backward in time and killing one's younger self ("changing the past"). Some years ago one of us (Novikov¹⁰) briefly considered the possibility that CTCs might exist and argued that they cannot entail this type of causality violation: events on a CTC are already guaranteed to be self-consistent, Novikov argued; they influence each other around a closed curve in a self-adjusted, cyclical, self-consistent way. The other authors recently have arrived at the same viewpoint.
We shall embody this viewpoint in a principle of self-consistency, which states that the only solutions to the laws of physics that can occur locally in the real Universe are those which are globally self-consistent. This principle allows one to build a local solution to the equations of physics only if that local solution can be extended to a part of a (not necessarily unique) global solution, which is well defined throughout the nonsingular regions of the space-time.

Among the co-authors of this 1990 paper were Kip Thorne, Mike Morris, and Ulvi Yurtsever, who in 1988 had stirred up renewed interest in the subject of time travel in general relativity with their paper "Wormholes, Time Machines, and the Weak Energy Condition", which showed that a new general relativity solution known as a traversable wormhole could lead to closed timelike curves, and unlike previous CTC-containing solutions, it did not require unrealistic conditions for the universe as a whole. After discussions with another co-author of the 1990 paper, John Friedman, they convinced themselves that time travel needn't lead to unresolvable paradoxes, regardless of the object sent through the wormhole.

"Polchinski's paradox"

 

Echeverria and Klinkhammer's resolution

 

By way of response, physicist Joseph Polchinski wrote them a letter arguing that one could avoid the issue of free will by considering a potentially paradoxical scenario involving a billiard ball sent back in time through a wormhole. In Polchinski's scenario, the billiard ball is fired into the wormhole at an angle such that, if it continues along its path, it will exit in the past at just the right angle to collide with its earlier self, knocking it off track and preventing it from entering the wormhole in the first place. Thorne would refer to this scenario as "Polchinski's paradox" in 1994.

Upon considering the scenario, Fernando Echeverria and Gunnar Klinkhammer, two students at Caltech (where Thorne taught), arrived at a solution to the problem that managed to avoid any inconsistencies. In the revised scenario, the ball emerges from the future at a different angle than the one that generates the paradox, and delivers its younger self a glancing blow instead of knocking it completely away from the wormhole. This blow alters its trajectory by just the right degree, meaning it will travel back in time with the angle required to deliver its younger self the necessary glancing blow. Echeverria and Klinkhammer actually found that there was more than one self-consistent solution, with slightly different angles for the glancing blow in each situation. Later analysis by Thorne and Robert Forward illustrated that for certain initial trajectories of the billiard ball, there could actually be an infinite number of self-consistent solutions.

Echeverria, Klinkhammer, and Thorne published a paper discussing these results in 1991; in addition, they reported that they had tried to see if they could find any initial conditions for the billiard ball for which there were no self-consistent extensions, but were unable to do so. Thus it is plausible that there exist self-consistent extensions for every possible initial trajectory, although this has not been proven. This only applies to initial conditions outside of the chronology-violating region of spacetime, which is bounded by a Cauchy horizon. This could mean that the Novikov self-consistency principle does not actually place any constraints on systems outside of the region of space-time where time travel is possible, only inside it. 

Even if self-consistent extensions can be found for arbitrary initial conditions outside the Cauchy Horizon, the finding that there can be multiple distinct self-consistent extensions for the same initial condition—indeed, Echeverria et al. found an infinite number of consistent extensions for every initial trajectory they analyzed—can be seen as problematic, since classically there seems to be no way to decide which extension the laws of physics will choose. To get around this difficulty, Thorne and Klinkhammer analyzed the billiard ball scenario using quantum mechanics, performing a quantum-mechanical sum over histories (path integral) using only the consistent extensions, and found that this resulted in a well-defined probability for each consistent extension. The authors of Cauchy problem in spacetimes with closed timelike curves write:

The simplest way to impose the principle of self-consistency in quantum mechanics (in a classical space-time) is by a sum-over-histories formulation in which one includes all those, and only those, histories that are self-consistent. It turns out that, at least formally (modulo such issues as the convergence of the sum), for every choice of the billiard ball's initial, nonrelativistic wave function before the Cauchy horizon, such a sum over histories produces unique, self-consistent probabilities for the outcomes of all sets of subsequent measurements. ... We suspect, more generally, that for any quantum system in a classical wormhole spacetime with a stable Cauchy horizon, the sum over all self-consistent histories will give unique, self-consistent probabilities for the outcomes of all sets of measurements that one might choose to make.

Assumptions

The Novikov consistency principle assumes certain conditions about what sort of time travel is possible. Specifically, it assumes either that there is only one timeline, or that any alternative timelines (such as those postulated by the many-worlds interpretation of quantum mechanics) are not accessible. 

Given these assumptions, the constraint that time travel must not lead to inconsistent outcomes could be seen merely as a tautology, a self-evident truth that can not possibly be false. However, the Novikov self-consistency principle is intended to go beyond just the statement that history must be consistent, making the additional nontrivial assumption that the universe obeys the same local laws of physics in situations involving time travel that it does in regions of space-time that lack closed timelike curves. This is clarified in the above-mentioned "Cauchy problem in spacetimes with closed timelike curves", where the authors write:

That the principle of self-consistency is not totally tautological becomes clear when one considers the following alternative: The laws of physics might permit CTCs; and when CTCs occur, they might trigger new kinds of local physics which we have not previously met. ... The principle of self-consistency is intended to rule out such behavior. It insists that local physics is governed by the same types of physical laws as we deal with in the absence of CTCs: the laws that entail self-consistent single valuedness for the fields. In essence, the principle of self-consistency is a principle of no new physics. If one is inclined from the outset to ignore or discount the possibility of new physics, then one will regard self-consistency as a trivial principle.

Implications for time travelers

The assumptions of the self-consistency principle can be extended to hypothetical scenarios involving intelligent time travelers as well as unintelligent objects such as billiard balls. The authors of "Cauchy problem in spacetimes with closed timelike curves" commented on the issue in the paper's conclusion, writing:

If CTCs are allowed, and if the above vision of theoretical physics' accommodation with them turns out to be more or less correct, then what will this imply about the philosophical notion of free will for humans and other intelligent beings? It certainly will imply that intelligent beings cannot change the past. Such change is incompatible with the principle of self-consistency. Consequently, any being who went through a wormhole and tried to change the past would be prevented by physical law from making the change; i.e., the "free will" of the being would be constrained. Although this constraint has a more global character than constraints on free will that follow from the standard, local laws of physics, it is not obvious to us that this constraint is more severe than those imposed by standard physical law.

Similarly, physicist and astronomer J. Craig Wheeler concludes that:

According to the consistency conjecture, any complex interpersonal interactions must work themselves out self-consistently so that there is no paradox. That is the resolution. This means, if taken literally, that if time machines exist, there can be no free will. You cannot will yourself to kill your younger self if you travel back in time. You can coexist, take yourself out for a beer, celebrate your birthday together, but somehow circumstances will dictate that you cannot behave in a way that leads to a paradox in time. Novikov supports this point of view with another argument: physics already restricts your free will every day. You may will yourself to fly or to walk through a concrete wall, but gravity and condensed-matter physics dictate that you cannot. Why, Novikov asks, is the consistency restriction placed on a time traveler any different?

Time-loop logic

Time-loop logic, coined by roboticist and futurist Hans Moravec, is a hypothetical system of computation that exploits the Novikov self-consistency principle to compute answers much faster than possible with the standard model of computational complexity using Turing machines. In this system, a computer sends a result of a computation backwards through time and relies upon the self-consistency principle to force the sent result to be correct, provided the machine can reliably receive information from the future and provided the algorithm and the underlying mechanism are formally correct. An incorrect result or no result can still be produced if the time travel mechanism or algorithm are not guaranteed to be accurate. 

A simple example is an iterative method algorithm. Moravec states:

Make a computing box that accepts an input, which represents an approximate solution to some problem, and produces an output that is an improved approximation. Conventionally you would apply such a computation repeatedly a finite number of times, and then settle for the better, but still approximate, result. Given an appropriate negative delay something else is possible: [...] the result of each iteration of the function is brought back in time to serve as the "first" approximation. As soon as the machine is activated, a so-called "fixed-point" of F, an input which produces an identical output, usually signaling a perfect answer, appears (by an extraordinary coincidence!) immediately and steadily. [...] If the iteration does not converge, that is, if F has no fixed point, the computer outputs and inputs will shut down or hover in an unlikely intermediate state.

Quantum computation with a negative delay

Physicist David Deutsch showed in 1991 that this model of computation could solve NP problems in polynomial time, and Scott Aaronson later extended this result to show that the model could also be used to solve PSPACE problems in polynomial time. Deutsch shows that quantum computation with a negative delay—backwards time travel—produces only self-consistent solutions, and the chronology-violating region imposes constraints that are not apparent through classical reasoning. Researchers published in 2014 a simulation in which they claim to have validated Deutsch's model with photons. However, it was shown in an article by Tolksdorf and Verch that Deutsch's self-consistency condition can be fulfilled to arbitrary precision in any quantum system described according to relativistic quantum field theory even on spacetimes which do not admit closed timelike curves, casting doubts on whether Deutsch's model is really characteristic of quantum processes simulating closed timelike curves in the sense of general relativity.

Scientific acceptance

General relativity researcher Matt Visser views causal loops and Novikov's self-consistency principle as an ad hoc solution and supposes that there are far more damaging implications of time travel. Time-travel researcher Serguei Krasnikov similarly finds no inherent fault in causal loops, but finds other problems with time travel in general relativity.

Hendrik Lorentz

From Wikipedia, the free encyclopedia

.

Hendrik Antoon Lorentz
Born	18 July 1853 Arnhem, Netherlands
Died	4 February 1928 (aged 74) Haarlem, Netherlands
Nationality	Netherlands
Alma mater	University of Leiden
Known for	Lorentz transformation Lorentz ether theory Theory of EM radiation Lorentz force Lorentz contraction Lorentzian metric Lorentz factor Rayleigh–Lorentz pendulum
Awards	Nobel Prize for Physics (1902) ForMemRS (1905) Rumford Medal (1908) Franklin Medal (1917) Copley Medal (1918)
Scientific career
Fields	Physics
Institutions	University of Leiden
Doctoral advisor	Pieter Rijke
Doctoral students	Geertruida L. de Haas-Lorentz Adriaan Fokker Leonard Ornstein Hendrika Johanna van Leeuwen

Hendrik Antoon Lorentz (/ˈlɒrənts/; 18 July 1853 – 4 February 1928) was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect. He also derived the transformation equations underpinning Albert Einstein's theory of special relativity.

According to the biography published by the Nobel Foundation, "It may well be said that Lorentz was regarded by all theoretical physicists as the world's leading spirit, who completed what was left unfinished by his predecessors and prepared the ground for the fruitful reception of the new ideas based on the quantum theory." He received many honours and distinctions, including a term as chairman of the International Committee on Intellectual Cooperation, the forerunner of UNESCO, between 1925 and 1928.

Biography

Early life

Hendrik Lorentz was born in Arnhem, Gelderland, Netherlands, the son of Gerrit Frederik Lorentz (1822–1893), a well-off horticulturist, and Geertruida van Ginkel (1826–1861). In 1862, after his mother's death, his father married Luberta Hupkes. Despite being raised as a Protestant, he was a freethinker in religious matters. From 1866 to 1869, he attended the "Hogere Burger School" in Arnhem, a new type of public high school recently established by Johan Rudolph Thorbecke. His results in school were exemplary; not only did he excel in the physical sciences and mathematics, but also in English, French, and German. In 1870, he passed the exams in classical languages which were then required for admission to University.

Lorentz studied physics and mathematics at the Leiden University, where he was strongly influenced by the teaching of astronomy professor Frederik Kaiser; it was his influence that led him to become a physicist. After earning a bachelor's degree, he returned to Arnhem in 1871 to teach night school classes in mathematics, but he continued his studies in Leiden in addition to his teaching position. In 1875, Lorentz earned a doctoral degree under Pieter Rijke on a thesis entitled "Over de theorie der terugkaatsing en breking van het licht" (On the theory of reflection and refraction of light), in which he refined the electromagnetic theory of James Clerk Maxwell.

Career

Professor in Leiden

Portrait by Jan Veth

 

On 17 November 1877, only 24 years of age, Hendrik Antoon Lorentz was appointed to the newly established chair in theoretical physics at the University of Leiden. The position had initially been offered to Johan van der Waals, but he accepted a position at the Universiteit van Amsterdam. On 25 January 1878, Lorentz delivered his inaugural lecture on "De moleculaire theoriën in de natuurkunde" (The molecular theories in physics). In 1881, he became member of the Royal Netherlands Academy of Arts and Sciences.

During the first twenty years in Leiden, Lorentz was primarily interested in the electromagnetic theory of electricity, magnetism, and light. After that, he extended his research to a much wider area while still focusing on theoretical physics. Lorentz made significant contributions to fields ranging from hydrodynamics to general relativity. His most important contributions were in the area of electromagnetism, the electron theory, and relativity.

Lorentz theorized that atoms might consist of charged particles and suggested that the oscillations of these charged particles were the source of light. When a colleague and former student of Lorentz's, Pieter Zeeman, discovered the Zeeman effect in 1896, Lorentz supplied its theoretical interpretation. The experimental and theoretical work was honored with the Nobel prize in physics in 1902. Lorentz' name is now associated with the Lorentz-Lorenz formula, the Lorentz force, the Lorentzian distribution, and the Lorentz transformation.

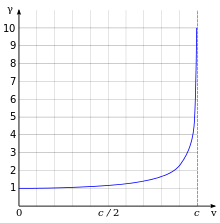
Electrodynamics and relativity

In 1892 and 1895, Lorentz worked on describing electromagnetic phenomena (the propagation of light) in reference frames that move relative to the postulated luminiferous aether. He discovered that the transition from one to another reference frame could be simplified by using a new time variable that he called local time and which depended on universal time and the location under consideration. Although Lorentz did not give a detailed interpretation of the physical significance of local time, with it, he could explain the aberration of light and the result of the Fizeau experiment. In 1900 and 1904, Henri Poincaré called local time Lorentz's "most ingenious idea" and illustrated it by showing that clocks in moving frames are synchronized by exchanging light signals that are assumed to travel at the same speed against and with the motion of the frame. In 1892, with the attempt to explain the Michelson-Morley experiment, Lorentz also proposed that moving bodies contract in the direction of motion.

In 1899 and again in 1904, Lorentz added time dilation to his transformations and published what Poincaré in 1905 named Lorentz transformations. It was apparently unknown to Lorentz that Joseph Larmor had used identical transformations to describe orbiting electrons in 1897. Larmor's and Lorentz's equations look somewhat dissimilar, but they are algebraically equivalent to those presented by Poincaré and Einstein in 1905. Lorentz's 1904 paper includes the covariant formulation of electrodynamics, in which electrodynamic phenomena in different reference frames are described by identical equations with well defined transformation properties. The paper clearly recognizes the significance of this formulation, namely that the outcomes of electrodynamic experiments do not depend on the relative motion of the reference frame. The 1904 paper includes a detailed discussion of the increase of the inertial mass of rapidly moving objects in a useless attempt to make momentum look exactly like Newtonian momentum; it was also an attempt to explain the length contraction as the accumulation of "stuff" onto mass making it slow and contract.

Lorentz and special relativity

Albert Einstein and Hendrik Antoon Lorentz, photographed by Ehrenfest in front of his home in Leiden in 1921.

 

Lorentz (left) at the International Committee on Intellectual Cooperation of the League of Nations, here with Albert Einstein.

 

In 1905, Einstein would use many of the concepts, mathematical tools and results Lorentz discussed to write his paper entitled "On the Electrodynamics of Moving Bodies", known today as the theory of special relativity. Because Lorentz laid the fundamentals for the work by Einstein, this theory was originally called the Lorentz-Einstein theory.

In 1906, Lorentz's electron theory received a full-fledged treatment in his lectures at Columbia University, published under the title The Theory of Electrons. 

The increase of mass was the first prediction of Lorentz and Einstein to be tested, but some experiments by Kaufmann appeared to show a slightly different mass increase; this led Lorentz to the famous remark that he was "au bout de mon latin" ("at the end of my [knowledge of] Latin" = at his wit's end) The confirmation of his prediction had to wait until 1908 and later.

Lorentz published a series of papers dealing with what he called "Einstein's principle of relativity". For instance, in 1909, 1910, 1914. In his 1906 lectures published with additions in 1909 in the book "The theory of electrons" (updated in 1915), he spoke affirmatively of Einstein's theory:

It will be clear by what has been said that the impressions received by the two observers A0 and A would be alike in all respects. It would be impossible to decide which of them moves or stands still with respect to the ether, and there would be no reason for preferring the times and lengths measured by the one to those determined by the other, nor for saying that either of them is in possession of the "true" times or the "true" lengths. This is a point which Einstein has laid particular stress on, in a theory in which he starts from what he calls the principle of relativity, [...] I cannot speak here of the many highly interesting applications which Einstein has made of this principle. His results concerning electromagnetic and optical phenomena ... agree in the main with those which we have obtained in the preceding pages, the chief difference being that Einstein simply postulates what we have deduced, with some difficulty and not altogether satisfactorily, from the fundamental equations of the electromagnetic field. By doing so, he may certainly take credit for making us see in the negative result of experiments like those of Michelson, Rayleigh and Brace, not a fortuitous compensation of opposing effects, but the manifestation of a general and fundamental principle. [...] It would be unjust not to add that, besides the fascinating boldness of its starting point, Einstein's theory has another marked advantage over mine. Whereas I have not been able to obtain for the equations referred to moving axes exactly the same form as for those which apply to a stationary system, Einstein has accomplished this by means of a system of new variables slightly different from those which I have introduced.

Though Lorentz still maintained that there is an (undetectable) aether in which resting clocks indicate the "true time":

1909: Yet, I think, something may also be claimed in favour of the form in which I have presented the theory. I cannot but regard the ether, which can be the seat of an electromagnetic field with its energy and its vibrations, as endowed with a certain degree of substantiality, however different it may be from all ordinary matter.
1910: Provided that there is an aether, then under all systems x, y, z, t, one is preferred by the fact, that the coordinate axes as well as the clocks are resting in the aether. If one connects with this the idea (which I would abandon only reluctantly) that space and time are completely different things, and that there is a "true time" (simultaneity thus would be independent of the location, in agreement with the circumstance that we can have the idea of infinitely great velocities), then it can be easily seen that this true time should be indicated by clocks at rest in the aether. However, if the relativity principle had general validity in nature, one wouldn't be in the position to determine, whether the reference system just used is the preferred one. Then one comes to the same results, as if one (following Einstein and Minkowski) deny the existence of the aether and of true time, and to see all reference systems as equally valid. Which of these two ways of thinking one is following, can surely be left to the individual.

Lorentz also gave credit to Poincaré's contributions to relativity.

Indeed, for some of the physical quantities which enter the formulas, I did not indicate the transformation which suits best. That was done by Poincaré and then by Mr. Einstein and Minkowski [...] I did not succeed in obtaining the exact invariance of the equations [...] Poincaré, on the contrary, obtained a perfect invariance of the equations of electrodynamics, and he formulated the "postulate of relativity", terms which he was the first to employ. [...] Let us add that by correcting the imperfections of my work he never reproached me for them.

Lorentz and general relativity

Lorentz was one of few scientists who supported Einstein's search for general relativity from the beginning – he wrote several research papers and discussed with Einstein personally and by letter. For instance, he attempted to combine Einstein's formalism with Hamilton's principle (1915), and to reformulate it in a coordinate-free way (1916). Lorentz wrote in 1919:

The total eclipse of the sun of May 29, resulted in a striking confirmation of the new theory of the universal attractive power of gravitation developed by Albert Einstein, and thus reinforced the conviction that the defining of this theory is one of the most important steps ever taken in the domain of natural science.

Lorentz and quantum mechanics

Lorentz gave a series of lectures in the Fall of 1926 at Cornell University on the new quantum mechanics; in these he presented Erwin Schrödinger's wave mechanics.

Assessments

Lorentz-monument Park Sonsbeek. Arnhem. Nederlands

Einstein wrote of Lorentz:

1928: The enormous significance of his work consisted therein, that it forms the basis for the theory of atoms and for the general and special theories of relativity. The special theory was a more detailed expose of those concepts which are found in Lorentz's research of 1895.
1953: For me personally he meant more than all the others I have met on my life's journey.

Poincaré (1902) said of Lorentz's theory of electrodynamics:

The most satisfactory theory is that of Lorentz; it is unquestionably the theory that best explains the known facts, the one that throws into relief the greatest number of known relations ... it is due to Lorentz that the results of Fizeau on the optics of moving bodies, the laws of normal and abnormal dispersion and of absorption are connected with each other ... Look at the ease with which the new Zeeman phenomenon found its place, and even aided the classification of Faraday's magnetic rotation, which had defied all Maxwell's efforts.

Paul Langevin (1911) said of Lorentz:

It will be Lorentz's main claim to fame that he demonstrated that the fundamental equations of electromagnetism also allow of a group of transformations that enables them to resume the same form when a transition is made from one reference system to another. This group differs fundamentally from the above group as regards transformations of space and time.''

Lorentz and Emil Wiechert had an interesting correspondence on the topics of electromagnetism and the theory of relativity, and Lorentz explained his ideas in letters to Wiechert.

Lorentz was chairman of the first Solvay Conference held in Brussels in the autumn of 1911. Shortly after the conference, Poincaré wrote an essay on quantum physics which gives an indication of Lorentz's status at the time:

... at every moment [the twenty physicists from different countries] could be heard talking of the [quantum mechanics] which they contrasted with the old mechanics. Now what was the old mechanics? Was it that of Newton, the one which still reigned uncontested at the close of the nineteenth century? No, it was the mechanics of Lorentz, the one dealing with the principle of relativity; the one which, hardly five years ago, seemed to be the height of boldness.

Change of priorities

In 1910, Lorentz decided to reorganize his life. His teaching and management duties at Leiden University were taking up too much of his time, leaving him little time for research. In 1912, he resigned from his chair of theoretical physics to become curator of the "Physics Cabinet" at Teylers Museum in Haarlem. He remained connected to Leiden University as an external professor, and his "Monday morning lectures" on new developments in theoretical physics soon became legendary.

Lorentz initially asked Einstein to succeed him as professor of theoretical physics at Leiden. However, Einstein could not accept because he had just accepted a position at ETH Zurich. Einstein had no regrets in this matter, since the prospect of having to fill Lorentz's shoes made him shiver. Instead Lorentz appointed Paul Ehrenfest as his successor in the chair of theoretical physics at the Leiden University, who would found the Institute for Theoretical Physics which would become known as the Lorentz Institute.

Civil work

After World War I, Lorentz was one of the driving forces behind the founding of the "Wetenschappelijke Commissie van Advies en Onderzoek in het Belang van Volkswelvaart en Weerbaarheid", a committee which was to harness the scientific potential united in the Royal Netherlands Academy of Arts and Sciences (KNAW) for solving civil problems such as food shortage which had resulted from the war. Lorentz was appointed chair of the committee. However, despite the best efforts of many of the participants the committee would harvest little success. The only exception being that it ultimately resulted in the founding of TNO, the Netherlands Organisation for Applied Scientific Research.

Lorentz was also asked by the Dutch government to chair a committee to calculate some of the effects of the proposed Afsluitdijk (Enclosure Dam) flood control dam on water levels in the Waddenzee. Hydraulic engineering was mainly an empirical science at that time, but the disturbance of the tidal flow caused by the Afsluitdijk was so unprecedented that the empirical rules could not be trusted. Originally Lorentz was only supposed to have a coordinating role in the committee, but it quickly became apparent that Lorentz was the only physicist to have any fundamental traction on the problem. In the period 1918 till 1926, Lorentz invested a large portion of his time in the problem. Lorentz proposed to start from the basic hydrodynamic equations of motion and solve the problem numerically. This was feasible for a "human computer", because of the quasi-one-dimensional nature of the water flow in the Waddenzee. The Afsluitdijk was completed in 1932, and the predictions of Lorentz and his committee turned out to be remarkably accurate. One of the two sets of locks in the Afsluitdijk was named after him.

Family life

In 1881, Lorentz married Aletta Catharina Kaiser. Her father was J.W. Kaiser, a professor at the Academy of Fine Arts. He was the Director of the museum which later became the well-known Rijksmuseum (National Gallery). He also was the designer of the first postage stamps of The Netherlands. 

There were two daughters, and one son from this marriage.

Dr. Geertruida Luberta Lorentz, the eldest daughter, was a physicist. She married Professor W.J. de Haas, who was the Director of the Cryogenic Laboratory at the University of Leiden.

Death

In January 1928, Lorentz became seriously ill, and died shortly after on February 4. The respect in which he was held in the Netherlands is apparent from Owen Willans Richardson's description of his funeral:

The funeral took place at Haarlem at noon on Friday, February 10. At the stroke of twelve the State telegraph and telephone services of Holland were suspended for three minutes as a revered tribute to the greatest man the Netherlands has produced in our time. It was attended by many colleagues and distinguished physicists from foreign countries. The President, Sir Ernest Rutherford, represented the Royal Society and made an appreciative oration by the graveside.

— O. W. Richardson

Unique 1928 film footage of the funeral procession with a lead carriage followed by ten mourners, followed by a carriage with the coffin, followed in turn by at least four more carriages, passing by a crowd at the Grote Markt, Haarlem from the Zijlstraat to the Smedestraat, and then back again through the Grote Houtstraat towards the Barteljorisstraat, on the way to the "Algemene Begraafplaats" at the Kleverlaan (northern Haarlem cemetery) has been digitized on YouTube. Einstein gave a eulogy at a memorial service at Leiden University.

Legacy

Lorentz is considered one of the prime representatives of the "Second Dutch Golden Age", a period of several decades surrounding 1900 in which in the natural sciences in the Netherlands flourished.

Richardson describes Lorentz as:

[A] man of remarkable intellectual powers ... . Although steeped in his own investigation of the moment, he always seemed to have in his immediate grasp its ramifications into every corner of the universe. ... The singular clearness of his writings provides a striking reflection of his wonderful powers in this respect. .... He possessed and successfully employed the mental vivacity which is necessary to follow the interplay of discussion, the insight which is required to extract those statements which illuminate the real difficulties, and the wisdom to lead the discussion among fruitful channels, and he did this so skillfully that the process was hardly perceptible.

M. J. Klein (1967) wrote of Lorentz's reputation in the 1920s:

For many years physicists had always been eager "to hear what Lorentz will say about it" when a new theory was advanced, and, even at seventy-two, he did not disappoint them.

In addition to the Nobel prize, Lorentz received a great many honours for his outstanding work. He was elected a Foreign Member of the Royal Society (ForMemRS) in 1905. The Society awarded him their Rumford Medal in 1908 and their Copley Medal in 1918. He was elected an Honorary Member of the Netherlands Chemical Society in 1912.