Condensed matter physics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Condensed_matter_physics

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with "condensed" phases of matter: systems of many constituents with strong interactions between them. More exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theories to develop mathematical models.

The diversity of systems and phenomena available for study makes condensed matter physics the most active field of contemporary physics: one third of all American physicists self-identify as condensed matter physicists, and the Division of Condensed Matter Physics is the largest division at the American Physical Society. The field overlaps with chemistry, materials science, engineering and nanotechnology, and relates closely to atomic physics and biophysics. The theoretical physics of condensed matter shares important concepts and methods with that of particle physics and nuclear physics.

A variety of topics in physics such as crystallography, metallurgy, elasticity, magnetism, etc., were treated as distinct areas until the 1940s, when they were grouped together as solid-state physics. Around the 1960s, the study of physical properties of liquids was added to this list, forming the basis for the more comprehensive specialty of condensed matter physics. The Bell Telephone Laboratories was one of the first institutes to conduct a research program in condensed matter physics. According to founding director of the Max Planck Institute for Solid State Research, physics professor Manuel Cardona, it was Albert Einstein who created the modern field of condensed matter physics starting with his seminal 1905 article on the photoelectric effect and photoluminescence which opened the fields of photoelectron spectroscopy and photoluminescence spectroscopy, and later his 1907 article on the specific heat of solids which introduced, for the first time, the effect of lattice vibrations on the thermodynamic properties of crystals, in particular the specific heat. Deputy Director of the Yale Quantum Institute A. Douglas Stone makes a similar priority case for Einstein in his work on the synthetic history of quantum mechanics.

Etymology

According to physicist Philip Warren Anderson, the use of the term "condensed matter" to designate a field of study was coined by him and Volker Heine, when they changed the name of their group at the Cavendish Laboratories, Cambridge from Solid state theory to Theory of Condensed Matter in 1967, as they felt it better included their interest in liquids, nuclear matter, and so on. Although Anderson and Heine helped popularize the name "condensed matter", it had been used in Europe for some years, most prominently in the Springer-Verlag journal Physics of Condensed Matter, launched in 1963. The name "condensed matter physics" emphasized the commonality of scientific problems encountered by physicists working on solids, liquids, plasmas, and other complex matter, whereas "solid state physics" was often associated with restricted industrial applications of metals and semiconductors. In the 1960s and 70s, some physicists felt the more comprehensive name better fit the funding environment and Cold War politics of the time.

References to "condensed" states can be traced to earlier sources. For example, in the introduction to his 1947 book Kinetic Theory of Liquids, Yakov Frenkel proposed that "The kinetic theory of liquids must accordingly be developed as a generalization and extension of the kinetic theory of solid bodies. As a matter of fact, it would be more correct to unify them under the title of 'condensed bodies'".

History of condensed matter physics

Classical physics

Heike Kamerlingh Onnes and Johannes van der Waals with the helium liquefactor at Leiden in 1908

One of the first studies of condensed states of matter was by English chemist Humphry Davy, in the first decades of the nineteenth century. Davy observed that of the forty chemical elements known at the time, twenty-six had metallic properties such as lustre, ductility and high electrical and thermal conductivity. This indicated that the atoms in John Dalton's atomic theory were not indivisible as Dalton claimed, but had inner structure. Davy further claimed that elements that were then believed to be gases, such as nitrogen and hydrogen could be liquefied under the right conditions and would then behave as metals.^{[14][note 1]}

In 1823, Michael Faraday, then an assistant in Davy's lab, successfully liquefied chlorine and went on to liquefy all known gaseous elements, except for nitrogen, hydrogen, and oxygen. Shortly after, in 1869, Irish chemist Thomas Andrews studied the phase transition from a liquid to a gas and coined the term critical point to describe the condition where a gas and a liquid were indistinguishable as phases, and Dutch physicist Johannes van der Waals supplied the theoretical framework which allowed the prediction of critical behavior based on measurements at much higher temperatures. By 1908, James Dewar and Heike Kamerlingh Onnes were successfully able to liquefy hydrogen and then newly discovered helium, respectively.

Paul Drude in 1900 proposed the first theoretical model for a classical electron moving through a metallic solid. Drude's model described properties of metals in terms of a gas of free electrons, and was the first microscopic model to explain empirical observations such as the Wiedemann–Franz law. However, despite the success of Drude's free electron model, it had one notable problem: it was unable to correctly explain the electronic contribution to the specific heat and magnetic properties of metals, and the temperature dependence of resistivity at low temperatures.

In 1911, three years after helium was first liquefied, Onnes working at University of Leiden discovered superconductivity in mercury, when he observed the electrical resistivity of mercury to vanish at temperatures below a certain value. The phenomenon completely surprised the best theoretical physicists of the time, and it remained unexplained for several decades. Albert Einstein, in 1922, said regarding contemporary theories of superconductivity that "with our far-reaching ignorance of the quantum mechanics of composite systems we are very far from being able to compose a theory out of these vague ideas."

Advent of quantum mechanics

Drude's classical model was augmented by Wolfgang Pauli, Arnold Sommerfeld, Felix Bloch and other physicists. Pauli realized that the free electrons in metal must obey the Fermi–Dirac statistics. Using this idea, he developed the theory of paramagnetism in 1926. Shortly after, Sommerfeld incorporated the Fermi–Dirac statistics into the free electron model and made it better to explain the heat capacity. Two years later, Bloch used quantum mechanics to describe the motion of an electron in a periodic lattice. The mathematics of crystal structures developed by Auguste Bravais, Yevgraf Fyodorov and others was used to classify crystals by their symmetry group, and tables of crystal structures were the basis for the series International Tables of Crystallography, first published in 1935. Band structure calculations was first used in 1930 to predict the properties of new materials, and in 1947 John Bardeen, Walter Brattain and William Shockley developed the first semiconductor-based transistor, heralding a revolution in electronics.

A replica of the first point-contact transistor in Bell labs

In 1879, Edwin Herbert Hall working at the Johns Hopkins University discovered a voltage developed across conductors transverse to an electric current in the conductor and magnetic field perpendicular to the current. This phenomenon arising due to the nature of charge carriers in the conductor came to be termed the Hall effect, but it was not properly explained at the time, since the electron was not experimentally discovered until 18 years later. After the advent of quantum mechanics, Lev Landau in 1930 developed the theory of Landau quantization and laid the foundation for the theoretical explanation for the quantum Hall effect discovered half a century later.

Magnetism as a property of matter has been known in China since 4000 BC. However, the first modern studies of magnetism only started with the development of electrodynamics by Faraday, Maxwell and others in the nineteenth century, which included classifying materials as ferromagnetic, paramagnetic and diamagnetic based on their response to magnetization. Pierre Curie studied the dependence of magnetization on temperature and discovered the Curie point phase transition in ferromagnetic materials. In 1906, Pierre Weiss introduced the concept of magnetic domains to explain the main properties of ferromagnets. The first attempt at a microscopic description of magnetism was by Wilhelm Lenz and Ernst Ising through the Ising model that described magnetic materials as consisting of a periodic lattice of spins that collectively acquired magnetization. The Ising model was solved exactly to show that spontaneous magnetization cannot occur in one dimension but is possible in higher-dimensional lattices. Further research such as by Bloch on spin waves and Néel on antiferromagnetism led to developing new magnetic materials with applications to magnetic storage devices.

Modern many-body physics

A magnet levitating above a high-temperature superconductor. Today some physicists are working to understand high-temperature superconductivity using the AdS/CFT correspondence.

The Sommerfeld model and spin models for ferromagnetism illustrated the successful application of quantum mechanics to condensed matter problems in the 1930s. However, there still were several unsolved problems, most notably the description of superconductivity and the Kondo effect. After World War II, several ideas from quantum field theory were applied to condensed matter problems. These included recognition of collective excitation modes of solids and the important notion of a quasiparticle. Russian physicist Lev Landau used the idea for the Fermi liquid theory wherein low energy properties of interacting fermion systems were given in terms of what are now termed Landau-quasiparticles. Landau also developed a mean-field theory for continuous phase transitions, which described ordered phases as spontaneous breakdown of symmetry. The theory also introduced the notion of an order parameter to distinguish between ordered phases. Eventually in 1956, John Bardeen, Leon Cooper and John Schrieffer developed the so-called BCS theory of superconductivity, based on the discovery that arbitrarily small attraction between two electrons of opposite spin mediated by phonons in the lattice can give rise to a bound state called a Cooper pair.

The quantum Hall effect: Components of the Hall resistivity as a function of the external magnetic field

The study of phase transitions and the critical behavior of observables, termed critical phenomena, was a major field of interest in the 1960s. Leo Kadanoff, Benjamin Widom and Michael Fisher developed the ideas of critical exponents and widom scaling. These ideas were unified by Kenneth G. Wilson in 1972, under the formalism of the renormalization group in the context of quantum field theory.

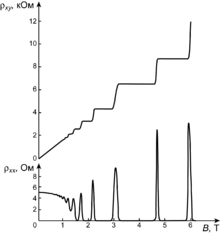
The quantum Hall effect was discovered by Klaus von Klitzing, Dorda and Pepper in 1980 when they observed the Hall conductance to be integer multiples of a fundamental constant ${\displaystyle e^2/h}$.(see figure) The effect was observed to be independent of parameters such as system size and impurities. In 1981, theorist Robert Laughlin proposed a theory explaining the unanticipated precision of the integral plateau. It also implied that the Hall conductance is proportional to a topological invariant, called Chern number, whose relevance for the band structure of solids was formulated by David J. Thouless and collaborators. Shortly after, in 1982, Horst Störmer and Daniel Tsui observed the fractional quantum Hall effect where the conductance was now a rational multiple of the constant ${\displaystyle e^2/h}$. Laughlin, in 1983, realized that this was a consequence of quasiparticle interaction in the Hall states and formulated a variational method solution, named the Laughlin wavefunction. The study of topological properties of the fractional Hall effect remains an active field of research. Decades later, the aforementioned topological band theory advanced by David J. Thouless and collaborators was further expanded leading to the discovery of topological insulators.

In 1986, Karl Müller and Johannes Bednorz discovered the first high temperature superconductor, a material which was superconducting at temperatures as high as 50 kelvins. It was realized that the high temperature superconductors are examples of strongly correlated materials where the electron–electron interactions play an important role. A satisfactory theoretical description of high-temperature superconductors is still not known and the field of strongly correlated materials continues to be an active research topic.

In 2009, David Field and researchers at Aarhus University discovered spontaneous electric fields when creating prosaic films of various gases. This has more recently expanded to form the research area of spontelectrics.

In 2012, several groups released preprints which suggest that samarium hexaboride has the properties of a topological insulator in accord with the earlier theoretical predictions. Since samarium hexaboride is an established Kondo insulator, i.e. a strongly correlated electron material, it is expected that the existence of a topological Dirac surface state in this material would lead to a topological insulator with strong electronic correlations.

Theoretical

Theoretical condensed matter physics involves the use of theoretical models to understand properties of states of matter. These include models to study the electronic properties of solids, such as the Drude model, the band structure and the density functional theory. Theoretical models have also been developed to study the physics of phase transitions, such as the Ginzburg–Landau theory, critical exponents and the use of mathematical methods of quantum field theory and the renormalization group. Modern theoretical studies involve the use of numerical computation of electronic structure and mathematical tools to understand phenomena such as high-temperature superconductivity, topological phases, and gauge symmetries.

Emergence

Main article: Emergence

Theoretical understanding of condensed matter physics is closely related to the notion of emergence, wherein complex assemblies of particles behave in ways dramatically different from their individual constituents. For example, a range of phenomena related to high temperature superconductivity are understood poorly, although the microscopic physics of individual electrons and lattices is well known. Similarly, models of condensed matter systems have been studied where collective excitations behave like photons and electrons, thereby describing electromagnetism as an emergent phenomenon. Emergent properties can also occur at the interface between materials: one example is the lanthanum aluminate-strontium titanate interface, where two band-insulators are joined to create conductivity and superconductivity.

Electronic theory of solids

Main article: Electronic band structure

The metallic state has historically been an important building block for studying properties of solids. The first theoretical description of metals was given by Paul Drude in 1900 with the Drude model, which explained electrical and thermal properties by describing a metal as an ideal gas of then-newly discovered electrons. He was able to derive the empirical Wiedemann-Franz law and get results in close agreement with the experiments. This classical model was then improved by Arnold Sommerfeld who incorporated the Fermi–Dirac statistics of electrons and was able to explain the anomalous behavior of the specific heat of metals in the Wiedemann–Franz law. In 1912, The structure of crystalline solids was studied by Max von Laue and Paul Knipping, when they observed the X-ray diffraction pattern of crystals, and concluded that crystals get their structure from periodic lattices of atoms. In 1928, Swiss physicist Felix Bloch provided a wave function solution to the Schrödinger equation with a periodic potential, known as Bloch's theorem.

Calculating electronic properties of metals by solving the many-body wavefunction is often computationally hard, and hence, approximation methods are needed to obtain meaningful predictions. The Thomas–Fermi theory, developed in the 1920s, was used to estimate system energy and electronic density by treating the local electron density as a variational parameter. Later in the 1930s, Douglas Hartree, Vladimir Fock and John Slater developed the so-called Hartree–Fock wavefunction as an improvement over the Thomas–Fermi model. The Hartree–Fock method accounted for exchange statistics of single particle electron wavefunctions. In general, it is very difficult to solve the Hartree–Fock equation. Only the free electron gas case can be solved exactly. Finally in 1964–65, Walter Kohn, Pierre Hohenberg and Lu Jeu Sham proposed the density functional theory (DFT) which gave realistic descriptions for bulk and surface properties of metals. The density functional theory has been widely used since the 1970s for band structure calculations of variety of solids.

Symmetry breaking

Main article: Symmetry breaking

Some states of matter exhibit symmetry breaking, where the relevant laws of physics possess some form of symmetry that is broken. A common example is crystalline solids, which break continuous translational symmetry. Other examples include magnetized ferromagnets, which break rotational symmetry, and more exotic states such as the ground state of a BCS superconductor, that breaks U(1) phase rotational symmetry.

Goldstone's theorem in quantum field theory states that in a system with broken continuous symmetry, there may exist excitations with arbitrarily low energy, called the Goldstone bosons. For example, in crystalline solids, these correspond to phonons, which are quantized versions of lattice vibrations.

Phase transition

Main article: Phase transition

Phase transition refers to the change of phase of a system, which is brought about by change in an external parameter such as temperature. Classical phase transition occurs at finite temperature when the order of the system was destroyed. For example, when ice melts and becomes water, the ordered crystal structure is destroyed.

In quantum phase transitions, the temperature is set to absolute zero, and the non-thermal control parameter, such as pressure or magnetic field, causes the phase transitions when order is destroyed by quantum fluctuations originating from the Heisenberg uncertainty principle. Here, the different quantum phases of the system refer to distinct ground states of the Hamiltonian matrix. Understanding the behavior of quantum phase transition is important in the difficult tasks of explaining the properties of rare-earth magnetic insulators, high-temperature superconductors, and other substances.

Two classes of phase transitions occur: first-order transitions and second-order or continuous transitions. For the latter, the two phases involved do not co-exist at the transition temperature, also called the critical point. Near the critical point, systems undergo critical behavior, wherein several of their properties such as correlation length, specific heat, and magnetic susceptibility diverge exponentially. These critical phenomena present serious challenges to physicists because normal macroscopic laws are no longer valid in the region, and novel ideas and methods must be invented to find the new laws that can describe the system.

The simplest theory that can describe continuous phase transitions is the Ginzburg–Landau theory, which works in the so-called mean-field approximation. However, it can only roughly explain continuous phase transition for ferroelectrics and type I superconductors which involves long range microscopic interactions. For other types of systems that involves short range interactions near the critical point, a better theory is needed.

Near the critical point, the fluctuations happen over broad range of size scales while the feature of the whole system is scale invariant. Renormalization group methods successively average out the shortest wavelength fluctuations in stages while retaining their effects into the next stage. Thus, the changes of a physical system as viewed at different size scales can be investigated systematically. The methods, together with powerful computer simulation, contribute greatly to the explanation of the critical phenomena associated with continuous phase transition.

Experimental

Experimental condensed matter physics involves the use of experimental probes to try to discover new properties of materials. Such probes include effects of electric and magnetic fields, measuring response functions, transport properties and thermometry. Commonly used experimental methods include spectroscopy, with probes such as X-rays, infrared light and inelastic neutron scattering; study of thermal response, such as specific heat and measuring transport via thermal and heat conduction.

Image of X-ray diffraction pattern from a protein crystal.

Scattering

Further information: Scattering

Several condensed matter experiments involve scattering of an experimental probe, such as X-ray, optical photons, neutrons, etc., on constituents of a material. The choice of scattering probe depends on the observation energy scale of interest. Visible light has energy on the scale of 1 electron volt (eV) and is used as a scattering probe to measure variations in material properties such as dielectric constant and refractive index. X-rays have energies of the order of 10 keV and hence are able to probe atomic length scales, and are used to measure variations in electron charge density.

Neutrons can also probe atomic length scales and are used to study scattering off nuclei and electron spins and magnetization (as neutrons have spin but no charge). Coulomb and Mott scattering measurements can be made by using electron beams as scattering probes. Similarly, positron annihilation can be used as an indirect measurement of local electron density. Laser spectroscopy is an excellent tool for studying the microscopic properties of a medium, for example, to study forbidden transitions in media with nonlinear optical spectroscopy.

External magnetic fields

In experimental condensed matter physics, external magnetic fields act as thermodynamic variables that control the state, phase transitions and properties of material systems. Nuclear magnetic resonance (NMR) is a method by which external magnetic fields are used to find resonance modes of individual electrons, thus giving information about the atomic, molecular, and bond structure of their neighborhood. NMR experiments can be made in magnetic fields with strengths up to 60 tesla. Higher magnetic fields can improve the quality of NMR measurement data. Quantum oscillations is another experimental method where high magnetic fields are used to study material properties such as the geometry of the Fermi surface. High magnetic fields will be useful in experimentally testing of the various theoretical predictions such as the quantized magnetoelectric effect, image magnetic monopole, and the half-integer quantum Hall effect.

Nuclear spectroscopy

The local structure, the structure of the nearest neighbour atoms, of condensed matter can be investigated with methods of nuclear spectroscopy, which are very sensitive to small changes. Using specific and radioactive nuclei, the nucleus becomes the probe that interacts with its surrounding electric and magnetic fields (hyperfine interactions). The methods are suitable to study defects, diffusion, phase change, magnetism. Common methods are e.g. NMR, Mössbauer spectroscopy, or perturbed angular correlation (PAC). Especially PAC is ideal for the study of phase changes at extreme temperature above 2000 °C due to no temperature dependence of the method.

Cold atomic gases

Main article: Optical lattice

 

The first Bose–Einstein condensate observed in a gas of ultracold rubidium atoms. The blue and white areas represent higher density.

Ultracold atom trapping in optical lattices is an experimental tool commonly used in condensed matter physics, and in atomic, molecular, and optical physics. The method involves using optical lasers to form an interference pattern, which acts as a lattice, in which ions or atoms can be placed at very low temperatures. Cold atoms in optical lattices are used as quantum simulators, that is, they act as controllable systems that can model behavior of more complicated systems, such as frustrated magnets. In particular, they are used to engineer one-, two- and three-dimensional lattices for a Hubbard model with pre-specified parameters, and to study phase transitions for antiferromagnetic and spin liquid ordering.

In 1995, a gas of rubidium atoms cooled down to a temperature of 170 nK was used to experimentally realize the Bose–Einstein condensate, a novel state of matter originally predicted by S. N. Bose and Albert Einstein, wherein a large number of atoms occupy one quantum state.

Applications

Computer simulation of nanogears made of fullerene molecules. It is hoped that advances in nanoscience will lead to machines working on the molecular scale.

Research in condensed matter physics has given rise to several device applications, such as the development of the semiconductor transistor, laser technology, and several phenomena studied in the context of nanotechnology. Methods such as scanning-tunneling microscopy can be used to control processes at the nanometer scale, and have given rise to the study of nanofabrication. Such molecular machines were developed for example by Nobel laurate in chemistry Ben Feringa. He and his team developed multiple molecular machines such as molecular car, molecular windmill and many more.

In quantum computation, information is represented by quantum bits, or qubits. The qubits may decohere quickly before useful computation is completed. This serious problem must be solved before quantum computing may be realized. To solve this problem, several promising approaches are proposed in condensed matter physics, including Josephson junction qubits, spintronic qubits using the spin orientation of magnetic materials, or the topological non-Abelian anyons from fractional quantum Hall effect states.

Condensed matter physics also has important uses for biophysics, for example, the experimental method of magnetic resonance imaging, which is widely used in medical diagnosis.

Micro black hole

From Wikipedia, the free encyclopedia

Micro black holes, also called mini black holes or quantum mechanical black holes, are hypothetical tiny (<1 M_☉) black holes, for which quantum mechanical effects play an important role. The concept that black holes may exist that are smaller than stellar mass was introduced in 1971 by Stephen Hawking.

It is possible that such black holes were created in the high-density environment of the early Universe (or Big Bang), or possibly through subsequent phase transitions (referred to as primordial black holes). They might be observed by astrophysicists through the particles they are expected to emit by Hawking radiation.

Some hypotheses involving additional space dimensions predict that micro black holes could be formed at energies as low as the TeV range, which are available in particle accelerators such as the Large Hadron Collider. Popular concerns have then been raised over end-of-the-world scenarios (see Safety of particle collisions at the Large Hadron Collider). However, such quantum black holes would instantly evaporate, either totally or leaving only a very weakly interacting residue. Beside the theoretical arguments, cosmic rays hitting the Earth do not produce any damage, although they reach energies in the range of hundreds of TeV.

Minimum mass of a black hole

In an early speculation, Stephen Hawking conjectured that a black hole would not form with a mass below about 10⁻⁸ kg (roughly the Planck mass). To make a black hole, one must concentrate mass or energy sufficiently that the escape velocity from the region in which it is concentrated exceeds the speed of light.

Some extensions of present physics posit the existence of extra dimensions of space. In higher-dimensional spacetime, the strength of gravity increases more rapidly with decreasing distance than in three dimensions. With certain special configurations of the extra dimensions, this effect can lower the Planck scale to the TeV range. Examples of such extensions include large extra dimensions, special cases of the Randall–Sundrum model, and string theory configurations like the GKP solutions. In such scenarios, black hole production could possibly be an important and observable effect at the Large Hadron Collider (LHC). It would also be a common natural phenomenon induced by cosmic rays.

All this assumes that the theory of general relativity remains valid at these small distances. If it does not, then other, currently unknown, effects might limit the minimum size of a black hole. Elementary particles are equipped with a quantum-mechanical, intrinsic angular momentum (spin). The correct conservation law for the total (orbital plus spin) angular momentum of matter in curved spacetime requires that spacetime is equipped with torsion. The simplest and most natural theory of gravity with torsion is the Einstein–Cartan theory. Torsion modifies the Dirac equation in the presence of the gravitational field and causes fermion particles to be spatially extended. In this case the spatial extension of fermions limits the minimum mass of a black hole to be on the order of 10¹⁶ kg, showing that micro black holes may not exist. The energy necessary to produce such a black hole is 39 orders of magnitude greater than the energies available at the Large Hadron Collider, indicating that the LHC cannot produce mini black holes. But if black holes are produced, then the theory of general relativity is proven wrong and does not exist at these small distances. The rules of general relativity would be broken, as is consistent with theories of how matter, space, and time break down around the event horizon of a black hole. This would prove the spatial extensions of the fermion limits to be incorrect as well. The fermion limits assume a minimum mass needed to sustain a black hole, as opposed to the opposite, the minimum mass needed to start a black hole, which in theory is achievable in the LHC under some conditions.

Stability

Hawking radiation

Main article: Hawking radiation

In 1975, Stephen Hawking argued that, due to quantum effects, black holes "evaporate" by a process now referred to as Hawking radiation in which elementary particles (such as photons, electrons, quarks and gluons) are emitted. His calculations showed that the smaller the size of the black hole, the faster the evaporation rate, resulting in a sudden burst of particles as the micro black hole suddenly explodes.

Any primordial black hole of sufficiently low mass will evaporate to near the Planck mass within the lifetime of the Universe. In this process, these small black holes radiate away matter. A rough picture of this is that pairs of virtual particles emerge from the vacuum near the event horizon, with one member of a pair being captured, and the other escaping the vicinity of the black hole. The net result is the black hole loses mass (due to conservation of energy). According to the formulae of black hole thermodynamics, the more the black hole loses mass, the hotter it becomes, and the faster it evaporates, until it approaches the Planck mass. At this stage, a black hole would have a Hawking temperature of T_P/8π (5.6×10³⁰ K), which means an emitted Hawking particle would have an energy comparable to the mass of the black hole. Thus, a thermodynamic description breaks down. Such a micro black hole would also have an entropy of only 4π nats, approximately the minimum possible value. At this point then, the object can no longer be described as a classical black hole, and Hawking's calculations also break down.

While Hawking radiation is sometimes questioned, Leonard Susskind summarizes an expert perspective in his book The Black Hole War: "Every so often, a physics paper will appear claiming that black holes don't evaporate. Such papers quickly disappear into the infinite junk heap of fringe ideas."

Conjectures for the final state

Conjectures for the final fate of the black hole include total evaporation and production of a Planck-mass-sized black hole remnant. Such Planck-mass black holes may in effect be stable objects if the quantized gaps between their allowed energy levels bar them from emitting Hawking particles or absorbing energy gravitationally like a classical black hole. In such case, they would be weakly interacting massive particles; this could explain dark matter.

Primordial black holes

Main article: Primordial black hole

Formation in the early Universe

Production of a black hole requires concentration of mass or energy within the corresponding Schwarzschild radius. It was hypothesized by Zel'dovich and Novikov first and independently by Hawking that, shortly after the Big Bang, the Universe was dense enough for any given region of space to fit within its own Schwarzschild radius. Even so, at that time, the Universe was not able to collapse into a singularity due to its uniform mass distribution and rapid growth. This, however, does not fully exclude the possibility that black holes of various sizes may have emerged locally. A black hole formed in this way is called a primordial black hole and is the most widely accepted hypothesis for the possible creation of micro black holes. Computer simulations suggest that the probability of formation of a primordial black hole is inversely proportional to its mass. Thus, the most likely outcome would be micro black holes.

Expected observable effects

A primordial black hole with an initial mass of around 10¹² kg would be completing its evaporation today; a less massive primordial black hole would have already evaporated. Under optimal conditions, the Fermi Gamma-ray Space Telescope satellite, launched in June 2008, might detect experimental evidence for evaporation of nearby black holes by observing gamma ray bursts. It is unlikely that a collision between a microscopic black hole and an object such as a star or a planet would be noticeable. The small radius and high density of the black hole would allow it to pass straight through any object consisting of normal atoms, interacting with only few of its atoms while doing so. It has, however, been suggested that a small black hole of sufficient mass passing through the Earth would produce a detectable acoustic or seismic signal. On the moon, it may leave a distinct type of crater, still visible after billions of years.

Human-made micro black holes

Feasibility of production

Further information: Kugelblitz (astrophysics)

In familiar three-dimensional gravity, the minimum energy of a microscopic black hole is 10¹⁶ TeV (equivalent to 1.6 GJ or 444 kWh), which would have to be condensed into a region on the order of the Planck length. This is far beyond the limits of any current technology. It is estimated that to collide two particles to within a distance of a Planck length with currently achievable magnetic field strengths would require a ring accelerator about 1,000 light years in diameter to keep the particles on track.

However, in some scenarios involving extra dimensions of space, the Planck mass can be as low as the TeV range. The Large Hadron Collider (LHC) has a design energy of 14 TeV for proton–proton collisions and 1,150 TeV for Pb–Pb collisions. It was argued in 2001 that, in these circumstances, black hole production could be an important and observable effect at the LHC or future higher-energy colliders. Such quantum black holes should decay emitting sprays of particles that could be seen by detectors at these facilities. A paper by Choptuik and Pretorius, published in 2010 in Physical Review Letters, presented a computer-generated proof that micro black holes must form from two colliding particles with sufficient energy, which might be allowable at the energies of the LHC if additional dimensions are present other than the customary four (three spatial, one temporal).

Safety arguments

Main article: Safety of high-energy particle collision experiments

Hawking's calculation and more general quantum mechanical arguments predict that micro black holes evaporate almost instantaneously. Additional safety arguments beyond those based on Hawking radiation were given in the paper, which showed that in hypothetical scenarios with stable micro black holes massive enough to destroy Earth, such black holes would have been produced by cosmic rays and would have likely already destroyed astronomical objects such as planets, stars, or stellar remnants such as neutron stars and white dwarfs.

Black holes in quantum theories of gravity

It is possible, in some theories of quantum gravity, to calculate the quantum corrections to ordinary, classical black holes. Contrarily to conventional black holes, which are solutions of gravitational field equations of the general theory of relativity, quantum gravity black holes incorporate quantum gravity effects in the vicinity of the origin, where classically a curvature singularity occurs. According to the theory employed to model quantum gravity effects, there are different kinds of quantum gravity black holes, namely loop quantum black holes, non-commutative black holes, and asymptotically safe black holes. In these approaches, black holes are singularity-free.

Virtual micro black holes were proposed by Stephen Hawking in 1995 and by Fabio Scardigli in 1999 as part of a Grand Unified Theory as a quantum gravity candidate.

Cosmic string

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Cosmic_string

Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry-breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking was not simply connected. Their existence was first contemplated by the theoretical physicist Tom Kibble in the 1970s.

The formation of cosmic strings is somewhat analogous to the imperfections that form between crystal grains in solidifying liquids, or the cracks that form when water freezes into ice. The phase transitions leading to the production of cosmic strings are likely to have occurred during the earliest moments of the universe's evolution, just after cosmological inflation, and are a fairly generic prediction in both quantum field theory and string theory models of the early universe.

Theories containing cosmic strings

In string theory, the role of cosmic strings can be played by the fundamental strings (or F-strings) themselves that define the theory perturbatively, by D-strings which are related to the F-strings by weak-strong or so called S-duality, or higher-dimensional D-, NS- or M-branes that are partially wrapped on compact cycles associated to extra spacetime dimensions so that only one non-compact dimension remains.

The prototypical example of a quantum field theory with cosmic strings is the Abelian Higgs model. The quantum field theory and string theory cosmic strings are expected to have many properties in common, but more research is needed to determine the precise distinguishing features. The F-strings for instance are fully quantum-mechanical and do not have a classical definition, whereas the field theory cosmic strings are almost exclusively treated classically.

Dimensions

Cosmic strings, if they exist, would be extremely thin with diameters of the same order of magnitude as that of a proton, i.e. ~ 1 fm, or smaller. Given that this scale is much smaller than any cosmological scale, these strings are often studied in the zero-width, or Nambu–Goto approximation. Under this assumption strings behave as one-dimensional objects and obey the Nambu–Goto action, which is classically equivalent to the Polyakov action that defines the bosonic sector of superstring theory.

In field theory, the string width is set by the scale of the symmetry breaking phase transition. In string theory, the string width is set (in the simplest cases) by the fundamental string scale, warp factors (associated to the spacetime curvature of an internal six-dimensional spacetime manifold) and/or the size of internal compact dimensions. (In string theory, the universe is either 10- or 11-dimensional, depending on the strength of interactions and the curvature of spacetime.)

Gravitation

A string is a geometrical deviation from Euclidean geometry in spacetime characterized by an angular deficit: a circle around the outside of a string would comprise a total angle less than 360°. From the general theory of relativity such a geometrical defect must be in tension, and would be manifested by mass. Even though cosmic strings are thought to be extremely thin, they would have immense density, and so would represent significant gravitational wave sources. A cosmic string about a kilometer in length may be more massive than the Earth.

However general relativity predicts that the gravitational potential of a straight string vanishes: there is no gravitational force on static surrounding matter. The only gravitational effect of a straight cosmic string is a relative deflection of matter (or light) passing the string on opposite sides (a purely topological effect). A closed cosmic string gravitates in a more conventional way.

During the expansion of the universe, cosmic strings would form a network of loops, and in the past it was thought that their gravity could have been responsible for the original clumping of matter into galactic superclusters. It is now calculated that their contribution to the structure formation in the universe is less than 10%.

Negative mass cosmic string

The standard model of a cosmic string is a geometrical structure with an angle deficit, which thus is in tension and hence has positive mass. In 1995, Visser et al. proposed that cosmic strings could theoretically also exist with angle excesses, and thus negative tension and hence negative mass. The stability of such exotic matter strings is problematic; however, they suggested that if a negative mass string were to be wrapped around a wormhole in the early universe, such a wormhole could be stabilized sufficiently to exist in the present day.

Super-critical cosmic string

The exterior geometry of a (straight) cosmic string can be visualized in an embedding diagram as follows: Focusing on the two-dimensional surface perpendicular to the string, its geometry is that of a cone which is obtained by cutting out a wedge of angle δ and gluing together the edges. The angular deficit δ is linearly related to the string tension (= mass per unit length), i.e. the larger the tension, the steeper the cone. Therefore, δ reaches 2π for a certain critical value of the tension, and the cone degenerates to a cylinder. (In visualizing this setup one has to think of a string with a finite thickness.) For even larger, "super-critical" values, δ exceeds 2π and the (two-dimensional) exterior geometry closes up (it becomes compact), ending in a conical singularity.

However, this static geometry is unstable in the super-critical case (unlike for sub-critical tensions): Small perturbations lead to a dynamical spacetime which expands in axial direction at a constant rate. The 2D exterior is still compact, but the conical singularity can be avoided, and the embedding picture is that of a growing cigar. For even larger tensions (exceeding the critical value by approximately a factor of 1.6), the string cannot be stabilized in radial direction anymore.

Realistic cosmic strings are expected to have tensions around 6 orders of magnitude below the critical value, and are thus always sub-critical. However, the inflating cosmic string solutions might be relevant in the context of brane cosmology, where the string is promoted to a 3-brane (corresponding to our universe) in a six-dimensional bulk.

Observational evidence

It was once thought that the gravitational influence of cosmic strings might contribute to the large-scale clumping of matter in the universe, but all that is known today through galaxy surveys and precision measurements of the cosmic microwave background (CMB) fits an evolution out of random, gaussian fluctuations. These precise observations therefore tend to rule out a significant role for cosmic strings and currently it is known that the contribution of cosmic strings to the CMB cannot be more than 10%.

The violent oscillations of cosmic strings generically lead to the formation of cusps and kinks. These in turn cause parts of the string to pinch off into isolated loops. These loops have a finite lifespan and decay (primarily) via gravitational radiation. This radiation which leads to the strongest signal from cosmic strings may in turn be detectable in gravitational wave observatories. An important open question is to what extent do the pinched off loops backreact or change the initial state of the emitting cosmic string—such backreaction effects are almost always neglected in computations and are known to be important, even for order of magnitude estimates.

Gravitational lensing of a galaxy by a straight section of a cosmic string would produce two identical, undistorted images of the galaxy. In 2003 a group led by Mikhail Sazhin reported the accidental discovery of two seemingly identical galaxies very close together in the sky, leading to speculation that a cosmic string had been found. However, observations by the Hubble Space Telescope in January 2005 showed them to be a pair of similar galaxies, not two images of the same galaxy. A cosmic string would produce a similar duplicate image of fluctuations in the cosmic microwave background, which it was thought might have been detectable by the Planck Surveyor mission. However, a 2013 analysis of data from the Planck mission failed to find any evidence of cosmic strings.

A piece of evidence supporting cosmic string theory is a phenomenon noticed in observations of the "double quasar" called Q0957+561A,B. Originally discovered by Dennis Walsh, Bob Carswell, and Ray Weymann in 1979, the double image of this quasar is caused by a galaxy positioned between it and the Earth. The gravitational lens effect of this intermediate galaxy bends the quasar's light so that it follows two paths of different lengths to Earth. The result is that we see two images of the same quasar, one arriving a short time after the other (about 417.1 days later). However, a team of astronomers at the Harvard-Smithsonian Center for Astrophysics led by Rudolph Schild studied the quasar and found that during the period between September 1994 and July 1995 the two images appeared to have no time delay; changes in the brightness of the two images occurred simultaneously on four separate occasions. Schild and his team believe that the only explanation for this observation is that a cosmic string passed between the Earth and the quasar during that time period traveling at very high speed and oscillating with a period of about 100 days.

Currently the most sensitive bounds on cosmic string parameters come from the non-detection of gravitational waves by pulsar timing array data. The earthbound Laser Interferometer Gravitational-Wave Observatory (LIGO) and especially the space-based gravitational wave detector Laser Interferometer Space Antenna (LISA) will search for gravitational waves and are likely to be sensitive enough to detect signals from cosmic strings, provided the relevant cosmic string tensions are not too small.

String theory and cosmic strings

During the early days of string theory both string theorists and cosmic string theorists believed that there was no direct connection between superstrings and cosmic strings (the names were chosen independently by analogy with ordinary string). The possibility of cosmic strings being produced in the early universe was first envisioned by quantum field theorist Tom Kibble in 1976, and this sprouted the first flurry of interest in the field. In 1985, during the first superstring revolution, Edward Witten contemplated on the possibility of fundamental superstrings having been produced in the early universe and stretched to macroscopic scales, in which case (following the nomenclature of Tom Kibble) they would then be referred to as cosmic superstrings. He concluded that had they been produced they would have either disintegrated into smaller strings before ever reaching macroscopic scales (in the case of Type I superstring theory), they would always appear as boundaries of domain walls whose tension would force the strings to collapse rather than grow to cosmic scales (in the context of heterotic superstring theory), or having a characteristic energy scale close to the Planck energy they would be produced before cosmological inflation and hence be diluted away with the expansion of the universe and not be observable.

Much has changed since these early days, primarily due to the second superstring revolution. It is now known that string theory in addition to the fundamental strings which define the theory perturbatively also contains other one-dimensional objects, such as D-strings, and higher-dimensional objects such as D-branes, NS-branes and M-branes partially wrapped on compact internal spacetime dimensions, while being spatially extended in one non-compact dimension. The possibility of large compact dimensions and large warp factors allows strings with tension much lower than the Planck scale. Furthermore, various dualities that have been discovered point to the conclusion that actually all these apparently different types of string are just the same object as it appears in different regions of parameter space. These new developments have largely revived interest in cosmic strings, starting in the early 2000s.

In 2002, Henry Tye and collaborators predicted the production of cosmic superstrings during the last stages of brane inflation, a string theory construction of the early universe that gives leads to an expanding universe and cosmological inflation. It was subsequently realized by string theorist Joseph Polchinski that the expanding Universe could have stretched a "fundamental" string (the sort which superstring theory considers) until it was of intergalactic size. Such a stretched string would exhibit many of the properties of the old "cosmic" string variety, making the older calculations useful again. As theorist Tom Kibble remarks, "string theory cosmologists have discovered cosmic strings lurking everywhere in the undergrowth". Older proposals for detecting cosmic strings could now be used to investigate superstring theory.

Superstrings, D-strings or the other stringy objects mentioned above stretched to intergalactic scales would radiate gravitational waves, which could be detected using experiments like LIGO and especially the space-based gravitational wave experiment LISA. They might also cause slight irregularities in the cosmic microwave background, too subtle to have been detected yet but possibly within the realm of future observability.

Note that most of these proposals depend, however, on the appropriate cosmological fundamentals (strings, branes, etc.), and no convincing experimental verification of these has been confirmed to date. Cosmic strings nevertheless provide a window into string theory. If cosmic strings are observed which is a real possibility for a wide range of cosmological string models this would provide the first experimental evidence of a string theory model underlying the structure of spacetime.