W and Z bosons

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/W_and_Z_bosons 

 

W^±
and Z⁰
Bosons

Composition	Elementary particle
Statistics	Bosonic
Family	Gauge boson
Interactions	W: Weak, electromagnetic Z: Weak
Theorized	Glashow, Weinberg, Salam (1968)
Discovered	UA1 and UA2 collaborations, CERN, 1983
Mass	W: 80.3692±0.0133 GeV/c2 (2024) Z: 91.1880±0.0020 GeV/c2
Decay width	W: 2.085±0.042 GeV Z: 2.4955±0.0023 GeV
Electric charge	W: ±1 e Z: 0 e
Spin	1 ħ
Weak isospin	W: ±1 Z: 0
Weak hypercharge	0

In particle physics, the W and Z bosons are vector bosons that are together known as the weak bosons or more generally as the intermediate vector bosons. These elementary particles mediate the weak interaction; the respective symbols are W⁺
, W⁻
, and Z⁰
. The W^±
 bosons have either a positive or negative electric charge of 1 elementary charge and are each other's antiparticles. The Z⁰
 boson is electrically neutral and is its own antiparticle. The three particles each have a spin of 1. The W^±
 bosons have a magnetic moment, but the Z⁰
has none. All three of these particles are very short-lived, with a half-life of about 3×10⁻²⁵ s. Their experimental discovery was pivotal in establishing what is now called the Standard Model of particle physics.

The W bosons are named after the weak force. The physicist Steven Weinberg named the additional particle the "Z particle", and later gave the explanation that it was the last additional particle needed by the model. The W bosons had already been named, and the Z bosons were named for having zero electric charge.

The two W bosons are verified mediators of neutrino absorption and emission. During these processes, the W^±
 boson charge induces electron or positron emission or absorption, thus causing nuclear transmutation.

The Z boson mediates the transfer of momentum, spin and energy when neutrinos scatter elastically from matter (a process which conserves charge). Such behavior is almost as common as inelastic neutrino interactions and may be observed in bubble chambers upon irradiation with neutrino beams. The Z boson is not involved in the absorption or emission of electrons or positrons. Whenever an electron is observed as a new free particle, suddenly moving with kinetic energy, it is inferred to be a result of a neutrino interacting with the electron (with the momentum transfer via the Z boson) since this behavior happens more often when the neutrino beam is present. In this process, the neutrino scatters off the electron (via exchange of a boson), transferring some of the neutrino's momentum to the electron.

Basic properties

These bosons are among the heavyweights of the elementary particles. With masses of 80.4 GeV/c² and 91.2 GeV/c², respectively, the W and Z bosons are almost 80 times as massive as the proton – each heavier than an atom of iron.

Their high masses limit the range of the weak interaction. By way of contrast, the photon is the force carrier of the electromagnetic force and has zero mass, consistent with the infinite range of electromagnetism; the hypothetical graviton is also expected to have zero mass. (Although gluons are also presumed to have zero mass, the range of the strong nuclear force is limited for different reasons; see Color confinement.)

All three bosons have particle spin s = 1 ħ. The emission of a W⁺
or W⁻
 boson either lowers or raises the electric charge of the emitting particle by one unit, and also alters the spin by one unit. At the same time, the emission or absorption of a W^±
 boson can change the type of the particle – for example changing a strange quark into an up quark. The neutral Z boson cannot change the electric charge of any particle, nor can it change any other of the so-called "charges" (such as strangeness, baryon number, charm, etc.). The emission or absorption of a Z⁰
 boson can only change the spin, momentum, and energy of the other particle. (See also Weak neutral current.)

Relations to the weak nuclear force

The Feynman diagram for beta decay of a neutron into a proton, electron, and electron antineutrino via an intermediate W⁻
 boson

The W and Z bosons are carrier particles that mediate the weak nuclear force, much as the photon is the carrier particle for the electromagnetic force.

W bosons

The W^±
 bosons are best known for their role in nuclear decay. Consider, for example, the beta decay of cobalt-60.

⁶⁰
₂₇Co → ⁶⁰
₂₈Ni⁺ + e⁻
+ ν
_e

This reaction does not involve the whole cobalt-60 nucleus, but affects only one of its 33 neutrons. The neutron is converted into a proton while also emitting an electron (often called a beta particle in this context) and an electron antineutrino:

n⁰
→ p⁺
+ e⁻
+ ν
_e

Again, the neutron is not an elementary particle but a composite of an up quark and two down quarks (udd). It is one of the down quarks that interacts in beta decay, turning into an up quark to form a proton (uud). At the most fundamental level, then, the weak force changes the flavour of a single quark:

d → u + W⁻

which is immediately followed by decay of the W⁻
itself:

W⁻
→ e⁻
+ ν
_e

Z bosons

The Z⁰
 boson is its own antiparticle. Thus, all of its flavour quantum numbers and charges are zero. The exchange of a Z boson between particles, called a neutral current interaction, therefore leaves the interacting particles unaffected, except for a transfer of spin and/or momentum.

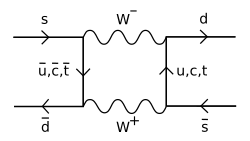
Z boson interactions involving neutrinos have distinct signatures: They provide the only known mechanism for elastic scattering of neutrinos in matter; neutrinos are almost as likely to scatter elastically (via Z boson exchange) as inelastically (via W boson exchange). Weak neutral currents via Z boson exchange were confirmed shortly thereafter (also in 1973), in a neutrino experiment in the Gargamelle bubble chamber at CERN.

Predictions of the W⁺, W⁻ and Z⁰ bosons

A Feynman diagram showing the exchange of a pair of W bosons. This is one of the leading terms contributing to neutral Kaon oscillation.

Following the success of quantum electrodynamics in the 1950s, attempts were undertaken to formulate a similar theory of the weak nuclear force. This culminated around 1968 in a unified theory of electromagnetism and weak interactions by Sheldon Glashow, Steven Weinberg, and Abdus Salam, for which they shared the 1979 Nobel Prize in Physics. Their electroweak theory postulated not only the W bosons necessary to explain beta decay, but also a new Z boson that had never been observed.

The fact that the W and Z bosons have mass while photons are massless was a major obstacle in developing electroweak theory. These particles are accurately described by an SU(2) gauge theory, but the bosons in a gauge theory must be massless. As a case in point, the photon is massless because electromagnetism is described by a U(1) gauge theory. Some mechanism is required to break the SU(2) symmetry, giving mass to the W and Z in the process. The Higgs mechanism, first put forward by the 1964 PRL symmetry breaking papers, fulfills this role. It requires the existence of another particle, the Higgs boson, which has since been found at the Large Hadron Collider. Of the four components of a Goldstone boson created by the Higgs field, three are absorbed by the W⁺
, Z⁰
, and W⁻
 bosons to form their longitudinal components, and the remainder appears as the spin-0 Higgs boson.

The combination of the SU(2) gauge theory of the weak interaction, the electromagnetic interaction, and the Higgs mechanism is known as the Glashow–Weinberg–Salam model. Today it is widely accepted as one of the pillars of the Standard Model of particle physics, particularly given the 2012 discovery of the Higgs boson by the CMS and ATLAS experiments.

The model predicts that W^±
and Z⁰
 bosons have the following masses:

${\displaystyle \begin{array}{rl}{m}_{{\text{W}}^{\pm }}& =\frac{1}{2}vg\\ m_{{\text{Z}}^0}& =\frac{1}{2}v\sqrt{g^2+{g^{\prime }}^2}\end{array}}$

where ${\displaystyle g}$ is the SU(2) gauge coupling, ${\displaystyle g^{\prime }}$ is the U(1) gauge coupling, and ${\displaystyle v}$ is the Higgs vacuum expectation value.

Discovery

The Gargamelle bubble chamber, now exhibited at CERN

Unlike beta decay, the observation of neutral current interactions that involve particles other than neutrinos requires huge investments in particle accelerators and particle detectors, such as are available in only a few high-energy physics laboratories in the world (and then only after 1983). This is because Z bosons behave in somewhat the same manner as photons, but do not become important until the energy of the interaction is comparable with the relatively huge mass of the Z boson.

The discovery of the W and Z bosons was considered a major success for CERN. First, in 1973, came the observation of neutral current interactions as predicted by electroweak theory. The huge Gargamelle bubble chamber photographed the tracks produced by neutrino interactions and observed events where a neutrino interacted but did not produce a corresponding lepton. This is a hallmark of a neutral current interaction and is interpreted as a neutrino exchanging an unseen Z boson with a proton or neutron in the bubble chamber. The neutrino is otherwise undetectable, so the only observable effect is the momentum imparted to the proton or neutron by the interaction.

The discovery of the W and Z bosons themselves had to wait for the construction of a particle accelerator powerful enough to produce them. The first such machine that became available was the Super Proton Synchrotron, where unambiguous signals of W bosons were seen in January 1983 during a series of experiments made possible by Carlo Rubbia and Simon van der Meer. The actual experiments were called UA1 (led by Rubbia) and UA2 (led by Pierre Darriulat), and were the collaborative effort of many people. Van der Meer was the driving force on the accelerator end (stochastic cooling). UA1 and UA2 found the Z boson a few months later, in May 1983. Rubbia and van der Meer were promptly awarded the 1984 Nobel Prize in Physics, a most unusual step for the conservative Nobel Foundation.

The W⁺
, W⁻
, and Z⁰
 bosons, together with the photon (γ), comprise the four gauge bosons of the electroweak interaction.

Measurements of W boson mass

In May 2024, the Particle Data Group estimated the World Average mass for the W boson to be 80369.2 ± 13.3 MeV, based on experiments to date.

As of 2021, experimental measurements of the W boson mass had been similarly assessed to converge around 80379±12 MeV, all consistent with one another and with the Standard Model.

In April 2022, a new analysis of historical data from the Fermilab Tevatron collider before its closure in 2011 determined the mass of the W boson to be 80433±9 MeV, which was seven standard deviations above that predicted by the Standard Model. Besides being inconsistent with the Standard Model, the new measurement was also inconsistent with previous measurements such as ATLAS. This suggests that either the old or the new measurements had an unexpected systematic error, such as an undetected quirk in the equipment. This led to careful reevaluation of this data analysis and other historical measurement, as well as the planning of future measurements to confirm the potential new result. Fermilab Deputy Director Joseph Lykken reiterated that "... the (new) measurement needs to be confirmed by another experiment before it can be interpreted fully."

In 2023, an improved ATLAS experiment measured the W boson mass at 80360±16 MeV, aligning with predictions from the Standard Model.

The Particle Data Group convened a working group on the Tevatron measurement of W boson mass, including W-mass experts from all hadron collider experiments to date, to understand the discrepancy. In May 2024 they concluded that the CDF measurement was an outlier, and the best estimate of the mass came from leaving out that measurement from the meta-analysis. "The corresponding value of the W boson mass is m_W = 80369.2±13.3 MeV, which we quote as the World Average."

In September 2024, the CMS experiment measured the W boson mass at 80360.2±9.9 MeV/c². This was the most precise measurement to date, obtained from observations of a large number of W → μν decays.

Decay

The W and Z bosons decay to fermion pairs but neither the W nor the Z bosons have sufficient energy to decay into the highest-mass top quark. Neglecting phase space effects and higher order corrections, simple estimates of their branching fractions can be calculated from the coupling constants.

W bosons

W bosons can decay to a lepton and antilepton (one of them charged and another neutral) or to a quark and antiquark of complementary types (with opposite electric charges ⁠±+1/3⁠ e and ⁠∓+2/3⁠ e). The decay width of the W boson to a quark–antiquark pair is proportional to the corresponding squared CKM matrix element and the number of quark colours, N_C = 3. The decay widths for the W⁺ boson are then proportional to:

Leptons		Quarks
e+ ν e	1	ud	3 ${\displaystyle |V_{\text{ud}}{|}^2}$	us	3 ${\displaystyle |V_{\text{us}}{|}^2}$	ub	3 ${\displaystyle |V_{\text{ub}}{|}^2}$
μ+ ν μ	1	cd	3 ${\displaystyle |V_{\text{cd}}{|}^2}$	cs	3 ${\displaystyle |V_{\text{cs}}{|}^2}$	cb	3 ${\displaystyle |V_{\text{cb}}{|}^2}$
τ+ ν τ	1	Energy conservation forbids decay to t.

Here, e⁺
, μ⁺
, τ⁺
denote the three flavours of leptons (more exactly, the positive charged antileptons). ν
_e, ν
_μ, ν
_τ denote the three flavours of neutrinos. The other particles, starting with u and d, all denote quarks and antiquarks (factor N_C is applied). The various ${\displaystyle V_{ij}}$ denote the corresponding CKM matrix coefficients.

Unitarity of the CKM matrix implies that ${\displaystyle |V_{\text{ud}}{|}^2+|V_{\text{us}}{|}^2+|V_{\text{ub}}{|}^2=}$ ${\displaystyle |V_{\text{cd}}{|}^2+|V_{\text{cs}}{|}^2+|V_{\text{cb}}{|}^2=1,}$ thus each of two quark rows sums to 3. Therefore, the leptonic branching ratios of the W boson are approximately ${\displaystyle B({\mathrm{e}}^{+}{\nu }_{\mathrm{e}})=}$${\displaystyle B({\mu }^{+}{\nu }_{\mu })=}$${\displaystyle B({\tau }^{+}{\nu }_{\tau })=}$ ⁠1/9⁠. The hadronic branching ratio is dominated by the CKM-favored ud and cs final states. The sum of the hadronic branching ratios has been measured experimentally to be 67.60±0.27%, with ${\displaystyle B({\ell }^{+}{\nu }_{\ell })=}$ 10.80±0.09%.

Z⁰ boson

See also: Weak charge

Z bosons decay into a fermion and its antiparticle. As the Z⁰
 boson is a mixture of the pre-symmetry-breaking W⁰
and B⁰
 bosons (see weak mixing angle), each vertex factor includes a factor ⁠${\displaystyle T_3-Q{\sin }^2{\theta }_{\text{W}}}$⁠, where ${\displaystyle T_3}$ is the third component of the weak isospin of the fermion (the "charge" for the weak force), ${\displaystyle Q}$ is the electric charge of the fermion (in units of the elementary charge), and ${\displaystyle {\theta }_{\text{w}}}$ is the weak mixing angle. Because the weak isospin ${\displaystyle (T_3)}$ is different for fermions of different chirality, either left-handed or right-handed, the coupling is different as well.

The relative strengths of each coupling can be estimated by considering that the decay rates include the square of these factors, and all possible diagrams (e.g. sum over quark families, and left and right contributions). The results tabulated below are just estimates, since they only include tree-level interaction diagrams in the Fermi theory.

Particles		Weak isospin ${\displaystyle (T_3)}$		Relative factor	Branching ratio
Name	Symbols	LEFT	RIGHT		Predicted for x = 0.23	Experimental measurements
Neutrinos (all)	ν e, ν μ, ν τ	⁠ 1 / 2 ⁠	0	3 (⁠ 1 / 2 ⁠)2	20.5%	20.00±0.06%
Charged leptons (all)	e− , μ− , τ−			3 (−⁠ 1 / 2 ⁠ + x)2 + 3 x2	10.2%	10.097±0.003%
Electron	e−	−⁠ 1 / 2 ⁠ + x	x	(−⁠ 1 / 2 ⁠ + x)2 + x2	3.4%	3.363±0.004%
Muon	μ−	−⁠ 1 / 2 ⁠ + x	x	(−⁠ 1 / 2 ⁠ + x)2 + x2	3.4%	3.366±0.007%
Tau	τ−	−⁠ 1 / 2 ⁠ + x	x	(−⁠ 1 / 2 ⁠ + x)2 + x 2	3.4%	3.367±0.008%
Hadrons					69.2%	69.91±0.06%
Down-type quarks	d, s, b	−⁠ 1 / 2 ⁠ + ⁠ 1 / 3 ⁠x	⁠1/3⁠x	3 (−⁠ 1 / 2 ⁠ + ⁠ 1 / 3 ⁠x)2 + 3 (⁠ 1 / 3 ⁠x)2	15.2%	15.6±0.4%
Up-type quarks (* except t)	u, c	⁠+ 1 / 2 ⁠ − ⁠ 2 / 3 ⁠x	−⁠ 2 / 3 ⁠x	3 (⁠+ 1 / 2 ⁠ − ⁠ 2 / 3 ⁠x)2 + 3 (−⁠ 2 / 3 ⁠x)2	11.8%	11.6±0.6%

To keep the notation compact, the table uses ⁠${\displaystyle x={\sin }^2{\theta }_{\text{w}}\approx \frac{1}{4}}$⁠.

* The impossible decay into a top quark–antiquark pair is left out of the table.

Subheadings LEFT and RIGHT denote the chirality or "handedness" of the fermions.

In 2018, the CMS collaboration observed the first exclusive decay of the Z boson to a ψ meson and a lepton–antilepton pair.

Grand Unified Theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Grand_Unified_Theory

 

Beyond the Standard Model
Simulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons

A Grand Unified Theory (GUT) is any model in particle physics that merges the electromagnetic, weak, and strong forces (the three gauge interactions of the Standard Model) into a single force at high energies. Although this unified force has not been directly observed, many GUT models theorize its existence. If the unification of these three interactions is possible, it raises the possibility that there was a grand unification epoch in the very early universe in which these three fundamental interactions were not yet distinct.

Experiments have confirmed that at high energy, the electromagnetic interaction and weak interaction unify into a single combined electroweak interaction. GUT models predict that at even higher energy, the strong and electroweak interactions will unify into one electronuclear interaction. This interaction is characterized by one larger gauge symmetry and thus several force carriers, but one unified coupling constant. Unifying gravity with the electronuclear interaction would provide a more comprehensive theory of everything (TOE) rather than a Grand Unified Theory. Thus, GUTs are often seen as an intermediate step towards a TOE.

The novel particles predicted by GUT models are expected to have extremely high masses—around the GUT scale of 10¹⁶ GeV/c² (only three orders of magnitude below the Planck scale of 10¹⁹ GeV/c²)—and so are well beyond the reach of any foreseen particle hadron collider experiments. Therefore, the particles predicted by GUT models will be unable to be observed directly, and instead the effects of grand unification might be detected through indirect observations of the following:

• proton decay,
• electric dipole moments of elementary particles,
• or the properties of neutrinos.

Some GUTs, such as the Pati–Salam model, predict the existence of magnetic monopoles.

While GUTs might be expected to offer simplicity over the complications present in the Standard Model, realistic models remain complicated because they need to introduce additional fields and interactions, or even additional dimensions of space, in order to reproduce observed fermion masses and mixing angles. This difficulty, in turn, may be related to the existence of family symmetries beyond the conventional GUT models. Due to this and the lack of any observed effect of grand unification so far, there is no generally accepted GUT model.

Models that do not unify the three interactions using one simple group as the gauge symmetry but do so using semisimple groups can exhibit similar properties and are sometimes referred to as Grand Unified Theories as well.

Unsolved problem in physics

Are the three forces of the Standard Model unified at high energies? By which symmetry is this unification governed? Can the Grand Unification Theory explain the number of fermion generations and their masses?

History

Historically, the first true GUT, which was based on the simple Lie group SU(5), was proposed by Howard Georgi and Sheldon Glashow in 1974. The Georgi–Glashow model was preceded by the semisimple Lie algebra Pati–Salam model by Abdus Salam and Jogesh Pati also in 1974, who pioneered the idea to unify gauge interactions.

The acronym GUT was first coined in 1978 by CERN researchers John Ellis, Andrzej Buras, Mary K. Gaillard, and Dimitri Nanopoulos, however in the final version of their paper they opted for the less anatomical GUM (Grand Unification Mass). Nanopoulos later that year was the first to use the acronym in a paper.

Motivation

The fact that the electric charges of electrons and protons seem to cancel each other exactly to extreme precision is essential for the existence of the macroscopic world as we know it, but this important property of elementary particles is not explained in the Standard Model of particle physics. While the description of strong and weak interactions within the Standard Model is based on gauge symmetries governed by the simple symmetry groups SU(3) and SU(2) which allow only discrete charges, the remaining component, the weak hypercharge interaction is described by an abelian symmetry U(1) which in principle allows for arbitrary charge assignments. The observed charge quantization, namely the postulation that all known elementary particles carry electric charges which are exact multiples of one-third of the "elementary" charge, has led to the idea that hypercharge interactions and possibly the strong and weak interactions might be embedded in one Grand Unified interaction described by a single, larger simple symmetry group containing the Standard Model. This would automatically predict the quantized nature and values of all elementary particle charges. Since this also results in a prediction for the relative strengths of the fundamental interactions which we observe, in particular, the weak mixing angle, grand unification ideally reduces the number of independent input parameters but is also constrained by observations.

Grand unification is reminiscent of the unification of electric and magnetic forces by Maxwell's field theory of electromagnetism in the 19th century, but its physical implications and mathematical structure are qualitatively different.

Unification of matter particles

For an elementary introduction to how Lie algebras are related to particle physics, see Particle physics and representation theory.

Schematic representation of fermions and bosons in SU(5) GUT showing 5 + 10 split in the multiplets. Neutral bosons (photon, Z-boson, and neutral gluons) are not shown but occupy the diagonal entries of the matrix in complex superpositions.

SU(5)

Main article: Georgi–Glashow model

The pattern of weak isospins, weak hypercharges, and strong charges for particles in the SU(5) model, rotated by the predicted weak mixing angle, showing electric charge roughly along the vertical. In addition to Standard Model particles, the theory includes twelve colored X bosons, responsible for proton decay.

SU(5) is the simplest GUT. The smallest simple Lie group which contains the standard model, and upon which the first Grand Unified Theory was based, is

${\displaystyle \mathrm{S}\mathrm{U}(5)\supset \mathrm{S}\mathrm{U}(3)\times \mathrm{S}\mathrm{U}(2)\times \mathrm{U}(1).}$

Such group symmetries allow the reinterpretation of several known particles, including the photon, W and Z bosons, and gluon, as different states of a single particle field. However, it is not obvious that the simplest possible choices for the extended "Grand Unified" symmetry should yield the correct inventory of elementary particles. The fact that all currently known matter particles fit perfectly into three copies of the smallest group representations of SU(5) and immediately carry the correct observed charges, is one of the first and most important reasons why people believe that a Grand Unified Theory might actually be realized in nature.

The two smallest irreducible representations of SU(5) are 5 (the defining representation) and 10. (These bold numbers indicate the dimension of the representation.) In the standard assignment, the 5 contains the charge conjugates of the right-handed down-type quark color triplet and a left-handed lepton isospin doublet, while the 10 contains the six up-type quark components, the left-handed down-type quark color triplet, and the right-handed electron. This scheme has to be replicated for each of the three known generations of matter. It is notable that the theory is anomaly free with this matter content.

The hypothetical right-handed neutrinos are a singlet of SU(5), which means its mass is not forbidden by any symmetry; it doesn't need a spontaneous electroweak symmetry breaking which explains why its mass would be heavy (see seesaw mechanism).

SO(10)

Main article: SO(10)

The pattern of weak isospin, W, weaker isospin, W′, strong g3 and g8, and baryon minus lepton, B, charges for particles in the SO(10) Grand Unified Theory, rotated to show the embedding in E₆.

The next simple Lie group which contains the standard model is

${\displaystyle \mathrm{S}\mathrm{O}(10)\supset \mathrm{S}\mathrm{U}(5)\supset \mathrm{S}\mathrm{U}(3)\times \mathrm{S}\mathrm{U}(2)\times \mathrm{U}(1).}$

Here, the unification of matter is even more complete, since the irreducible spinor representation 16 contains both the 5 and 10 of SU(5) and a right-handed neutrino, and thus the complete particle content of one generation of the extended standard model with neutrino masses. This is already the largest simple group that achieves the unification of matter in a scheme involving only the already known matter particles (apart from the Higgs sector).

Since different standard model fermions are grouped together in larger representations, GUTs specifically predict relations among the fermion masses, such as between the electron and the down quark, the muon and the strange quark, and the tau lepton and the bottom quark for SU(5) and SO(10). Some of these mass relations hold approximately, but most don't (see Georgi-Jarlskog mass relation).

The boson matrix for SO(10) is found by taking the 15 × 15 matrix from the 10 + 5 representation of SU(5) and adding an extra row and column for the right-handed neutrino. The bosons are found by adding a partner to each of the 20 charged bosons (2 right-handed W bosons, 6 massive charged gluons and 12 X/Y type bosons) and adding an extra heavy neutral Z-boson to make 5 neutral bosons in total. The boson matrix will have a boson or its new partner in each row and column. These pairs combine to create the familiar 16D Dirac spinor matrices of SO(10).

E₆

Main article: E6 (mathematics)

In some forms of string theory, including E₈ × E₈ heterotic string theory, the resultant four-dimensional theory after spontaneous compactification on a six-dimensional Calabi–Yau manifold resembles a GUT based on the group E₆. Notably E₆ is the only exceptional simple Lie group to have any complex representations, a requirement for a theory to contain chiral fermions (namely all weakly-interacting fermions). Hence the other four (G₂, F₄, E₇, and E₈) can't be the gauge group of a GUT.

Extended Grand Unified Theories

Non-chiral extensions of the Standard Model with vectorlike split-multiplet particle spectra which naturally appear in the higher SU(N) GUTs considerably modify the desert physics and lead to the realistic (string-scale) grand unification for conventional three quark-lepton families even without using supersymmetry (see below). On the other hand, due to a new missing VEV mechanism emerging in the supersymmetric SU(8) GUT the simultaneous solution to the gauge hierarchy (doublet-triplet splitting) problem and problem of unification of flavor can be argued.

GUTs with four families / generations, SU(8): Assuming 4 generations of fermions instead of 3 makes a total of 64 types of particles. These can be put into 64 = 8 + 56 representations of SU(8). This can be divided into SU(5) × SU(3)_F × U(1) which is the SU(5) theory together with some heavy bosons which act on the generation number.

GUTs with four families / generations, O(16): Again assuming 4 generations of fermions, the 128 particles and anti-particles can be put into a single spinor representation of O(16).

Symplectic groups and quaternion representations

Symplectic gauge groups could also be considered. For example, Sp(8) (which is called Sp(4) in the article symplectic group) has a representation in terms of 4 × 4 quaternion unitary matrices which has a 16 dimensional real representation and so might be considered as a candidate for a gauge group. Sp(8) has 32 charged bosons and 4 neutral bosons. Its subgroups include SU(4) so can at least contain the gluons and photon of SU(3) × U(1). Although it's probably not possible to have weak bosons acting on chiral fermions in this representation. A quaternion representation of the fermions might be:

${\displaystyle {\left[\begin{array}{c}e+i\overline{e}+jv+k\overline{v}\\ u_r+i{\overline{u}}_{\overline{\mathrm{r}}}+j{d}_{\mathrm{r}}+k{\overline{d}}_{\overline{\mathrm{r}}}\\ u_g+i{\overline{u}}_{\overline{\mathrm{g}}}+j{d}_{\mathrm{g}}+k{\overline{d}}_{\overline{\mathrm{g}}}\\ u_b+i{\overline{u}}_{\overline{\mathrm{b}}}+j{d}_{\mathrm{b}}+k{\overline{d}}_{\overline{\mathrm{b}}}\end{array}\right]}_{\mathrm{L}}}$

A further complication with quaternion representations of fermions is that there are two types of multiplication: left multiplication and right multiplication which must be taken into account. It turns out that including left and right-handed 4 × 4 quaternion matrices is equivalent to including a single right-multiplication by a unit quaternion which adds an extra SU(2) and so has an extra neutral boson and two more charged bosons. Thus the group of left- and right-handed 4 × 4 quaternion matrices is Sp(8) × SU(2) which does include the standard model bosons:

${\displaystyle \mathrm{S}\mathrm{U}(4,\mathbb{H}{)}_{\mathrm{L}}\times {\mathbb{H}}_{\mathrm{R}}=\mathrm{S}\mathrm{p}(8)\times \mathrm{S}\mathrm{U}(2)\supset \mathrm{S}\mathrm{U}(4)\times \mathrm{S}\mathrm{U}(2)\supset \mathrm{S}\mathrm{U}(3)\times \mathrm{S}\mathrm{U}(2)\times \mathrm{U}(1)}$

If ${\displaystyle \psi }$ is a quaternion valued spinor, ${\displaystyle A_{\mu }^{ab}}$ is quaternion hermitian 4 × 4 matrix coming from Sp(8) and ${\displaystyle B_{\mu }}$ is a pure vector quaternion (both of which are 4-vector bosons) then the interaction term is:

${\displaystyle \overline{{\psi }^a}{\gamma }_{\mu }\left(A_{\mu }^{ab}{\psi }^b+{\psi }^a{B}_{\mu }\right)}$

Octonion representations

It can be noted that a generation of 16 fermions can be put into the form of an octonion with each element of the octonion being an 8-vector. If the 3 generations are then put in a 3x3 hermitian matrix with certain additions for the diagonal elements then these matrices form an exceptional (Grassmann) Jordan algebra, which has the symmetry group of one of the exceptional Lie groups (F₄, E₆, E₇, or E₈) depending on the details.

${\displaystyle \psi =\left[\begin{array}{ccc}a& e& \mu \\ \overline{e}& b& \tau \\ \overline{\mu }& \overline{\tau }& c\end{array}\right]}$

${\displaystyle [{\psi }_A,{\psi }_B]\subset {\mathrm{J}}_3(\mathbb{O})}$

Because they are fermions the anti-commutators of the Jordan algebra become commutators. It is known that E₆ has subgroup O(10) and so is big enough to include the Standard Model. An E₈ gauge group, for example, would have 8 neutral bosons, 120 charged bosons and 120 charged anti-bosons. To account for the 248 fermions in the lowest multiplet of E₈, these would either have to include anti-particles (and so have baryogenesis), have new undiscovered particles, or have gravity-like (spin connection) bosons affecting elements of the particles spin direction. Each of these possesses theoretical problems.

Beyond Lie groups

Other structures have been suggested including Lie 3-algebras and Lie superalgebras. Neither of these fit with Yang–Mills theory. In particular Lie superalgebras would introduce bosons with incorrect statistics. Supersymmetry, however, does fit with Yang–Mills.

Unification of forces and the role of supersymmetry

The unification of forces is possible due to the energy scale dependence of force coupling parameters in quantum field theory called renormalization group "running", which allows parameters with vastly different values at usual energies to converge to a single value at a much higher energy scale.

The renormalization group running of the three gauge couplings in the Standard Model has been found to nearly, but not quite, meet at the same point if the hypercharge is normalized so that it is consistent with SU(5) or SO(10) GUTs, which are precisely the GUT groups which lead to a simple fermion unification. This is a significant result, as other Lie groups lead to different normalizations. However, if the supersymmetric extension MSSM is used instead of the Standard Model, the match becomes much more accurate. In this case, the coupling constants of the strong and electroweak interactions meet at the grand unification energy, also known as the GUT scale:

${\displaystyle {\mathrm{\Lambda }}_{\text{GUT}}\approx {10}^{16}\text{GeV}.}$

It is commonly believed that this matching is unlikely to be a coincidence, and is often quoted as one of the main motivations to further investigate supersymmetric theories despite the fact that no supersymmetric partner particles have been experimentally observed. Also, most model builders simply assume supersymmetry because it solves the hierarchy problem—i.e., it stabilizes the electroweak Higgs mass against radiative corrections.

Neutrino masses

Since Majorana masses of the right-handed neutrino are forbidden by SO(10) symmetry, SO(10) GUTs predict the Majorana masses of right-handed neutrinos to be close to the GUT scale where the symmetry is spontaneously broken in those models. In supersymmetric GUTs, this scale tends to be larger than would be desirable to obtain realistic masses of the light, mostly left-handed neutrinos (see neutrino oscillation) via the seesaw mechanism. These predictions are independent of the Georgi–Jarlskog mass relations, wherein some GUTs predict other fermion mass ratios.

Proposed theories

Several theories have been proposed, but none is currently universally accepted. An even more ambitious theory that includes all fundamental forces, including gravitation, is termed a theory of everything. Some common mainstream GUT models are:

• Pati–Salam model – SU(4) × SU(2) × SU(2)
• Georgi–Glashow model – SU(5); and Flipped SU(5) – SU(5) × U(1)
• SO(10) model; and Flipped SO(10) – SO(10) × U(1)
• E₆ model; and Trinification – SU(3) × SU(3) × SU(3)
• minimal left-right model – SU(3)_C × SU(2)_L × SU(2)_R × U(1)_B−L
• 331 model – SU(3)_C × SU(3)_L × U(1)_X
• chiral color

Not quite GUTs:

• Technicolor models
• Little Higgs
• String theory
• Causal fermion systems
• M-theory
• Preons
• Loop quantum gravity
• Causal dynamical triangulation theory

Note: These models refer to Lie algebras not to Lie groups. The Lie group could be ${\displaystyle [\mathrm{S}\mathrm{U}(4)\times \mathrm{S}\mathrm{U}(2)\times \mathrm{S}\mathrm{U}(2)]/{\mathbb{Z}}_2,}$ just to take a random example.

The most promising candidate is SO(10). (Minimal) SO(10) does not contain any exotic fermions (i.e. additional fermions besides the Standard Model fermions and the right-handed neutrino), and it unifies each generation into a single irreducible representation. A number of other GUT models are based upon subgroups of SO(10). They are the minimal left-right model, SU(5), flipped SU(5) and the Pati–Salam model. The GUT group E₆ contains SO(10), but models based upon it are significantly more complicated. The primary reason for studying E₆ models comes from E₈ × E₈ heterotic string theory.

GUT models generically predict the existence of topological defects such as monopoles, cosmic strings, domain walls, and others. But none have been observed. Their absence is known as the monopole problem in cosmology. Many GUT models also predict proton decay, although not the Pati–Salam model. As of now, proton decay has never been experimentally observed. The minimal experimental limit on the proton's lifetime pretty much rules out minimal SU(5) and heavily constrains the other models. The lack of detected supersymmetry to date also constrains many models.

Proton Decay. These graphics refer to the X boson and Higgs boson families.

• 
  Dimension 6 proton decay mediated by the X boson ${\displaystyle (3,2{)}_{-\frac{5}{6}}}$ in SU(5) GUT
• 
  Dimension 6 proton decay mediated by the X boson ${\displaystyle (3,2{)}_{\frac{1}{6}}}$ in flipped SU(5) GUT
• 
  Dimension 6 proton decay mediated by the triplet Higgs ${\displaystyle T(3,1{)}_{-\frac{1}{3}}}$ and the anti-triplet Higgs ${\displaystyle \overline{T}(\overline{3},1{)}_{\frac{1}{3}}}$ in SU(5) GUT

Some GUT theories like SU(5) and SO(10) suffer from what is called the doublet-triplet problem. These theories predict that for each electroweak Higgs doublet, there is a corresponding colored Higgs triplet field with a very small mass (many orders of magnitude smaller than the GUT scale here). In theory, unifying quarks with leptons, the Higgs doublet would also be unified with a Higgs triplet. Such triplets have not been observed. They would also cause extremely rapid proton decay (far below current experimental limits) and prevent the gauge coupling strengths from running together in the renormalization group.

Most GUT models require a threefold replication of the matter fields. As such, they do not explain why there are three generations of fermions. Most GUT models also fail to explain the little hierarchy between the fermion masses for different generations.

Ingredients

A GUT model consists of a gauge group which is a compact Lie group, a connection form for that Lie group, a Yang–Mills action for that connection given by an invariant symmetric bilinear form over its Lie algebra (which is specified by a coupling constant for each factor), a Higgs sector consisting of a number of scalar fields taking on values within real/complex representations of the Lie group and chiral Weyl fermions taking on values within a complex rep of the Lie group. The Lie group contains the Standard Model group and the Higgs fields acquire VEVs leading to a spontaneous symmetry breaking to the Standard Model. The Weyl fermions represent matter.

Current evidence

The discovery of neutrino oscillations indicates that the Standard Model is incomplete, but there is currently no clear evidence that nature is described by any Grand Unified Theory. Neutrino oscillations have led to renewed interest toward certain GUT such as SO(10).

One of the few possible experimental tests of certain GUT is proton decay and also fermion masses. There are a few more special tests for supersymmetric GUT. However, minimum proton lifetimes from research (at or exceeding the 10³⁴~10³⁵ year range) have ruled out simpler GUTs and most non-SUSY models.  The maximum upper limit on proton lifetime (if unstable), is calculated at 6×10³⁹ years for SUSY models and 1.4×10³⁶ years for minimal non-SUSY GUTs.

The gauge coupling strengths of QCD, the weak interaction and hypercharge seem to meet at a common length scale called the GUT scale and equal approximately to 10¹⁶ GeV (slightly less than the Planck energy of 10¹⁹ GeV), which is somewhat suggestive. This interesting numerical observation is called the gauge coupling unification, and it works particularly well if one assumes the existence of superpartners of the Standard Model particles. Still, it is possible to achieve the same by postulating, for instance, that ordinary (non supersymmetric) SO(10) models break with an intermediate gauge scale, such as the one of Pati–Salam group.