Thermohaline circulation

From Wikipedia, the free encyclopedia

 

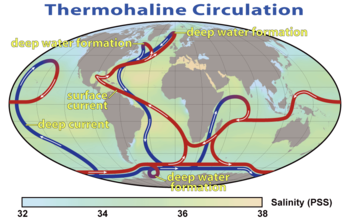
A summary of the path of the thermohaline circulation. Blue paths represent deep-water currents, while red paths represent surface currents.

Play media

Thermohaline circulation

Thermohaline circulation (THC) is a part of the large-scale ocean circulation that is driven by global density gradients created by surface heat and freshwater fluxes.^[1][2] The adjective thermohaline derives from thermo- referring to temperature and -haline referring to salt content, factors which together determine the density of sea water. Wind-driven surface currents (such as the Gulf Stream) travel polewards from the equatorial Atlantic Ocean, cooling en route, and eventually sinking at high latitudes (forming North Atlantic Deep Water). This dense water then flows into the ocean basins. While the bulk of it upwells in the Southern Ocean, the oldest waters (with a transit time of around 1000 years)^[3] upwell in the North Pacific.^[4] Extensive mixing therefore takes place between the ocean basins, reducing differences between them and making the Earth's oceans a global system. On their journey, the water masses transport both energy (in the form of heat) and matter (solids, dissolved substances and gases) around the globe. As such, the state of the circulation has a large impact on the climate of the Earth.

The thermohaline circulation is sometimes called the ocean conveyor belt, the great ocean conveyor, or the global conveyor belt. On occasion, it is used to refer to the meridional overturning circulation (often abbreviated as MOC). The term MOC is more accurate and well defined, as it is difficult to separate the part of the circulation which is driven by temperature and salinity alone as opposed to other factors such as the wind and tidal forces.^[5] Moreover, temperature and salinity gradients can also lead to circulation effects that are not included in the MOC itself.

Overview

The global conveyor belt on a continuous-ocean map

The movement of surface currents pushed by the wind is fairly intuitive. For example, the wind easily produces ripples on the surface of a pond. Thus the deep ocean—devoid of wind—was assumed to be perfectly static by early oceanographers. However, modern instrumentation shows that current velocities in deep water masses can be significant (although much less than surface speeds). In general, ocean water velocities range from fractions of centimeters per second (in the depth of the oceans) to sometimes more than 1 m/s in surface currents like the Gulf Stream and Kuroshio.

In the deep ocean, the predominant driving force is differences in density, caused by salinity and temperature variations (increasing salinity and lowering the temperature of a fluid both increase its density). There is often confusion over the components of the circulation that are wind and density driven.^[6][7] Note that ocean currents due to tides are also significant in many places; most prominent in relatively shallow coastal areas, tidal currents can also be significant in the deep ocean. There they are currently thought to facilitate mixing processes, especially diapycnal mixing.^[8]

The density of ocean water is not globally homogeneous, but varies significantly and discretely. Sharply defined boundaries exist between water masses which form at the surface, and subsequently maintain their own identity within the ocean. But these sharp boundaries are not to be imagined spatially but rather in a T-S-diagram where water masses are distinguished. They position themselves above or below each other according to their density, which depends on both temperature and salinity.

Warm seawater expands and is thus less dense than cooler seawater. Saltier water is denser than fresher water because the dissolved salts fill interstices between water molecules, resulting in more mass per unit volume. Lighter water masses float over denser ones (just as a piece of wood or ice will float on water, see buoyancy). This is known as "stable stratification" as opposed to unstable stratification (see Bruunt-Väisälä frequency) where denser waters are located over less dense waters (see convection or deep convection needed for water mass formation). When dense water masses are first formed, they are not stably stratified, so they seek to locate themselves in the correct vertical position according to their density. This motion is called convection, it orders the stratification by gravitation. Driven by the density gradients this sets up the main driving force behind deep ocean currents like the deep western boundary current (DWBC).

The thermohaline circulation is mainly driven by the formation of deep water masses in the North Atlantic and the Southern Ocean caused by differences in temperature and salinity of the water.
The great quantities of dense water sinking at high latitudes must be offset by equal quantities of water rising elsewhere. Note that cold water in polar zones sink relatively rapidly over a small area, while warm water in temperate and tropical zones rise more gradually across a much larger area. It then slowly returns poleward near the surface to repeat the cycle. The continual diffuse upwelling of deep water maintains the existence of the permanent thermocline found everywhere at low and mid-latitudes. This model was described by Henry Stommel and Arnold B. Arons in 1960 and is known as the Stommel-Arons box model for the MOC.^[9] This slow upward movement is approximated to be about 1 centimeter (0.5 inch) per day over most of the ocean. If this rise were to stop, downward movement of heat would cause the thermocline to descend and would reduce its steepness.

Formation of deep water masses

The dense water masses that sink into the deep basins are formed in quite specific areas of the North Atlantic and the Southern Ocean. In the North Atlantic, seawater at the surface of the ocean is intensely cooled by the wind and low ambient air temperatures. Wind moving over the water also produces a great deal of evaporation, leading to a decrease in temperature, called evaporative cooling related to latent heat. Evaporation removes only water molecules, resulting in an increase in the salinity of the seawater left behind, and thus an increase in the density of the water mass along with the decrease in temperature. In the Norwegian Sea evaporative cooling is predominant, and the sinking water mass, the North Atlantic Deep Water (NADW), fills the basin and spills southwards through crevasses in the submarine sills that connect Greenland, Iceland and Great Britain which are known as the Greenland-Scotland-Ridge. It then flows very slowly into the deep abyssal plains of the Atlantic, always in a southerly direction. Flow from the Arctic Ocean Basin into the Pacific, however, is blocked by the narrow shallows of the Bering Strait.

Diagram showing relation between temperature and salinity for sea water density maximum and sea water freezing temperature.

In the Southern Ocean, strong katabatic winds blowing from the Antarctic continent onto the ice shelves will blow the newly formed sea ice away, opening polynyas along the coast. The ocean, no longer protected by sea ice, suffers a brutal and strong cooling (see polynya). Meanwhile, sea ice starts reforming, so the surface waters also get saltier, hence very dense. In fact, the formation of sea ice contributes to an increase in surface seawater salinity; saltier brine is left behind as the sea ice forms around it (pure water preferentially being frozen). Increasing salinity lowers the freezing point of seawater, so cold liquid brine is formed in inclusions within a honeycomb of ice. The brine progressively melts the ice just beneath it, eventually dripping out of the ice matrix and sinking. This process is known as brine rejection.

The resulting Antarctic Bottom Water (AABW) sinks and flows north and east, but is so dense it actually underflows the NADW. AABW formed in the Weddell Sea will mainly fill the Atlantic and Indian Basins, whereas the AABW formed in the Ross Sea will flow towards the Pacific Ocean.

The dense water masses formed by these processes flow downhill at the bottom of the ocean, like a stream within the surrounding less dense fluid, and fill up the basins of the polar seas. Just as river valleys direct streams and rivers on the continents, the bottom topography constrains the deep and bottom water masses.

Note that, unlike fresh water, seawater does not have a density maximum at 4 °C but gets denser as it cools all the way to its freezing point of approximately −1.8 °C. This freezing point is however a function of salinity and pressure and thus -1.8°C is not a general freezing temperature for sea water (see diagram to the right).

Movement of deep water masses

Formation and movement of the deep water masses at the North Atlantic Ocean, creates sinking water masses that fill the basin and flows very slowly into the deep abyssal plains of the Atlantic. This high-latitude cooling and the low-latitude heating drives the movement of the deep water in a polar southward flow. The deep water flows through the Antarctic Ocean Basin around South Africa where it is split into two routes: one into the Indian Ocean and one past Australia into the Pacific.

At the Indian Ocean, some of the cold and salty water from the Atlantic—drawn by the flow of warmer and fresher upper ocean water from the tropical Pacific—causes a vertical exchange of dense, sinking water with lighter water above. It is known as overturning. In the Pacific Ocean, the rest of the cold and salty water from the Atlantic undergoes haline forcing, and becomes warmer and fresher more quickly.

The out-flowing undersea of cold and salty water makes the sea level of the Atlantic slightly lower than the Pacific and salinity or halinity of water at the Atlantic higher than the Pacific. This generates a large but slow flow of warmer and fresher upper ocean water from the tropical Pacific to the Indian Ocean through the Indonesian Archipelago to replace the cold and salty Antarctic Bottom Water. This is also known as 'haline forcing' (net high latitude freshwater gain and low latitude evaporation). This warmer, fresher water from the Pacific flows up through the South Atlantic to Greenland, where it cools off and undergoes evaporative cooling and sinks to the ocean floor, providing a continuous thermohaline circulation.^[10]

Hence, a recent and popular name for the thermohaline circulation, emphasizing the vertical nature and pole-to-pole character of this kind of ocean circulation, is the meridional overturning circulation.

Quantitative estimation

Direct estimates of the strength of the thermohaline circulation have been made at 26.5°N in the North Atlantic since 2004 by the UK-US RAPID programme.^[11] By combining direct estimates of ocean transport using current meters and subsea cable measurements with estimates of the geostrophic current from temperature and salinity measurements, the RAPID programme provides continuous, full-depth, basinwide estimates of the thermohaline circulation or, more accurately, the meridional overturning circulation.

The deep water masses that participate in the MOC have chemical, temperature and isotopic ratio signatures and can be traced, their flow rate calculated, and their age determined. These include ²³¹Pa / ²³⁰Th ratios.

Gulf Stream

Benjamin Franklin's map of the Gulf Stream

The Gulf Stream, together with its northern extension towards Europe, the North Atlantic Drift, is a powerful, warm, and swift Atlantic ocean current that originates at the tip of Florida, and follows the eastern coastlines of the United States and Newfoundland before crossing the Atlantic Ocean. The process of western intensification causes the Gulf Stream to be a northward accelerating current off the east coast of North America.^[12] At about 40°0′N 30°0′W, it splits in two, with the northern stream crossing to northern Europe and the southern stream recirculating off West Africa. The Gulf Stream influences the climate of the east coast of North America from Florida to Newfoundland, and the west coast of Europe. Although there has been recent debate, there is consensus that the climate of Western Europe and Northern Europe is warmer than it would otherwise be due to the North Atlantic drift,^[13][14] one of the branches from the tail of the Gulf Stream. It is part of the North Atlantic Gyre. Its presence has led to the development of strong cyclones of all types, both within the atmosphere and within the ocean. The Gulf Stream is also a significant potential source of renewable power generation.^[15][16]

Upwelling

All these dense water masses sinking into the ocean basins displace the older deep water masses were made less dense by ocean mixing. To maintain a balance, water must be rising elsewhere. However, because this thermohaline upwelling is so widespread and diffuse, its speeds are very slow even compared to the movement of the bottom water masses. It is therefore difficult to measure where upwelling occurs using current speeds, given all the other wind-driven processes going on in the surface ocean. Deep waters have their own chemical signature, formed from the breakdown of particulate matter falling into them over the course of their long journey at depth. A number of scientists have tried to use these tracers to infer where the upwelling occurs.
Wallace Broecker, using box models, has asserted that the bulk of deep upwelling occurs in the North Pacific, using as evidence the high values of silicon found in these waters. Other investigators have not found such clear evidence. Computer models of ocean circulation increasingly place most of the deep upwelling in the Southern Ocean,^[17] associated with the strong winds in the open latitudes between South America and Antarctica. While this picture is consistent with the global observational synthesis of William Schmitz at Woods Hole and with low observed values of diffusion, not all observational syntheses agree. Recent papers by Lynne Talley at the Scripps Institution of Oceanography and Bernadette Sloyan and Stephen Rintoul in Australia suggest that a significant amount of dense deep water must be transformed to light water somewhere north of the Southern Ocean.

Effects on global climate

The thermohaline circulation plays an important role in supplying heat to the polar regions, and thus in regulating the amount of sea ice in these regions, although poleward heat transport outside the tropics is considerably larger in the atmosphere than in the ocean.^[18] Changes in the thermohaline circulation are thought to have significant impacts on the Earth's radiation budget. Insofar as the thermohaline circulation governs the rate at which deep waters are exposed to the surface, it may also play an important role in the concentration of carbon dioxide in the atmosphere. While it is often stated that the thermohaline circulation is the primary reason that Western Europe is so temperate, it has been suggested that this is largely incorrect, and that Europe is warm mostly because it lies downwind of an ocean basin, and because of the effect of atmospheric waves bringing warm air north from the subtropics.^[19] However, the underlying assumptions of this particular analysis have likewise been challenged.^[20]

Large influxes of low-density meltwater from Lake Agassiz and deglaciation in North America are thought to have led to a shifting of deep water formation and subsidence in the extreme North Atlantic and caused the climate period in Europe known as the Younger Dryas.^[21]

Shutdown of thermohaline circulation

In 2005, British researchers noticed that the net flow of the northern Gulf Stream had decreased by about 30% since 1957. Coincidentally, scientists at Woods Hole had been measuring the freshening of the North Atlantic as Earth becomes warmer. Their findings suggested that precipitation increases in the high northern latitudes, and polar ice melts as a consequence. By flooding the northern seas with lots of extra fresh water, global warming could, in theory, divert the Gulf Stream waters that usually flow northward, past the British Isles and Norway, and cause them to instead circulate toward the equator. If this were to happen, Europe's climate would be seriously impacted.^[22][23][24]
Downturn of AMOC (Atlantic meridional overturning circulation), has been tied to extreme regional sea level rise.^[25]

In 2013, an unexpected significant weakening of the THC led to one of the quietest Atlantic hurricane seasons observed since 1994. The main cause of the inactivity was caused by a continuation of the spring pattern across the Atlantic basin.

Tidal force

From Wikipedia, the free encyclopedia

 

Figure 1: Comet Shoemaker-Levy 9 in 1994 after breaking up under the influence of Jupiter's tidal forces during a previous pass in 1992.

Play media

This simulation shows a star getting torn apart by the gravitational tides of a supermassive black hole.

The tidal force is a force that is the secondary effect of the force of gravity; it is responsible for the phenomenon of tides. It arises because the gravitational force exerted by one body on another is not constant across it: the nearest side is attracted more strongly than the farthest side. Thus, the tidal force is differential. Consider the gravitational attraction of the Moon on the oceans nearest to the Moon, the solid Earth and the oceans farthest from the Moon. There is a mutual attraction between the Moon and the solid Earth, which can be considered to act on its centre of mass. However, the near oceans are more strongly attracted and, especially since they are fluid, they approach the Moon slightly, causing a high tide. The far oceans are attracted less. The attraction on the far-side oceans could be expected to cause a low tide, but since the solid Earth is attracted (accelerated) more strongly towards the moon, there is a relative acceleration of those waters in the outwards direction. Viewing the Earth as a whole, we see that all its mass experiences a mutual attraction with that of the Moon, but the near oceans more so than the far oceans, leading to a separation of the two.

In a more general usage in celestial mechanics, the expression "tidal force" can refer to a situation in which a body or material (for example, tidal water) is mainly under the gravitational influence of a second body (for example, the Earth), but is also perturbed by the gravitational effects of a third body (for example, the Moon). The perturbing force is sometimes in such cases called a tidal force^[1] (for example, the perturbing force on the Moon): it is the difference between the force exerted by the third body on the second and the force exerted by the third body on the first.^[2]

Explanation

Figure 2: The Moon's gravity differential field at the surface of the Earth is known (along with another and weaker differential effect due to the Sun) as the Tide Generating Force. This is the primary mechanism driving tidal action, explaining two tidal equipotential bulges, and accounting for two high tides per day. In this figure, the Earth is the central blue circle while the Moon is far off to the right. The outward direction of the arrows on the right and left indicates that where the Moon is overhead (or at the nadir) its perturbing force opposes that between the earth and ocean.

When a body (body 1) is acted on by the gravity of another body (body 2), the field can vary significantly on body 1 between the side of the body facing body 2 and the side facing away from body 2. Figure 2 shows the differential force of gravity on a spherical body (body 1) exerted by another body (body 2). These so-called tidal forces cause strains on both bodies and may distort them or even, in extreme cases, break one or the other apart.^[3] The Roche limit is the distance from a planet at which tidal effects would cause an object to disintegrate because the differential force of gravity from the planet overcomes the attraction of the parts of the object for one another.^[4] These strains would not occur if the gravitational field were uniform, because a uniform field only causes the entire body to accelerate together in the same direction and at the same rate.

Effects of tidal forces

Figure 3: Saturn's rings are inside the orbits of its principal moons. Tidal forces oppose gravitational coalescence of the material in the rings to form moons.^[5]

In the case of an infinitesimally small elastic sphere, the effect of a tidal force is to distort the shape of the body without any change in volume. The sphere becomes an ellipsoid with two bulges, pointing towards and away from the other body. Larger objects distort into an ovoid, and are slightly compressed, which is what happens to the Earth's oceans under the action of the Moon. The Earth and Moon rotate about their common center of mass or barycenter, and their gravitational attraction provides the centripetal force necessary to maintain this motion. To an observer on the Earth, very close to this barycenter, the situation is one of the Earth as body 1 acted upon by the gravity of the Moon as body 2. All parts of the Earth are subject to the Moon's gravitational forces, causing the water in the oceans to redistribute, forming bulges on the sides near the Moon and far from the Moon.^[6]

When a body rotates while subject to tidal forces, internal friction results in the gradual dissipation of its rotational kinetic energy as heat. In the case for the Earth, and Earth's Moon, the loss of rotational kinetic energy results in a gain of about 2 milliseconds per century. If the body is close enough to its primary, this can result in a rotation which is tidally locked to the orbital motion, as in the case of the Earth's moon. Tidal heating produces dramatic volcanic effects on Jupiter's moon Io. Stresses caused by tidal forces also cause a regular monthly pattern of moonquakes on Earth's Moon.^[7]

Tidal forces contribute to ocean currents, which moderate global temperatures by transporting heat energy toward the poles. It has been suggested that in addition to other factors, harmonic beat variations in tidal forcing may contribute to climate changes. However, no strong link has been found to date.^[8]

Tidal effects become particularly pronounced near small bodies of high mass, such as neutron stars or black holes, where they are responsible for the "spaghettification" of infalling matter. Tidal forces create the oceanic tide of Earth's oceans, where the attracting bodies are the Moon and, to a lesser extent, the Sun. Tidal forces are also responsible for tidal locking, tidal acceleration, and tidal heating. Tides may also induce seismicity.

By generating conducting fluids within the interior of the Earth, tidal forces also affect the Earth's magnetic field.^[9]

Mathematical treatment

Tidal force is responsible for the merge of galactic pair MRK 1034.^[10]

Figure 4: Graphic of tidal forces. The top picture shows the gravity field of a body to the right, the lower shows their residual once the field at the centre of the sphere is subtracted; this is the tidal force. See Figure 2 for a more detailed version

For a given (externally generated) gravitational field, the tidal acceleration at a point with respect to a body is obtained by vectorially subtracting the gravitational acceleration at the center of the body (due to the given externally generated field) from the gravitational acceleration (due to the same field) at the given point. Correspondingly, the term tidal force is used to describe the forces due to tidal acceleration. Note that for these purposes the only gravitational field considered is the external one; the gravitational field of the body (as shown in the graphic) is not relevant. (In other words, the comparison is with the conditions at the given point as they would be if there were no externally generated field acting unequally at the given point and at the center of the reference body. The externally generated field is usually that produced by a perturbing third body, often the Sun or the Moon in the frequent example-cases of points on or above the Earth's surface in a geocentric reference frame.)

Tidal acceleration does not require rotation or orbiting bodies; for example, the body may be freefalling in a straight line under the influence of a gravitational field while still being influenced by (changing) tidal acceleration.

By Newton's law of universal gravitation and laws of motion, a body of mass m at distance R from the center of a sphere of mass M feels a force ${\displaystyle {\vec {F}}_{g}}$,

${\displaystyle {\vec {F}}_{g}=-{\hat {r}}~G~{\frac {Mm}{R^{2}}}}$

equivalent to an acceleration ${\displaystyle {\vec {a}}_{g}}$,

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}}$

where ${\displaystyle {\hat {r}}}$ is a unit vector pointing from the body M to the body m (here, acceleration from m towards M has negative sign).

Consider now the acceleration due to the sphere of mass M experienced by a particle in the vicinity of the body of mass m. With R as the distance from the center of M to the center of m, let ∆r be the (relatively small) distance of the particle from the center of the body of mass m. For simplicity, distances are first considered only in the direction pointing towards or away from the sphere of mass M. If the body of mass m is itself a sphere of radius ∆r, then the new particle considered may be located on its surface, at a distance (R ± ∆r) from the centre of the sphere of mass M, and ∆r may be taken as positive where the particle's distance from M is greater than R. Leaving aside whatever gravitational acceleration may be experienced by the particle towards m on account of m's own mass, we have the acceleration on the particle due to gravitational force towards M as:

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{(R\pm \Delta r)^{2}}}}$

Pulling out the R² term from the denominator gives:

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}~{\frac {1}{(1\pm \Delta r/R)^{2}}}}$

The Maclaurin series of ${\displaystyle 1/(1\pm x)^{2}}$ is ${\displaystyle 1\mp 2x+3x^{2}\mp \cdots }$ which gives a series expansion of:

${\displaystyle {\vec {a}}_{g}=-{\hat {r}}~G~{\frac {M}{R^{2}}}\pm {\hat {r}}~G~{\frac {2M}{R^{2}}}~{\frac {\Delta r}{R}}+\cdots }$

The first term is the gravitational acceleration due to M at the center of the reference body ${\displaystyle m}$, i.e., at the point where ${\displaystyle \Delta r}$ is zero. This term does not affect the observed acceleration of particles on the surface of m because with respect to M, m (and everything on its surface) is in free fall. When the force on the far particle is subtracted from the force on the near particle, this first term cancels, as do all other even-order terms. The remaining (residual) terms represent the difference mentioned above and are tidal force (acceleration) terms. When ∆r is small compared to R, the terms after the first residual term are very small and can be neglected, giving the approximate tidal acceleration ${\displaystyle {\vec {a}}_{t}}$(axial) for the distances ∆r considered, along the axis joining the centers of m and M:

${\displaystyle {\vec {a}}_{t}}$(axial) ${\displaystyle ~\approx ~\pm ~{\hat {r}}~2\Delta r~G~{\frac {M}{R^{3}}}}$

When calculated in this way for the case where ∆r is a distance along the axis joining the centers of m and M, ${\displaystyle {\vec {a}}_{t}}$ is directed outwards from to the center of m (where ∆r is zero).

Tidal accelerations can also be calculated away from the axis connecting the bodies m and M, requiring a vector calculation. In the plane perpendicular to that axis, the tidal acceleration is directed inwards (towards the center where ∆r is zero), and its magnitude is ${\displaystyle |{\vec {a}}_{t}}$(axial)${\displaystyle |/2}$ in linear approximation as in Figure 2.

The tidal accelerations at the surfaces of planets in the Solar System are generally very small. For example, the lunar tidal acceleration at the Earth's surface along the Moon-Earth axis is about 1.1 × 10⁻⁷ g, while the solar tidal acceleration at the Earth's surface along the Sun-Earth axis is about 0.52 × 10⁻⁷ g, where g is the gravitational acceleration at the Earth's surface. Hence the tide-raising force (acceleration) due to the Sun is about 45% of that due to the Moon.^[11] The solar tidal acceleration at the Earth's surface was first given by Newton in the Principia.^[12]

Valence bond theory

From Wikipedia, the free encyclopedia

In chemistry, valence bond (VB) theory is one of two basic theories, along with molecular orbital (MO) theory, that were developed to use the methods of quantum mechanics to explain chemical bonding. It focuses on how the atomic orbitals of the dissociated atoms combine to give individual chemical bonds when a molecule is formed. In contrast, molecular orbital theory has orbitals that cover the whole molecule.^[1]

History

In 1916, G. N. Lewis proposed that a chemical bond forms by the interaction of two shared bonding electrons, with the representation of molecules as Lewis structures. In 1927 the Heitler–London theory was formulated which for the first time enabled the calculation of bonding properties of the hydrogen molecule H₂ based on quantum mechanical considerations. Specifically, Walter Heitler determined how to use Schrödinger's wave equation (1926) to show how two hydrogen atom wavefunctions join together, with plus, minus, and exchange terms, to form a covalent bond. He then called up his associate Fritz London and they worked out the details of the theory over the course of the night.^[2] Later, Linus Pauling used the pair bonding ideas of Lewis together with Heitler–London theory to develop two other key concepts in VB theory: resonance (1928) and orbital hybridization (1930). According to Charles Coulson, author of the noted 1952 book Valence, this period marks the start of "modern valence bond theory", as contrasted with older valence bond theories, which are essentially electronic theories of valence couched in pre-wave-mechanical terms. Resonance theory was criticized as imperfect by Soviet chemists during the 1950s.^[3]

Theory

According to this theory a covalent bond is formed between the two atoms by the overlap of half filled valence atomic orbitals of each atom containing one unpaired electron. A valence bond structure is similar to a Lewis structure, but where a single Lewis structure cannot be written, several valence bond structures are used. Each of these VB structures represents a specific Lewis structure. This combination of valence bond structures is the main point of resonance theory. Valence bond theory considers that the overlapping atomic orbitals of the participating atoms form a chemical bond. Because of the overlapping, it is most probable that electrons should be in the bond region. Valence bond theory views bonds as weakly coupled orbitals (small overlap). Valence bond theory is typically easier to employ in ground state molecules. The inner-shell orbitals and electrons remain essentially unchanged during the formation of bonds.

σ bond between two atoms: localization of electron density

Two p-orbitals forming a π-bond.

The overlapping atomic orbitals can differ. The two types of overlapping orbitals are sigma and pi. Sigma bonds occur when the orbitals of two shared electrons overlap head-to-head. Pi bonds occur when two orbitals overlap when they are parallel. For example, a bond between two s-orbital electrons is a sigma bond, because two spheres are always coaxial. In terms of bond order, single bonds have one sigma bond, double bonds consist of one sigma bond and one pi bond, and triple bonds contain one sigma bond and two pi bonds. However, the atomic orbitals for bonding may be hybrids. Often, the bonding atomic orbitals have a character of several possible types of orbitals. The methods to get an atomic orbital with the proper character for the bonding is called hybridization.

Valence bond theory today

Modern valence bond theory now complements molecular orbital theory, which does not adhere to the valence bond idea that electron pairs are localized between two specific atoms in a molecule but that they are distributed in sets of molecular orbitals which can extend over the entire molecule. Molecular orbital theory can predict magnetic and ionization properties in a straightforward manner, while valence bond theory gives similar results but is more complicated. Modern valence bond theory views aromatic properties of molecules as due to spin coupling of the π orbitals.^[4][5][6][7] This is essentially still the old idea of resonance between Kekulé and Dewar structures. In contrast, molecular orbital theory views aromaticity as delocalization of the π-electrons. Valence bond treatments are restricted to relatively small molecules, largely due to the lack of orthogonality between valence bond orbitals and between valence bond structures, while molecular orbitals are orthogonal. On the other hand, valence bond theory provides a much more accurate picture of the reorganization of electronic charge that takes place when bonds are broken and formed during the course of a chemical reaction. In particular, valence bond theory correctly predicts the dissociation of homonuclear diatomic molecules into separate atoms, while simple molecular orbital theory predicts dissociation into a mixture of atoms and ions. For example, the molecular orbital function for dihydrogen is an equal mixture of the covalent and ionic valence bond structures and so predicts incorrectly that the molecule would dissociate into an equal mixture of hydrogen atoms and hydrogen positive and negative ions.

Modern valence bond theory replaces the overlapping atomic orbitals by overlapping valence bond orbitals that are expanded over a large number of basis functions, either centered each on one atom to give a classical valence bond picture, or centered on all atoms in the molecule. The resulting energies are more competitive with energies from calculations where electron correlation is introduced based on a Hartree–Fock reference wavefunction. The most recent text is by Shaik and Hiberty.^[8]

Applications of valence bond theory

An important aspect of the VB theory is the condition of maximum overlap, which leads to the formation of the strongest possible bonds. This theory is used to explain the covalent bond formation in many molecules.

For example, in the case of the F₂ molecule, the F−F bond is formed by the overlap of p_z orbitals of the two F atoms, each containing an unpaired electron. Since the nature of the overlapping orbitals are different in H₂ and F₂ molecules, the bond strength and bond lengths differ between H₂ and F₂ molecules.

In an HF molecule the covalent bond is formed by the overlap of the 1s orbital of H and the 2p_z orbital of F, each containing an unpaired electron. Mutual sharing of electrons between H and F results in a covalent bond in HF.

Electronegativity

From Wikipedia, the free encyclopedia

Electrostatic potential map of a water molecule, where the oxygen atom has a more negative charge (red) than the positive (blue) hydrogen atoms

Electronegativity, symbol χ, is a chemical property that describes the tendency of an atom to attract electrons (or electron density) towards itself.^[1] An atom's electronegativity is affected by both its atomic number and the distance at which its valence electrons reside from the charged nucleus. The higher the associated electronegativity number, the more an element or compound attracts electrons towards it.

The term "electronegativity" was introduced by Jöns Jacob Berzelius in 1811,^[2] though the concept was known even before that and was studied by many chemists including Avogadro.^[2] In spite of its long history, an accurate scale of electronegativity had to wait until 1932, when Linus Pauling proposed an electronegativity scale, which depends on bond energies, as a development of valence bond theory.^[3] It has been shown to correlate with a number of other chemical properties. Electronegativity cannot be directly measured and must be calculated from other atomic or molecular properties. Several methods of calculation have been proposed, and although there may be small differences in the numerical values of the electronegativity, all methods show the same periodic trends between elements.

The most commonly used method of calculation is that originally proposed by Linus Pauling. This gives a dimensionless quantity, commonly referred to as the Pauling scale (χ_r), on a relative scale running from around 0.7 to 3.98 (hydrogen = 2.20). When other methods of calculation are used, it is conventional (although not obligatory) to quote the results on a scale that covers the same range of numerical values: this is known as an electronegativity in Pauling units.

As it is usually calculated, electronegativity is not a property of an atom alone, but rather a property of an atom in a molecule.^[4] Properties of a free atom include ionization energy and electron affinity. It is to be expected that the electronegativity of an element will vary with its chemical environment,^[5] but it is usually considered to be a transferable property, that is to say that similar values will be valid in a variety of situations.

On the most basic level, electronegativity is determined by factors like the nuclear charge (the more protons an atom has, the more "pull" it will have on electrons) and the number/location of other electrons present in the atomic shells (the more electrons an atom has, the farther from the nucleus the valence electrons will be, and as a result the less positive charge they will experience—both because of their increased distance from the nucleus, and because the other electrons in the lower energy core orbitals will act to shield the valence electrons from the positively charged nucleus).

The opposite of electronegativity is electropositivity: a measure of an element's ability to donate electrons.

Caesium is the least electronegative element in the periodic table (=0.79), while fluorine is most electronegative (=3.98). Francium and caesium were originally both assigned 0.7; caesium's value was later refined to 0.79, but no experimental data allows a similar refinement for francium. However, francium's ionization energy is known to be slightly higher than caesium's, in accordance with the relativistic stabilization of the 7s orbital, and this in turn implies that francium is in fact more electronegative than caesium.^[6]

Electronegativities of the elements

v t e Periodic table of electronegativity by Pauling scale
→ Atomic radius decreases → Ionization energy increases → Electronegativity increases →
	1	2	3		4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Group →
↓ Period
1	H 2.20																		He
2	Li 0.98	Be 1.57												B 2.04	C 2.55	N 3.04	O 3.44	F 3.98	Ne
3	Na 0.93	Mg 1.31												Al 1.61	Si 1.90	P 2.19	S 2.58	Cl 3.16	Ar
4	K 0.82	Ca 1.00	Sc 1.36		Ti 1.54	V 1.63	Cr 1.66	Mn 1.55	Fe 1.83	Co 1.88	Ni 1.91	Cu 1.90	Zn 1.65	Ga 1.81	Ge 2.01	As 2.18	Se 2.55	Br 2.96	Kr 3.00
5	Rb 0.82	Sr 0.95	Y 1.22		Zr 1.33	Nb 1.6	Mo 2.16	Tc 1.9	Ru 2.2	Rh 2.28	Pd 2.20	Ag 1.93	Cd 1.69	In 1.78	Sn 1.96	Sb 2.05	Te 2.1	I 2.66	Xe 2.60
6	Cs 0.79	Ba 0.89	La 1.1		Hf 1.3	Ta 1.5	W 2.36	Re 1.9	Os 2.2	Ir 2.20	Pt 2.28	Au 2.54	Hg 2.00	Tl 1.62	Pb 1.87	Bi 2.02	Po 2.0	At 2.2	Rn 2.2
7	Fr 0.7[en 1]	Ra 0.9	Ac 1.1		Rf	Db	Sg	Bh	Hs	Mt	Ds	Rg	Cn	Nh	Fl	Mc	Lv	Ts	Og
					Ce 1.12	Pr 1.13	Nd 1.14	Pm 1.13	Sm 1.17	Eu 1.2	Gd 1.2	Tb 1.1	Dy 1.22	Ho 1.23	Er 1.24	Tm 1.25	Yb 1.1	Lu 1.27
					Th 1.3	Pa 1.5	U 1.38	Np 1.36	Pu 1.28	Am 1.13	Cm 1.28	Bk 1.3	Cf 1.3	Es 1.3	Fm 1.3	Md 1.3	No 1.3	Lr 1.3[en 2]
Values are given for the elements in their most common and stable oxidation states. See also: Electronegativities of the elements (data page)

Electronegativity of francium was chosen by Pauling as 0.7, close to that of caesium (also assessed 0.7 at that point). The base value of hydrogen was later increased by 0.10 and caesium's electronegativity was later refined to 0.79; however, no refinements have been made for francium as no experiment has been conducted and the old value was kept. However, francium is expected and, to a small extent, observed to be more electronegative than caesium. See francium for details.

See Brown, Geoffrey (2012). The Inaccessible Earth: An integrated view to its structure and composition. Springer Science & Business Media. p. 88. ISBN 9789401115162.

Methods of calculation

Pauling electronegativity

Pauling first proposed^[3] the concept of electronegativity in 1932 as an explanation of the fact that the covalent bond between two different atoms (A–B) is stronger than would be expected by taking the average of the strengths of the A–A and B–B bonds. According to valence bond theory, of which Pauling was a notable proponent, this "additional stabilization" of the heteronuclear bond is due to the contribution of ionic canonical forms to the bonding.

The difference in electronegativity between atoms A and B is given by:

${\displaystyle |\chi _{\rm {A}}-\chi _{\rm {B}}|=({\rm {eV}})^{-1/2}{\sqrt {E_{\rm {d}}({\rm {AB}})-[E_{\rm {d}}({\rm {AA}})+E_{\rm {d}}({\rm {BB}})]/2}}}$

where the dissociation energies, E_d, of the A–B, A–A and B–B bonds are expressed in electronvolts, the factor (eV)^{− 1⁄₂} being included to ensure a dimensionless result. Hence, the difference in Pauling electronegativity between hydrogen and bromine is 0.73 (dissociation energies: H–Br, 3.79 eV; H–H, 4.52 eV; Br–Br 2.00 eV)

As only differences in electronegativity are defined, it is necessary to choose an arbitrary reference point in order to construct a scale. Hydrogen was chosen as the reference, as it forms covalent bonds with a large variety of elements: its electronegativity was fixed first^[3] at 2.1, later revised^[7] to 2.20. It is also necessary to decide which of the two elements is the more electronegative (equivalent to choosing one of the two possible signs for the square root). This is usually done using "chemical intuition": in the above example, hydrogen bromide dissolves in water to form H⁺ and Br⁻ ions, so it may be assumed that bromine is more electronegative than hydrogen. However, in principle, since the same electronegativities should be obtained for any two bonding compounds, the data are in fact overdetermined, and the signs are unique once a reference point is fixed (usually, for H or F).

To calculate Pauling electronegativity for an element, it is necessary to have data on the dissociation energies of at least two types of covalent bond formed by that element. A. L. Allred updated Pauling's original values in 1961 to take account of the greater availability of thermodynamic data,^[7] and it is these "revised Pauling" values of the electronegativity that are most often used.

The essential point of Pauling electronegativity is that there is an underlying, quite accurate, semi-empirical formula for dissociation energies, namely:

${\displaystyle E_{\rm {d}}({\rm {AB}})=[E_{\rm {d}}({\rm {AA}})+E_{\rm {d}}({\rm {BB}})]/2+(\chi _{\rm {A}}-\chi _{\rm {B}})^{2}eV}$

or sometimes, a more accurate fit

${\displaystyle E_{\rm {d}}({\rm {AB}})={\sqrt {E_{\rm {d}}({\rm {AA}})E_{\rm {d}}({\rm {BB}})}}+1.3(\chi _{\rm {A}}-\chi _{\rm {B}})^{2}eV}$

This is an approximate equation, but holds with good accuracy. Pauling obtained it by noting that a bond can be approximately represented as a quantum mechanical superposition of a covalent bond and two ionic bond-states. The covalent energy of a bond is approximately, by quantum mechanical calculations, the geometric mean of the two energies of covalent bonds of the same molecules, and there is an additional energy that comes from ionic factors, i.e. polar character of the bond.

The geometric mean is approximately equal to the arithmetic mean - which is applied in the first formula above - when the energies are of the similar value, e.g., except for the highly electropositive elements, where there is a larger difference of two dissociation energies; the geometric mean is more accurate and almost always gives a positive excess energy, due to ionic bonding. The square root of this excess energy, Pauling notes, is approximately additive, and hence one can introduce the electronegativity. Thus, it is this semi-empirical formula for bond energy that underlies Pauling electronegativity concept.

The formulas are approximate, but this rough approximation is in fact relatively good and gives the right intuition, with the notion of polarity of the bond and some theoretical grounding in quantum mechanics. The electronegativities are then determined to best fit the data.

In more complex compounds, there is additional error since electronegativity depends on the molecular environment of an atom. Also, the energy estimate can be only used for single, not for multiple bonds. The energy of formation of a molecule containing only single bonds then can be approximated from an electronegativity table, and depends on the constituents and sum of squares of differences of electronegativities of all pairs of bonded atoms. Such a formula for estimating energy typically has relative error of order of 10%, but can be used to get a rough qualitative idea and understanding of a molecule.

Mulliken electronegativity

The correlation between Mulliken electronegativities (x-axis, in kJ/mol) and Pauling electronegativities (y-axis).

Robert S. Mulliken proposed that the arithmetic mean of the first ionization energy (E_i) and the electron affinity (E_ea) should be a measure of the tendency of an atom to attract electrons.^[8][9] As this definition is not dependent on an arbitrary relative scale, it has also been termed absolute electronegativity,^[10] with the units of kilojoules per mole or electronvolts.

${\displaystyle \chi =(E_{\rm {i}}+E_{\rm {ea}})/2\,}$

However, it is more usual to use a linear transformation to transform these absolute values into values that resemble the more familiar Pauling values. For ionization energies and electron affinities in electronvolts,^[11]

${\displaystyle \chi =0.187(E_{\rm {i}}+E_{\rm {ea}})+0.17\,}$

and for energies in kilojoules per mole,^[12]

${\displaystyle \chi =(1.97\times 10^{-3})(E_{\rm {i}}+E_{\rm {ea}})+0.19.}$

The Mulliken electronegativity can only be calculated for an element for which the electron affinity is known, fifty-seven elements as of 2006. The Mulliken electronegativity of an atom is sometimes said to be the negative of the chemical potential. By inserting the energetic definitions of the ionization potential and electron affinity into the Mulliken electronegativity, it is possible to show that the Mulliken chemical potential is a finite difference approximation of the electronic energy with respect to the number of electrons., i.e.,

${\displaystyle \mu ({\rm {Mulliken)=-\chi ({\rm {Mulliken)=-(E_{\rm {i}}+E_{\rm {ea}})/2\,}}}}}$

Allred–Rochow electronegativity

The correlation between Allred–Rochow electronegativities (x-axis, in Å⁻²) and Pauling electronegativities (y-axis).

A. Louis Allred and Eugene G. Rochow considered^[13] that electronegativity should be related to the charge experienced by an electron on the "surface" of an atom: The higher the charge per unit area of atomic surface the greater the tendency of that atom to attract electrons. The effective nuclear charge, Z_eff, experienced by valence electrons can be estimated using Slater's rules, while the surface area of an atom in a molecule can be taken to be proportional to the square of the covalent radius, r_cov. When r_cov is expressed in picometres,^[14]

${\displaystyle \chi =3590{{Z_{\rm {eff}}} \over {r_{\rm {cov}}^{2}}}+0.744}$

Sanderson electronegativity equalization

The correlation between Sanderson electronegativities (x-axis, arbitrary units) and Pauling electronegativities (y-axis).

R.T. Sanderson has also noted the relationship between Mulliken electronegativity and atomic size, and has proposed a method of calculation based on the reciprocal of the atomic volume.^[15] With a knowledge of bond lengths, Sanderson's model allows the estimation of bond energies in a wide range of compounds.^[16] Sanderson's model has also been used to calculate molecular geometry, s-electrons energy, NMR spin-spin constants and other parameters for organic compounds.^[17][18] This work underlies the concept of electronegativity equalization, which suggests that electrons distribute themselves around a molecule to minimize or to equalize the Mulliken electronegativity.^[19] This behavior is analogous to the equalization of chemical potential in macroscopic thermodynamics.^[20]

Allen electronegativity

The correlation between Allen electronegativities (x-axis, in kJ/mol) and Pauling electronegativities (y-axis).

Perhaps the simplest definition of electronegativity is that of Leland C. Allen, who has proposed that it is related to the average energy of the valence electrons in a free atom,^[21] ,^[22] ,^[23]

${\displaystyle \chi ={n_{\rm {s}}\varepsilon _{\rm {s}}+n_{\rm {p}}\varepsilon _{\rm {p}} \over n_{\rm {s}}+n_{\rm {p}}}}$

where ε_s,p are the one-electron energies of s- and p-electrons in the free atom and n_s,p are the number of s- and p-electrons in the valence shell. It is usual to apply a scaling factor, 1.75×10⁻³ for energies expressed in kilojoules per mole or 0.169 for energies measured in electronvolts, to give values that are numerically similar to Pauling electronegativities.

The one-electron energies can be determined directly from spectroscopic data, and so electronegativities calculated by this method are sometimes referred to as spectroscopic electronegativities. The necessary data are available for almost all elements, and this method allows the estimation of electronegativities for elements that cannot be treated by the other methods, e.g. francium, which has an Allen electronegativity of 0.67.^[24] However, it is not clear what should be considered to be valence electrons for the d- and f-block elements, which leads to an ambiguity for their electronegativities calculated by the Allen method.

In this scale neon has the highest electronegativity of all elements, followed by fluorine, helium, and oxygen.

v t e Electronegativity using the Allen scale
Group →	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
↓ Period
1	H 2.300																	He 4.160
2	Li 0.912	Be 1.576											B 2.051	C 2.544	N 3.066	O 3.610	F 4.193	Ne 4.787
3	Na 0.869	Mg 1.293											Al 1.613	Si 1.916	P 2.253	S 2.589	Cl 2.869	Ar 3.242
4	K 0.734	Ca 1.034	Sc 1.19	Ti 1.38	V 1.53	Cr 1.65	Mn 1.75	Fe 1.80	Co 1.84	Ni 1.88	Cu 1.85	Zn 1.59	Ga 1.756	Ge 1.994	As 2.211	Se 2.424	Br 2.685	Kr 2.966
5	Rb 0.706	Sr 0.963	Y 1.12	Zr 1.32	Nb 1.41	Mo 1.47	Tc 1.51	Ru 1.54	Rh 1.56	Pd 1.58	Ag 1.87	Cd 1.52	In 1.656	Sn 1.824	Sb 1.984	Te 2.158	I 2.359	Xe 2.582
6	Cs 0.659	Ba 0.881	Lu 1.09	Hf 1.16	Ta 1.34	W 1.47	Re 1.60	Os 1.65	Ir 1.68	Pt 1.72	Au 1.92	Hg 1.76	Tl 1.789	Pb 1.854	Bi 2.01	Po 2.19	At 2.39	Rn 2.60
7	Fr 0.67	Ra 0.89

Correlation of electronegativity with other properties

The variation of the isomer shift (y-axis, in mm/s) of [SnX₆]²⁻ anions, as measured by ¹¹⁹Sn Mössbauer spectroscopy, against the sum of the Pauling electronegativities of the halide substituents (x-axis).

The wide variety of methods of calculation of electronegativities, which all give results that correlate well with one another, is one indication of the number of chemical properties which might be affected by electronegativity. The most obvious application of electronegativities is in the discussion of bond polarity, for which the concept was introduced by Pauling. In general, the greater the difference in electronegativity between two atoms the more polar the bond that will be formed between them, with the atom having the higher electronegativity being at the negative end of the dipole. Pauling proposed an equation to relate "ionic character" of a bond to the difference in electronegativity of the two atoms,^[4] although this has fallen somewhat into disuse.

Several correlations have been shown between infrared stretching frequencies of certain bonds and the electronegativities of the atoms involved:^[25] however, this is not surprising as such stretching frequencies depend in part on bond strength, which enters into the calculation of Pauling electronegativities. More convincing are the correlations between electronegativity and chemical shifts in NMR spectroscopy^[26] or isomer shifts in Mössbauer spectroscopy^[27] (see figure). Both these measurements depend on the s-electron density at the nucleus, and so are a good indication that the different measures of electronegativity really are describing "the ability of an atom in a molecule to attract electrons to itself".^[1][4]

Trends in electronegativity

Periodic trends

The variation of Pauling electronegativity (y-axis) as one descends the main groups of the periodic table from the second period to the sixth period

In general, electronegativity increases on passing from left to right along a period, and decreases on descending a group. Hence, fluorine is the most electronegative of the elements (not counting noble gases), whereas caesium is the least electronegative, at least of those elements for which substantial data is available.^[24] This would lead one to believe that caesium fluoride is the compound whose bonding features the most ionic character.

There are some exceptions to this general rule. Gallium and germanium have higher electronegativities than aluminium and silicon, respectively, because of the d-block contraction. Elements of the fourth period immediately after the first row of the transition metals have unusually small atomic radii because the 3d-electrons are not effective at shielding the increased nuclear charge, and smaller atomic size correlates with higher electronegativity (see Allred-Rochow electronegativity, Sanderson electronegativity above). The anomalously high electronegativity of lead, in particular when compared to thallium and bismuth, appears to be an artifact of data selection (and data availability)—methods of calculation other than the Pauling method show the normal periodic trends for these elements.

Variation of electronegativity with oxidation number

In inorganic chemistry it is common to consider a single value of the electronegativity to be valid for most "normal" situations. While this approach has the advantage of simplicity, it is clear that the electronegativity of an element is not an invariable atomic property and, in particular, increases with the oxidation state of the element.

Allred used the Pauling method to calculate separate electronegativities for different oxidation states of the handful of elements (including tin and lead) for which sufficient data was available.^[7] However, for most elements, there are not enough different covalent compounds for which bond dissociation energies are known to make this approach feasible. This is particularly true of the transition elements, where quoted electronegativity values are usually, of necessity, averages over several different oxidation states and where trends in electronegativity are harder to see as a result.

Acid	Formula	Chlorine oxidation state	pKa
Hypochlorous acid	HClO	+1	+7.5
Chlorous acid	HClO2	+3	+2.0
Chloric acid	HClO3	+5	–1.0
Perchloric acid	HClO4	+7	–10

The chemical effects of this increase in electronegativity can be seen both in the structures of oxides and halides and in the acidity of oxides and oxoacids. Hence CrO₃ and Mn₂O₇ are acidic oxides with low melting points, while Cr₂O₃ is amphoteric and Mn₂O₃ is a completely basic oxide.

The effect can also be clearly seen in the dissociation constants of the oxoacids of chlorine. The effect is much larger than could be explained by the negative charge being shared among a larger number of oxygen atoms, which would lead to a difference in pK_a of log₁₀( ¹⁄₄) = –0.6 between hypochlorous acid and perchloric acid. As the oxidation state of the central chlorine atom increases, more electron density is drawn from the oxygen atoms onto the chlorine, reducing the partial negative charge on the oxygen atoms and increasing the acidity.

Group electronegativity

In organic chemistry, electronegativity is associated more with different functional groups than with individual atoms. The terms group electronegativity and substituent electronegativity are used synonymously. However, it is common to distinguish between the inductive effect and the resonance effect, which might be described as σ- and π-electronegativities, respectively. There are a number of linear free-energy relationships that have been used to quantify these effects, of which the Hammett equation is the best known. Kabachnik parameters are group electronegativities for use in organophosphorus chemistry.

Electropositivity

Electropositivity is a measure of an element's ability to donate electrons, and therefore form positive ions; thus, it is opposed to electronegativity.

Mainly, this is an attribute of metals, meaning that, in general, the greater the metallic character of an element the greater the electropositivity. Therefore, the alkali metals are most electropositive of all. This is because they have a single electron in their outer shell and, as this is relatively far from the nucleus of the atom, it is easily lost; in other words, these metals have low ionization energies.^[28]

While electronegativity increases along periods in the periodic table, and decreases down groups, electropositivity decreases along periods (from left to right) and increases down groups.