Adam Smith's Word

The notion that capitalism (which should be called the free market system) is based on glorifying greed is an old canard, and a dangerous one. It is simply the recognition that, if you give people individual liberty ("the right to life, liberty, and the pursuit of happiness") they will tend to act in the best interests of themselves and those/what they care about; and given that this is the strongest motivation of all humans possess, the greatest economic good for the greatest number will follow. As Adam Smith is famously quoted, "It is not from the benevolence of the butcher, the brewer, or the baker, that we can expect our dinner, but from their regard to their own interest." And in case you think Smith only meant material acquisition only, he also said, "How selfish soever man may be supposed, there are evidently some principles in his nature, which interest him in the fortune of others, and render their happiness necessary to him, though he derives nothing from it except the pleasure of seeing it."

---

Original link:  https://www.economist.com/blogs/freeexchange/2013/11/economic-history

Nov 1st 2013

by C.W. | LONDON

ADAM SMITH is known as the father of economics. Most people think of him as the archetypal free-marketeer. But Smith is often misquoted. This post will give a few examples of how people have misinterpreted Smith’s ideas—and show what he really meant. 

Smith sowed the seeds of his own problems. He tended to write pithy soundbites that left his ideas open to distortion. One of his best-known quips:

"It is not from the benevolence of the butcher, the brewer, or the baker, that we can expect our dinner, but from their regard to their own interest."

Journalists and economists frequently use this quotation. Most people think that Smith was advocating pure egoism. In fact, according to Athol Fitzgibbons, an economic historian, the reader can only understand the quotation within the context of the passage. And deeper analysis shows that Smith was making a subtle point, rather than advocating pure selfishness.

In the "Theory of Moral Sentiments", his second most famous book, Smith discusses the position of philosophers in society. He argues that it would be contradictory and unjust for them just to think about their self-interest. Instead philosophers needed to cultivate a sense of public duty in order to be any good at helping to solve the world’s most pressing problems. But butchers, brewers and bakers did not need such lofty aspirations—unlike philosophers, they could probably do their job well by acting selfishly. So according to Mr Fitzgibbons, when Smith mentions "their own interest", he is arguing that “not all occupations are pursued with the same low motive in mind”. Smith certainly did not intend to suggest that self-interest was the only driving force of human behaviour. 

And other evidence suggests that Smith had a more complex view of human action than most people give him credit for. This quotation appears on the very first page of the "Theory of Moral Sentiments":

How selfish soever man may be supposed, there are evidently some principles in his nature, which interest him in the fortune of others, and render their happiness necessary to him, though he derives nothing from it except the pleasure of seeing it.

Smith voices similar opinions when he mentions the “invisible hand”. The metaphor is used today for the idea that selfish individuals, operating independently, will bring about the best possible outcome. But this is a misinterpretation of Smith. The phrase "invisible hand" is used only three times (here, here and here) in Smith’s works. And according to Emma Rothschild, an expert on 18th century economic thought, its use was “ironical on each of the three occasions".

So much for selfishness. Smith’s ideas of the division of labour were revolutionary, says Tony Aspromourgos of Sydney University. Smith opens the "Wealth of Nations", his most famous book, with a discussion of a pin factory: 

[T]en persons [...] could make among them upwards of forty-eight thousand pins in a day…But if they had all wrought separately and independently [...] they certainly could not each of them have made twenty, perhaps not one pin in a day.

He reckoned that the “proper division and combination of [...] different operations” was a sure-fire way to business success. 

But Smith did not obsess over economic efficiency, as we have argued in another blog post. In fact, he thought that the division of labour could have negative effects—both for the individual and for society. In a later part of the "Wealth of Nations", Smith reckons that as a result of strict labour specialisation, the worker “has no occasion to exert his understanding or to exercise his invention”, and consequently “becomes as stupid and ignorant as it is possible for a human creature to become”. To combat these risks, say Ms Rothschild and Amartya Sen, Smith advocated an extensive system of public education. It was possible, thought Smith, that “almost the whole body of the people” should be educated—even in the “sublime” principles of science. 

Smith also worried about the divisive effect that economic specialisation would have on human relationships. He wanted state expenditure on “publick diversions” which, he argued, would help to unite people of “rank and fortune” with those of “low condition”. And Smith thought that any civilised society should be able to afford philosophers as well as butchers, brewers and bakers—all of whom contributed to society in different ways—even if some of them were not economically productive. People refer to this as Smith’s “social division of labour”. 

None of this is to argue that Smith was anti-market—or a Marxist, as some have occasionally suggested. But his ideas are not suited to isolated quotation, which generally leads to big distortions in what Smith really wanted to say.

Philosophy of space and time

From Wikipedia, the free encyclopedia

Philosophy of space and time is the branch of philosophy concerned with the issues surrounding the ontology, epistemology, and character of space and time. While such ideas have been central to philosophy from its inception, the philosophy of space and time was both an inspiration for and a central aspect of early analytic philosophy. The subject focuses on a number of basic issues, including whether time and space exist independently of the mind, whether they exist independently of one another, what accounts for time's apparently unidirectional flow, whether times other than the present moment exist, and questions about the nature of identity (particularly the nature of identity over time).

Ancient and medieval views

The earliest recorded Western philosophy of time was expounded by the ancient Egyptian thinker Ptahhotep (c. 2650–2600 BC) who said:

Follow your desire as long as you live, and do not perform more than is ordered, do not lessen the time of following desire, for the wasting of time is an abomination to the spirit...

— 11th maxim of Ptahhotep ^[1]

The Vedas, the earliest texts on Indian philosophy and Hindu philosophy, dating back to the late 2nd millennium BC, describe ancient Hindu cosmology, in which the universe goes through repeated cycles of creation, destruction, and rebirth, with each cycle lasting 4,320,000 years.^[2] Ancient Greek philosophers, including Parmenides and Heraclitus, wrote essays on the nature of time.^[3]
Incas regarded space and time as a single concept, named pacha (Quechua: pacha, Aymara: pacha).^[4][5][6]

Plato, in the Timaeus, identified time with the period of motion of the heavenly bodies, and space as that in which things come to be. Aristotle, in Book IV of his Physics, defined time as the number of changes with respect to before and after, and the place of an object as the innermost motionless boundary of that which surrounds it.

In Book 11 of St. Augustine's Confessions, he ruminates on the nature of time, asking, "What then is time? If no one asks me, I know: if I wish to explain it to one that asketh, I know not." He goes on to comment on the difficulty of thinking about time, pointing out the inaccuracy of common speech: "For but few things are there of which we speak properly; of most things we speak improperly, still the things intended are understood." ^[7] But Augustine presented the first philosophical argument for the reality of Creation (against Aristotle) in the context of his discussion of time, saying that knowledge of time depends on the knowledge of the movement of things, and therefore time cannot be where there are no creatures to measure its passing (Confessions Book XI ¶30; City of God Book XI ch.6).

In contrast to ancient Greek philosophers who believed that the universe had an infinite past with no beginning, medieval philosophers and theologians developed the concept of the universe having a finite past with a beginning, now known as Temporal finitism. The Christian philosopher John Philoponus presented early arguments, adopted by later Christian philosophers and theologians of the form "argument from the impossibility of the existence of an actual infinite", which states:^[8]

"An actual infinite cannot exist."

"An infinite temporal regress of events is an actual infinite."

"∴ An infinite temporal regress of events cannot exist."

In the early 11th century, the Muslim physicist Ibn al-Haytham (Alhacen or Alhazen) discussed space perception and its epistemological implications in his Book of Optics (1021), he also rejected Aristotle's definition of topos (Physics IV) by way of geometric demonstrations and defined place as a mathematical spatial extension.^[9] His experimental proof of the intro-mission model of vision led to changes in the understanding of the visual perception of space, contrary to the previous emission theory of vision supported by Euclid and Ptolemy. In "tying the visual perception of space to prior bodily experience, Alhacen unequivocally rejected the intuitiveness of spatial perception and, therefore, the autonomy of vision. Without tangible notions of distance and size for correlation, sight can tell us next to nothing about such things."^[10]

Realism and anti-realism

A traditional realist position in ontology is that time and space have existence apart from the human mind. Idealists, by contrast, deny or doubt the existence of objects independent of the mind. Some anti-realists, whose ontological position is that objects outside the mind do exist, nevertheless doubt the independent existence of time and space.

In 1781, Immanuel Kant published the Critique of Pure Reason, one of the most influential works in the history of the philosophy of space and time. He describes time as an a priori notion that, together with other a priori notions such as space, allows us to comprehend sense experience. Kant denies that either space or time are substance, entities in themselves, or learned by experience; he holds, rather, that both are elements of a systematic framework we use to structure our experience. Spatial measurements are used to quantify how far apart objects are, and temporal measurements are used to quantitatively compare the interval between (or duration of) events. Although space and time are held to be transcendentally ideal in this sense, they are also empirically real—that is, not mere illusions.

Idealist writers, such as J. M. E. McTaggart in The Unreality of Time, have argued that time is an illusion (see also The flow of time, below).

The writers discussed here are for the most part realists in this regard; for instance, Gottfried Leibniz held that his monads existed, at least independently of the mind of the observer.

Absolutism and relationalism

Leibniz and Newton

The great debate between defining notions of space and time as real objects themselves (absolute), or mere orderings upon actual objects (relational), began between physicists Isaac Newton (via his spokesman, Samuel Clarke) and Gottfried Leibniz in the papers of the Leibniz–Clarke correspondence.

Arguing against the absolutist position, Leibniz offers a number of thought experiments with the purpose of showing that there is contradiction in assuming the existence of facts such as absolute location and velocity. These arguments trade heavily on two principles central to his philosophy: the principle of sufficient reason and the identity of indiscernibles. The principle of sufficient reason holds that for every fact, there is a reason that is sufficient to explain what and why it is the way it is and not otherwise. The identity of indiscernibles states that if there is no way of telling two entities apart, then they are one and the same thing.

The example Leibniz uses involves two proposed universes situated in absolute space. The only discernible difference between them is that the latter is positioned five feet to the left of the first. The example is only possible if such a thing as absolute space exists. Such a situation, however, is not possible, according to Leibniz, for if it were, a universe's position in absolute space would have no sufficient reason, as it might very well have been anywhere else. Therefore, it contradicts the principle of sufficient reason, and there could exist two distinct universes that were in all ways indiscernible, thus contradicting the identity of indiscernibles.

Standing out in Clarke's (and Newton's) response to Leibniz's arguments is the bucket argument: Water in a bucket, hung from a rope and set to spin, will start with a flat surface. As the water begins to spin in the bucket, the surface of the water will become concave. If the bucket is stopped, the water will continue to spin, and while the spin continues, the surface will remain concave. The concave surface is apparently not the result of the interaction of the bucket and the water, since the surface is flat when the bucket first starts to spin, it becomes concave as the water starts to spin, and it remains concave as the bucket stops.

In this response, Clarke argues for the necessity of the existence of absolute space to account for phenomena like rotation and acceleration that cannot be accounted for on a purely relationalist account. Clarke argues that since the curvature of the water occurs in the rotating bucket as well as in the stationary bucket containing spinning water, it can only be explained by stating that the water is rotating in relation to the presence of some third thing—absolute space.

Leibniz describes a space that exists only as a relation between objects, and which has no existence apart from the existence of those objects. Motion exists only as a relation between those objects. Newtonian space provided the absolute frame of reference within which objects can have motion. In Newton's system, the frame of reference exists independently of the objects contained within it. These objects can be described as moving in relation to space itself. For many centuries, the evidence of a concave water surface held authority.

Mach

Another important figure in this debate is 19th-century physicist Ernst Mach. While he did not deny the existence of phenomena like that seen in the bucket argument, he still denied the absolutist conclusion by offering a different answer as to what the bucket was rotating in relation to: the fixed stars.

Mach suggested that thought experiments like the bucket argument are problematic. If we were to imagine a universe that only contains a bucket, on Newton's account, this bucket could be set to spin relative to absolute space, and the water it contained would form the characteristic concave surface. But in the absence of anything else in the universe, it would be difficult to confirm that the bucket was indeed spinning. It seems equally possible that the surface of the water in the bucket would remain flat.

Mach argued that, in effect, the water experiment in an otherwise empty universe would remain flat. But if another object were introduced into this universe, perhaps a distant star, there would now be something relative to which the bucket could be seen as rotating. The water inside the bucket could possibly have a slight curve. To account for the curve that we observe, an increase in the number of objects in the universe also increases the curvature in the water. Mach argued that the momentum of an object, whether angular or linear, exists as a result of the sum of the effects of other objects in the universe (Mach's Principle).

Einstein

Albert Einstein proposed that the laws of physics should be based on the principle of relativity. This principle holds that the rules of physics must be the same for all observers, regardless of the frame of reference that is used, and that light propagates at the same speed in all reference frames. This theory was motivated by Maxwell's equations, which show that electromagnetic waves propagate in a vacuum at the speed of light. However, Maxwell's equations give no indication of what this speed is relative to. Prior to Einstein, it was thought that this speed was relative to a fixed medium, called the luminiferous ether. In contrast, the theory of special relativity postulates that light propagates at the speed of light in all inertial frames, and examines the implications of this postulate.

All attempts to measure any speed relative to this ether failed, which can be seen as a confirmation of Einstein's postulate that light propagates at the same speed in all reference frames. Special relativity is a formalization of the principle of relativity that does not contain a privileged inertial frame of reference, such as the luminiferous ether or absolute space, from which Einstein inferred that no such frame exists.

Einstein generalized relativity to frames of reference that were non-inertial. He achieved this by positing the Equivalence Principle, which states that the force felt by an observer in a given gravitational field and that felt by an observer in an accelerating frame of reference are indistinguishable. This led to the conclusion that the mass of an object warps the geometry of the space-time surrounding it, as described in Einstein's field equations.

In classical physics, an inertial reference frame is one in which an object that experiences no forces does not accelerate. In general relativity, an inertial frame of reference is one that is following a geodesic of space-time. An object that moves against a geodesic experiences a force. An object in free fall does not experience a force, because it is following a geodesic. An object standing on the earth, however, will experience a force, as it is being held against the geodesic by the surface of the planet. In light of this, the bucket of water rotating in empty space will experience a force because it rotates with respect to the geodesic. The water will become concave, not because it is rotating with respect to the distant stars, but because it is rotating with respect to the geodesic.

Einstein partially advocates Mach's principle in that distant stars explain inertia because they provide the gravitational field against which acceleration and inertia occur. But contrary to Leibniz's account, this warped space-time is as integral a part of an object as are its other defining characteristics, such as volume and mass. If one holds, contrary to idealist beliefs, that objects exist independently of the mind, it seems that relativistics commits them to also hold that space and temporality have exactly the same type of independent existence.

Conventionalism

The position of conventionalism states that there is no fact of the matter as to the geometry of space and time, but that it is decided by convention. The first proponent of such a view, Henri Poincaré, reacting to the creation of the new non-Euclidean geometry, argued that which geometry applied to a space was decided by convention, since different geometries will describe a set of objects equally well, based on considerations from his sphere-world.

This view was developed and updated to include considerations from relativistic physics by Hans Reichenbach. Reichenbach's conventionalism, applying to space and time, focuses around the idea of coordinative definition.

Coordinative definition has two major features. The first has to do with coordinating units of length with certain physical objects. This is motivated by the fact that we can never directly apprehend length. Instead we must choose some physical object, say the Standard Metre at the Bureau International des Poids et Mesures (International Bureau of Weights and Measures), or the wavelength of cadmium to stand in as our unit of length. The second feature deals with separated objects. Although we can, presumably, directly test the equality of length of two measuring rods when they are next to one another, we can not find out as much for two rods distant from one another. Even supposing that two rods, whenever brought near to one another are seen to be equal in length, we are not justified in stating that they are always equal in length. This impossibility undermines our ability to decide the equality of length of two distant objects. Sameness of length, to the contrary, must be set by definition.

Such a use of coordinative definition is in effect, on Reichenbach's conventionalism, in the General Theory of Relativity where light is assumed, i.e. not discovered, to mark out equal distances in equal times. After this setting of coordinative definition, however, the geometry of spacetime is set.

As in the absolutism/relationalism debate, contemporary philosophy is still in disagreement as to the correctness of the conventionalist doctrine.

Structure of space-time

Building from a mix of insights from the historical debates of absolutism and conventionalism as well as reflecting on the import of the technical apparatus of the General Theory of Relativity, details as to the structure of space-time have made up a large proportion of discussion within the philosophy of space and time, as well as the philosophy of physics. The following is a short list of topics.

Relativity of simultaneity

According to special relativity each point in the universe can have a different set of events that compose its present instant. This has been used in the Rietdijk–Putnam argument to demonstrate that relativity predicts a block universe in which events are fixed in four dimensions.^{[citation needed]}

Invariance vs. covariance

Bringing to bear the lessons of the absolutism/relationalism debate with the powerful mathematical tools invented in the 19th and 20th century, Michael Friedman draws a distinction between invariance upon mathematical transformation and covariance upon transformation.

Invariance, or symmetry, applies to objects, i.e. the symmetry group of a space-time theory designates what features of objects are invariant, or absolute, and which are dynamical, or variable.

Covariance applies to formulations of theories, i.e. the covariance group designates in which range of coordinate systems the laws of physics hold.

This distinction can be illustrated by revisiting Leibniz's thought experiment, in which the universe is shifted over five feet. In this example the position of an object is seen not to be a property of that object, i.e. location is not invariant. Similarly, the covariance group for classical mechanics will be any coordinate systems that are obtained from one another by shifts in position as well as other translations allowed by a Galilean transformation.

In the classical case, the invariance, or symmetry, group and the covariance group coincide, but, interestingly enough, they part ways in relativistic physics. The symmetry group of the general theory of relativity includes all differentiable transformations, i.e., all properties of an object are dynamical, in other words there are no absolute objects. The formulations of the general theory of relativity, unlike those of classical mechanics, do not share a standard, i.e., there is no single formulation paired with transformations. As such the covariance group of the general theory of relativity is just the covariance group of every theory.

Historical frameworks

A further application of the modern mathematical methods, in league with the idea of invariance and covariance groups, is to try to interpret historical views of space and time in modern, mathematical language.

In these translations, a theory of space and time is seen as a manifold paired with vector spaces, the more vector spaces the more facts there are about objects in that theory. The historical development of spacetime theories is generally seen to start from a position where many facts about objects are incorporated in that theory, and as history progresses, more and more structure is removed.

For example, Aristotelian space and time has both absolute position and special places, such as the center of the cosmos, and the circumference. Newtonian space and time has absolute position and is Galilean invariant, but does not have special positions.

Holes

With the general theory of relativity, the traditional debate between absolutism and relationalism has been shifted to whether spacetime is a substance, since the general theory of relativity largely rules out the existence of, e.g., absolute positions. One powerful argument against spacetime substantivalism, offered by John Earman is known as the "hole argument".

This is a technical mathematical argument but can be paraphrased as follows:

Define a function d as the identity function over all elements over the manifold M, excepting a small neighbourhood H belonging to M. Over H d comes to differ from identity by a smooth function.

With use of this function d we can construct two mathematical models, where the second is generated by applying d to proper elements of the first, such that the two models are identical prior to the time t=0, where t is a time function created by a foliation of spacetime, but differ after t=0.

These considerations show that, since substantivalism allows the construction of holes, that the universe must, on that view, be indeterministic. Which, Earman argues, is a case against substantivalism, as the case between determinism or indeterminism should be a question of physics, not of our commitment to substantivalism.

Direction of time

The problem of the direction of time arises directly from two contradictory facts. Firstly, the fundamental physical laws are time-reversal invariant; if a cinematographic film were taken of any process describable by means of the aforementioned laws and then played backwards, it would still portray a physically possible process. Secondly, our experience of time, at the macroscopic level, is not time-reversal invariant.^[11] Glasses can fall and break, but shards of glass cannot reassemble and fly up onto tables. We have memories of the past, and none of the future. We feel we can't change the past but can influence the future.

Causation solution

One solution to this problem takes a metaphysical view, in which the direction of time follows from an asymmetry of causation. We know more about the past because the elements of the past are causes for the effect that is our perception. We feel we can't affect the past and can affect the future because we can't affect the past and can affect the future.

There are two main objections to this view. First is the problem of distinguishing the cause from the effect in a non-arbitrary way. The use of causation in constructing a temporal ordering could easily become circular. The second problem with this view is its explanatory power. While the causation account, if successful, may account for some time-asymmetric phenomena like perception and action, it does not account for many others.

However, asymmetry of causation can be observed in a non-arbitrary way which is not metaphysical in the case of a human hand dropping a cup of water which smashes into fragments on a hard floor, spilling the liquid. In this order, the causes of the resultant pattern of cup fragments and water spill is easily attributable in terms of the trajectory of the cup, irregularities in its structure, angle of its impact on the floor, etc. However, applying the same event in reverse, it is difficult to explain why the various pieces of the cup should fly up into the human hand and reassemble precisely into the shape of a cup, or why the water should position itself entirely within the cup. The causes of the resultant structure and shape of the cup and the encapsulation of the water by the hand within the cup are not easily attributable, as neither hand nor floor can achieve such formations of the cup or water. This asymmetry is perceivable on account of two features: i) the relationship between the agent capacities of the human hand (i.e., what it is and is not capable of and what it is for) and non-animal agency (i.e., what floors are and are not capable of and what they are for) and ii) that the pieces of cup came to possess exactly the nature and number of those of a cup before assembling. In short, such asymmetry is attributable to the relationship between temporal direction on the one hand and the implications of form and functional capacity on the other.

The application of these ideas of form and functional capacity only dictates temporal direction in relation to complex scenarios involving specific, non-metaphysical agency which is not merely dependent on human perception of time. However, this last observation in itself is not sufficient to invalidate the implications of the example for the progressive nature of time in general.

Thermodynamics solution

The second major family of solutions to this problem, and by far the one that has generated the most literature, finds the existence of the direction of time as relating to the nature of thermodynamics.

The answer from classical thermodynamics states that while our basic physical theory is, in fact, time-reversal symmetric, thermodynamics is not. In particular, the second law of thermodynamics states that the net entropy of a closed system never decreases, and this explains why we often see glass breaking, but not coming back together.

But in statistical mechanics things become more complicated. On one hand, statistical mechanics is far superior to classical thermodynamics, in that thermodynamic behavior, such as glass breaking, can be explained by the fundamental laws of physics paired with a statistical postulate. But statistical mechanics, unlike classical thermodynamics, is time-reversal symmetric. The second law of thermodynamics, as it arises in statistical mechanics, merely states that it is overwhelmingly likely that net entropy will increase, but it is not an absolute law.

Current thermodynamic solutions to the problem of the direction of time aim to find some further fact, or feature of the laws of nature to account for this discrepancy.

Laws solution

A third type of solution to the problem of the direction of time, although much less represented, argues that the laws are not time-reversal symmetric. For example, certain processes in quantum mechanics, relating to the weak nuclear force, are not time-reversible, keeping in mind that when dealing with quantum mechanics time-reversibility comprises a more complex definition. But this type of solution is insufficient because 1) the time-asymmetric phenomena in quantum mechanics are too few to account for the uniformity of macroscopic time-asymmetry and 2) it relies on the assumption that quantum mechanics is the final or correct description of physical processes.^{[citation needed]}

One recent proponent of the laws solution is Tim Maudlin who argues that the fundamental laws of physics are laws of temporal evolution (see Maudlin [2007]). However, elsewhere Maudlin argues: "[the] passage of time is an intrinsic asymmetry in the temporal structure of the world... It is the asymmetry that grounds the distinction between sequences that runs from past to future and sequences which run from future to past" [ibid, 2010 edition, p. 108]. Thus it is arguably difficult to assess whether Maudlin is suggesting that the direction of time is a consequence of the laws or is itself primitive.

Flow of time

The problem of the flow of time, as it has been treated in analytic philosophy, owes its beginning to a paper written by J. M. E. McTaggart. In this paper McTaggart proposes two "temporal series". The first series, which means to account for our intuitions about temporal becoming, or the moving Now, is called the A-series. The A-series orders events according to their being in the past, present or future, simpliciter and in comparison to each other. The B-series eliminates all reference to the present, and the associated temporal modalities of past and future, and orders all events by the temporal relations earlier than and later than.

McTaggart, in his paper "The Unreality of Time", argues that time is unreal since a) the A-series is inconsistent and b) the B-series alone cannot account for the nature of time as the A-series describes an essential feature of it.

Building from this framework, two camps of solution have been offered. The first, the A-theorist solution, takes becoming as the central feature of time, and tries to construct the B-series from the A-series by offering an account of how B-facts come to be out of A-facts. The second camp, the B-theorist solution, takes as decisive McTaggart's arguments against the A-series and tries to construct the A-series out of the B-series, for example, by temporal indexicals.

Dualities

Quantum field theory models have shown that it is possible for theories in two different space-time backgrounds, like AdS/CFT or T-duality, to be equivalent.

Presentism and eternalism

According to Presentism, time is an ordering of various realities. At a certain time some things exist and others do not. This is the only reality we can deal with and we cannot for example say that Homer exists because at the present time he does not. An Eternalist, on the other hand, holds that time is a dimension of reality on a par with the three spatial dimensions, and hence that all things—past, present, and future—can be said to be just as real as things in the present. According to this theory, then, Homer really does exist, though we must still use special language when talking about somebody who exists at a distant time—just as we would use special language when talking about something far away (the very words near, far, above, below, and such are directly comparable to phrases such as in the past, a minute ago, and so on).

Endurantism and perdurantism

The positions on the persistence of objects are somewhat similar. An endurantist holds that for an object to persist through time is for it to exist completely at different times (each instance of existence we can regard as somehow separate from previous and future instances, though still numerically identical with them). A perdurantist on the other hand holds that for a thing to exist through time is for it to exist as a continuous reality, and that when we consider the thing as a whole we must consider an aggregate of all its "temporal parts" or instances of existing. Endurantism is seen as the conventional view and flows out of our pre-philosophical ideas (when I talk to somebody I think I am talking to that person as a complete object, and not just a part of a cross-temporal being), but perdurantists have attacked this position. (An example of a perdurantist is David Lewis.) One argument perdurantists use to state the superiority of their view is that perdurantism is able to take account of change in objects.
The relations between these two questions mean that on the whole Presentists are also endurantists and Eternalists are also perdurantists (and vice versa), but this is not a necessary connection and it is possible to claim, for instance, that time's passage indicates a series of ordered realities, but that objects within these realities somehow exist outside of the reality as a whole, even though the realities as wholes are not related. However, such positions are rarely adopted.

Introduction to general relativity

From Wikipedia, the free encyclopedia

High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation that was developed by Albert Einstein between 1907 and 1915. According to general relativity, the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion.

Experiments and observations show that Einstein's description of gravitation accounts for several effects that are unexplained by Newton's law, such as minute anomalies in the orbits of Mercury and other planets. General relativity also predicts novel effects of gravity, such as gravitational waves, gravitational lensing and an effect of gravity on time known as gravitational time dilation. Many of these predictions have been confirmed by experiment or observation, most recently gravitational waves.

General relativity has developed into an essential tool in modern astrophysics. It provides the foundation for the current understanding of black holes, regions of space where the gravitational effect is strong enough that even light cannot escape. Their strong gravity is thought to be responsible for the intense radiation emitted by certain types of astronomical objects (such as active galactic nuclei or microquasars). General relativity is also part of the framework of the standard Big Bang model of cosmology.

Although general relativity is not the only relativistic theory of gravity, it is the simplest such theory that is consistent with the experimental data. Nevertheless, a number of open questions remain, the most fundamental of which is how general relativity can be reconciled with the laws of quantum physics to produce a complete and self-consistent theory of quantum gravity.

From special to general relativity

In September 1905, Albert Einstein published his theory of special relativity, which reconciles Newton's laws of motion with electrodynamics (the interaction between objects with electric charge). Special relativity introduced a new framework for all of physics by proposing new concepts of space and time. Some then-accepted physical theories were inconsistent with that framework; a key example was Newton's theory of gravity, which describes the mutual attraction experienced by bodies due to their mass.

Several physicists, including Einstein, searched for a theory that would reconcile Newton's law of gravity and special relativity. Only Einstein's theory proved to be consistent with experiments and observations. To understand the theory's basic ideas, it is instructive to follow Einstein's thinking between 1907 and 1915, from his simple thought experiment involving an observer in free fall to his fully geometric theory of gravity.^[1]

Equivalence principle

A person in a free-falling elevator experiences weightlessness; objects either float motionless or drift at constant speed. Since everything in the elevator is falling together, no gravitational effect can be observed. In this way, the experiences of an observer in free fall are indistinguishable from those of an observer in deep space, far from any significant source of gravity. Such observers are the privileged ("inertial") observers Einstein described in his theory of special relativity: observers for whom light travels along straight lines at constant speed.^[2]
Einstein hypothesized that the similar experiences of weightless observers and inertial observers in special relativity represented a fundamental property of gravity, and he made this the cornerstone of his theory of general relativity, formalized in his equivalence principle. Roughly speaking, the principle states that a person in a free-falling elevator cannot tell that they are in free fall. Every experiment in such a free-falling environment has the same results as it would for an observer at rest or moving uniformly in deep space, far from all sources of gravity.^[3]

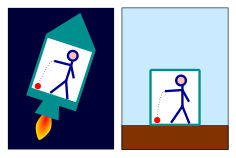
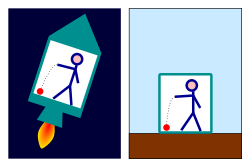
Gravity and acceleration

Ball falling to the floor in an accelerating rocket (left) and on Earth (right). The effect is identical.

Most effects of gravity vanish in free fall, but effects that seem the same as those of gravity can be produced by an accelerated frame of reference. An observer in a closed room cannot tell which of the following is true:

• Objects are falling to the floor because the room is resting on the surface of the Earth and the objects are being pulled down by gravity.
• Objects are falling to the floor because the room is aboard a rocket in space, which is accelerating at 9.81 m/s² and is far from any source of gravity. The objects are being pulled towards the floor by the same "inertial force" that presses the driver of an accelerating car into the back of his seat.

Conversely, any effect observed in an accelerated reference frame should also be observed in a gravitational field of corresponding strength. This principle allowed Einstein to predict several novel effects of gravity in 1907, as explained in the next section.

An observer in an accelerated reference frame must introduce what physicists call fictitious forces to account for the acceleration experienced by himself and objects around him. One example, the force pressing the driver of an accelerating car into his or her seat, has already been mentioned; another is the force you can feel pulling your arms up and out if you attempt to spin around like a top. Einstein's master insight was that the constant, familiar pull of the Earth's gravitational field is fundamentally the same as these fictitious forces.^[4] The apparent magnitude of the fictitious forces always appears to be proportional to the mass of any object on which they act – for instance, the driver's seat exerts just enough force to accelerate the driver at the same rate as the car. By analogy, Einstein proposed that an object in a gravitational field should feel a gravitational force proportional to its mass, as embodied in Newton's law of gravitation.^[5]

Physical consequences

In 1907, Einstein was still eight years away from completing the general theory of relativity. Nonetheless, he was able to make a number of novel, testable predictions that were based on his starting point for developing his new theory: the equivalence principle.^[6]

The gravitational redshift of a light wave as it moves upwards against a gravitational field (caused by the yellow star below).

The first new effect is the gravitational frequency shift of light. Consider two observers aboard an accelerating rocket-ship. Aboard such a ship, there is a natural concept of "up" and "down": the direction in which the ship accelerates is "up", and unattached objects accelerate in the opposite direction, falling "downward". Assume that one of the observers is "higher up" than the other. When the lower observer sends a light signal to the higher observer, the acceleration causes the light to be red-shifted, as may be calculated from special relativity; the second observer will measure a lower frequency for the light than the first. Conversely, light sent from the higher observer to the lower is blue-shifted, that is, shifted towards higher frequencies.^[7] Einstein argued that such frequency shifts must also be observed in a gravitational field. This is illustrated in the figure at left, which shows a light wave that is gradually red-shifted as it works its way upwards against the gravitational acceleration. This effect has been confirmed experimentally, as described below.

This gravitational frequency shift corresponds to a gravitational time dilation: Since the "higher" observer measures the same light wave to have a lower frequency than the "lower" observer, time must be passing faster for the higher observer. Thus, time runs more slowly for observers who are lower in a gravitational field.

It is important to stress that, for each observer, there are no observable changes of the flow of time for events or processes that are at rest in his or her reference frame. Five-minute-eggs as timed by each observer's clock have the same consistency; as one year passes on each clock, each observer ages by that amount; each clock, in short, is in perfect agreement with all processes happening in its immediate vicinity. It is only when the clocks are compared between separate observers that one can notice that time runs more slowly for the lower observer than for the higher.^[8] This effect is minute, but it too has been confirmed experimentally in multiple experiments, as described below.

In a similar way, Einstein predicted the gravitational deflection of light: in a gravitational field, light is deflected downward. Quantitatively, his results were off by a factor of two; the correct derivation requires a more complete formulation of the theory of general relativity, not just the equivalence principle.^[9]

Tidal effects

Two bodies falling towards the center of the Earth accelerate towards each other as they fall.

The equivalence between gravitational and inertial effects does not constitute a complete theory of gravity. When it comes to explaining gravity near our own location on the Earth's surface, noting that our reference frame is not in free fall, so that fictitious forces are to be expected, provides a suitable explanation. But a freely falling reference frame on one side of the Earth cannot explain why the people on the opposite side of the Earth experience a gravitational pull in the opposite direction.

A more basic manifestation of the same effect involves two bodies that are falling side by side towards the Earth. In a reference frame that is in free fall alongside these bodies, they appear to hover weightlessly – but not exactly so. These bodies are not falling in precisely the same direction, but towards a single point in space: namely, the Earth's center of gravity. Consequently, there is a component of each body's motion towards the other (see the figure). In a small environment such as a freely falling lift, this relative acceleration is minuscule, while for skydivers on opposite sides of the Earth, the effect is large. Such differences in force are also responsible for the tides in the Earth's oceans, so the term "tidal effect" is used for this phenomenon.

The equivalence between inertia and gravity cannot explain tidal effects – it cannot explain variations in the gravitational field.^[10] For that, a theory is needed which describes the way that matter (such as the large mass of the Earth) affects the inertial environment around it.

From acceleration to geometry

In exploring the equivalence of gravity and acceleration as well as the role of tidal forces, Einstein discovered several analogies with the geometry of surfaces. An example is the transition from an inertial reference frame (in which free particles coast along straight paths at constant speeds) to a rotating reference frame (in which extra terms corresponding to fictitious forces have to be introduced in order to explain particle motion): this is analogous to the transition from a Cartesian coordinate system (in which the coordinate lines are straight lines) to a curved coordinate system (where coordinate lines need not be straight).

A deeper analogy relates tidal forces with a property of surfaces called curvature. For gravitational fields, the absence or presence of tidal forces determines whether or not the influence of gravity can be eliminated by choosing a freely falling reference frame. Similarly, the absence or presence of curvature determines whether or not a surface is equivalent to a plane. In the summer of 1912, inspired by these analogies, Einstein searched for a geometric formulation of gravity.^[11]

The elementary objects of geometry – points, lines, triangles – are traditionally defined in three-dimensional space or on two-dimensional surfaces. In 1907, Hermann Minkowski, Einstein's former mathematics professor at the Swiss Federal Polytechnic, introduced a geometric formulation of Einstein's special theory of relativity where the geometry included not only space but also time. The basic entity of this new geometry is four-dimensional spacetime. The orbits of moving bodies are curves in spacetime; the orbits of bodies moving at constant speed without changing direction correspond to straight lines.^[12]

For surfaces, the generalization from the geometry of a plane – a flat surface – to that of a general curved surface had been described in the early 19th century by Carl Friedrich Gauss. This description had in turn been generalized to higher-dimensional spaces in a mathematical formalism introduced by Bernhard Riemann in the 1850s. With the help of Riemannian geometry, Einstein formulated a geometric description of gravity in which Minkowski's spacetime is replaced by distorted, curved spacetime, just as curved surfaces are a generalization of ordinary plane surfaces. Embedding Diagrams are used to illustrate curved spacetime in educational contexts.^[13][14]

After he had realized the validity of this geometric analogy, it took Einstein a further three years to find the missing cornerstone of his theory: the equations describing how matter influences spacetime's curvature. Having formulated what are now known as Einstein's equations (or, more precisely, his field equations of gravity), he presented his new theory of gravity at several sessions of the Prussian Academy of Sciences in late 1915, culminating in his final presentation on November 25, 1915.^[15]

Geometry and gravitation

Paraphrasing John Wheeler, Einstein's geometric theory of gravity can be summarized thus:

spacetime tells matter how to move; matter tells spacetime how to curve.^[16] What this means is addressed in the following three sections, which explore the motion of so-called test particles, examine which properties of matter serve as a source for gravity, and, finally, introduce Einstein's equations, which relate these matter properties to the curvature of spacetime.

Probing the gravitational field

Converging geodesics: two lines of longitude (green) that start out in parallel at the equator (red) but converge to meet at the pole.

In order to map a body's gravitational influence, it is useful to think about what physicists call probe or test particles: particles that are influenced by gravity, but are so small and light that we can neglect their own gravitational effect. In the absence of gravity and other external forces, a test particle moves along a straight line at a constant speed. In the language of spacetime, this is equivalent to saying that such test particles move along straight world lines in spacetime. In the presence of gravity, spacetime is non-Euclidean, or curved, and in curved spacetime straight world lines may not exist. Instead, test particles move along lines called geodesics, which are "as straight as possible", that is, they follow the shortest path between starting and ending points, taking the curvature into consideration.

A simple analogy is the following: In geodesy, the science of measuring Earth's size and shape, a geodesic (from Greek "geo", Earth, and "daiein", to divide) is the shortest route between two points on the Earth's surface. Approximately, such a route is a segment of a great circle, such as a line of longitude or the equator. These paths are certainly not straight, simply because they must follow the curvature of the Earth's surface. But they are as straight as is possible subject to this constraint.

The properties of geodesics differ from those of straight lines. For example, on a plane, parallel lines never meet, but this is not so for geodesics on the surface of the Earth: for example, lines of longitude are parallel at the equator, but intersect at the poles. Analogously, the world lines of test particles in free fall are spacetime geodesics, the straightest possible lines in spacetime. But still there are crucial differences between them and the truly straight lines that can be traced out in the gravity-free spacetime of special relativity. In special relativity, parallel geodesics remain parallel. In a gravitational field with tidal effects, this will not, in general, be the case. If, for example, two bodies are initially at rest relative to each other, but are then dropped in the Earth's gravitational field, they will move towards each other as they fall towards the Earth's center.^[17]

Compared with planets and other astronomical bodies, the objects of everyday life (people, cars, houses, even mountains) have little mass. Where such objects are concerned, the laws governing the behavior of test particles are sufficient to describe what happens. Notably, in order to deflect a test particle from its geodesic path, an external force must be applied. A chair someone is sitting on applies an external upwards force preventing the person from falling freely towards the center of the Earth and thus following a geodesic, which they would otherwise be doing without matter in between them and the center of the Earth. In this way, general relativity explains the daily experience of gravity on the surface of the Earth not as the downwards pull of a gravitational force, but as the upwards push of external forces. These forces deflect all bodies resting on the Earth's surface from the geodesics they would otherwise follow.^[18] For matter objects whose own gravitational influence cannot be neglected, the laws of motion are somewhat more complicated than for test particles, although it remains true that spacetime tells matter how to move.^[19]

Sources of gravity

In Newton's description of gravity, the gravitational force is caused by matter. More precisely, it is caused by a specific property of material objects: their mass. In Einstein's theory and related theories of gravitation, curvature at every point in spacetime is also caused by whatever matter is present. Here, too, mass is a key property in determining the gravitational influence of matter. But in a relativistic theory of gravity, mass cannot be the only source of gravity. Relativity links mass with energy, and energy with momentum.

The equivalence between mass and energy, as expressed by the formula E = mc², is the most famous consequence of special relativity. In relativity, mass and energy are two different ways of describing one physical quantity. If a physical system has energy, it also has the corresponding mass, and vice versa. In particular, all properties of a body that are associated with energy, such as its temperature or the binding energy of systems such as nuclei or molecules, contribute to that body's mass, and hence act as sources of gravity.^[20]

In special relativity, energy is closely connected to momentum. Just as space and time are, in that theory, different aspects of a more comprehensive entity called spacetime, energy and momentum are merely different aspects of a unified, four-dimensional quantity that physicists call four-momentum. In consequence, if energy is a source of gravity, momentum must be a source as well. The same is true for quantities that are directly related to energy and momentum, namely internal pressure and tension. Taken together, in general relativity it is mass, energy, momentum, pressure and tension that serve as sources of gravity: they are how matter tells spacetime how to curve. In the theory's mathematical formulation, all these quantities are but aspects of a more general physical quantity called the energy–momentum tensor.^[21]

Einstein's equations

Einstein's equations are the centerpiece of general relativity. They provide a precise formulation of the relationship between spacetime geometry and the properties of matter, using the language of mathematics. More concretely, they are formulated using the concepts of Riemannian geometry, in which the geometric properties of a space (or a spacetime) are described by a quantity called a metric. The metric encodes the information needed to compute the fundamental geometric notions of distance and angle in a curved space (or spacetime).

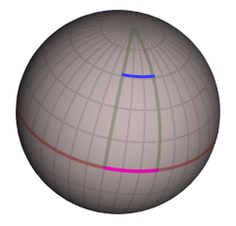
Distances, at different latitudes, corresponding to 30 degrees difference in longitude.

A spherical surface like that of the Earth provides a simple example. The location of any point on the surface can be described by two coordinates: the geographic latitude and longitude. Unlike the Cartesian coordinates of the plane, coordinate differences are not the same as distances on the surface, as shown in the diagram on the right: for someone at the equator, moving 30 degrees of longitude westward (magenta line) corresponds to a distance of roughly 3,300 kilometers (2,100 mi). On the other hand, someone at a latitude of 55 degrees, moving 30 degrees of longitude westward (blue line) covers a distance of merely 1,900 kilometers (1,200 mi). Coordinates therefore do not provide enough information to describe the geometry of a spherical surface, or indeed the geometry of any more complicated space or spacetime. That information is precisely what is encoded in the metric, which is a function defined at each point of the surface (or space, or spacetime) and relates coordinate differences to differences in distance. All other quantities that are of interest in geometry, such as the length of any given curve, or the angle at which two curves meet, can be computed from this metric function.^[22]

The metric function and its rate of change from point to point can be used to define a geometrical quantity called the Riemann curvature tensor, which describes exactly how the space or spacetime is curved at each point. In general relativity, the metric and the Riemann curvature tensor are quantities defined at each point in spacetime. As has already been mentioned, the matter content of the spacetime defines another quantity, the energy–momentum tensor T, and the principle that "spacetime tells matter how to move, and matter tells spacetime how to curve" means that these quantities must be related to each other. Einstein formulated this relation by using the Riemann curvature tensor and the metric to define another geometrical quantity G, now called the Einstein tensor, which describes some aspects of the way spacetime is curved. Einstein's equation then states that

${\displaystyle \mathbf {G} ={\frac {8\pi G}{c^{4}}}\mathbf {T} ,}$

i.e., up to a constant multiple, the quantity G (which measures curvature) is equated with the quantity T (which measures matter content). Here, G is the gravitational constant of Newtonian gravity, and c is the speed of light from special relativity.

This equation is often referred to in the plural as Einstein's equations, since the quantities G and T are each determined by several functions of the coordinates of spacetime, and the equations equate each of these component functions.^[23] A solution of these equations describes a particular geometry of spacetime; for example, the Schwarzschild solution describes the geometry around a spherical, non-rotating mass such as a star or a black hole, whereas the Kerr solution describes a rotating black hole. Still other solutions can describe a gravitational wave or, in the case of the Friedmann–Lemaître–Robertson–Walker solution, an expanding universe. The simplest solution is the uncurved Minkowski spacetime, the spacetime described by special relativity.^[24]

Experiments

No scientific theory is apodictically true; each is a model that must be checked by experiment. Newton's law of gravity was accepted because it accounted for the motion of planets and moons in the Solar System with considerable accuracy. As the precision of experimental measurements gradually improved, some discrepancies with Newton's predictions were observed, and these were accounted for in the general theory of relativity. Similarly, the predictions of general relativity must also be checked with experiment, and Einstein himself devised three tests now known as the classical tests of the theory:

Newtonian (red) vs. Einsteinian orbit (blue) of a single planet orbiting a spherical star. (Click on the image for animation.)

• Newtonian gravity predicts that the orbit which a single planet traces around a perfectly spherical star should be an ellipse. Einstein's theory predicts a more complicated curve: the planet behaves as if it were travelling around an ellipse, but at the same time, the ellipse as a whole is rotating slowly around the star. In the diagram on the right, the ellipse predicted by Newtonian gravity is shown in red, and part of the orbit predicted by Einstein in blue. For a planet orbiting the Sun, this deviation from Newton's orbits is known as the anomalous perihelion shift. The first measurement of this effect, for the planet Mercury, dates back to 1859. The most accurate results for Mercury and for other planets to date are based on measurements which were undertaken between 1966 and 1990, using radio telescopes.^[25] General relativity predicts the correct anomalous perihelion shift for all planets where this can be measured accurately (Mercury, Venus and the Earth).
• According to general relativity, light does not travel along straight lines when it propagates in a gravitational field. Instead, it is deflected in the presence of massive bodies. In particular, starlight is deflected as it passes near the Sun, leading to apparent shifts of up 1.75 arc seconds in the stars' positions in the sky (an arc second is equal to 1/3600 of a degree). In the framework of Newtonian gravity, a heuristic argument can be made that leads to light deflection by half that amount. The different predictions can be tested by observing stars that are close to the Sun during a solar eclipse. In this way, a British expedition to West Africa in 1919, directed by Arthur Eddington, confirmed that Einstein's prediction was correct, and the Newtonian predictions wrong, via observation of the May 1919 eclipse. Eddington's results were not very accurate; subsequent observations of the deflection of the light of distant quasars by the Sun, which utilize highly accurate techniques of radio astronomy, have confirmed Eddington's results with significantly better precision (the first such measurements date from 1967, the most recent comprehensive analysis from 2004).^[26]
• Gravitational redshift was first measured in a laboratory setting in 1959 by Pound and Rebka. It is also seen in astrophysical measurements, notably for light escaping the white dwarf Sirius B. The related gravitational time dilation effect has been measured by transporting atomic clocks to altitudes of between tens and tens of thousands of kilometers (first by Hafele and Keating in 1971; most accurately to date by Gravity Probe A launched in 1976).^[27]

Of these tests, only the perihelion advance of Mercury was known prior to Einstein's final publication of general relativity in 1916. The subsequent experimental confirmation of his other predictions, especially the first measurements of the deflection of light by the sun in 1919, catapulted Einstein to international stardom.^[28] These three experiments justified adopting general relativity over Newton's theory and, incidentally, over a number of alternatives to general relativity that had been proposed.

Gravity Probe B with solar panels folded.

Further tests of general relativity include precision measurements of the Shapiro effect or gravitational time delay for light, most recently in 2002 by the Cassini space probe. One set of tests focuses on effects predicted by general relativity for the behavior of gyroscopes travelling through space. One of these effects, geodetic precession, has been tested with the Lunar Laser Ranging Experiment (high-precision measurements of the orbit of the Moon). Another, which is related to rotating masses, is called frame-dragging. The geodetic and frame-dragging effects were both tested by the Gravity Probe B satellite experiment launched in 2004, with results confirming relativity to within 0.5% and 15%, respectively, as of December 2008.^[29]

By cosmic standards, gravity throughout the solar system is weak. Since the differences between the predictions of Einstein's and Newton's theories are most pronounced when gravity is strong, physicists have long been interested in testing various relativistic effects in a setting with comparatively strong gravitational fields. This has become possible thanks to precision observations of binary pulsars. In such a star system, two highly compact neutron stars orbit each other. At least one of them is a pulsar – an astronomical object that emits a tight beam of radiowaves. These beams strike the Earth at very regular intervals, similarly to the way that the rotating beam of a lighthouse means that an observer sees the lighthouse blink, and can be observed as a highly regular series of pulses. General relativity predicts specific deviations from the regularity of these radio pulses. For instance, at times when the radio waves pass close to the other neutron star, they should be deflected by the star's gravitational field. The observed pulse patterns are impressively close to those predicted by general relativity.^[30]

One particular set of observations is related to eminently useful practical applications, namely to satellite navigation systems such as the Global Positioning System that are used both for precise positioning and timekeeping. Such systems rely on two sets of atomic clocks: clocks aboard satellites orbiting the Earth, and reference clocks stationed on the Earth's surface. General relativity predicts that these two sets of clocks should tick at slightly different rates, due to their different motions (an effect already predicted by special relativity) and their different positions within the Earth's gravitational field. In order to ensure the system's accuracy, the satellite clocks are either slowed down by a relativistic factor, or that same factor is made part of the evaluation algorithm. In turn, tests of the system's accuracy (especially the very thorough measurements that are part of the definition of universal coordinated time) are testament to the validity of the relativistic predictions.^[31]

A number of other tests have probed the validity of various versions of the equivalence principle; strictly speaking, all measurements of gravitational time dilation are tests of the weak version of that principle, not of general relativity itself. So far, general relativity has passed all observational tests.^[32]

Astrophysical applications

Models based on general relativity play an important role in astrophysics; the success of these models is further testament to the theory's validity.

Gravitational lensing

Einstein cross: four images of the same astronomical object, produced by a gravitational lens.

Since light is deflected in a gravitational field, it is possible for the light of a distant object to reach an observer along two or more paths. For instance, light of a very distant object such as a quasar can pass along one side of a massive galaxy and be deflected slightly so as to reach an observer on Earth, while light passing along the opposite side of that same galaxy is deflected as well, reaching the same observer from a slightly different direction. As a result, that particular observer will see one astronomical object in two different places in the night sky. This kind of focussing is well-known when it comes to optical lenses, and hence the corresponding gravitational effect is called gravitational lensing.^[33]

Observational astronomy uses lensing effects as an important tool to infer properties of the lensing object. Even in cases where that object is not directly visible, the shape of a lensed image provides information about the mass distribution responsible for the light deflection. In particular, gravitational lensing provides one way to measure the distribution of dark matter, which does not give off light and can be observed only by its gravitational effects. One particularly interesting application are large-scale observations, where the lensing masses are spread out over a significant fraction of the observable universe, and can be used to obtain information about the large-scale properties and evolution of our cosmos.^[34]

Gravitational waves

Gravitational waves, a direct consequence of Einstein's theory, are distortions of geometry that propagate at the speed of light, and can be thought of as ripples in spacetime. They should not be confused with the gravity waves of fluid dynamics, which are a different concept.

In February 2016, the Advanced LIGO team announced that they had directly observed gravitational waves from a black hole merger.^[35]

Indirectly, the effect of gravitational waves had been detected in observations of specific binary stars. Such pairs of stars orbit each other and, as they do so, gradually lose energy by emitting gravitational waves. For ordinary stars like the Sun, this energy loss would be too small to be detectable, but this energy loss was observed in 1974 in a binary pulsar called PSR1913+16. In such a system, one of the orbiting stars is a pulsar. This has two consequences: a pulsar is an extremely dense object known as a neutron star, for which gravitational wave emission is much stronger than for ordinary stars. Also, a pulsar emits a narrow beam of electromagnetic radiation from its magnetic poles. As the pulsar rotates, its beam sweeps over the Earth, where it is seen as a regular series of radio pulses, just as a ship at sea observes regular flashes of light from the rotating light in a lighthouse. This regular pattern of radio pulses functions as a highly accurate "clock". It can be used to time the double star's orbital period, and it reacts sensitively to distortions of spacetime in its immediate neighborhood.

The discoverers of PSR1913+16, Russell Hulse and Joseph Taylor, were awarded the Nobel Prize in Physics in 1993. Since then, several other binary pulsars have been found. The most useful are those in which both stars are pulsars, since they provide accurate tests of general relativity.^[36]

Currently, a number of land-based gravitational wave detectors are in operation, and a mission to launch a space-based detector, LISA, is currently under development, with a precursor mission (LISA Pathfinder) which was launched in 2015. Gravitational wave observations can be used to obtain information about compact objects such as neutron stars and black holes, and also to probe the state of the early universe fractions of a second after the Big Bang.^[37]

Black holes

Black hole-powered jet emanating from the central region of the galaxy M87.

When mass is concentrated into a sufficiently compact region of space, general relativity predicts the formation of a black hole – a region of space with a gravitational effect so strong that not even light can escape. Certain types of black holes are thought to be the final state in the evolution of massive stars. On the other hand, supermassive black holes with the mass of millions or billions of Suns are assumed to reside in the cores of most galaxies, and they play a key role in current models of how galaxies have formed over the past billions of years.^[38]

Matter falling onto a compact object is one of the most efficient mechanisms for releasing energy in the form of radiation, and matter falling onto black holes is thought to be responsible for some of the brightest astronomical phenomena imaginable. Notable examples of great interest to astronomers are quasars and other types of active galactic nuclei. Under the right conditions, falling matter accumulating around a black hole can lead to the formation of jets, in which focused beams of matter are flung away into space at speeds near that of light.^[39]

There are several properties that make black holes most promising sources of gravitational waves. One reason is that black holes are the most compact objects that can orbit each other as part of a binary system; as a result, the gravitational waves emitted by such a system are especially strong. Another reason follows from what are called black-hole uniqueness theorems: over time, black holes retain only a minimal set of distinguishing features (these theorems have become known as "no-hair" theorems, since different hairstyles are a crucial part of what gives different people their different appearances). For instance, in the long term, the collapse of a hypothetical matter cube will not result in a cube-shaped black hole. Instead, the resulting black hole will be indistinguishable from a black hole formed by the collapse of a spherical mass, but with one important difference: in its transition to a spherical shape, the black hole formed by the collapse of a cube will emit gravitational waves.^[40]

Cosmology

An image, created using data from the WMAP satellite telescope, of the radiation emitted no more than a few hundred thousand years after the Big Bang.

One of the most important aspects of general relativity is that it can be applied to the universe as a whole. A key point is that, on large scales, our universe appears to be constructed along very simple lines: all current observations suggest that, on average, the structure of the cosmos should be approximately the same, regardless of an observer's location or direction of observation: the universe is approximately homogeneous and isotropic. Such comparatively simple universes can be described by simple solutions of Einstein's equations. The current cosmological models of the universe are obtained by combining these simple solutions to general relativity with theories describing the properties of the universe's matter content, namely thermodynamics, nuclear- and particle physics. According to these models, our present universe emerged from an extremely dense high-temperature state – the Big Bang – roughly 14 billion years ago and has been expanding ever since.^[41]

Einstein's equations can be generalized by adding a term called the cosmological constant. When this term is present, empty space itself acts as a source of attractive (or, less commonly, repulsive) gravity. Einstein originally introduced this term in his pioneering 1917 paper on cosmology, with a very specific motivation: contemporary cosmological thought held the universe to be static, and the additional term was required for constructing static model universes within the framework of general relativity. When it became apparent that the universe is not static, but expanding, Einstein was quick to discard this additional term. Since the end of the 1990s, however, astronomical evidence indicating an accelerating expansion consistent with a cosmological constant – or, equivalently, with a particular and ubiquitous kind of dark energy – has steadily been accumulating.^[42]

Modern research

General relativity is very successful in providing a framework for accurate models which describe an impressive array of physical phenomena. On the other hand, there are many interesting open questions, and in particular, the theory as a whole is almost certainly incomplete.^[43]

In contrast to all other modern theories of fundamental interactions, general relativity is a classical theory: it does not include the effects of quantum physics. The quest for a quantum version of general relativity addresses one of the most fundamental open questions in physics. While there are promising candidates for such a theory of quantum gravity, notably string theory and loop quantum gravity, there is at present no consistent and complete theory. It has long been hoped that a theory of quantum gravity would also eliminate another problematic feature of general relativity: the presence of spacetime singularities. These singularities are boundaries ("sharp edges") of spacetime at which geometry becomes ill-defined, with the consequence that general relativity itself loses its predictive power. Furthermore, there are so-called singularity theorems which predict that such singularities must exist within the universe if the laws of general relativity were to hold without any quantum modifications. The best-known examples are the singularities associated with the model universes that describe black holes and the beginning of the universe.^[44]

Other attempts to modify general relativity have been made in the context of cosmology. In the modern cosmological models, most energy in the universe is in forms that have never been detected directly, namely dark energy and dark matter. There have been several controversial proposals to remove the need for these enigmatic forms of matter and energy, by modifying the laws governing gravity and the dynamics of cosmic expansion, for example modified Newtonian dynamics.^[45]

Beyond the challenges of quantum effects and cosmology, research on general relativity is rich with possibilities for further exploration: mathematical relativists explore the nature of singularities and the fundamental properties of Einstein's equations,^[46] and ever more comprehensive computer simulations of specific spacetimes (such as those describing merging black holes) are run.^[47] More than ninety years after the theory was first published, research is more active than ever.^[48]