| Thomas Kuhn | |
|---|---|
 |
|
| Born | Thomas Samuel Kuhn July 18, 1922 Cincinnati, Ohio, U.S. |
| Died | June 17, 1996 (aged 73) Cambridge, Massachusetts, U.S. |
| Alma mater | Harvard University |
| Era | 20th-century philosophy |
| Region | Western philosophy |
| School | Analytic Historical turn[1] |
|
Main interests
|
Philosophy of science |
|
Notable ideas
|
|
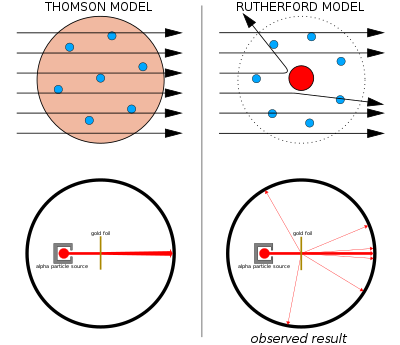
Kuhn made several notable claims concerning the progress of scientific knowledge: that scientific fields undergo periodic "paradigm shifts" rather than solely progressing in a linear and continuous way, and that these paradigm shifts open up new approaches to understanding what scientists would never have considered valid before; and that the notion of scientific truth, at any given moment, cannot be established solely by objective criteria but is defined by a consensus of a scientific community. Competing paradigms are frequently incommensurable; that is, they are competing and irreconcilable accounts of reality. Thus, our comprehension of science can never rely wholly upon "objectivity" alone. Science must account for subjective perspectives as well, since all objective conclusions are ultimately founded upon the subjective conditioning/worldview of its researchers and participants.
Life
Kuhn was born in Cincinnati, Ohio, to Samuel L. Kuhn, an industrial engineer, and Minette Stroock Kuhn, both Jewish. He graduated from The Taft School in Watertown, CT, in 1940, where he became aware of his serious interest in mathematics and physics. He obtained his BS degree in physics from Harvard University in 1943, where he also obtained MS and PhD degrees in physics in 1946 and 1949, respectively, under the supervision of John Van Vleck.[12] As he states in the first few pages of the preface to the second edition of The Structure of Scientific Revolutions, his three years of total academic freedom as a Harvard Junior Fellow were crucial in allowing him to switch from physics to the history and philosophy of science. He later taught a course in the history of science at Harvard from 1948 until 1956, at the suggestion of university president James Conant. After leaving Harvard, Kuhn taught at the University of California, Berkeley, in both the philosophy department and the history department, being named Professor of the History of science in 1961. Kuhn interviewed and tape recorded Danish physicist Niels Bohr the day before Bohr's death.[13] At Berkeley, he wrote and published (in 1962) his best known and most influential work:[14] The Structure of Scientific Revolutions. In 1964, he joined Princeton University as the M. Taylor Pyne Professor of Philosophy and History of Science. He served as the president of the History of Science Society from 1969–70.[15] In 1979 he joined the Massachusetts Institute of Technology (MIT) as the Laurance S. Rockefeller Professor of Philosophy, remaining there until 1991. In 1994 Kuhn was diagnosed with lung cancer. He died in 1996.Thomas Kuhn was married twice, first to Kathryn Muhs with whom he had three children, then to Jehane Barton Burns (Jehane R. Kuhn).
The Structure of Scientific Revolutions
The Structure of Scientific Revolutions (SSR) was originally printed as an article in the International Encyclopedia of Unified Science, published by the logical positivists of the Vienna Circle. In this book, Kuhn argued that science does not progress via a linear accumulation of new knowledge, but undergoes periodic revolutions, also called "paradigm shifts" (although he did not coin the phrase),[16] in which the nature of scientific inquiry within a particular field is abruptly transformed. In general, science is broken up into three distinct stages. Prescience, which lacks a central paradigm, comes first. This is followed by "normal science", when scientists attempt to enlarge the central paradigm by "puzzle-solving". Guided by the paradigm, normal science is extremely productive: "when the paradigm is successful, the profession will have solved problems that its members could scarcely have imagined and would never have undertaken without commitment to the paradigm".[17]In regard to experimentation and collection of data with a view toward solving problems through the commitment to a paradigm, Kuhn states: “The operations and measurements that a scientist undertakes in the laboratory are not ‘the given’ of experience but rather ‘the collected with diffculty.’ They are not what the scientist sees—at least not before his research is well advanced and his attention focused. Rather, they are concrete indices to the content of more elementary perceptions, and as such they are selected for the close scrutiny of normal research only because they promise opportunity for the fruitful elaboration of an accepted paradigm. Far more clearly than the immediate experience from which they in part derive, operations and measurements are paradigm-determined. Science does not deal in all possible laboratory manipulations. Instead, it selects those relevant to the juxtaposition of a paradigm with the immediate experience that that paradigm has partially determined. As a result, scientists with different paradigms engage in different concrete laboratory manipulations.”[18]
During the period of normal science, the failure of a result to conform to the paradigm is seen not as refuting the paradigm, but as the mistake of the researcher, contra Popper's falsifiability criterion. As anomalous results build up, science reaches a crisis, at which point a new paradigm, which subsumes the old results along with the anomalous results into one framework, is accepted. This is termed revolutionary science.
In SSR, Kuhn also argues that rival paradigms are incommensurable—that is, it is not possible to understand one paradigm through the conceptual framework and terminology of another rival paradigm. For many critics, for example David Stove (Popper and After, 1982), this thesis seemed to entail that theory choice is fundamentally irrational: if rival theories cannot be directly compared, then one cannot make a rational choice as to which one is better. Whether Kuhn's views had such relativistic consequences is the subject of much debate; Kuhn himself denied the accusation of relativism in the third edition of SSR, and sought to clarify his views to avoid further misinterpretation. Freeman Dyson has quoted Kuhn as saying "I am not a Kuhnian!",[19] referring to the relativism that some philosophers have developed based on his work.
The enormous impact of Kuhn's work can be measured in the changes it brought about in the vocabulary of the philosophy of science: besides "paradigm shift", Kuhn popularized the word "paradigm" itself from a term used in certain forms of linguistics and the work of Georg Lichtenberg to its current broader meaning, coined the term "normal science" to refer to the relatively routine, day-to-day work of scientists working within a paradigm, and was largely responsible for the use of the term "scientific revolutions" in the plural, taking place at widely different periods of time and in different disciplines, as opposed to a single scientific revolution in the late Renaissance. The frequent use of the phrase "paradigm shift" has made scientists more aware of and in many cases more receptive to paradigm changes, so that Kuhn's analysis of the evolution of scientific views has by itself influenced that evolution.[citation needed]
Kuhn's work has been extensively used in social science; for instance, in the post-positivist/positivist debate within International Relations. Kuhn is credited as a foundational force behind the post-Mertonian sociology of scientific knowledge. Kuhn's work has also been used in the Arts and Humanities, such as by Matthew Edward Harris to distinguish between scientific and historical communities (such as political or religious groups): 'political-religious beliefs and opinions are not epistemologically the same as those pertaining to scientific theories'.[20] This is because would-be scientists' worldviews are changed through rigorous training, through the engagement between what Kuhn calls 'exemplars' and the Global Paradigm. Kuhn's notions of paradigms and paradigm shifts have been influential in understanding the history of economic thought, for example the Keynesian revolution,[21] and in debates in political science.[22]
A defense Kuhn gives against the objection that his account of science from The Structure of Scientific Revolutions results in relativism can be found in an essay by Kuhn called "Objectivity, Value Judgment, and Theory Choice."[23] In this essay, he reiterates five criteria from the penultimate chapter of SSR that determine (or help determine, more properly) theory choice:
- Accurate – empirically adequate with experimentation and observation
- Consistent – internally consistent, but also externally consistent with other theories
- Broad Scope – a theory's consequences should extend beyond that which it was initially designed to explain
- Simple – the simplest explanation, principally similar to Occam's razor
- Fruitful – a theory should disclose new phenomena or new relationships among phenomena
Polanyi–Kuhn debate
Although they used different terminologies, both Kuhn and Michael Polanyi believed that scientists' subjective experiences made science a relativized discipline. Polanyi lectured on this topic for decades before Kuhn published The Structure of Scientific Revolutions.Supporters of Polanyi charged Kuhn with plagiarism, as it was known that Kuhn attended several of Polanyi's lectures, and that the two men had debated endlessly over epistemology before either had achieved fame. The charge of plagiarism is peculiar, for Kuhn had generously acknowledged Polanyi in the first edition of The Structure of Scientific Revolutions.[5] Despite this intellectual alliance, Polanyi's work was constantly interpreted by others within the framework of Kuhn's paradigm shifts, much to Polanyi's (and Kuhn's) dismay.[24]
Thomas Kuhn Paradigm Shift Award
In honor of his legacy, the "Thomas Kuhn Paradigm Shift Award" is awarded by the American Chemical Society to speakers who present original views that are at odds with mainstream scientific understanding. The winner is selected based in the novelty of the viewpoint and its potential impact if it were to be widely accepted.[25]Honors
Kuhn was named a Guggenheim Fellow in 1954, and in 1982 was awarded the George Sarton Medal by the History of Science Society. He also received numerous honorary doctorates.Bibliography
- Kuhn, T. S. The Copernican Revolution: Planetary Astronomy in the Development of Western Thought. Cambridge: Harvard University Press, 1957. ISBN 0-674-17100-4
- Kuhn, T. S. The Function of Measurement in Modern Physical Science. Isis, 52 (1961): 161–193.
- Kuhn, T. S. The Structure of Scientific Revolutions. Chicago: University of Chicago Press, 1962. ISBN 0-226-45808-3
- Kuhn, T. S. "The Function of Dogma in Scientific Research". pp. 347–69 in A. C. Crombie (ed.). Scientific Change (Symposium on the History of Science, University of Oxford, July 9–15, 1961). New York and London: Basic Books and Heineman, 1963.
- Kuhn, T. S. The Essential Tension: Selected Studies in Scientific Tradition and Change. Chicago and London: University of Chicago Press, 1977. ISBN 0-226-45805-9
- Kuhn, T. S. Black-Body Theory and the Quantum Discontinuity, 1894-1912. Chicago: University of Chicago Press, 1987. ISBN 0-226-45800-8
- Kuhn, T. S. The Road Since Structure: Philosophical Essays, 1970-1993. Chicago: University of Chicago Press, 2000. ISBN 0-226-45798-2