Optical amplifier

From Wikipedia, the free encyclopedia

Optical amplifiers are used to create laser guide stars which provide feedback to the active optics control systems which dynamically adjust the shape of the mirrors in the largest astronomical telescopes.

An optical amplifier is a device that amplifies an optical signal directly, without the need to first convert it to an electrical signal. An optical amplifier may be thought of as a laser without an optical cavity, or one in which feedback from the cavity is suppressed. Optical amplifiers are important in optical communication and laser physics. They are used as optical repeaters in the long distance fiberoptic cables which carry much of the world's telecommunication links.

There are several different physical mechanisms that can be used to amplify a light signal, which correspond to the major types of optical amplifiers. In doped fiber amplifiers and bulk lasers, stimulated emission in the amplifier's gain medium causes amplification of incoming light. In semiconductor optical amplifiers (SOAs), electron-hole recombination occurs. In Raman amplifiers, Raman scattering of incoming light with phonons in the lattice of the gain medium produces photons coherent with the incoming photons. Parametric amplifiers use parametric amplification.

Laser amplifiers

Almost any laser active gain medium can be pumped to produce gain for light at the wavelength of a laser made with the same material as its gain medium. Such amplifiers are commonly used to produce high power laser systems. Special types such as regenerative amplifiers and chirped-pulse amplifiers are used to amplify ultrashort pulses.

Solid-state amplifiers

Solid-state amplifiers are optical amplifiers that uses a wide range of doped solid-state materials (Nd:YAG, Yb:YAG, Ti:Sa) and different geometries (disk, slab, rod) to amplify optical signals. The variety of materials allows the amplification of different wavelength while the shape of the medium can distinguish between more suitable for energy of average power scaling. Beside their use in fundamental research from gravitational wave detection to high energy physics at NIF they can also be found in many today’s ultra short pulsed lasers.

Doped fiber amplifiers

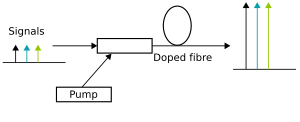
Schematic diagram of a simple Doped Fiber Amplifier

Doped fiber amplifiers (DFAs) are optical amplifiers that use a doped optical fiber as a gain medium to amplify an optical signal. They are related to fiber lasers. The signal to be amplified and a pump laser are multiplexed into the doped fiber, and the signal is amplified through interaction with the doping ions. The most common example is the Erbium Doped Fiber Amplifier (EDFA), where the core of a silica fiber is doped with trivalent erbium ions and can be efficiently pumped with a laser at a wavelength of 980 nm or 1,480 nm, and exhibits gain in the 1,550 nm region.

An erbium-doped waveguide amplifier (EDWA) is an optical amplifier that uses a waveguide to boost an optical signal.

Amplification is achieved by stimulated emission of photons from dopant ions in the doped fiber. The pump laser excites ions into a higher energy from where they can decay via stimulated emission of a photon at the signal wavelength back to a lower energy level. The excited ions can also decay spontaneously (spontaneous emission) or even through nonradiative processes involving interactions with phonons of the glass matrix. These last two decay mechanisms compete with stimulated emission reducing the efficiency of light amplification.

The amplification window of an optical amplifier is the range of optical wavelengths for which the amplifier yields a usable gain. The amplification window is determined by the spectroscopic properties of the dopant ions, the glass structure of the optical fiber, and the wavelength and power of the pump laser.

Although the electronic transitions of an isolated ion are very well defined, broadening of the energy levels occurs when the ions are incorporated into the glass of the optical fiber and thus the amplification window is also broadened. This broadening is both homogeneous (all ions exhibit the same broadened spectrum) and inhomogeneous (different ions in different glass locations exhibit different spectra). Homogeneous broadening arises from the interactions with phonons of the glass, while inhomogeneous broadening is caused by differences in the glass sites where different ions are hosted. Different sites expose ions to different local electric fields, which shifts the energy levels via the Stark effect. In addition, the Stark effect also removes the degeneracy of energy states having the same total angular momentum (specified by the quantum number J). Thus, for example, the trivalent erbium ion (Er⁺³) has a ground state with J = 15/2, and in the presence of an electric field splits into J + 1/2 = 8 sublevels with slightly different energies. The first excited state has J = 13/2 and therefore a Stark manifold with 7 sublevels. Transitions from the J = 13/2 excited state to the J= 15/2 ground state are responsible for the gain at 1.5 µm wavelength. The gain spectrum of the EDFA has several peaks that are smeared by the above broadening mechanisms. The net result is a very broad spectrum (30 nm in silica, typically). The broad gain-bandwidth of fiber amplifiers make them particularly useful in wavelength-division multiplexed communications systems as a single amplifier can be utilized to amplify all signals being carried on a fiber and whose wavelengths fall within the gain window.

Basic principle of EDFA

A relatively high-powered beam of light is mixed with the input signal using a wavelength selective coupler (WSC). The input signal and the excitation light must be at significantly different wavelengths. The mixed light is guided into a section of fiber with erbium ions included in the core. This high-powered light beam excites the erbium ions to their higher-energy state. When the photons belonging to the signal at a different wavelength from the pump light meet the excited erbium atoms, the erbium atoms give up some of their energy to the signal and return to their lower-energy state. A significant point is that the erbium gives up its energy in the form of additional photons which are exactly in the same phase and direction as the signal being amplified. So the signal is amplified along its direction of travel only. This is not unusual – when an atom “lases” it always gives up its energy in the same direction and phase as the incoming light. Thus all of the additional signal power is guided in the same fiber mode as the incoming signal. There is usually an isolator placed at the output to prevent reflections returning from the attached fiber. Such reflections disrupt amplifier operation and in the extreme case can cause the amplifier to become a laser. The erbium doped amplifier is a high gain amplifier.

Noise

The principal source of noise in DFAs is Amplified Spontaneous Emission (ASE), which has a spectrum approximately the same as the gain spectrum of the amplifier. Noise figure in an ideal DFA is 3 dB, while practical amplifiers can have noise figure as large as 6–8 dB.

As well as decaying via stimulated emission, electrons in the upper energy level can also decay by spontaneous emission, which occurs at random, depending upon the glass structure and inversion level. Photons are emitted spontaneously in all directions, but a proportion of those will be emitted in a direction that falls within the numerical aperture of the fiber and are thus captured and guided by the fiber. Those photons captured may then interact with other dopant ions, and are thus amplified by stimulated emission. The initial spontaneous emission is therefore amplified in the same manner as the signals, hence the term Amplified Spontaneous Emission. ASE is emitted by the amplifier in both the forward and reverse directions, but only the forward ASE is a direct concern to system performance since that noise will co-propagate with the signal to the receiver where it degrades system performance. Counter-propagating ASE can, however, lead to degradation of the amplifier's performance since the ASE can deplete the inversion level and thereby reduce the gain of the amplifier.

Gain saturation

Gain is achieved in a DFA due to population inversion of the dopant ions. The inversion level of a DFA is set, primarily, by the power of the pump wavelength and the power at the amplified wavelengths. As the signal power increases, or the pump power decreases, the inversion level will reduce and thereby the gain of the amplifier will be reduced. This effect is known as gain saturation – as the signal level increases, the amplifier saturates and cannot produce any more output power, and therefore the gain reduces. Saturation is also commonly known as gain compression.

To achieve optimum noise performance DFAs are operated under a significant amount of gain compression (10 dB typically), since that reduces the rate of spontaneous emission, thereby reducing ASE. Another advantage of operating the DFA in the gain saturation region is that small fluctuations in the input signal power are reduced in the output amplified signal: smaller input signal powers experience larger (less saturated) gain, while larger input powers see less gain.

The leading edge of the pulse is amplified, until the saturation energy of the gain medium is reached. In some condition, the width (FWHM) of the pulse is reduced.

Inhomogeneous broadening effects

Due to the inhomogeneous portion of the linewidth broadening of the dopant ions, the gain spectrum has an inhomogeneous component and gain saturation occurs, to a small extent, in an inhomogeneous manner. This effect is known as spectral hole burning because a high power signal at one wavelength can 'burn' a hole in the gain for wavelengths close to that signal by saturation of the inhomogeneously broadened ions. Spectral holes vary in width depending on the characteristics of the optical fiber in question and the power of the burning signal, but are typically less than 1 nm at the short wavelength end of the C-band, and a few nm at the long wavelength end of the C-band. The depth of the holes are very small, though, making it difficult to observe in practice.

Polarization effects

Although the DFA is essentially a polarization independent amplifier, a small proportion of the dopant ions interact preferentially with certain polarizations and a small dependence on the polarization of the input signal may occur (typically < 0.5 dB). This is called Polarization Dependent Gain (PDG). The absorption and emission cross sections of the ions can be modeled as ellipsoids with the major axes aligned at random in all directions in different glass sites. The random distribution of the orientation of the ellipsoids in a glass produces a macroscopically isotropic medium, but a strong pump laser induces an anisotropic distribution by selectively exciting those ions that are more aligned with the optical field vector of the pump. Also, those excited ions aligned with the signal field produce more stimulated emission. The change in gain is thus dependent on the alignment of the polarizations of the pump and signal lasers – i.e. whether the two lasers are interacting with the same sub-set of dopant ions or not. In an ideal doped fiber without birefringence, the PDG would be inconveniently large. Fortunately, in optical fibers small amounts of birefringence are always present and, furthermore, the fast and slow axes vary randomly along the fiber length. A typical DFA has several tens of meters, long enough to already show this randomness of the birefringence axes. These two combined effects (which in transmission fibers give rise to polarization mode dispersion) produce a misalignment of the relative polarizations of the signal and pump lasers along the fiber, thus tending to average out the PDG. The result is that PDG is very difficult to observe in a single amplifier (but is noticeable in links with several cascaded amplifiers).

Erbium-doped optical fiber amplifiers

The erbium-doped fiber amplifier (EDFA) is the most deployed fiber amplifier as its amplification window coincides with the third transmission window of silica-based optical fiber.

Two bands have developed in the third transmission window – the Conventional, or C-band, from approximately 1525 nm – 1565 nm, and the Long, or L-band, from approximately 1570 nm to 1610 nm. Both of these bands can be amplified by EDFAs, but it is normal to use two different amplifiers, each optimized for one of the bands.

The principal difference between C- and L-band amplifiers is that a longer length of doped fiber is used in L-band amplifiers. The longer length of fiber allows a lower inversion level to be used, thereby giving at longer wavelengths (due to the band-structure of Erbium in silica) while still providing a useful amount of gain.

EDFAs have two commonly used pumping bands – 980 nm and 1480 nm. The 980 nm band has a higher absorption cross-section and is generally used where low-noise performance is required. The absorption band is relatively narrow and so wavelength stabilised laser sources are typically needed. The 1480 nm band has a lower, but broader, absorption cross-section and is generally used for higher power amplifiers. A combination of 980 nm and 1480 nm pumping is generally utilised in amplifiers.

Gain and lasing in Erbium-doped fibers were first demonstrated in 1986–87 by two groups; one including David N. Payne, R. Mears, I.M Jauncey and L. Reekie, from the University of Southampton and one from AT&T Bell Laboratories, consisting of E. Desurvire, P. Becker, and J. Simpson. The dual-stage optical amplifier which enabled Dense Wave Division Multiplexing (DWDM,) was invented by Stephen B. Alexander at Ciena Corporation.

Doped fiber amplifiers for other wavelength ranges

Thulium doped fiber amplifiers have been used in the S-band (1450–1490 nm) and Praseodymium doped amplifiers in the 1300 nm region. However, those regions have not seen any significant commercial use so far and so those amplifiers have not been the subject of as much development as the EDFA. However, Ytterbium doped fiber lasers and amplifiers, operating near 1 micrometre wavelength, have many applications in industrial processing of materials, as these devices can be made with extremely high output power (tens of kilowatts).

Semiconductor optical amplifier

Semiconductor optical amplifiers (SOAs) are amplifiers which use a semiconductor to provide the gain medium. These amplifiers have a similar structure to Fabry–Pérot laser diodes but with anti-reflection design elements at the end faces. Recent designs include anti-reflective coatings and tilted wave guide and window regions which can reduce end face reflection to less than 0.001%. Since this creates a loss of power from the cavity which is greater than the gain, it prevents the amplifier from acting as a laser. Another type of SOA consists of two regions. One part has a structure of a Fabry-Pérot laser diode and the other has a tapered geometry in order to reduce the power density on the output facet.

Semiconductor optical amplifiers are typically made from group III-V compound semiconductors such as GaAs/AlGaAs, InP/InGaAs, InP/InGaAsP and InP/InAlGaAs, though any direct band gap semiconductors such as II-VI could conceivably be used. Such amplifiers are often used in telecommunication systems in the form of fiber-pigtailed components, operating at signal wavelengths between 0.85 µm and 1.6 µm and generating gains of up to 30 dB.

The semiconductor optical amplifier is of small size and electrically pumped. It can be potentially less expensive than the EDFA and can be integrated with semiconductor lasers, modulators, etc. However, the performance is still not comparable with the EDFA. The SOA has higher noise, lower gain, moderate polarization dependence and high nonlinearity with fast transient time. The main advantage of SOA is that all four types of nonlinear operations (cross gain modulation, cross phase modulation, wavelength conversion and four wave mixing) can be conducted. Furthermore, SOA can be run with a low power laser.^[11] This originates from the short nanosecond or less upper state lifetime, so that the gain reacts rapidly to changes of pump or signal power and the changes of gain also cause phase changes which can distort the signals. This nonlinearity presents the most severe problem for optical communication applications. However it provides the possibility for gain in different wavelength regions from the EDFA. "Linear optical amplifiers" using gain-clamping techniques have been developed.

High optical nonlinearity makes semiconductor amplifiers attractive for all optical signal processing like all-optical switching and wavelength conversion. There has been much research on semiconductor optical amplifiers as elements for optical signal processing, wavelength conversion, clock recovery, signal demultiplexing, and pattern recognition.

Vertical-cavity SOA

A recent addition to the SOA family is the vertical-cavity SOA (VCSOA). These devices are similar in structure to, and share many features with, vertical-cavity surface-emitting lasers (VCSELs). The major difference when comparing VCSOAs and VCSELs is the reduced mirror reflectivity used in the amplifier cavity. With VCSOAs, reduced feedback is necessary to prevent the device from reaching lasing threshold. Due to the extremely short cavity length, and correspondingly thin gain medium, these devices exhibit very low single-pass gain (typically on the order of a few percent) and also a very large free spectral range (FSR). The small single-pass gain requires relatively high mirror reflectivity to boost the total signal gain. In addition to boosting the total signal gain, the use of the resonant cavity structure results in a very narrow gain bandwidth; coupled with the large FSR of the optical cavity, this effectively limits operation of the VCSOA to single-channel amplification. Thus, VCSOAs can be seen as amplifying filters.

Given their vertical-cavity geometry, VCSOAs are resonant cavity optical amplifiers that operate with the input/output signal entering/exiting normal to the wafer surface. In addition to their small size, the surface normal operation of VCSOAs leads to a number of advantages, including low power consumption, low noise figure, polarization insensitive gain, and the ability to fabricate high fill factor two-dimensional arrays on a single semiconductor chip. These devices are still in the early stages of research, though promising preamplifier results have been demonstrated. Further extensions to VCSOA technology are the demonstration of wavelength tunable devices. These MEMS-tunable vertical-cavity SOAs utilize a microelectromechanical systems (MEMS) based tuning mechanism for wide and continuous tuning of the peak gain wavelength of the amplifier. SOAs have a more rapid gain response, which is in the order of 1 to 100 ps.

Tapered amplifiers

For high output power and broader wavelength range, tapered amplifiers are used. These amplifiers consist of a lateral single-mode section and a section with a tapered structure, where the laser light is amplified. The tapered structure leads to a reduction of the power density at the output facet.

Typical parameters:

• wavelength range: 633 to 1480 nm;
• input power: 10 to 50 mW;
• output power: up to 3 Watt.

Raman amplifier

In a Raman amplifier, the signal is intensified by Raman amplification. Unlike the EDFA and SOA the amplification effect is achieved by a nonlinear interaction between the signal and a pump laser within an optical fiber. There are two types of Raman amplifier: distributed and lumped. A distributed Raman amplifier is one in which the transmission fiber is utilised as the gain medium by multiplexing a pump wavelength with signal wavelength, while a lumped Raman amplifier utilises a dedicated, shorter length of fiber to provide amplification. In the case of a lumped Raman amplifier, a highly nonlinear fiber with a small core is utilised to increase the interaction between signal and pump wavelengths, and thereby reduce the length of fiber required.

The pump light may be coupled into the transmission fiber in the same direction as the signal (co-directional pumping), in the opposite direction (contra-directional pumping) or both. Contra-directional pumping is more common as the transfer of noise from the pump to the signal is reduced.

The pump power required for Raman amplification is higher than that required by the EDFA, with in excess of 500 mW being required to achieve useful levels of gain in a distributed amplifier. Lumped amplifiers, where the pump light can be safely contained to avoid safety implications of high optical powers, may use over 1 W of optical power.

The principal advantage of Raman amplification is its ability to provide distributed amplification within the transmission fiber, thereby increasing the length of spans between amplifier and regeneration sites. The amplification bandwidth of Raman amplifiers is defined by the pump wavelengths utilised and so amplification can be provided over wider, and different, regions than may be possible with other amplifier types which rely on dopants and device design to define the amplification 'window'.

Raman amplifiers have some fundamental advantages. First, Raman gain exists in every fiber, which provides a cost-effective means of upgrading from the terminal ends. Second, the gain is nonresonant, which means that gain is available over the entire transparency region of the fiber ranging from approximately 0.3 to 2µm. A third advantage of Raman amplifiers is that the gain spectrum can be tailored by adjusting the pump wavelengths. For instance, multiple pump lines can be used to increase the optical bandwidth, and the pump distribution determines the gain flatness. Another advantage of Raman amplification is that it is a relatively broad-band amplifier with a bandwidth greater than 5 THz, and the gain is reasonably flat over a wide wavelength range.

However, a number of challenges for Raman amplifiers prevented their earlier adoption. First, compared to the EDFAs, Raman amplifiers have relatively poor pumping efficiency at lower signal powers. Although a disadvantage, this lack of pump efficiency also makes gain clamping easier in Raman amplifiers. Second, Raman amplifiers require a longer gain fiber. However, this disadvantage can be mitigated by combining gain and the dispersion compensation in a single fiber. A third disadvantage of Raman amplifiers is a fast response time, which gives rise to new sources of noise, as further discussed below. Finally, there are concerns of nonlinear penalty in the amplifier for the WDM signal channels.

Optical parametric amplifier

An optical parametric amplifier allows the amplification of a weak signal-impulse in a noncentrosymmetric nonlinear medium (e.g. Beta barium borate (BBO)). In contrast to the previously mentioned amplifiers, which are mostly used in telecommunication environments, this type finds its main application in expanding the frequency tunability of ultrafast solid-state lasers (e.g. Ti:sapphire). By using a noncollinear interaction geometry optical parametric amplifiers are capable of extremely broad amplification bandwidths.

Recent achievements

The adoption of high power fiber lasers as an industrial material processing tool has been ongoing for several years and is now expanding into other markets including the medical and scientific markets. One key enhancement enabling penetration into the scientific market has been the improvements in high finesse fiber amplifiers, which are now capable of delivering single frequency linewidths (less than 5 kHz) together with excellent beam quality and stable linearly polarized output. Systems meeting these specifications, have steadily progressed in the last few years from a few Watts of output power, initially to the 10s of Watts and now into the 100s of Watts power level. This power scaling has been achieved with developments in the fiber technology, such as the adoption of stimulated brillouin scattering (SBS) suppression/mitigation techniques within the fiber, along with improvements in the overall amplifier design. The latest generation of high finesse, high power fiber amplifiers now deliver power levels exceeding what is available from commercial solid-state single frequency sources and are opening up new scientific applications as a result of the higher power levels and stable optimized performance.

Implementations

There are several simulation tools that can be used to design optical amplifiers. Popular commercial tools have been developed by Optiwave Systems and VPI Systems.

Linear optical quantum computing

From Wikipedia, the free encyclopedia

Linear Optical Quantum Computing or Linear Optics Quantum Computation (LOQC) is a paradigm of quantum computation, allowing (under certain conditions, described below) universal quantum computation. LOQC uses photons as information carriers, mainly uses linear optical elements (including beam splitters, phase shifters, and mirrors) to process quantum information, and uses photon detectors and quantum memories to detect and store quantum information.

Overview

Although there are many other implementations for quantum information processing (QIP) and quantum computation, optical quantum systems are prominent candidates, since they link quantum computation and quantum communication in the same framework. In optical systems for quantum information processing, the unit of light in a given mode—or photon—is used to represent a qubit.  Superpositions of quantum states can be easily represented, encrypted, transmitted and detected using photons. Besides, linear optical elements of optical systems may be the simplest building blocks to realize quantum operations and quantum gates. Each linear optical element equivalently applies a unitary transformation on a finite number of qubits. The system of finite linear optical elements constructs a network of linear optics, which can realize any quantum circuit diagram or quantum network based on the quantum circuit model. Quantum computing with continuous variables is also possible under the linear optics scheme.

The universality of 1- and 2-bit gates to implement arbitrary quantum computation has been proven. Up to ${\displaystyle N\times N}$ unitary matrix operations (${\displaystyle U(N)}$) can be realized by only using mirrors, beam splitters and phase shifters (this is also a starting point of boson sampling and of computational complexity analysis for LOQC). It points out that each ${\displaystyle U(N)}$ operator with ${\displaystyle N}$ inputs and ${\displaystyle N}$ outputs can be constructed via ${\displaystyle {\mathcal {O}}(N^{2})}$ linear optical elements. Based on the reason of universality and complexity, LOQC usually only uses mirrors, beam splitters, phase shifters and their combinations such as Mach-Zehnder interferometers with phase shifts to implement arbitrary quantum operators. If using a non-deterministic scheme, this fact also implies that LOQC could be resource-inefficient in terms of the number of optical elements and time steps needed to implement a certain quantum gate or circuit, which is a major drawback of LOQC.

Operations via linear optical elements (beam splitters, mirrors and phase shifters, in this case) preserve the photon statistics of input light. For example, a coherent (classical) light input produces a coherent light output; a superposition of quantum states input yields a quantum light state output. Due to this reason, people usually use single photon source case to analyze the effect of linear optical elements and operators. Multi-photon cases can be implied through some statistical transformations.

An intrinsic problem in using photons as information carriers is that photons hardly interact with each other. This potentially causes a scalability problem for LOQC, since nonlinear operations are hard to implement, which can increase the complexity of operators and hence can increase the resources required to realize a given computational function. One way to solve this problem is to bring nonlinear devices into the quantum network. For instance, the Kerr effect can be applied into LOQC to make a single-photon controlled-NOT and other operations.

KLM protocol

It was believed that adding nonlinearity to the linear optical network was sufficient to realize efficient quantum computation. However, to implement nonlinear optical effects is a difficult task. In 2000, Knill, Laflamme and Milburn proved that it is possible to create universal quantum computers solely with linear optical tools. Their work has become known as the "KLM scheme" or "KLM protocol", which uses linear optical elements, single photon sources and photon detectors as resources to construct a quantum computation scheme involving only ancilla resources, quantum teleportations and error corrections. It uses another way of efficient quantum computation with linear optical systems, and promotes nonlinear operations solely with linear optical elements.

At its root, the KLM scheme induces an effective interaction between photons by making projective measurements with photodetectors, which falls into the category of non-deterministic quantum computation. It is based on a non-linear sign shift between two qubits that uses two ancilla photons and post-selection. It is also based on the demonstrations that the probability of success of the quantum gates can be made close to one by using entangled states prepared non-deterministically and quantum teleportation with single-qubit operations. Otherwise, without a high enough success rate of a single quantum gate unit, it may require an exponential amount of computing resources. Meanwhile, the KLM scheme is based on the fact that proper quantum coding can reduce the resources for obtaining accurately encoded qubits efficiently with respect to the accuracy achieved, and can make LOQC fault-tolerant for photon loss, detector inefficiency and phase decoherence. As a result, LOQC can be robustly implemented through the KLM scheme with a low enough resource requirement to suggest practical scalability, making it as promising a technology for QIP as other known implementations.

Boson sampling

The more limited boson sampling model was suggested and analyzed by Aaronson and Arkhipov in 2013. It is not believed to be universal, but can still solve problems that are believed to be beyond the ability of classical computers, such as the boson sampling problem.

Elements of LOQC

DiVincenzo's criteria for quantum computation and QIP give that a universal system for QIP should satisfy at least the following requirements:

• a scalable physical system with well characterized qubits;
• the ability to initialize the state of the qubits to a simple fiducial state, such as ${\displaystyle |000\cdots \rangle }$;
• long relevant decoherence times, much longer than the gate operation time;
• a "universal" set of quantum gates (this requirement cannot be satisfied by a non-universal system);
• a qubit-specific measurement capability;
  if the system is also aiming for quantum communication, it should also satisfy at least the following two requirements;
• the ability to interconvert stationary and flying qubits; and
• the ability to faithfully transmit flying qubits between specified location.

As a result of using photons and linear optical circuits, in general LOQC systems can easily satisfy conditions 3, 6 and 7. The following sections mainly focus on the implementations of quantum information preparation, readout, manipulation, scalability and error corrections, in order to discuss the advantages and disadvantages of LOQC as a candidate for QIP

Qubits and modes

A qubit is one of the fundamental QIP units. A qubit state which can be represented by ${\displaystyle \alpha |0\rangle +\beta |1\rangle }$ is a superposition state which, if measured in the orthonormal basis ${\displaystyle \{|0\rangle ,|1\rangle \}}$, has probability ${\displaystyle |\alpha |^{2}}$ of being in the ${\displaystyle |0\rangle }$ state and probability ${\displaystyle |\beta |^{2}}$ of being in the ${\displaystyle |1\rangle }$ state, where ${\displaystyle |\alpha |^{2}+|\beta |^{2}=1}$ is the normalization condition. An optical mode is a distinguishable optical communication channel, which is usually labeled by subscripts of a quantum state. There are many ways to define distinguishable optical communication channels. For example, a set of modes could be different polarization of light which can be picked out with linear optical elements, various frequencies, or a combination of the two cases above.

In the KLM protocol, each of the photons is usually in one of two modes, and the modes are different between the photons (the possibility that a mode is occupied by more than one photon is zero). This is not the case only during implementations of controlled quantum gates such as CNOT. When the state of the system is as described, the photons can be distinguished, since they are in different modes, and therefore a qubit state can be represented using a single photon in two modes, vertical (V) and horizontal (H): for example, ${\displaystyle |0\rangle \equiv |0,1\rangle _{VH}}$ and ${\displaystyle |1\rangle \equiv |1,0\rangle _{VH}}$. It is common to refer to the states defined via occupation of modes as Fock states.

In boson sampling, photons are not distinguished, and therefore cannot directly represent the qubit state. Instead, we represent the qudit state of the entire quantum system by using the Fock states of ${\displaystyle M}$ modes which are occupied by ${\displaystyle N}$ indistinguishable single photons (this is a ${\displaystyle {\tbinom {M+N-1}{M}}}$-level quantum system).

State preparation

To prepare a desired multi-photon quantum state for LOQC, a single-photon state is first required. Therefore, non-linear optical elements, such as single-photon generators and some optical modules, will be employed. For example, optical parametric down-conversion can be used to conditionally generate the ${\displaystyle |1\rangle \equiv |1,0\rangle _{VH}}$ state in the vertical polarization channel at time ${\displaystyle t}$ (subscripts are ignored for this single qubit case). By using a conditional single-photon source, the output state is guaranteed, although this may require several attempts (depending on the success rate). A joint multi-qubit state can be prepared in a similar way. In general, an arbitrary quantum state can be generated for QIP with a proper set of photon sources.

Implementations of elementary quantum gates

To achieve universal quantum computing, LOQC should be capable of realizing a complete set of universal gates. This can be achieved in the KLM protocol but not in the boson sampling model.

Ignoring error correction and other issues, the basic principle in implementations of elementary quantum gates using only mirrors, beam splitters and phase shifters is that by using these linear optical elements, one can construct any arbitrary 1-qubit unitary operation; in other words, those linear optical elements support a complete set of operators on any single qubit.
The unitary matrix associated with a beam splitter ${\displaystyle \mathbf {B} _{\theta ,\phi }}$ is:

${\displaystyle U(\mathbf {B} _{\theta ,\phi })={\begin{bmatrix}\cos \theta &-e^{i\phi }\sin \theta \\e^{-i\phi }\sin \theta &\cos \theta \end{bmatrix}}}$,

where ${\displaystyle \theta }$ and ${\displaystyle \phi }$ are determined by the reflection amplitude ${\displaystyle r}$ and the transmission amplitude ${\displaystyle t}$ (relationship will be given later for a simpler case). For a symmetric beam splitter, which has a phase shift ${\displaystyle \phi ={\frac {\pi }{2}}}$ under the unitary transformation condition ${\displaystyle |t|^{2}+|r|^{2}=1}$ and ${\displaystyle t^{*}r+tr^{*}=0}$, one can show that

${\displaystyle U(\mathbf {B} _{\theta ,\phi ={\frac {\pi }{2}}})={\begin{bmatrix}t&r\\r&t\end{bmatrix}}={\begin{bmatrix}\cos \theta &-i\sin \theta \\-i\sin \theta &\cos \theta \end{bmatrix}}=\cos \theta {\hat {I}}-i\sin \theta {\hat {\sigma }}_{x}=e^{-i\theta {\hat {\sigma }}_{x}}}$,

which is a rotation of the single qubit state about the ${\displaystyle x}$-axis by ${\displaystyle 2\theta =2\cos ^{-1}(|t|)}$ in the Bloch sphere.

A mirror is a special case where the reflecting rate is 1, so that the corresponding unitary operator is a rotation matrix given by

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$.

For most cases of mirrors used in QIP, the incident angle ${\displaystyle \theta =45^{\circ }}$.

Similarly, a phase shifter operator ${\displaystyle \mathbf {P} _{\phi }}$ associates with a unitary operator described by ${\displaystyle U(\mathbf {P} _{\phi })=e^{i\phi }}$, or, if written in a 2-mode format

${\displaystyle U(\mathbf {P} _{\phi })={\begin{bmatrix}e^{i\phi }&0\\0&1\end{bmatrix}}={\begin{bmatrix}e^{i\phi /2}&0\\0&e^{-i\phi /2}\end{bmatrix}}{\text{(global phase ignored)}}=e^{i{\frac {\phi }{2}}{\hat {\sigma }}_{z}}}$,

which is equivalent to a rotation of ${\displaystyle -\phi }$ about the ${\displaystyle z}$-axis.

Since any two ${\displaystyle SU(2)}$ rotations along orthogonal rotating axes can generate arbitrary rotations in the Bloch sphere, one can use a set of symmetric beam splitters and mirrors to realize an arbitrary ${\displaystyle SU(2)}$ operators for QIP. The figures below are examples of implementing a Hadamard gate and a Pauli-X-gate (NOT gate) by using beam splitters (illustrated as rectangles connecting two sets of crossing lines with parameters ${\displaystyle \theta }$ and ${\displaystyle \phi }$) and mirrors (illustrated as rectangles connecting two sets of crossing lines with parameter ${\displaystyle R(\theta )}$).

Integrated photonic circuits for LOQC

In reality, assembling a whole bunch (possibly on the order of ${\displaystyle 10^{4}}$) of beam splitters and phase shifters in an optical experimental table is challenging and unrealistic. To make LOQC functional, useful and compact, one solution is to miniaturize all linear optical elements, photon sources and photon detectors, and to integrate them onto a chip. If using a semiconductor platform, single photon sources and photon detectors can be easily integrated. To separate modes, there have been integrated arrayed waveguide grating (AWG) which are commonly used as optical (de)multiplexers in wavelength division multiplexed (WDM). In principle, beam splitters and other linear optical elements can also be miniaturized or replaced by equivalent nanophotonics elements. Some progress in these endeavors can be found in the literature, for example, Refs. In 2013, the first integrated photonic circuit for quantum information processing has been demonstrated using photonic crystal waveguide to realize the interaction between guided field and atoms.

Implementations comparison

Comparison of the KLM protocol and the boson sampling model

The advantage of the KLM protocol over the boson sampling model is that while the KLM protocol is a universal model, boson sampling is not believed to be universal. On the other hand, it seems that the scalability issues in boson sampling are more manageable than those in the KLM protocol.

In boson sampling only a single measurement is allowed, a measurement of all the modes at the end of the computation. The only scalability problem in this model arises from the requirement that all the photons arrive at the photon detectors within a short-enough time interval and with close-enough frequencies.

In the KLM protocol, there are non-deterministic quantum gates, which are essential for the model to be universal. These rely on gate teleportation, where multiple probabilistic gates are prepared offline and additional measurements are performed mid-circuit. Those two factors are the cause for additional scalability problems in the KLM protocol.

In the KLM protocol the desired initial state is one in which each of the photons is in one of two modes, and the possibility that a mode is occupied by more than one photon is zero. In boson sampling, however, the desired initial state is specific, requiring that the first ${\displaystyle N}$ modes are each occupied by a single photon (${\displaystyle N}$ is the number of photons and ${\displaystyle M\geq N}$ is the number of modes) and all the other states are empty.

Earlier models

Another, earlier model which relies on the representation of several qubits by a single photon is based on the work of C. Adami and N. J. Cerf. By using both the location and the polarization of photons, a single photon in this model can represent several qubits; however, as a result, CNOT-gate can only be implemented between the two qubits represented by the same photon.


In the optical realization of the CNOT gate, the polarization and location are the control and target qubit, respectively.