A Medley of Potpourri

Sunday, August 6, 2023

Microwave transmission

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Microwave_transmission

Microwave transmission is the transmission of information by electromagnetic waves with wavelengths in the microwave frequency range of 300MHz to 300GHz(1 m - 1 mm wavelength) of the electromagnetic spectrum. Microwave signals are normally limited to the line of sight, so long-distance transmission using these signals requires a series of repeaters forming a microwave relay network. It is possible to use microwave signals in over-the-horizon communications using tropospheric scatter, but such systems are expensive and generally used only in specialist roles.

Although an experimental 40-mile (64 km) microwave telecommunication link across the English Channel was demonstrated in 1931, the development of radar in World War II provided the technology for practical exploitation of microwave communication. During the war, the British Army introduced the Wireless Set No. 10, which used microwave relays to multiplex eight telephone channels over long distances. A link across the English Channel allowed General Bernard Montgomery to remain in continual contact with his group headquarters in London.

In the post-war era, the development of microwave technology was rapid, which led to the construction of several transcontinental microwave relay systems in North America and Europe. In addition to carrying thousands of telephone calls at a time, these networks were also used to send television signals for cross-country broadcast, and later, computer data. Communication satellites took over the television broadcast market during the 1970s and 80s, and the introduction of long-distance fibre optic systems in the 1980s and especially 90s led to the rapid rundown of the relay networks, most of which are abandoned.

In recent years, there has been an explosive increase in use of the microwave spectrum by new telecommunication technologies such as wireless networks, and direct-broadcast satellites which broadcast television and radio directly into consumers' homes. Larger line-of-sight links are once again popular for handing connections between mobile telephone towers, although these are generally not organized into long relay chains.

Uses

Microwaves are widely used for point-to-point communications because their small wavelength allows conveniently-sized antennas to direct them in narrow beams, which can be pointed directly at the receiving antenna. This allows nearby microwave equipment to use the same frequencies without interfering with each other, as lower frequency radio waves do. This frequency reuse conserves scarce radio spectrum bandwidth. Another advantage is that the high frequency of microwaves gives the microwave band a very large information-carrying capacity; the microwave band has a bandwidth 30 times that of all the rest of the radio spectrum below it. A disadvantage is that microwaves are limited to line of sight propagation; they cannot pass around hills or mountains as lower frequency radio waves can.

Microwave radio transmission is commonly used in point-to-point communication systems on the surface of the Earth, in satellite communications, and in deep space radio communications. Other parts of the microwave radio band are used for radars, radio navigation systems, sensor systems, and radio astronomy.

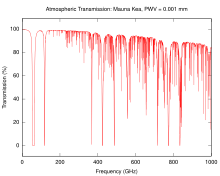
The next higher frequency band of the radio spectrum, between 30 GHz and 300 GHz, are called "millimeter waves" because their wavelengths range from 10 mm to 1 mm. Radio waves in this band are strongly attenuated by the gases of the atmosphere. This limits their practical transmission distance to a few kilometers, so these frequencies cannot be used for long-distance communication. The electronic technologies needed in the millimeter wave band are also in an earlier state of development than those of the microwave band.

Wireless transmission of information

One-way and two-way telecommunication using communications satellite
Terrestrial microwave relay links in telecommunications networks including backbone or backhaul carriers in cellular networks

More recently, microwaves have been used for wireless power transmission.

Microwave radio relay

Microwave radio relay is a technology widely used in the 1950s and 1960s for transmitting information, such as long-distance telephone calls and television programs between two terrestrial points on a narrow beam of microwaves. In microwave radio relay, a microwave transmitter and directional antenna transmits a narrow beam of microwaves carrying many channels of information on a line of sight path to another relay station where it is received by a directional antenna and receiver, forming a fixed radio connection between the two points. The link was often bidirectional, using a transmitter and receiver at each end to transmit data in both directions. The requirement of a line of sight limits the separation between stations to the visual horizon, about 30 to 50 miles (48 to 80 km). For longer distances, the receiving station could function as a relay, retransmitting the received information to another station along its journey. Chains of microwave relay stations were used to transmit telecommunication signals over transcontinental distances. Microwave relay stations were often located on tall buildings and mountaintops, with their antennas on towers to get maximum range.

Beginning in the 1950s, networks of microwave relay links, such as the AT&T Long Lines system in the U.S., carried long-distance telephone calls and television programs between cities. The first system, dubbed TDX and built by AT&T, connected New York and Boston in 1947 with a series of eight radio relay stations. Through the 1950s, they deployed a network of a slightly improved version across the U.S., known as TD2. These included long daisy-chained links that traversed mountain ranges and spanned continents. The launch of communication satellites in the 1970s provided a cheaper alternative. Much of the transcontinental traffic is now carried by satellites and optical fibers, but microwave relay remains important for shorter distances.

Planning

Because the radio waves travel in narrow beams confined to a line-of-sight path from one antenna to the other, they do not interfere with other microwave equipment, so nearby microwave links can use the same frequencies. Antennas must be highly directional (high gain); these antennas are installed in elevated locations such as large radio towers in order to be able to transmit across long distances. Typical types of antenna used in radio relay link installations are parabolic antennas, dielectric lens, and horn-reflector antennas, which have a diameter of up to 4 meters. Highly directive antennas permit an economical use of the available frequency spectrum, despite long transmission distances.

Because of the high frequencies used, a line-of-sight path between the stations is required. Additionally, in order to avoid attenuation of the beam, an area around the beam called the first Fresnel zone must be free from obstacles. Obstacles in the signal field cause unwanted attenuation. High mountain peak or ridge positions are often ideal.

In addition to conventional repeaters which use back-to-back radios transmitting on different frequencies, obstructions in microwave paths can be dealt with by using Passive repeater or on-frequency repeaters.

Obstacles, the curvature of the Earth, the geography of the area and reception issues arising from the use of nearby land (such as in manufacturing and forestry) are important issues to consider when planning radio links. In the planning process, it is essential that "path profiles" are produced, which provide information about the terrain and Fresnel zones affecting the transmission path. The presence of a water surface, such as a lake or river, along the path also must be taken into consideration since it can reflect the beam, and the direct and reflected beam can interfere at the receiving antenna, causing multipath fading. Multipath fades are usually deep only in a small spot and a narrow frequency band, so space and/or frequency diversity schemes can be applied to mitigate these effects.

The effects of atmospheric stratification cause the radio path to bend downward in a typical situation so a major distance is possible as the earth equivalent curvature increases from 6370 km to about 8500 km (a 4/3 equivalent radius effect). Rare events of temperature, humidity and pressure profile versus height, may produce large deviations and distortion of the propagation and affect transmission quality. High-intensity rain and snow making rain fade must also be considered as an impairment factor, especially at frequencies above 10 GHz. All previous factors, collectively known as path loss, make it necessary to compute suitable power margins, in order to maintain the link operative for a high percentage of time, like the standard 99.99% or 99.999% used in 'carrier class' services of most telecommunication operators.

The longest microwave radio relay known up to date crosses the Red Sea with a 360 km (200 mi) hop between Jebel Erba (2170m a.s.l., 20°44′46.17″N 36°50′24.65″E, Sudan) and Jebel Dakka (2572m a.s.l., 21°5′36.89″N 40°17′29.80″E, Saudi Arabia). The link was built in 1979 by Telettra to transmit 300 telephone channels and one TV signal, in the 2 GHz frequency band. (Hop distance is the distance between two microwave stations).

Previous considerations represent typical problems characterizing terrestrial radio links using microwaves for the so-called backbone networks: hop lengths of a few tens of kilometers (typically 10 to 60 km) were largely used until the 1990s. Frequency bands below 10 GHz, and above all, the information to be transmitted, were a stream containing a fixed capacity block. The target was to supply the requested availability for the whole block (Plesiochronous digital hierarchy, PDH, or synchronous digital hierarchy, SDH). Fading and/or multipath affecting the link for short time period during the day had to be counteracted by the diversity architecture. During 1990s microwave radio links begun widely to be used for urban links in cellular network. Requirements regarding link distance changed to shorter hops (less than 10 km, typically 3 to 5 km), and frequency increased to bands between 11 and 43 GHz and more recently, up to 86 GHz (E-band). Furthermore, link planning deals more with intense rainfall and less with multipath, so diversity schemes became less used. Another big change that occurred during the last decade was an evolution toward packet radio transmission. Therefore, new countermeasures, such as adaptive modulation, have been adopted.

The emitted power is regulated for cellular and microwave systems. These microwave transmissions use emitted power typically from 0.03 to 0.30 W, radiated by a parabolic antenna on a narrow beam diverging by a few degrees (1 to 3-4). The microwave channel arrangement is regulated by International Telecommunication Union (ITU-R) and local regulations (ETSI, FCC). In the last decade the dedicated spectrum for each microwave band has become extremely crowded, motivating the use of techniques to increase transmission capacity such as frequency reuse, polarization-division multiplexing, XPIC, MIMO.

History

The history of radio relay communication began in 1898 from the publication by Johann Mattausch in Austrian journal, Zeitschrift für Electrotechnik. But his proposal was primitive and not suitable for practical use. The first experiments with radio repeater stations to relay radio signals were done in 1899 by Emile Guarini-Foresio. However the low frequency and medium frequency radio waves used during the first 40 years of radio proved to be able to travel long distances by ground wave and skywave propagation. The need for radio relay did not really begin until the 1940s exploitation of microwaves, which traveled by line of sight and so were limited to a propagation distance of about 40 miles (64 km) by the visual horizon.

In 1931 an Anglo-French consortium headed by Andre C. Clavier demonstrated an experimental microwave relay link across the English Channel using 10-foot (3 m) dishes. Telephony, telegraph, and facsimile data was transmitted over the bidirectional 1.7 GHz beams 40 miles (64 km) between Dover, UK, and Calais, France. The radiated power, produced by a miniature Barkhausen–Kurz tube located at the dish's focus, was one-half watt. A 1933 military microwave link between airports at St. Inglevert, France, and Lympne, UK, a distance of 56 km (35 miles), was followed in 1935 by a 300 MHz telecommunication link, the first commercial microwave relay system.

The development of radar during World War II provided much of the microwave technology which made practical microwave communication links possible, particularly the klystron oscillator and techniques of designing parabolic antennas. Though not commonly known, the British Army used the Wireless Set Number 10 in this role during World War II.

After the war, telephone companies used this technology to build large microwave radio relay networks to carry long-distance telephone calls. During the 1950s a unit of the US telephone carrier, AT&T Long Lines, built a transcontinental system of microwave relay links across the US that grew to carry the majority of US long distance telephone traffic, as well as television network signals. The main motivation in 1946 to use microwave radio instead of cable was that a large capacity could be installed quickly and at less cost. It was expected at that time that the annual operating costs for microwave radio would be greater than for cable. There were two main reasons that a large capacity had to be introduced suddenly: Pent up demand for long-distance telephone service, because of the hiatus during the war years, and the new medium of television, which needed more bandwidth than radio. The prototype was called TDX and was tested with a connection between New York City and Murray Hill, the location of Bell Laboratories in 1946. The TDX system was set up between New York and Boston in 1947. The TDX was upgraded to the TD2 system, which used [the Morton tube, 416B and later 416C, manufactured by Western Electric] in the transmitters, and then later to TD3 that used solid-state electronics.

Remarkable were the microwave relay links to West Berlin during the Cold War, which had to be built and operated due to the large distance between West Germany and Berlin at the edge of the technical feasibility. In addition to the telephone network, also microwave relay links for the distribution of TV and radio broadcasts. This included connections from the studios to the broadcasting systems distributed across the country, as well as between the radio stations, for example for program exchange.

Military microwave relay systems continued to be used into the 1960s, when many of these systems were supplanted with tropospheric scatter or communication satellite systems. When the NATO military arm was formed, much of this existing equipment was transferred to communications groups. The typical communications systems used by NATO during that time period consisted of the technologies which had been developed for use by the telephone carrier entities in host countries. One example from the USA is the RCA CW-20A 1–2 GHz microwave relay system which utilized flexible UHF cable rather than the rigid waveguide required by higher frequency systems, making it ideal for tactical applications. The typical microwave relay installation or portable van had two radio systems (plus backup) connecting two line of sight sites. These radios would often carry 24 telephone channels frequency-division multiplexed on the microwave carrier (i.e. Lenkurt 33C FDM). Any channel could be designated to carry up to 18 teletype communications instead. Similar systems from Germany and other member nations were also in use.

Long-distance microwave relay networks were built in many countries until the 1980s, when the technology lost its share of fixed operation to newer technologies such as fiber-optic cable and communication satellites, which offer a lower cost per bit.

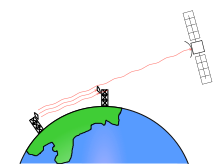
During the Cold War, the US intelligence agencies, such as the National Security Agency (NSA), were reportedly able to intercept Soviet microwave traffic using satellites such as Rhyolite. Much of the beam of a microwave link passes the receiving antenna and radiates toward the horizon, into space. By positioning a geosynchronous satellite in the path of the beam, the microwave beam can be received.

At the turn of the century, microwave radio relay systems are being used increasingly in portable radio applications. The technology is particularly suited to this application because of lower operating costs, a more efficient infrastructure, and provision of direct hardware access to the portable radio operator.

Microwave link

A microwave link is a communications system that uses a beam of radio waves in the microwave frequency range to transmit video, audio, or data between two locations, which can be from just a few feet or meters to several miles or kilometers apart. Microwave links are commonly used by television broadcasters to transmit programmes across a country, for instance, or from an outside broadcast back to a studio.

Mobile units can be camera mounted, allowing cameras the freedom to move around without trailing cables. These are often seen on the touchlines of sports fields on Steadicam systems.

Properties of microwave links

Involve line of sight (LOS) communication technology
Affected greatly by environmental constraints, including rain fade
Have very limited penetration capabilities through obstacles such as hills, buildings and trees
Sensitive to high pollen count
Signals can be degraded during Solar proton events

Uses of microwave links

In communications between satellites and base stations
As backbone carriers for cellular systems
In short-range indoor communications
Linking remote and regional telephone exchanges to larger (main) exchanges without the need for copper/optical fibre lines
Measuring the intensity of rain between two locations

Troposcatter

Terrestrial microwave relay links are limited in distance to the visual horizon, a few tens of miles or kilometers depending on tower height. Tropospheric scatter ("troposcatter" or "scatter") was a technology developed in the 1950s to allow microwave communication links beyond the horizon, to a range of several hundred kilometers. The transmitter radiates a beam of microwaves into the sky, at a shallow angle above the horizon toward the receiver. As the beam passes through the troposphere a small fraction of the microwave energy is scattered back toward the ground by water vapor and dust in the air. A sensitive receiver beyond the horizon picks up this reflected signal. Signal clarity obtained by this method depends on the weather and other factors, and as a result, a high level of technical difficulty is involved in the creation of a reliable over horizon radio relay link. Troposcatter links are therefore only used in special circumstances where satellites and other long-distance communication channels cannot be relied on, such as in military communications.

H-theorem

https://en.wikipedia.org/wiki/H-theorem

From Wikipedia, the free encyclopedia

In classical statistical mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency to decrease in the quantity H (defined below) in a nearly-ideal gas of molecules. As this quantity H was meant to represent the entropy of thermodynamics, the H-theorem was an early demonstration of the power of statistical mechanics as it claimed to derive the second law of thermodynamics—a statement about fundamentally irreversible processes—from reversible microscopic mechanics. It is thought to prove the second law of thermodynamics, albeit under the assumption of low-entropy initial conditions.

The H-theorem is a natural consequence of the kinetic equation derived by Boltzmann that has come to be known as Boltzmann's equation. The H-theorem has led to considerable discussion about its actual implications, with major themes being:

What is entropy? In what sense does Boltzmann's quantity H correspond to the thermodynamic entropy?
Are the assumptions (especially the assumption of molecular chaos) behind Boltzmann's equation too strong? When are these assumptions violated?

Name and pronunciation

Boltzmann in his original publication writes the symbol E (as in entropy) for its statistical function. Years later, Samuel Hawksley Burbury, one of the critics of the theorem, wrote the function with the symbol H, a notation that was subsequently adopted by Boltzmann when referring to his "H-theorem". The notation has led to some confusion regarding the name of the theorem. Even though the statement is usually referred to as the "Aitch theorem", sometimes it is instead called the "Eta theorem", as the capital Greek letter Eta (Η) is undistinguishable from the capital version of Latin letter h (H). Discussions have been raised on how the symbol should be understood, but it remains unclear due to the lack of written sources from the time of the theorem. Studies of the typography and the work of J.W. Gibbs seem to favour the interpretation of H as Eta.

Definition and meaning of Boltzmann's H

The H value is determined from the function f(E, t) dE, which is the energy distribution function of molecules at time t. The value f(E, t) dE is the number of molecules that have kinetic energy between E and E + dE. H itself is defined as

H (t) = \int_{0}^{\infty} f (E, t) (\ln \frac{f (E, t)}{\sqrt{E}} - 1) d E .

For an isolated ideal gas (with fixed total energy and fixed total number of particles), the function H is at a minimum when the particles have a Maxwell–Boltzmann distribution; if the molecules of the ideal gas are distributed in some other way (say, all having the same kinetic energy), then the value of H will be higher. Boltzmann's H-theorem, described in the next section, shows that when collisions between molecules are allowed, such distributions are unstable and tend to irreversibly seek towards the minimum value of H (towards the Maxwell–Boltzmann distribution).

(Note on notation: Boltzmann originally used the letter E for quantity H; most of the literature after Boltzmann uses the letter H as here. Boltzmann also used the symbol x to refer to the kinetic energy of a particle.)

Boltzmann's H theorem

Boltzmann considered what happens during the collision between two particles. It is a basic fact of mechanics that in the elastic collision between two particles (such as hard spheres), the energy transferred between the particles varies depending on initial conditions (angle of collision, etc.).

Boltzmann made a key assumption known as the Stosszahlansatz (molecular chaos assumption), that during any collision event in the gas, the two particles participating in the collision have 1) independently chosen kinetic energies from the distribution, 2) independent velocity directions, 3) independent starting points. Under these assumptions, and given the mechanics of energy transfer, the energies of the particles after the collision will obey a certain new random distribution that can be computed.

Considering repeated uncorrelated collisions, between any and all of the molecules in the gas, Boltzmann constructed his kinetic equation (Boltzmann's equation). From this kinetic equation, a natural outcome is that the continual process of collision causes the quantity H to decrease until it has reached a minimum.

Impact

Although Boltzmann's H-theorem turned out not to be the absolute proof of the second law of thermodynamics as originally claimed (see Criticisms below), the H-theorem led Boltzmann in the last years of the 19th century to more and more probabilistic arguments about the nature of thermodynamics. The probabilistic view of thermodynamics culminated in 1902 with Josiah Willard Gibbs's statistical mechanics for fully general systems (not just gases), and the introduction of generalized statistical ensembles.

The kinetic equation and in particular Boltzmann's molecular chaos assumption inspired a whole family of Boltzmann equations that are still used today to model the motions of particles, such as the electrons in a semiconductor. In many cases the molecular chaos assumption is highly accurate, and the ability to discard complex correlations between particles makes calculations much simpler.

The process of thermalisation can be described using the H-theorem or the relaxation theorem.

Criticism and exceptions

There are several notable reasons described below why the H-theorem, at least in its original 1871 form, is not completely rigorous. As Boltzmann would eventually go on to admit, the arrow of time in the H-theorem is not in fact purely mechanical, but really a consequence of assumptions about initial conditions.

Loschmidt's paradox

Soon after Boltzmann published his H theorem, Johann Josef Loschmidt objected that it should not be possible to deduce an irreversible process from time-symmetric dynamics and a time-symmetric formalism. If the H decreases over time in one state, then there must be a matching reversed state where H increases over time (Loschmidt's paradox). The explanation is that Boltzmann's equation is based on the assumption of "molecular chaos", i.e., that it follows from, or at least is consistent with, the underlying kinetic model that the particles be considered independent and uncorrelated. It turns out that this assumption breaks time reversal symmetry in a subtle sense, and therefore begs the question. Once the particles are allowed to collide, their velocity directions and positions in fact do become correlated (however, these correlations are encoded in an extremely complex manner). This shows that an (ongoing) assumption of independence is not consistent with the underlying particle model.

Boltzmann's reply to Loschmidt was to concede the possibility of these states, but noting that these sorts of states were so rare and unusual as to be impossible in practice. Boltzmann would go on to sharpen this notion of the "rarity" of states, resulting in his famous equation, his entropy formula of 1877 (see Boltzmann's entropy formula).

Spin echo

As a demonstration of Loschmidt's paradox, a famous modern counter example (not to Boltzmann's original gas-related H-theorem, but to a closely related analogue) is the phenomenon of spin echo. In the spin echo effect, it is physically possible to induce time reversal in an interacting system of spins.

An analogue to Boltzmann's H for the spin system can be defined in terms of the distribution of spin states in the system. In the experiment, the spin system is initially perturbed into a non-equilibrium state (high H), and, as predicted by the H theorem the quantity H soon decreases to the equilibrium value. At some point, a carefully constructed electromagnetic pulse is applied that reverses the motions of all the spins. The spins then undo the time evolution from before the pulse, and after some time the H actually increases away from equilibrium (once the evolution has completely unwound, the H decreases once again to the minimum value). In some sense, the time reversed states noted by Loschmidt turned out to be not completely impractical.

Poincaré recurrence

In 1896, Ernst Zermelo noted a further problem with the H theorem, which was that if the system's H is at any time not a minimum, then by Poincaré recurrence, the non-minimal H must recur (though after some extremely long time). Boltzmann admitted that these recurring rises in H technically would occur, but pointed out that, over long times, the system spends only a tiny fraction of its time in one of these recurring states.

The second law of thermodynamics states that the entropy of an isolated system always increases to a maximum equilibrium value. This is strictly true only in the thermodynamic limit of an infinite number of particles. For a finite number of particles, there will always be entropy fluctuations. For example, in the fixed volume of the isolated system, the maximum entropy is obtained when half the particles are in one half of the volume, half in the other, but sometimes there will be temporarily a few more particles on one side than the other, and this will constitute a very small reduction in entropy. These entropy fluctuations are such that the longer one waits, the larger an entropy fluctuation one will probably see during that time, and the time one must wait for a given entropy fluctuation is always finite, even for a fluctuation to its minimum possible value. For example, one might have an extremely low entropy condition of all particles being in one half of the container. The gas will quickly attain its equilibrium value of entropy, but given enough time, this same situation will happen again. For practical systems, e.g. a gas in a 1-liter container at room temperature and atmospheric pressure, this time is truly enormous, many multiples of the age of the universe, and, practically speaking, one can ignore the possibility.

Fluctuations of H in small systems

Since H is a mechanically defined variable that is not conserved, then like any other such variable (pressure, etc.) it will show thermal fluctuations. This means that H regularly shows spontaneous increases from the minimum value. Technically this is not an exception to the H theorem, since the H theorem was only intended to apply for a gas with a very large number of particles. These fluctuations are only perceptible when the system is small and the time interval over which it is observed is not enormously large.

If H is interpreted as entropy as Boltzmann intended, then this can be seen as a manifestation of the fluctuation theorem.

Connection to information theory

H is a forerunner of Shannon's information entropy. Claude Shannon denoted his measure of information entropy H after the H-theorem. The article on Shannon's information entropy contains an explanation of the discrete counterpart of the quantity H, known as the information entropy or information uncertainty (with a minus sign). By extending the discrete information entropy to the continuous information entropy, also called differential entropy, one obtains the expression in the equation from the section above, Definition and Meaning of Boltzmann's H, and thus a better feel for the meaning of H.

The H-theorem's connection between information and entropy plays a central role in a recent controversy called the Black hole information paradox.

Tolman's H-theorem

Richard C. Tolman's 1938 book The Principles of Statistical Mechanics dedicates a whole chapter to the study of Boltzmann's H theorem, and its extension in the generalized classical statistical mechanics of Gibbs. A further chapter is devoted to the quantum mechanical version of the H-theorem.

Classical mechanical

We let $q i$ and $p i$ be our generalized coordinates for a set of $r$ particles. Then we consider a function $f$ that returns the probability density of particles, over the states in phase space. Note how this can be multiplied by a small region in phase space, denoted by $δ q_{1} . . . δ p_{r}$ , to yield the (average) expected number of particles in that region.

δ n = f (q_{1} . . . p_{r}, t) δ q_{1} δ p_{1} . . . δ q_{r} δ p_{r} .

Tolman offers the following equations for the definition of the quantity H in Boltzmann's original H theorem.

H = \sum_{i} f_{i} \ln f_{i} δ q_{1} \dots δ p_{r}

Here we sum over the regions into which phase space is divided, indexed by $i$ . And in the limit for an infinitesimal phase space volume $δ q_{i} \to 0, δ p_{i} \to 0 \forall i$ , we can write the sum as an integral.

H = \int \dots \int f \ln f d q_{1} \dots d p_{r}

H can also be written in terms of the number of molecules present in each of the cells.

\begin{aligned} H & = \sum (n_{i} \ln n_{i} - n_{i} \ln δ v_{γ}) \\ = \sum n_{i} \ln n_{i} + constant \end{aligned}

An additional way to calculate the quantity H is:

H = - \ln P + constant

where P is the probability of finding a system chosen at random from the specified microcanonical ensemble. It can finally be written as:

H = - \ln G + constant

where G is the number of classical states.

The quantity H can also be defined as the integral over velocity space:

$H \overset{d e f}{=} \int P (\ln P) d^{3} v = ⟨ \ln P ⟩$

(1)

where P(v) is the probability distribution.

Using the Boltzmann equation one can prove that H can only decrease.

For a system of N statistically independent particles, H is related to the thermodynamic entropy S through:

S \overset{d e f}{=} - V k H + constant

So, according to the H-theorem, S can only increase.

Quantum mechanical

In quantum statistical mechanics (which is the quantum version of classical statistical mechanics), the H-function is the function:

H = \sum_{i} p_{i} \ln p_{i},

where summation runs over all possible distinct states of the system, and p_i is the probability that the system could be found in the i-th state.

This is closely related to the entropy formula of Gibbs,

S = - k \sum_{i} p_{i} \ln p_{i}

and we shall (following e.g., Waldram (1985), p. 39) proceed using S rather than H.

First, differentiating with respect to time gives

\begin{aligned} \frac{d S}{d t} & = - k \sum_{i} (\frac{d p_{i}}{d t} \ln p_{i} + \frac{d p_{i}}{d t}) \\ = - k \sum_{i} \frac{d p_{i}}{d t} \ln p_{i} \end{aligned}

(using the fact that Σ dp_i/dt = 0, since Σ p_i = 1, so the second term vanishes. We will see later that it will be useful to break this into two sums.)

Now Fermi's golden rule gives a master equation for the average rate of quantum jumps from state α to β; and from state β to α. (Of course, Fermi's golden rule itself makes certain approximations, and the introduction of this rule is what introduces irreversibility. It is essentially the quantum version of Boltzmann's Stosszahlansatz.) For an isolated system the jumps will make contributions

\begin{aligned} \frac{d p_{α}}{d t} & = \sum_{β} ν_{α β} (p_{β} - p_{α}) \\ \frac{d p_{β}}{d t} & = \sum_{α} ν_{α β} (p_{α} - p_{β}) \end{aligned}

where the reversibility of the dynamics ensures that the same transition constant ν_αβ appears in both expressions.

\frac{d S}{d t} = \frac{1}{2} k \sum_{α, β} ν_{α β} (\ln p_{β} - \ln p_{α}) (p_{β} - p_{α}) .

The two differences terms in the summation always have the same sign. For example:

\begin{aligned} w_{β} < w_{α} \end{aligned}

then

\begin{aligned} \ln w_{β} < \ln w_{α} \end{aligned}

so overall the two negative signs will cancel.

Therefore,

Δ S \geq 0

for an isolated system.

The same mathematics is sometimes used to show that relative entropy is a Lyapunov function of a Markov process in detailed balance, and other chemistry contexts.

Gibbs' H-theorem

Evolution of an ensemble of classical systems in phase space (top). Each system consists of one massive particle in a one-dimensional potential well (red curve, lower figure). The initially compact ensemble becomes swirled up over time.

Josiah Willard Gibbs described another way in which the entropy of a microscopic system would tend to increase over time. Later writers have called this "Gibbs' H-theorem" as its conclusion resembles that of Boltzmann's. Gibbs himself never called it an H-theorem, and in fact his definition of entropy—and mechanism of increase—are very different from Boltzmann's. This section is included for historical completeness.

The setting of Gibbs' entropy production theorem is in ensemble statistical mechanics, and the entropy quantity is the Gibbs entropy (information entropy) defined in terms of the probability distribution for the entire state of the system. This is in contrast to Boltzmann's H defined in terms of the distribution of states of individual molecules, within a specific state of the system.

Gibbs considered the motion of an ensemble which initially starts out confined to a small region of phase space, meaning that the state of the system is known with fair precision though not quite exactly (low Gibbs entropy). The evolution of this ensemble over time proceeds according to Liouville's equation. For almost any kind of realistic system, the Liouville evolution tends to "stir" the ensemble over phase space, a process analogous to the mixing of a dye in an incompressible fluid. After some time, the ensemble appears to be spread out over phase space, although it is actually a finely striped pattern, with the total volume of the ensemble (and its Gibbs entropy) conserved. Liouville's equation is guaranteed to conserve Gibbs entropy since there is no random process acting on the system; in principle, the original ensemble can be recovered at any time by reversing the motion.

The critical point of the theorem is thus: If the fine structure in the stirred-up ensemble is very slightly blurred, for any reason, then the Gibbs entropy increases, and the ensemble becomes an equilibrium ensemble. As to why this blurring should occur in reality, there are a variety of suggested mechanisms. For example, one suggested mechanism is that the phase space is coarse-grained for some reason (analogous to the pixelization in the simulation of phase space shown in the figure). For any required finite degree of fineness the ensemble becomes "sensibly uniform" after a finite time. Or, if the system experiences a tiny uncontrolled interaction with its environment, the sharp coherence of the ensemble will be lost. Edwin Thompson Jaynes argued that the blurring is subjective in nature, simply corresponding to a loss of knowledge about the state of the system. In any case, however it occurs, the Gibbs entropy increase is irreversible provided the blurring cannot be reversed.

Quantum phase space dynamics in the same potential, visualized with the Wigner quasiprobability distribution. The lower image shows the equilibrated (time-averaged) distribution, with an entropy that is +1.37k higher.

The exactly evolving entropy, which does not increase, is known as fine-grained entropy. The blurred entropy is known as coarse-grained entropy. Leonard Susskind analogizes this distinction to the notion of the volume of a fibrous ball of cotton: On one hand the volume of the fibers themselves is constant, but in another sense there is a larger coarse-grained volume, corresponding to the outline of the ball.

Gibbs' entropy increase mechanism solves some of the technical difficulties found in Boltzmann's H-theorem: The Gibbs entropy does not fluctuate nor does it exhibit Poincare recurrence, and so the increase in Gibbs entropy, when it occurs, is therefore irreversible as expected from thermodynamics. The Gibbs mechanism also applies equally well to systems with very few degrees of freedom, such as the single-particle system shown in the figure. To the extent that one accepts that the ensemble becomes blurred, then, Gibbs' approach is a cleaner proof of the second law of thermodynamics.

Unfortunately, as pointed out early on in the development of quantum statistical mechanics by John von Neumann and others, this kind of argument does not carry over to quantum mechanics. In quantum mechanics, the ensemble cannot support an ever-finer mixing process, because of the finite dimensionality of the relevant portion of Hilbert space. Instead of converging closer and closer to the equilibrium ensemble (time-averaged ensemble) as in the classical case, the density matrix of the quantum system will constantly show evolution, even showing recurrences. Developing a quantum version of the H-theorem without appeal to the Stosszahlansatz is thus significantly more complicated.