Bomb

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Bomb

An iron grenade with a wooden fuse from 1580

A bomb is an explosive weapon that uses the exothermic reaction of an explosive material to provide an extremely sudden and violent release of energy. Detonations inflict damage principally through ground- and atmosphere-transmitted mechanical stress, the impact and penetration of pressure-driven projectiles, pressure damage, and explosion-generated effects. Bombs have been utilized since the 11th century starting in East Asia.

The term bomb is not usually applied to explosive devices used for civilian purposes such as construction or mining, although the people using the devices may sometimes refer to them as a "bomb". The military use of the term "bomb", or more specifically aerial bomb action, typically refers to airdropped, unpowered explosive weapons most commonly used by air forces and naval aviation. Other military explosive weapons not classified as "bombs" include shells, depth charges (used in water), or land mines. In unconventional warfare, other names can refer to a range of offensive weaponry. For instance, in recent Middle Eastern conflicts, homemade bombs called "improvised explosive devices" (IEDs) have been employed by insurgent fighters to great effectiveness.

The word comes from the Latin bombus, which in turn comes from the Greek βόμβος romanized bombos, an onomatopoetic term meaning 'booming', 'buzzing'.

A "wind-and-dust" bomb depicted in the Ming Dynasty book Huolongjing. The pot contains a tube of gunpowder, and was thrown at invaders.

History

See also: History of gunpowder

An illustration depicting bombs thrown at Manchu assault ladders during the siege of Ningyuan, from the book Thai Tsu Shih Lu Thu (Veritable Records of the Great Ancestor) written in 1635. The bombs are known as "thunder crash bombs."

Explosive bombs were used in East Asia in 1221, by a Jurchen Jin army against a Chinese Song city. Bombs built using bamboo tubes appear in the 11th century. Bombs made of cast iron shells packed with explosive gunpowder date to 13th century China. The term was coined for this bomb (i.e. "thunder-crash bomb") during a Jin dynasty (1115–1234) naval battle of 1231 against the Mongols.

Thunder crash bombs from the Mongol invasions of Japan (13th century) that were excavated from a shipwreck near the Liancourt Rocks

The History of Jin 《金史》 (compiled by 1345) states that in 1232, as the Mongol general Subutai (1176–1248) descended on the Jin stronghold of Kaifeng, the defenders had a "thunder crash bomb" which "consisted of gunpowder put into an iron container ... then when the fuse was lit (and the projectile shot off) there was a great explosion the noise whereof was like thunder, audible for more than thirty miles, and the vegetation was scorched and blasted by the heat over an area of more than half a mou. When hit, even iron armour was quite pierced through."

The Song Dynasty (960–1279) official Li Zengbo wrote in 1257 that arsenals should have several hundred thousand iron bomb shells available and that when he was in Jingzhou, about one to two thousand were produced each month for dispatch of ten to twenty thousand at a time to Xiangyang and Yingzhou. The Ming Dynasty text Huolongjing describes the use of poisonous gunpowder bombs, including the "wind-and-dust" bomb.

During the Mongol invasions of Japan, the Mongols used the explosive "thunder-crash bombs" against the Japanese. Archaeological evidence of the "thunder-crash bombs" has been discovered in an underwater shipwreck off the shore of Japan by the Kyushu Okinawa Society for Underwater Archaeology. X-rays by Japanese scientists of the excavated shells confirmed that they contained gunpowder.

Shock

Explosive shock waves can cause situations such as body displacement (i.e., people being thrown through the air), dismemberment, internal bleeding and ruptured eardrums.

Shock waves produced by explosive events have two distinct components, the positive and negative wave. The positive wave shoves outward from the point of detonation, followed by the trailing vacuum space "sucking back" towards the point of origin as the shock bubble collapses. The greatest defense against shock injuries is distance from the source of shock. As a point of reference, the overpressure at the Oklahoma City bombing was estimated in the range of 28 MPa.

Heat

A thermal wave is created by the sudden release of heat caused by an explosion. Military bomb tests have documented temperatures of up to 2,480 °C (4,500 °F). While capable of inflicting severe to catastrophic burns and causing secondary fires, thermal wave effects are considered very limited in range compared to shock and fragmentation. This rule has been challenged, however, by military development of thermobaric weapons, which employ a combination of negative shock wave effects and extreme temperature to incinerate objects within the blast radius.

Fragmentation

Main article: Fragmentation (weaponry)

An illustration of a fragmentation bomb from the 14th century Ming Dynasty text Huolongjing. The black dots represent iron pellets.

Fragmentation is produced by the acceleration of shattered pieces of bomb casing and adjacent physical objects. The use of fragmentation in bombs dates to the 14th century, and appears in the Ming Dynasty text Huolongjing. The fragmentation bombs were filled with iron pellets and pieces of broken porcelain. Once the bomb explodes, the resulting fragments are capable of piercing the skin and blinding enemy soldiers.

While conventionally viewed as small metal shards moving at super-supersonic and hypersonic speeds, fragmentation can occur in epic proportions and travel for extensive distances. When the SS Grandcamp exploded in the Texas City Disaster on April 16, 1947, one fragment of that blast was a two-ton anchor which was hurled nearly two miles inland to embed itself in the parking lot of the Pan American refinery.

Effects on living things

To people who are close to a blast incident, such as bomb disposal technicians, soldiers wearing body armor, deminers, or individuals wearing little to no protection, there are four types of blast effects on the human body: overpressure (shock), fragmentation, impact, and heat. Overpressure refers to the sudden and drastic rise in ambient pressure that can damage the internal organs, possibly leading to permanent damage or death. Fragmentation can also include sand, debris and vegetation from the area surrounding the blast source. This is very common in anti-personnel mine blasts. The projection of materials poses a potentially lethal threat caused by cuts in soft tissues, as well as infections, and injuries to the internal organs. When the overpressure wave impacts the body it can induce violent levels of blast-induced acceleration. Resulting injuries may range from minor to unsurvivable. Immediately following this initial acceleration, deceleration injuries can occur when a person impacts directly against a rigid surface or obstacle after being set in motion by the force of the blast. Finally, injury and fatality can result from the explosive fireball as well as incendiary agents projected onto the body. Personal protective equipment, such as a bomb suit or demining ensemble, as well as helmets, visors and foot protection, can dramatically reduce the four effects, depending upon the charge, proximity and other variables.

Types

Diagram of a simple time bomb in the form of a pipe bom

An American B61 nuclear bomb on its loading carriage

Unexploded unguided aerial bomb with contact fuse used by the Portuguese Air Force, Guinea-Bissau War of Independence, March 1974.

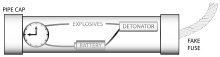
Experts commonly distinguish between civilian and military bombs. The latter are almost always mass-produced weapons, developed and constructed to a standard design out of standard components and intended to be deployed in a standard explosive device. IEDs are divided into three basic categories by basic size and delivery. Type 76, IEDs are hand-carried parcel or suitcase bombs, type 80, are "suicide vests" worn by a bomber, and type 3 devices are vehicles laden with explosives to act as large-scale stationary or self-propelled bombs, also known as VBIED (vehicle-borne IEDs).

Improvised explosive materials are typically unstable and subject to spontaneous, unintentional detonation triggered by a wide range of environmental effects, ranging from impact and friction to electrostatic shock. Even subtle motion, change in temperature, or the nearby use of cellphones or radios can trigger an unstable or remote-controlled device. Any interaction with explosive materials or devices by unqualified personnel should be considered a grave and immediate risk of death or dire injury. The safest response to finding an object believed to be an explosive device is to get as far away from it as possible.

Atomic bombs are based on the theory of nuclear fission, that when a large atom splits, it releases a massive amount of energy. Thermonuclear weapons, (colloquially known as "hydrogen bombs") use the energy from an initial fission explosion to create an even more powerful fusion explosion.

The term "dirty bomb" refers to a specialized device that relies on a comparatively low explosive yield to scatter harmful material over a wide area. Most commonly associated with radiological or chemical materials, dirty bombs seek to kill or injure and then to deny access to a contaminated area until a thorough clean-up can be accomplished. In the case of urban settings, this clean-up may take extensive time, rendering the contaminated zone virtually uninhabitable in the interim.

The power of large bombs is typically measured in kilotons (kt) or megatons of TNT (Mt). The most powerful bombs ever used in combat were the two atomic bombs dropped by the United States to attack Hiroshima and Nagasaki, and the most powerful ever tested was the Tsar Bomba. The most powerful non-nuclear bomb is Russian "Father of All Bombs" (officially Aviation Thermobaric Bomb of Increased Power (ATBIP)) followed by the United States Air Force's MOAB (officially Massive Ordnance Air Blast, or more commonly known as the "Mother of All Bombs").

Below is a list of five different types of bombs based on the fundamental explosive mechanism they employ.

Compressed gas

Relatively small explosions can be produced by pressurizing a container until catastrophic failure such as with a dry ice bomb. Technically, devices that create explosions of this type can not be classified as "bombs" by the definition presented at the top of this article. However, the explosions created by these devices can cause property damage, injury, or death. Flammable liquids, gasses and gas mixtures dispersed in these explosions may also ignite if exposed to a spark or flame.

Low explosive

The simplest and oldest bombs store energy in the form of a low explosive. Black powder is an example of a low explosive. Low explosives typically consist of a mixture of an oxidizing salt, such as potassium nitrate (saltpeter), with solid fuel, such as charcoal or aluminium powder. These compositions deflagrate upon ignition, producing hot gas. Under normal circumstances, this deflagration occurs too slowly to produce a significant pressure wave; low explosives, therefore, must generally be used in large quantities or confined in a container with a high burst pressure to be useful as a bomb.

High explosive

A high explosive bomb is one that employs a process called "detonation" to rapidly go from an initially high energy molecule to a very low energy molecule. Detonation is distinct from deflagration in that the chemical reaction propagates faster than the speed of sound (often many times faster) in an intense shock wave. Therefore, the pressure wave produced by a high explosive is not significantly increased by confinement as detonation occurs so quickly that the resulting plasma does not expand much before all the explosive material has reacted. This has led to the development of plastic explosive. A casing is still employed in some high explosive bombs, but with the purpose of fragmentation. Most high explosive bombs consist of an insensitive secondary explosive that must be detonated with a blasting cap containing a more sensitive primary explosive.

Thermobaric

A thermobaric bomb is a type of explosive that utilizes oxygen from the surrounding air to generate an intense, high-temperature explosion, and in practice the blast wave typically produced by such a weapon is of a significantly longer duration than that produced by a conventional condensed explosive. The fuel-air bomb is one of the best-known types of thermobaric weapons.

Nuclear fission

Nuclear fission type atomic bombs utilize the energy present in very heavy atomic nuclei, such as U-235 or Pu-239. In order to release this energy rapidly, a certain amount of the fissile material must be very rapidly consolidated while being exposed to a neutron source. If consolidation occurs slowly, repulsive forces drive the material apart before a significant explosion can occur. Under the right circumstances, rapid consolidation can provoke a chain reaction that can proliferate and intensify by many orders of magnitude within microseconds. The energy released by a nuclear fission bomb may be tens of thousands of times greater than a chemical bomb of the same mass.

Nuclear fusion

A thermonuclear weapon is a type of nuclear bomb that releases energy through the combination of fission and fusion of the light atomic nuclei of deuterium and tritium. With this type of bomb, a thermonuclear detonation is triggered by the detonation of a fission type nuclear bomb contained within a material containing high concentrations of deuterium and tritium. Weapon yield is typically increased with a tamper that increases the duration and intensity of the reaction through inertial confinement and neutron reflection. Nuclear fusion bombs can have arbitrarily high yields making them hundreds or thousands of times more powerful than nuclear fission.

A pure fusion weapon is a hypothetical nuclear weapon that does not require a primary fission stage to start a fusion reaction.

Antimatter

Antimatter bombs can theoretically be constructed, but antimatter is very costly to produce and hard to store safely.

Other

• Aerial bomb – designed to be dropped from a military aircraft (or even any aircraft) and carried on hardpoints or in bomb bays
• Delay-action bomb – explodes some time after impact, as opposed to before or on impact
• Dummy bomb – harmless bomb that has been fully disabled or has had its explosive contents removed, often used for training or display
• Glide bomb – features flight control surfaces, allowing it to glide fairly long distances to its target
• General-purpose bomb – aerial bomb dropped for multiple purposes, and thus designed to suit multiple purposes
• Incendiary bomb – designed to set targets ablaze
• Cluster bomb – releases additional submunitions, often smaller bombs, upon detonation
• Anti-runway penetration bomb – designed to destroy runways and aprons
• Bunker buster – capable of penetrating hardened or fortified surfaces before detonating
• Concrete bomb – contains dense, inert material (typically concrete) instead of explosives, using the kinetic energy of the falling bomb to destroy target
• Improvised explosive device – classification of bombs produced in unconventional ways or using unconventional materials; includes explosives such as the barrel bomb, nail bomb, pipe bomb, pressure cooker bomb, fertilizer bomb, and Molotov cocktail

Delivery

A B-2 Spirit drops forty-seven 500 lb (230 kg) class Mark 82 bombs (little more than half a B-2's maximum total ordnance payload) in a 1994 live fire exercise in California

A United States National Guard soldier firing a 40 mm grenade from an M320 grenade launcher

Destruction caused by Soviet bombing during the Continuation War in Helsinki, Finland, the night of February 6–7, 1944

The first air-dropped bombs were used by the Austrians in the 1849 siege of Venice. Two hundred unmanned balloons carried small bombs, although few bombs actually hit the city.

The first bombing from a fixed-wing aircraft took place in 1911 when the Italians dropped bombs by hand on the Turkish lines in what is now Libya, during the Italo-Turkish War. The first large scale dropping of bombs took place during World War I starting in 1915 with the German Zeppelin airship raids on London, England, and the same war saw the invention of the first heavy bombers. One Zeppelin raid on 8 September 1915 dropped 4,000 lb (1,800 kg) of high explosives and incendiary bombs, including one bomb that weighed 600 lb (270 kg).

During World War II bombing became a major military feature, and a number of novel delivery methods were introduced. These included Barnes Wallis's bouncing bomb, designed to bounce across water, avoiding torpedo nets and other underwater defenses, until it reached a dam, ship, or other destination, where it would sink and explode. By the end of the war, planes such as the allied forces' Avro Lancaster were delivering with 50 yd (46 m) accuracy from 20,000 ft (6,100 m), ten ton earthquake bombs (also invented by Barnes Wallis) named "Grand Slam", which, unusually for the time, were delivered from high altitude in order to gain high speed, and would, upon impact, penetrate and explode deep underground ("camouflet"), causing massive caverns or craters, and affecting targets too large or difficult to be affected by other types of bomb.

Modern military bomber aircraft are designed around a large-capacity internal bomb bay, while fighter-bombers usually carry bombs externally on pylons or bomb racks or on multiple ejection racks, which enable mounting several bombs on a single pylon. Some bombs are equipped with a parachute, such as the World War II "parafrag" (an 11 kg (24 lb) fragmentation bomb), the Vietnam War-era daisy cutters, and the bomblets of some modern cluster bombs. Parachutes slow the bomb's descent, giving the dropping aircraft time to get to a safe distance from the explosion. This is especially important with air-burst nuclear weapons (especially those dropped from slower aircraft or with very high yields), and in situations where the aircraft releases a bomb at low altitude. A number of modern bombs are also precision-guided munitions, and may be guided after they leave an aircraft by remote control, or by autonomous guidance.

Aircraft may also deliver bombs in the form of warheads on guided missiles, such as long-range cruise missiles, which can also be launched from warships.

A hand grenade is delivered by being thrown. Grenades can also be projected by other means, such as being launched from the muzzle of a rifle (as in the rifle grenade), using a grenade launcher (such as the M203), or by attaching a rocket to the explosive grenade (as in a rocket-propelled grenade (RPG)).

A bomb may also be positioned in advance and concealed.

A bomb destroying a rail track just before a train arrives will usually cause the train to derail. In addition to the damage to vehicles and people, a bomb exploding in a transport network often damages, and is sometimes mainly intended to damage, the network itself. This applies to railways, bridges, runways, and ports, and, to a lesser extent (depending on circumstances), to roads.

In the case of suicide bombing, the bomb is often carried by the attacker on their body, or in a vehicle driven to the target.

The Blue Peacock nuclear mines, which were also termed "bombs", were planned to be positioned during wartime and be constructed such that, if disturbed, they would explode within ten seconds.

The explosion of a bomb may be triggered by a detonator or a fuse. Detonators are triggered by clocks, remote controls like cell phones or some kind of sensor, such as pressure (altitude), radar, vibration or contact. Detonators vary in ways they work, they can be electrical, fire fuze or blast initiated detonators and others,

Blast seat

In forensic science, the point of detonation of a bomb is referred to as its blast seat, seat of explosion, blast hole or epicenter. Depending on the type, quantity and placement of explosives, the blast seat may be either spread out or concentrated (i.e., an explosion crater).

Other types of explosions, such as dust or vapor explosions, do not cause craters or even have definitive blast seats.

Blood vessel

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Blood_vessel

Blood vessel
Simple diagram of the human circulatory system

Blood vessels are the components of the circulatory system that transport blood throughout the human body. These vessels transport blood cells, nutrients, and oxygen to the tissues of the body. They also take waste and carbon dioxide away from the tissues. Blood vessels are needed to sustain life, because all of the body's tissues rely on their functionality.

There are five types of blood vessels: the arteries, which carry the blood away from the heart; the arterioles; the capillaries, where the exchange of water and chemicals between the blood and the tissues occurs; the venules; and the veins, which carry blood from the capillaries back towards the heart.

The word vascular, meaning relating to the blood vessels, is derived from the Latin vas, meaning vessel. Some structures – such as cartilage, the epithelium, and the lens and cornea of the eye – do not contain blood vessels and are labeled avascular.

Etymology

• artery: late Middle English; from Latin arteria, from Greek artēria, probably from airein ("raise")
• vein: Middle English; from Old French veine, from Latin vena. The earliest senses were "blood vessel" and "small natural underground channel of water".
• capillary: mid 17th century; from Latin capillaris, from capillus ("hair"), influenced by Old French capillaire.

Structure

The arteries and veins have three layers. The middle layer is thicker in the arteries than it is in the veins:

• The inner layer, tunica intima, is the thinnest layer. It is a single layer of flat cells (simple squamous epithelium) glued by a polysaccharide intercellular matrix, surrounded by a thin layer of subendothelial connective tissue interlaced with a number of circularly arranged elastic bands called the internal elastic lamina. A thin membrane of elastic fibers in the tunica intima run parallel to the vessel.
• The middle layer tunica media is the thickest layer in arteries. It consists of circularly arranged elastic fiber, connective tissue, polysaccharide substances, the second and third layer are separated by another thick elastic band called external elastic lamina. The tunica media may (especially in arteries) be rich in vascular smooth muscle, which controls the caliber of the vessel. Veins do not have the external elastic lamina, but only an internal one. The tunica media is thicker in the arteries rather than the veins.
• The outer layer is the tunica adventitia and the thickest layer in veins. It is entirely made of connective tissue. It also contains nerves that supply the vessel as well as nutrient capillaries (vasa vasorum) in the larger blood vessels.

Capillaries consist of a single layer of endothelial cells with a supporting subendothelium consisting of a basement membrane and connective tissue.

When blood vessels connect to form a region of diffuse vascular supply it is called an anastomosis. Anastomoses provide critical alternative routes for blood to flow in case of blockages.

Leg veins have valves which prevent backflow of the blood being pumped against gravity by the surrounding muscles.

Types

Transmission electron micrograph of a blood vessel displaying an erythrocyte (red blood cell, E) within its lumen, endothelial cells forming its tunica intima (inner layer), and pericytes forming its tunica adventitia (outer layer).

There are various kinds of blood vessels:

• Arteries
• Elastic arteries
• Distributing arteries
• Arterioles
• Capillaries (smallest blood vessels)
• Venules
• Veins
  • Large collecting vessels, such as the subclavian vein, the jugular vein, the renal vein and the iliac vein.
  • Venae cavae (the two largest veins, carry blood into the heart).
• Sinusoids
  • Extremely small vessels located within bone marrow, the spleen and the liver.

They are roughly grouped as "arterial" and "venous", determined by whether the blood in it is flowing away from (arterial) or toward (venous) the heart. The term "arterial blood" is nevertheless used to indicate blood high in oxygen, although the pulmonary artery carries "venous blood" and blood flowing in the pulmonary vein is rich in oxygen. This is because they are carrying the blood to and from the lungs, respectively, to be oxygenated.

Function

See also: Circulatory system

Blood vessels function to transport blood. In general, arteries and arterioles transport oxygenated blood from the lungs to the body and its organs, and veins and venules transport deoxygenated blood from the body to the lungs. Blood vessels also circulate blood throughout the circulatory system Oxygen (bound to hemoglobin in red blood cells) is the most critical nutrient carried by the blood. In all arteries apart from the pulmonary artery, hemoglobin is highly saturated (95–100%) with oxygen. In all veins apart from the pulmonary vein, the saturation of hemoglobin is about 75%. (The values are reversed in the pulmonary circulation.) In addition to carrying oxygen, blood also carries hormones, waste products and nutrients for cells of the body.

Blood vessels do not actively engage in the transport of blood (they have no appreciable peristalsis). Blood is propelled through arteries and arterioles through pressure generated by the heartbeat. Blood vessels also transport red blood cells which contain the oxygen necessary for daily activities. The amount of red blood cells present in your vessels has an effect on your health. Hematocrit tests can be performed to calculate the proportion of red blood cells in your blood. Higher proportions result in conditions such as dehydration or heart disease while lower proportions could lead to anemia and long-term blood loss.

Permeability of the endothelium is pivotal in the release of nutrients to the tissue. It is also increased in inflammation in response to histamine, prostaglandins and interleukins, which leads to most of the symptoms of inflammation (swelling, redness, warmth and pain).

Contraction

Constricted blood vessel.

Arteries—and veins to a degree—can regulate their inner diameter by contraction of the muscular layer. This changes the blood flow to downstream organs, and is determined by the autonomic nervous system. Vasodilation and vasoconstriction are also used antagonistically as methods of thermoregulation.

The size of blood vessels is different for each of them. It ranges from a diameter of about 25 millimeters for the aorta to only 8 micrometers in the capillaries. This comes out to about a 3000-fold range. Vasoconstriction is the constriction of blood vessels (narrowing, becoming smaller in cross-sectional area) by contracting the vascular smooth muscle in the vessel walls. It is regulated by vasoconstrictors (agents that cause vasoconstriction). These include paracrine factors (e.g. prostaglandins), a number of hormones (e.g. vasopressin and angiotensin) and neurotransmitters (e.g. epinephrine) from the nervous system.

Vasodilation is a similar process mediated by antagonistically acting mediators. The most prominent vasodilator is nitric oxide (termed endothelium-derived relaxing factor for this reason).

Flow

Main article: Vascular resistance

The circulatory system uses the channel of blood vessels to deliver blood to all parts of the body. This is a result of the left and right side of the heart working together to allow blood to flow continuously to the lungs and other parts of the body. Oxygen-poor blood enters the right side of the heart through two large veins. Oxygen-rich blood from the lungs enters through the pulmonary veins on the left side of the heart into the aorta and then reaches the rest of the body. The capillaries are responsible for allowing the blood to receive oxygen through tiny air sacs in the lungs. This is also the site where carbon dioxide exits the blood. This all occurs in the lungs where blood is oxygenated.

The blood pressure in blood vessels is traditionally expressed in millimetres of mercury (1 mmHg = 133 Pa). In the arterial system, this is usually around 120 mmHg systolic (high pressure wave due to contraction of the heart) and 80 mmHg diastolic (low pressure wave). In contrast, pressures in the venous system are constant and rarely exceed 10 mmHg.

Vascular resistance occurs where the vessels away from the heart oppose the flow of blood. Resistance is an accumulation of three different factors: blood viscosity, blood vessel length, and vessel radius.

Blood viscosity is the thickness of the blood and its resistance to flow as a result of the different components of the blood. Blood is 92% water by weight and the rest of blood is composed of protein, nutrients, electrolytes, wastes, and dissolved gases. Depending on the health of an individual, the blood viscosity can vary (i.e. anemia causing relatively lower concentrations of protein, high blood pressure an increase in dissolved salts or lipids, etc.).

Vessel length is the total length of the vessel measured as the distance away from the heart. As the total length of the vessel increases, the total resistance as a result of friction will increase.

Vessel radius also affects the total resistance as a result of contact with the vessel wall. As the radius of the wall gets smaller, the proportion of the blood making contact with the wall will increase. The greater amount of contact with the wall will increase the total resistance against the blood flow.

Disease

Main article: Vascular disease

Blood vessels play a huge role in virtually every medical condition. Cancer, for example, cannot progress unless the tumor causes angiogenesis (formation of new blood vessels) to supply the malignant cells' metabolic demand. Atherosclerosis, the narrowing of the blood vessels due to the buildup of plaque, and the coronary artery disease that often follows can cause heart attacks or cardiac arrest and is the leading cause of death worldwide resulting in 8.9 million deaths or 16% of all deaths.

Blood vessel permeability is increased in inflammation. Damage, due to trauma or spontaneously, may lead to hemorrhage due to mechanical damage to the vessel endothelium. In contrast, occlusion of the blood vessel by atherosclerotic plaque, by an embolised blood clot or a foreign body leads to downstream ischemia (insufficient blood supply) and possibly infarction (necrosis due to lack of blood supply). Vessel occlusion tends to be a positive feedback system; an occluded vessel creates eddies in the normally laminar flow or plug flow blood currents. These eddies create abnormal fluid velocity gradients which push blood elements such as cholesterol or chylomicron bodies to the endothelium. These deposit onto the arterial walls which are already partially occluded and build upon the blockage.

The most common disease of the blood vessels is hypertension or high blood pressure. This is caused by an increase in the pressure of the blood flowing through the vessels. Hypertension can lead to more serious conditions such as heart failure and stroke. To prevent these diseases, the most common treatment option is medication as opposed to surgery. Aspirin helps prevent blood clots and can also help limit inflammation.

Vasculitis is inflammation of the vessel wall, due to autoimmune disease or infection.

Another Blood Vessel Disease is called Broken Blood Vessel. Broken blood vessels, also known as spider veins or telangiectasias, are small, damaged blood vessels that appear as red, purple, or blue lines on the skin's surface. They are most commonly found on the face, legs, and chest. These unsightly blemishes can be caused by various factors, and their appearance may cause concerns about both aesthetics and potential health issues.

Quadratic formula

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quadratic_formula

The quadratic function y = 1/2x² − 5/2x + 2, with roots x = 1 and x = 4.

In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, grouping, AC method), completing the square, graphing and others.

Given a general quadratic equation of the form

$${\displaystyle a{x}^2+bx+c=0}$$

whose discriminant ${\displaystyle b^2-4ac}$ is positive, with x representing an unknown, with a, b and c representing constants, and with a ≠ 0, the quadratic formula is:

$${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}$$

where the plus–minus symbol "±" indicates that the quadratic equation has two solutions. Written separately, they become:

$${\displaystyle \begin{array}{rl}{x}_1& =\frac{-b+\sqrt{b^2-4ac}}{2a}\text{and}\\ x_2& =\frac{-b-\sqrt{b^2-4ac}}{2a}\end{array}}$$

Each of these two solutions is also called a root (or zero) of the quadratic equation. Geometrically, these roots represent the x-values at which any parabola, explicitly given as y = ax² + bx + c, crosses the x-axis.

As well as being a formula that yields the zeros of any parabola, the quadratic formula can also be used to identify the axis of symmetry of the parabola, and the number of real zeros the quadratic equation contains.

The expression b² − 4ac is known as the discriminant. If a, b, and c are real numbers and a ≠ 0 then

1. When b² − 4ac > 0, there are two distinct real roots or solutions to the equation ax² + bx + c = 0.
2. When b² − 4ac = 0, there is one repeated real solution.
3. When b² − 4ac < 0, there are two distinct complex solutions, which are complex conjugates of each other.

Equivalent formulations

The quadratic formula, in the case when the discriminant ${\displaystyle b^2-4ac}$ is positive, may also be written as

$${\displaystyle x=-\frac{b}{2a}\pm \sqrt{\frac{b^2-4ac}{4a^2}},}$$

which may be simplified to

$${\displaystyle x=-\frac{b}{2a}\pm \sqrt{{\left(\frac{b}{2a}\right)}^2-\frac{c}{a}}.}$$

This version of the formula makes it easy to find the roots when using a calculator.

When b is an even integer, it is usually easier to use the reduced formula

$${\displaystyle x=\frac{-\frac{b}{2}\pm \sqrt{{\left(\frac{b}{2}\right)}^2-ac}}{a}}$$

In the case when the discriminant ${\displaystyle b^2-4ac}$ is negative, complex roots are involved. The quadratic formula can be written as:

$${\displaystyle x=-\frac{b}{2a}\pm i\sqrt{\left|{\left(\frac{b}{2a}\right)}^2-\frac{c}{a}\right|}.}$$

Muller's method

A lesser known quadratic formula, also named "citardauq", which is used in Muller's method and which can be found from Vieta's formulas, provides (assuming a ≠ 0, c ≠ 0) the same roots via the equation:

$${\displaystyle x=\frac{-2c}{b\pm \sqrt{b^2-4ac}}=\frac{2c}{-b\mp \sqrt{b^2-4ac}}.}$$

For positive ${\displaystyle b}$, the subtraction causes cancellation in the standard formula (respectively negative ${\displaystyle b}$ and addition), resulting in poor accuracy. In this case, switching to Muller's formula with the opposite sign is a good workaround.

Formulations based on alternative parameterizations

The standard parameterization of the quadratic equation is

$${\displaystyle a{x}^2+bx+c=0.}$$

Some sources, particularly older ones, use alternative parameterizations of the quadratic equation such as

$${\displaystyle a{x}^2-2b_{1}x+c=0,}$$

where ${\displaystyle b_1=-b/2}$,

or

$${\displaystyle a{x}^2+2b_{2}x+c=0,}$$

where ${\displaystyle b_2=b/2}$.

These alternative parameterizations result in slightly different forms for the solution, but they are otherwise equivalent to the standard parameterization.

Derivations of the formula

Many different methods to derive the quadratic formula are available in the literature. The standard one is a simple application of the completing the square technique. Alternative methods are sometimes simpler than completing the square, and may offer interesting insight into other areas of mathematics.

By completing the square

Divide the quadratic equation by ${\displaystyle a}$, which is allowed because ${\displaystyle a}$ is non-zero:

$${\displaystyle x^2+\frac{b}{a}x+\frac{c}{a}=0.}$$

Subtract c/a from both sides of the equation, yielding:

$${\displaystyle x^2+\frac{b}{a}x=-\frac{c}{a}.}$$

The quadratic equation is now in a form to which the method of completing the square is applicable. In fact, by adding a constant to both sides of the equation such that the left hand side becomes a complete square, the quadratic equation becomes:

$${\displaystyle x^2+\frac{b}{a}x+{\left(\frac{b}{2a}\right)}^2=-\frac{c}{a}+{\left(\frac{b}{2a}\right)}^2,}$$

which produces:

$${\displaystyle {\left(x+\frac{b}{2a}\right)}^2=-\frac{c}{a}+\frac{b^2}{4a^2}.}$$

Accordingly, after rearranging the terms on the right hand side to have a common denominator, we obtain:

$${\displaystyle {\left(x+\frac{b}{2a}\right)}^2=\frac{b^2-4ac}{4a^2}.}$$

The square has thus been completed. If the discriminant ${\displaystyle b^2-4ac}$ is positive, we can take the square root of both sides, yielding the following equation:

$${\displaystyle x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}.}$$

(In fact, this equation remains true even if the discriminant is not positive, by interpreting the root of the discriminant as any of its two opposite complex roots.)

In which case, isolating the ${\displaystyle x}$ would give the quadratic formula:

$${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.}$$

There are many alternatives of this derivation with minor differences, mostly concerning the manipulation of ${\displaystyle a}$.

Shorter method

Completing the square can also be accomplished by a sometimes shorter and simpler sequence:^[11]

1. Multiply each side by ${\displaystyle 4a}$,
2. Rearrange.
3. Add ${\displaystyle b^2}$ to both sides to complete the square.
4. The left side is the outcome of the polynomial ${\displaystyle (2ax+b{)}^2}$.
5. Take the square root of both sides.
6. Isolate ${\displaystyle x}$.

In which case, the quadratic formula can also be derived as follows:

$${\displaystyle \begin{array}{llllllc}a{x}^2& +& bx& +& c& =& 0\\ 4a^2{x}^2& +& 4abx& +& 4ac& =& 0\\ 4a^2{x}^2& +& 4abx& & & =& -4ac\\ 4a^2{x}^2& +& 4abx& +& b^2& =& b^2-4ac\\ & & (2ax+b{)}^2& & & =& b^2-4ac\\ \text{ (valid if }{b}^2-4ac\text{ is positive)}& & 2ax+b& & & =& \pm \sqrt{b^2-4ac}\\ & & 2ax& & & =& -b\pm \sqrt{b^2-4ac}\\ & & & & x& =& {\displaystyle \frac{-b\pm \sqrt{b^2-4ac}}{2a}}.\\ \end{array}}$$

This derivation of the quadratic formula is ancient and was known in India at least as far back as 1025. Compared with the derivation in standard usage, this alternate derivation avoids fractions and squared fractions until the last step and hence does not require a rearrangement after step 3 to obtain a common denominator in the right side.

By substitution

Another technique is solution by substitution. In this technique, we substitute ${\displaystyle x=y+m}$ into the quadratic to get:

$${\displaystyle a(y+m{)}^2+b(y+m)+c=0.}$$

Expanding the result and then collecting the powers of ${\displaystyle y}$ produces:

$${\displaystyle a{y}^2+y(2am+b)+\left(a{m}^2+bm+c\right)=0.}$$

We have not yet imposed a second condition on ${\displaystyle y}$ and ${\displaystyle m}$, so we now choose ${\displaystyle m}$ so that the middle term vanishes. That is, ${\displaystyle 2am+b=0}$ or ${\displaystyle m=\frac{-b}{2a}}$.

$${\displaystyle a{y}^2+y(0)+\left(a{m}^2+bm+c\right)=0.}$$

$${\displaystyle a{y}^2+\left(a{m}^2+bm+c\right)=0.}$$

Subtracting the constant term from both sides of the equation (to move it to the right hand side) and then dividing by ${\displaystyle a}$ gives:

$${\displaystyle y^2=\frac{-\left(a{m}^2+bm+c\right)}{a}.}$$

Substituting for ${\displaystyle m}$ gives:

$${\displaystyle y^2=\frac{-\left(\frac{b^2}{4a}+\frac{-b^2}{2a}+c\right)}{a}=\frac{b^2-4ac}{4a^2}.}$$

Therefore,

$${\displaystyle y=\pm \frac{\sqrt{b^2-4ac}}{2a}}$$

By re-expressing ${\displaystyle y}$ in terms of ${\displaystyle x}$ using the formula $x=y+m=y-\frac{b}{2a}$ , the usual quadratic formula can then be obtained:

$${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.}$$

By using algebraic identities

The following method was used by many historical mathematicians:

Let the roots of the standard quadratic equation be r₁ and r₂. The derivation starts by recalling the identity:

$${\displaystyle (r_1-r_2{)}^2=(r_1+r_2{)}^2-4r_1{r}_2.}$$

Taking the square root on both sides, we get:

$${\displaystyle r_1-r_2=\pm \sqrt{(r_1+r_2{)}^2-4r_1{r}_2}.}$$

Since the coefficient a ≠ 0, we can divide the standard equation by a to obtain a quadratic polynomial having the same roots. Namely,

$${\displaystyle x^2+\frac{b}{a}x+\frac{c}{a}=(x-r_1)(x-r_2)=x^2-(r_1+r_2)x+r_1{r}_2.}$$

From this we can see that the sum of the roots of the standard quadratic equation is given by −b/a, and the product of those roots is given by c/a. Hence the identity can be rewritten as:

$${\displaystyle r_1-r_2=\pm \sqrt{{\left(-\frac{b}{a}\right)}^2-4\frac{c}{a}}=\pm \sqrt{\frac{b^2}{a^2}-\frac{4ac}{a^2}}=\pm \frac{\sqrt{b^2-4ac}}{a}.}$$

Now,

$${\displaystyle r_1=\frac{(r_1+r_2)+(r_1-r_2)}{2}=\frac{-\frac{b}{a}\pm \frac{\sqrt{b^2-4ac}}{a}}{2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.}$$

Since r₂ = −r₁ − b/a, if we take

$${\displaystyle r_1=\frac{-b+\sqrt{b^2-4ac}}{2a}}$$

then we obtain

$${\displaystyle r_2=\frac{-b-\sqrt{b^2-4ac}}{2a};}$$

and if we instead take

$${\displaystyle r_1=\frac{-b-\sqrt{b^2-4ac}}{2a}}$$

then we calculate that

$${\displaystyle r_2=\frac{-b+\sqrt{b^2-4ac}}{2a}.}$$

Combining these results by using the standard shorthand ±, we have that the solutions of the quadratic equation are given by:

$${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.}$$

By Lagrange resolvents

Further information: Lagrange resolvents

An alternative way of deriving the quadratic formula is via the method of Lagrange resolvents, which is an early part of Galois theory. This method can be generalized to give the roots of cubic polynomials and quartic polynomials, and leads to Galois theory, which allows one to understand the solution of algebraic equations of any degree in terms of the symmetry group of their roots, the Galois group.

This approach focuses on the roots more than on rearranging the original equation. Given a monic quadratic polynomial

$${\displaystyle x^2+px+q,}$$

assume that it factors as

$${\displaystyle x^2+px+q=(x-\alpha )(x-\beta ),}$$

Expanding yields

$${\displaystyle x^2+px+q=x^2-(\alpha +\beta )x+\alpha \beta ,}$$

where p = −(α + β) and q = αβ.

Since the order of multiplication does not matter, one can switch α and β and the values of p and q will not change: one can say that p and q are symmetric polynomials in α and β. In fact, they are the elementary symmetric polynomials – any symmetric polynomial in α and β can be expressed in terms of α + β and αβ. The Galois theory approach to analyzing and solving polynomials is: given the coefficients of a polynomial, which are symmetric functions in the roots, can one "break the symmetry" and recover the roots? Thus solving a polynomial of degree n is related to the ways of rearranging ("permuting") n terms, which is called the symmetric group on n letters, and denoted S_n. For the quadratic polynomial, the only ways to rearrange two terms is to leave them be or to swap them ("transpose" them), and thus solving a quadratic polynomial is simple.

To find the roots α and β, consider their sum and difference:

$${\displaystyle \begin{array}{rl}{r}_1& =\alpha +\beta \\ r_2& =\alpha -\beta .\end{array}}$$

These are called the Lagrange resolvents of the polynomial; notice that one of these depends on the order of the roots, which is the key point. One can recover the roots from the resolvents by inverting the above equations:

$${\displaystyle \begin{array}{rl}\alpha & =\frac{1}{2}\left(r_1+r_2\right)\\ \beta & =\frac{1}{2}\left(r_1-r_2\right).\end{array}}$$

Thus, solving for the resolvents gives the original roots.

Now r₁ = α + β is a symmetric function in α and β, so it can be expressed in terms of p and q, and in fact r₁ = −p as noted above. But r₂ = α − β is not symmetric, since switching α and β yields −r₂ = β − α (formally, this is termed a group action of the symmetric group of the roots). Since r₂ is not symmetric, it cannot be expressed in terms of the coefficients p and q, as these are symmetric in the roots and thus so is any polynomial expression involving them. Changing the order of the roots only changes r₂ by a factor of −1, and thus the square r₂² = (α − β)² is symmetric in the roots, and thus expressible in terms of p and q. Using the equation

$${\displaystyle (\alpha -\beta {)}^2=(\alpha +\beta {)}^2-4\alpha \beta }$$

yields

$${\displaystyle r_2^2=p^2-4q}$$

and thus

$${\displaystyle r_2=\pm \sqrt{p^2-4q}}$$

If one takes the positive root, breaking symmetry, one obtains:

$${\displaystyle \begin{array}{rl}{r}_1& =-p\\ r_2& =\sqrt{p^2-4q}\end{array}}$$

and thus

$${\displaystyle \begin{array}{rl}\alpha & =\frac{1}{2}\left(-p+\sqrt{p^2-4q}\right)\\ \beta & =\frac{1}{2}\left(-p-\sqrt{p^2-4q}\right).\end{array}}$$

Thus the roots are

$${\displaystyle \frac{1}{2}\left(-p\pm \sqrt{p^2-4q}\right)}$$

which is the quadratic formula. Substituting p = b/a, q = c/a yields the usual form for when a quadratic is not monic. The resolvents can be recognized as r₁/2 = −p/2 = −b/2a being the vertex, and r₂² = p² − 4q is the discriminant (of a monic polynomial).

A similar but more complicated method works for cubic equations, where one has three resolvents and a quadratic equation (the "resolving polynomial") relating r₂ and r₃, which one can solve by the quadratic equation, and similarly for a quartic equation (degree 4), whose resolving polynomial is a cubic, which can in turn be solved. The same method for a quintic equation yields a polynomial of degree 24, which does not simplify the problem, and, in fact, solutions to quintic equations in general cannot be expressed using only roots.

Historical development

The earliest methods for solving quadratic equations were geometric. Babylonian cuneiform tablets contain problems reducible to solving quadratic equations. The Egyptian Berlin Papyrus, dating back to the Middle Kingdom (2050 BC to 1650 BC), contains the solution to a two-term quadratic equation.

The Greek mathematician Euclid (circa 300 BC) used geometric methods to solve quadratic equations in Book 2 of his Elements, an influential mathematical treatise. Rules for quadratic equations appear in the Chinese The Nine Chapters on the Mathematical Art circa 200 BC. In his work Arithmetica, the Greek mathematician Diophantus (circa 250 AD) solved quadratic equations with a method more recognizably algebraic than the geometric algebra of Euclid. His solution gives only one root, even when both roots are positive.

The Indian mathematician Brahmagupta (597–668 AD) explicitly described the quadratic formula in his treatise Brāhmasphuṭasiddhānta published in 628 AD, but written in words instead of symbols. His solution of the quadratic equation ax² + bx = c was as follows: "To the absolute number multiplied by four times the [coefficient of the] square, add the square of the [coefficient of the] middle term; the square root of the same, less the [coefficient of the] middle term, being divided by twice the [coefficient of the] square is the value." This is equivalent to:

$${\displaystyle x=\frac{\sqrt{c\cdot 4a+b^2}-b}{2a}.}$$

Śrīdharācāryya (870–930 AD), an Indian mathematician also came up with a similar algorithm for solving quadratic equations, though there is no indication that he considered both the roots. The 9th-century Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī solved quadratic equations algebraically. The quadratic formula covering all cases was first obtained by Simon Stevin in 1594. In 1637 René Descartes published La Géométrie containing special cases of the quadratic formula in the form we know today.

Significant uses

Geometric significance

Graph of y = ax² + bx + c, where a and the discriminant b² − 4ac are positive, with

• Roots and y-intercept in red
• Vertex and axis of symmetry in blue
• Focus and directrix in pink

In terms of coordinate geometry, a parabola is a curve whose (x, y)-coordinates are described by a second-degree polynomial, i.e. any equation of the form:

$${\displaystyle y=p(x)=a_2{x}^2+a_{1}x+a_0,}$$

where p represents the polynomial of degree 2 and a₀, a₁, and a₂ ≠ 0 are constant coefficients whose subscripts correspond to their respective term's degree. The geometrical interpretation of the quadratic formula is that it defines the points on the x-axis where the parabola will cross the axis. Additionally, if the quadratic formula was looked at as two terms,

$${\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}=-\frac{b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}}$$

the axis of symmetry appears as the line x = −b/2a. The other term, √b² − 4ac/2a, gives the distance the zeros are away from the axis of symmetry, where the plus sign represents the distance to the right, and the minus sign represents the distance to the left.

If this distance term were to decrease to zero, the value of the axis of symmetry would be the x value of the only zero, that is, there is only one possible solution to the quadratic equation. Algebraically, this means that √b² − 4ac = 0, or simply b² − 4ac = 0 (where the left-hand side is referred to as the discriminant). This is one of three cases, where the discriminant indicates how many zeros the parabola will have. If the discriminant is positive, the distance would be non-zero, and there will be two solutions. However, there is also the case where the discriminant is less than zero, and this indicates the distance will be imaginary – or some multiple of the complex unit i, where i = √−1 – and the parabola's zeros will be complex numbers. The complex roots will be complex conjugates, where the real part of the complex roots will be the value of the axis of symmetry. There will be no real values of x where the parabola crosses the x-axis.

Dimensional analysis

If the constants a, b, and/or c are not unitless then the units of x must be equal to the units of b/a, due to the requirement that ax² and bx agree on their units. Furthermore, by the same logic, the units of c must be equal to the units of b²/a, which can be verified without solving for x. This can be a powerful tool for verifying that a quadratic expression of physical quantities has been set up correctly.