In quantum field theory, force carriers or messenger particles or intermediate particles are particles that give rise to forces between other particles. These particles are bundles of energy (quanta) of a particular kind of field. There is one kind of field for every type of elementary particle. For instance, there is an electromagnetic field whose quanta are photons. The concept is especially important in particle physics where the force carrier particles that mediate the electromagnetic, weak, and strong interactions are called gauge bosons.
Particle and field viewpoints
Quantum field theories describe nature in terms of fields. Each field has a complementary description as the set of particles of a particular type. A force between two particles can be described either as the action of a force field generated by one particle on the other, or in terms of the exchange of virtual force carrier particles between them.
The energy of a wave in a field (for example, electromagnetic waves in the electromagnetic field) is quantized, and the quantum excitations of the field can be interpreted as particles. The Standard Model contains the following particles, each of which is an excitation of a particular field:
- Gluons, excitations of the strong gauge field.
- Photons, W bosons, and Z bosons, excitations of the electroweak gauge fields.
- Higgs bosons, excitations of one component of the Higgs field, which gives mass to fundamental particles.
In addition, composite particles such as mesons, as well as quasiparticles, can be described as excitations of an effective field.
Gravity is not a part of the Standard Model, but it is thought that there may be particles called gravitons which are the excitations of gravitational waves. The status of this particle is still tentative, because the theory is incomplete and because the interactions of single gravitons may be too weak to be detected.
Forces from the particle viewpoint
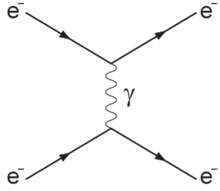
When one particle scatters off another, altering its trajectory, there are two ways to think about the process. In the field picture, we imagine that the field generated by one particle caused a force on the other. Alternatively, we can imagine one particle emitting a virtual particle which is absorbed by the other. The virtual particle transfers momentum from one particle to the other. This particle viewpoint is especially helpful when there are a large number of complicated quantum corrections to the calculation since these corrections can be visualized as Feynman diagrams containing additional virtual particles.
Another example involving virtual particles is beta decay where a virtual W boson is emitted by a nucleon and then decays to e± and (anti)neutrino.
The description of forces in terms of virtual particles is limited by the applicability of the perturbation theory from which it is derived. In certain situations, such as low-energy QCD and the description of bound states, perturbation theory breaks down.
History
The concept of messenger particles dates back to the 18th century when the French physicist Charles Coulomb showed that the electrostatic force between electrically charged objects follows a law similar to Newton's Law of Gravitation. In time, this relationship became known as Coulomb's law. By 1862, Hermann von Helmholtz had described a ray of light as the "quickest of all the messengers". In 1905, Albert Einstein proposed the existence of a light-particle in answer to the question: "what are light quanta?"
In 1923, at the Washington University in St. Louis, Arthur Holly Compton demonstrated an effect now known as Compton scattering. This effect is only explainable if light can behave as a stream of particles and it convinced the physics community of the existence of Einstein's light-particle. Lastly, in 1926, one year before the theory of quantum mechanics was published, Gilbert N. Lewis introduced the term "photon", which soon became the name for Einstein's light particle. From there, the concept of messenger particles developed further, notably to massive force carriers (e.g. for the Yukawa potential).