https://en.wikipedia.org/wiki/Bucket_argument
Isaac Newton's rotating bucket argument (also known as Newton's bucket) was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies. It is one of five arguments from the "properties, causes, and effects" of "true motion and rest" that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?" General relativity dispenses with absolute space and with physics whose cause is external to the system, with the concept of geodesics of spacetime.
Isaac Newton's rotating bucket argument (also known as Newton's bucket) was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies. It is one of five arguments from the "properties, causes, and effects" of "true motion and rest" that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition of what is meant by "absolute rotation", and do not pretend to address the question of "rotation relative to what?" General relativity dispenses with absolute space and with physics whose cause is external to the system, with the concept of geodesics of spacetime.
Background
These arguments, and a discussion of the distinctions between absolute and relative time, space, place and motion, appear in a General Scholium at the very beginning of Newton's work, The Mathematical Principles of Natural Philosophy (1687), which established the foundations of classical mechanics and introduced his law of universal gravitation, which yielded the first quantitatively adequate dynamical explanation of planetary motion.
Despite their embrace of the principle of rectilinear inertia and the recognition of the kinematical relativity of apparent motion (which underlies whether the Ptolemaic or the Copernican
system is correct), natural philosophers of the seventeenth century
continued to consider true motion and rest as physically separate
descriptors of an individual body. The dominant view Newton opposed was
devised by René Descartes, and was supported (in part) by Gottfried Leibniz.
It held that empty space is a metaphysical impossibility because space
is nothing other than the extension of matter, or, in other words, that
when one speaks of the space between things one is actually making
reference to the relationship that exists between those things and not
to some entity that stands between them.
Concordant with the above understanding, any assertion about the
motion of a body boils down to a description over time in which the body
under consideration is at t1 found in the vicinity of one group of "landmark" bodies and at some t2 is found in the vicinity of some other "landmark" body or bodies.
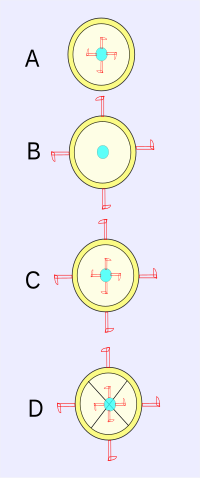
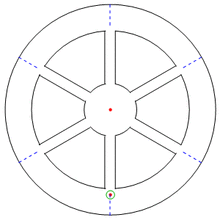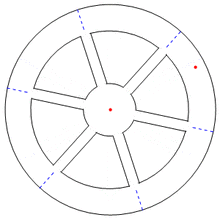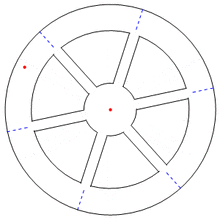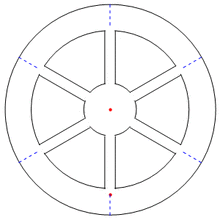
Detection
of rotation: red flags pop out on flexible arms when either object
actually rotates. A: Central object rotates. B: Outer ring rotates, but
in opposite direction. C: Both rotate, but in opposite directions. D:
Both are locked together and rotate in the same direction.
Descartes recognized that there would be a real difference, however,
between a situation in which a body with movable parts and originally at
rest with respect to a surrounding ring was itself accelerated to a
certain angular velocity with respect to the ring, and another situation
in which the surrounding ring were given a contrary acceleration with
respect to the central object. With sole regard to the central object
and the surrounding ring, the motions would be indistinguishable from
each other assuming that both the central object and the surrounding
ring were absolutely rigid objects. However, if neither the central
object nor the surrounding ring were absolutely rigid then the parts of
one or both of them would tend to fly out from the axis of rotation.
For contingent reasons having to do with the Inquisition, Descartes spoke of motion as both absolute and relative.
However, his real position was that motion is absolute.
By the late 19th century, the contention that all motion is relative was re-introduced, notably by Ernst Mach (1883).
When, accordingly, we say that a body preserves unchanged its direction and velocity in space, our assertion is nothing more or less than an abbreviated reference to the entire universe.
The argument
Newton discusses a bucket (Latin: situla) filled with water hung by a cord.
If the cord is twisted up tightly on itself and then the bucket is
released, it begins to spin rapidly, not only with respect to the
experimenter, but also in relation to the water it contains. (This
situation would correspond to diagram B above.)
Although the relative motion at this stage is the greatest, the
surface of the water remains flat, indicating that the parts of the
water have no tendency to recede from the axis of relative motion,
despite proximity to the pail. Eventually, as the cord continues to
unwind, the surface of the water assumes a concave shape as it acquires
the motion of the bucket spinning relative to the experimenter. This
concave shape shows that the water is rotating, despite the fact that
the water is at rest relative to the pail. In other words, it is not the
relative motion of the pail and water that causes concavity of the
water, contrary to the idea that motions can only be relative, and that
there is no absolute motion. (This situation would correspond to diagram
D.) Possibly the concavity of the water shows rotation relative to something else: say absolute space? Newton says: "One can find out and measure the true and absolute circular motion of the water".
In the 1846 Andrew Motte translation of Newton's words:
If a vessel, hung by a long cord, is so often turned about that the cord is strongly twisted, then filled with water, and held at rest together with the water; after, by the sudden action of another force, it is whirled about in the contrary way, and while the cord is untwisting itself, the vessel continues for some time this motion; the surface of the water will at first be plain, as before the vessel began to move; but the vessel by gradually communicating its motion to the water, will make it begin sensibly to revolve, and recede by little and little, and ascend to the sides of the vessel, forming itself into a concave figure...This ascent of the water shows its endeavour to recede from the axis of its motion; and the true and absolute circular motion of the water, which is here directly contrary to the relative, discovers itself, and may be measured by this endeavour. ... And therefore, this endeavour does not depend upon any translation of the water in respect to ambient bodies, nor can true circular motion be defined by such translation. ...; but relative motions...are altogether destitute of any real effect. ...It is indeed a matter of great difficulty to discover, and effectually to distinguish, the true motions of particular bodies from the apparent; because the parts of that immovable space in which these motions are performed, do by no means come under the observations of our senses.
— Isaac Newton; Principia, Book 1: Scholium
The argument that the motion is absolute, not relative, is
incomplete, as it limits the participants relevant to the experiment to
only the pail and the water, a limitation that has not been established.
In fact, the concavity of the water clearly involves gravitational
attraction, and by implication the Earth also is a participant. Here is a
critique due to Mach arguing that only relative motion is established:
Newton's experiment with the rotating vessel of water simply informs us that the relative rotation of the water with respect to the sides of the vessel produces no noticeable centrifugal forces, but that such forces are produced by its relative rotations with respect to the mass of the earth and other celestial bodies.
— Ernst Mach, as quoted by L. Bouquiaux in Leibniz, p. 104
The degree in which Mach's hypothesis is integrated in general relativity is discussed in the article Mach's principle; it is generally held that general relativity is not entirely Machian.
All observers agree that the surface of rotating water is curved.
However, the explanation of this curvature involves centrifugal force
for all observers with the exception of a truly stationary observer, who
finds the curvature is consistent with the rate of rotation of the
water as they observe it, with no need for an additional centrifugal
force. Thus, a stationary frame can be identified, and it is not
necessary to ask "Stationary with respect to what?":
The original question, "relative to what frame of reference do the laws of motion hold?" is revealed to be wrongly posed. For the laws of motion essentially determine a class of reference frames, and (in principle) a procedure for constructing them.
A supplementary thought experiment
with the same objective of determining the occurrence of absolute
rotation also was proposed by Newton: the example of observing two
identical spheres in rotation about their center of gravity and tied
together by a string. Occurrence of tension in the string is indicative
of absolute rotation; see Rotating spheres.
Detailed analysis
The interface of two immiscible liquids rotating around a vertical axis is an upward-opening circular paraboloid.
The historic interest of the rotating bucket experiment is its
usefulness in suggesting one can detect absolute rotation by observation
of the shape of the surface of the water. However, one might question
just how rotation brings about this change. Below are two approaches to
understanding the concavity of the surface of rotating water in a
bucket.
Force diagram for an element of water surface in co-rotating frame. Top:
Radial section and selected point on water surface; the water, the
co-rotating frame, and the radial section share a constant angular rate
of rotation given by the vector Ω. Bottom: Force diagram at selected point on surface. The slope of the surface adjusts to make all three forces sum to zero.
Newton's laws of motion
The shape of the surface of a rotating liquid in a bucket can be
determined using Newton's laws for the various forces on an element of
the surface. For example, see Knudsen and Hjorth.
The analysis begins with the free body diagram in the co-rotating frame
where the water appears stationary. The height of the water h = h(r) is a function of the radial distance r from the axis of rotation Ω,
and the aim is to determine this function. An element of water volume
on the surface is shown to be subject to three forces: the vertical
force due to gravity Fg, the horizontal, radially outward centrifugal force FCfgl, and the force normal to the surface of the water Fn
due to the rest of the water surrounding the selected element of
surface. The force due to surrounding water is known to be normal to the
surface of the water because a liquid in equilibrium cannot support shear stresses. To quote Anthony and Brackett:
The surface of a fluid of uniform density..., if at rest, is everywhere perpendicular to the lines of force; for if this were not so, the force at a point on the surface could be resolved into two components, one perpendicular and the other tangent to the surface. But from the nature of a fluid, the tangential force would set up a motion of the fluid, which is contrary to the statement that the fluid is at rest.
— William Arnold Anthony & Cyrus Fogg Brackett: Elementary Text-book of Physics, p. 127
Moreover, because the element of water does not move,
the sum of all three forces must be zero. To sum to zero, the force of
the water must point oppositely to the sum of the centrifugal and
gravity forces, which means the surface of the water must adjust so its
normal points in this direction. (A very similar problem is the design
of a banked turn,
where the slope of the turn is set so a car will not slide off the
road. The analogy in the case of rotating bucket is that the element of
water surface will "slide" up or down the surface unless the normal to
the surface aligns with the vector resultant formed by the vector addition Fg + FCfgl.)
As r increases, the centrifugal force increases according to the relation (the equations are written per unit mass):
where Ω is the constant rate of rotation of the water. The gravitational force is unchanged at
where g is the acceleration due to gravity. These two forces add to make a resultant at an angle φ from the vertical given by
which clearly becomes larger as r increases. To ensure that
this resultant is normal to the surface of the water, and therefore can
be effectively nulled by the force of the water beneath, the normal to
the surface must have the same angle, that is,
leading to the ordinary differential equation for the shape of the surface:
or, integrating:
where h(0) is the height of the water at r = 0. In words, the surface of the water is parabolic in its dependence upon the radius.
Potential energy
The shape of the water's surface can be found in a different, very intuitive way using the interesting idea of the potential energy associated with the centrifugal force in the co-rotating frame.
In a reference frame uniformly rotating at angular rate Ω, the fictitious centrifugal force is conservative and has a potential energy of the form:
where r is the radius from the axis of rotation. This result
can be verified by taking the gradient of the potential to obtain the
radially outward force:
The meaning of the potential energy is that movement of a test body from a larger radius to a smaller radius involves doing work against the centrifugal force.
The potential energy is useful, for example, in understanding the
concavity of the water surface in a rotating bucket. Notice that at equilibrium
the surface adopts a shape such that an element of volume at any
location on its surface has the same potential energy as at any other.
That being so, no element of water on the surface has any incentive to
move position, because all positions are equivalent in energy. That is,
equilibrium is attained. On the other hand, were surface regions with
lower energy available, the water occupying surface locations of higher
potential energy would move to occupy these positions of lower energy,
inasmuch as there is no barrier to lateral movement in an ideal liquid.
We might imagine deliberately upsetting this equilibrium
situation by somehow momentarily altering the surface shape of the water
to make it different from an equal-energy surface. This change in shape
would not be stable, and the water would not stay in our artificially
contrived shape, but engage in a transient exploration of many shapes
until non-ideal frictional forces introduced by sloshing, either against
the sides of the bucket or by the non-ideal nature of the liquid,
killed the oscillations and the water settled down to the equilibrium
shape.
To see the principle of an equal-energy surface at work, imagine
gradually increasing the rate of rotation of the bucket from zero. The
water surface is flat at first, and clearly a surface of equal potential
energy because all points on the surface are at the same height in the
gravitational field acting upon the water. At some small angular rate of
rotation, however, an element of surface water can achieve lower
potential energy by moving outward under the influence of the
centrifugal force. Because water is incompressible and must remain
within the confines of the bucket, this outward movement increases the
depth of water at the larger radius, increasing the height of the
surface at larger radius, and lowering it at smaller radius. The surface
of the water becomes slightly concave, with the consequence that the
potential energy of the water at the greater radius is increased by the
work done against gravity to achieve the greater height. As the height
of water increases, movement toward the periphery becomes no longer
advantageous, because the reduction in potential energy from working
with the centrifugal force is balanced against the increase in energy
working against gravity. Thus, at a given angular rate of rotation, a
concave surface represents the stable situation, and the more rapid the
rotation, the more concave this surface. If rotation is arrested, the
energy stored in fashioning the concave surface must be dissipated, for
example through friction, before an equilibrium flat surface is
restored.
To implement a surface of constant potential energy quantitatively, let the height of the water be : then the potential energy per unit mass contributed by gravity is and the total potential energy per unit mass on the surface is
with the background energy level independent of r. In a static situation (no motion of the fluid in the rotating frame), this energy is constant independent of position r. Requiring the energy to be constant, we obtain the parabolic form:
where h(0) is the height at r = 0 (the axis). See Figures 1 and 2.
The principle of operation of the centrifuge
also can be simply understood in terms of this expression for the
potential energy, which shows that it is favorable energetically when
the volume far from the axis of rotation is occupied by the heavier
substance.