Action potential

From Wikipedia, the free encyclopedia

As an action potential (nerve impulse) travels down an axon there is a change in polarity across the membrane of the axon. In response to a signal from another neuron, sodium- (Na⁺) and potassium- (K⁺) gated ion channels open and close as the membrane reaches its threshold potential. Na⁺ channels open at the beginning of the action potential, and Na⁺ moves into the axon, causing depolarization. Repolarization occurs when the K⁺ channels open and K⁺ moves out of the axon, creating a change in polarity between the outside of the cell and the inside. The impulse travels down the axon in one direction only, to the axon terminal where it signals other neurons.

In physiology, an action potential occurs when the membrane potential of a specific axon location rapidly rises and falls: this depolarisation then causes adjacent locations to similarly depolarise. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, endocrine cells, and in some plant cells.

In neurons, action potentials play a central role in cell-to-cell communication by providing for—or, with regard to saltatory conduction, assisting—the propagation of signals along the neuron's axon towards synaptic boutons situated at the ends of an axon; these signals can then connect with other neurons at synapses, or to motor cells or glands. In other types of cells, their main function is to activate intracellular processes. In muscle cells, for example, an action potential is the first step in the chain of events leading to contraction. In beta cells of the pancreas, they provoke release of insulin. Action potentials in neurons are also known as "nerve impulses" or "spikes", and the temporal sequence of action potentials generated by a neuron is called its "spike train". A neuron that emits an action potential, or nerve impulse, is often said to "fire".

Action potentials are generated by special types of voltage-gated ion channels embedded in a cell's plasma membrane. These channels are shut when the membrane potential is near the (negative) resting potential of the cell, but they rapidly begin to open if the membrane potential increases to a precisely defined threshold voltage, depolarising the transmembrane potential. When the channels open, they allow an inward flow of sodium ions, which changes the electrochemical gradient, which in turn produces a further rise in the membrane potential. This then causes more channels to open, producing a greater electric current across the cell membrane, and so on. The process proceeds explosively until all of the available ion channels are open, resulting in a large upswing in the membrane potential. The rapid influx of sodium ions causes the polarity of the plasma membrane to reverse, and the ion channels then rapidly inactivate. As the sodium channels close, sodium ions can no longer enter the neuron, and then they are actively transported back out of the plasma membrane. Potassium channels are then activated, and there is an outward current of potassium ions, returning the electrochemical gradient to the resting state. After an action potential has occurred, there is a transient negative shift, called the afterhyperpolarization. 

In animal cells, there are two primary types of action potentials. One type is generated by voltage-gated sodium channels, the other by voltage-gated calcium channels. Sodium-based action potentials usually last for under one millisecond, but calcium-based action potentials may last for 100 milliseconds or longer. In some types of neurons, slow calcium spikes provide the driving force for a long burst of rapidly emitted sodium spikes. In cardiac muscle cells, on the other hand, an initial fast sodium spike provides a "primer" to provoke the rapid onset of a calcium spike, which then produces muscle contraction.

In the Hodgkin–Huxley membrane capacitance model, the speed of transmission of an action potential was undefined and it was assumed that adjacent areas became depolarized due to released ion interference with neighboring channels. Measurements of ion diffusion and radii have since shown this not to be possible. Moreover, contradictory measurements of entropy changes and timing disputed the capacitance model as acting alone.

Overview

Shape of a typical action potential. The membrane potential remains near a baseline level until at some point in time, it abruptly spikes upward and then rapidly falls.

 

Nearly all cell membranes in animals, plants and fungi maintain a voltage difference between the exterior and interior of the cell, called the membrane potential. A typical voltage across an animal cell membrane is −70 mV. This means that the interior of the cell has a negative voltage of approximately one-fifteenth of a volt relative to the exterior. In most types of cells, the membrane potential usually stays fairly constant. Some types of cells, however, are electrically active in the sense that their voltages fluctuate over time. In some types of electrically active cells, including neurons and muscle cells, the voltage fluctuations frequently take the form of a rapid upward spike followed by a rapid fall. These up-and-down cycles are known as action potentials. In some types of neurons, the entire up-and-down cycle takes place in a few thousandths of a second. In muscle cells, a typical action potential lasts about a fifth of a second. In some other types of cells, and also in plants, an action potential may last three seconds or more.

The electrical properties of a cell are determined by the structure of the membrane that surrounds it. A cell membrane consists of a lipid bilayer of molecules in which larger protein molecules are embedded. The lipid bilayer is highly resistant to movement of electrically charged ions, so it functions as an insulator. The large membrane-embedded proteins, in contrast, provide channels through which ions can pass across the membrane. Action potentials are driven by channel proteins whose configuration switches between closed and open states as a function of the voltage difference between the interior and exterior of the cell. These voltage-sensitive proteins are known as voltage-gated ion channels. 

An in-depth process of how an action potential will pass through a neuron during neuron transmission including the 4 stages: resting potential, depolarization, re-polarization, and back to resting potential. The diagram shows how sodium ions and potassium ions interact to show how the changing of charge allows the action potential to cross with the use of facilitated diffusion and active transport.

Process in a typical neuron

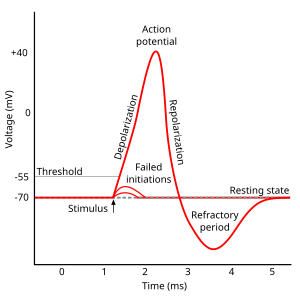
Approximate plot of a typical action potential shows its various phases as the action potential passes a point on a cell membrane. The membrane potential starts out at −70 mV at time zero. A stimulus is applied at time = 1 ms, which raises the membrane potential above −55 mV (the threshold potential). After the stimulus is applied, the membrane potential rapidly rises to a peak potential of +40 mV at time = 2 ms. Just as quickly, the potential then drops and overshoots to −90 mV at time = 3 ms, and finally the resting potential of −70 mV is reestablished at time = 5 ms.

 

All cells in animal body tissues are electrically polarized – in other words, they maintain a voltage difference across the cell's plasma membrane, known as the membrane potential. This electrical polarization results from a complex interplay between protein structures embedded in the membrane called ion pumps and ion channels. In neurons, the types of ion channels in the membrane usually vary across different parts of the cell, giving the dendrites, axon, and cell body different electrical properties. As a result, some parts of the membrane of a neuron may be excitable (capable of generating action potentials), whereas others are not. Recent studies have shown that the most excitable part of a neuron is the part after the axon hillock (the point where the axon leaves the cell body), which is called the initial segment, but the axon and cell body are also excitable in most cases.

Each excitable patch of membrane has two important levels of membrane potential: the resting potential, which is the value the membrane potential maintains as long as nothing perturbs the cell, and a higher value called the threshold potential. At the axon hillock of a typical neuron, the resting potential is around –70 millivolts (mV) and the threshold potential is around –55 mV. Synaptic inputs to a neuron cause the membrane to depolarize or hyperpolarize; that is, they cause the membrane potential to rise or fall. Action potentials are triggered when enough depolarization accumulates to bring the membrane potential up to threshold. When an action potential is triggered, the membrane potential abruptly shoots upward and then equally abruptly shoots back downward, often ending below the resting level, where it remains for some period of time. The shape of the action potential is stereotyped; this means that the rise and fall usually have approximately the same amplitude and time course for all action potentials in a given cell. (Exceptions are discussed later in the article). In most neurons, the entire process takes place in about a thousandth of a second. Many types of neurons emit action potentials constantly at rates of up to 10–100 per second. However, some types are much quieter, and may go for minutes or longer without emitting any action potentials.

Biophysical basis

Action potentials result from the presence in a cell's membrane of special types of voltage-gated ion channels. A voltage-gated ion channel is a cluster of proteins embedded in the membrane that has three key properties:

1. It is capable of assuming more than one conformation.
2. At least one of the conformations creates a channel through the membrane that is permeable to specific types of ions.
3. The transition between conformations is influenced by the membrane potential.

Thus, a voltage-gated ion channel tends to be open for some values of the membrane potential, and closed for others. In most cases, however, the relationship between membrane potential and channel state is probabilistic and involves a time delay. Ion channels switch between conformations at unpredictable times: The membrane potential determines the rate of transitions and the probability per unit time of each type of transition. 

Action potential propagation along an axon

Voltage-gated ion channels are capable of producing action potentials because they can give rise to positive feedback loops: The membrane potential controls the state of the ion channels, but the state of the ion channels controls the membrane potential. Thus, in some situations, a rise in the membrane potential can cause ion channels to open, thereby causing a further rise in the membrane potential. An action potential occurs when this positive feedback cycle proceeds explosively. The time and amplitude trajectory of the action potential are determined by the biophysical properties of the voltage-gated ion channels that produce it. Several types of channels capable of producing the positive feedback necessary to generate an action potential do exist. Voltage-gated sodium channels are responsible for the fast action potentials involved in nerve conduction. Slower action potentials in muscle cells and some types of neurons are generated by voltage-gated calcium channels. Each of these types comes in multiple variants, with different voltage sensitivity and different temporal dynamics.

The most intensively studied type of voltage-dependent ion channels comprises the sodium channels involved in fast nerve conduction. These are sometimes known as Hodgkin-Huxley sodium channels because they were first characterized by Alan Hodgkin and Andrew Huxley in their Nobel Prize-winning studies of the biophysics of the action potential, but can more conveniently be referred to as Na_V channels. (The "V" stands for "voltage".) An Na_V channel has three possible states, known as deactivated, activated, and inactivated. The channel is permeable only to sodium ions when it is in the activated state. When the membrane potential is low, the channel spends most of its time in the deactivated (closed) state. If the membrane potential is raised above a certain level, the channel shows increased probability of transitioning to the activated (open) state. The higher the membrane potential the greater the probability of activation. Once a channel has activated, it will eventually transition to the inactivated (closed) state. It tends then to stay inactivated for some time, but, if the membrane potential becomes low again, the channel will eventually transition back to the deactivated state. During an action potential, most channels of this type go through a cycle deactivated→activated→inactivated→deactivated. This is only the population average behavior, however — an individual channel can in principle make any transition at any time. However, the likelihood of a channel's transitioning from the inactivated state directly to the activated state is very low: A channel in the inactivated state is refractory until it has transitioned back to the deactivated state. 

The outcome of all this is that the kinetics of the Na_V channels are governed by a transition matrix whose rates are voltage-dependent in a complicated way. Since these channels themselves play a major role in determining the voltage, the global dynamics of the system can be quite difficult to work out. Hodgkin and Huxley approached the problem by developing a set of differential equations for the parameters that govern the ion channel states, known as the Hodgkin-Huxley equations. These equations have been extensively modified by later research, but form the starting point for most theoretical studies of action potential biophysics.

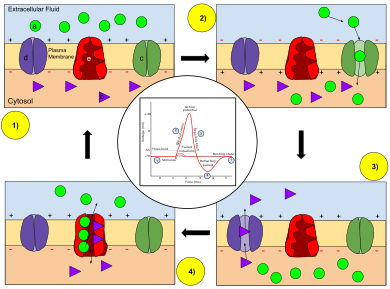
Ion movement during an action potential.
Key: a) Sodium (Na⁺) ion. b) Potassium (K⁺) ion. c) Sodium channel. d) Potassium channel. e) Sodium-potassium pump.
In the stages of an action potential, the permeability of the membrane of the neuron changes. At the resting state (1), sodium and potassium ions are unable to pass through the membrane, and the neuron has a negative charge inside (mainly due to the large proteins that are negatively charged). Once the action potential is triggered, the depolarization (2) of the neuron activates the sodium channel, allowing sodium ions to pass through the membrane of the neuron and results in a positive charge in the neuron and a negative charge in the extracellular fluid. After the action potential is reached, the neuron begins repolarization (3), where the sodium channels close and the potassium channels open, allowing potassium ions to cross the membrane and flood into the extracellular fluid, resulting in a positive charge in the extracellular fluid and a negative charge that is below the resting potential of the neuron. Finally, to return the neuron to that resting potential after the potassium pump closes, a sodium-potassium pump works to exchange three sodium ions per two potassium ions across the plasma membrane during the refractory period (4). Once the Na⁺ and K⁺ are back where they started, the neuron is back to its resting state (1), ready to repeat the process for the next action potential.

 

As the membrane potential is increased, sodium ion channels open, allowing the entry of sodium ions into the cell. This is followed by the opening of potassium ion channels that permit the exit of potassium ions from the cell. The inward flow of sodium ions increases the concentration of positively charged cations in the cell and causes depolarization, where the potential of the cell is higher than the cell's resting potential. The sodium channels close at the peak of the action potential, while potassium continues to leave the cell. The efflux of potassium ions decreases the membrane potential or hyperpolarizes the cell. For small voltage increases from rest, the potassium current exceeds the sodium current and the voltage returns to its normal resting value, typically −70 mV. However, if the voltage increases past a critical threshold, typically 15 mV higher than the resting value, the sodium current dominates. This results in a runaway condition whereby the positive feedback from the sodium current activates even more sodium channels. Thus, the cell fires, producing an action potential. The frequency at which a neuron elicits action potentials is often referred to as a firing rate or neural firing rate. 

Currents produced by the opening of voltage-gated channels in the course of an action potential are typically significantly larger than the initial stimulating current. Thus, the amplitude, duration, and shape of the action potential are determined largely by the properties of the excitable membrane and not the amplitude or duration of the stimulus. This all-or-nothing property of the action potential sets it apart from graded potentials such as receptor potentials, electrotonic potentials, and synaptic potentials, which scale with the magnitude of the stimulus. A variety of action potential types exist in many cell types and cell compartments as determined by the types of voltage-gated channels, leak channels, channel distributions, ionic concentrations, membrane capacitance, temperature, and other factors. 

The principal ions involved in an action potential are sodium and potassium cations; sodium ions enter the cell, and potassium ions leave, restoring equilibrium. Relatively few ions need to cross the membrane for the membrane voltage to change drastically. The ions exchanged during an action potential, therefore, make a negligible change in the interior and exterior ionic concentrations. The few ions that do cross are pumped out again by the continuous action of the sodium–potassium pump, which, with other ion transporters, maintains the normal ratio of ion concentrations across the membrane. Calcium cations and chloride anions are involved in a few types of action potentials, such as the cardiac action potential and the action potential in the single-cell alga Acetabularia, respectively. 

Although action potentials are generated locally on patches of excitable membrane, the resulting currents can trigger action potentials on neighboring stretches of membrane, precipitating a domino-like propagation. In contrast to passive spread of electric potentials (electrotonic potential), action potentials are generated anew along excitable stretches of membrane and propagate without decay. Myelinated sections of axons are not excitable and do not produce action potentials and the signal is propagated passively as electrotonic potential. Regularly spaced unmyelinated patches, called the nodes of Ranvier, generate action potentials to boost the signal. Known as saltatory conduction, this type of signal propagation provides a favorable tradeoff of signal velocity and axon diameter. Depolarization of axon terminals, in general, triggers the release of neurotransmitter into the synaptic cleft. In addition, backpropagating action potentials have been recorded in the dendrites of pyramidal neurons, which are ubiquitous in the neocortex. These are thought to have a role in spike-timing-dependent plasticity.

Maturation of the electrical properties of the action potential

A neuron's ability to generate and propagate an action potential changes during development. How much the membrane potential of a neuron changes as the result of a current impulse is a function of the membrane input resistance. As a cell grows, more channels are added to the membrane, causing a decrease in input resistance. A mature neuron also undergoes shorter changes in membrane potential in response to synaptic currents. Neurons from a ferret lateral geniculate nucleus have a longer time constant and larger voltage deflection at P0 than they do at P30. One consequence of the decreasing action potential duration is that the fidelity of the signal can be preserved in response to high frequency stimulation. Immature neurons are more prone to synaptic depression than potentiation after high frequency stimulation.

In the early development of many organisms, the action potential is actually initially carried by calcium current rather than sodium current. The opening and closing kinetics of calcium channels during development are slower than those of the voltage-gated sodium channels that will carry the action potential in the mature neurons. The longer opening times for the calcium channels can lead to action potentials that are considerably slower than those of mature neurons. Xenopus neurons initially have action potentials that take 60–90 ms. During development, this time decreases to 1 ms. There are two reasons for this drastic decrease. First, the inward current becomes primarily carried by sodium channels. Second, the delayed rectifier, a potassium channel current, increases to 3.5 times its initial strength.

In order for the transition from a calcium-dependent action potential to a sodium-dependent action potential to proceed new channels must be added to the membrane. If Xenopus neurons are grown in an environment with RNA synthesis or protein synthesis inhibitors that transition is prevented. Even the electrical activity of the cell itself may play a role in channel expression. If action potentials in Xenopus myocytes are blocked, the typical increase in sodium and potassium current density is prevented or delayed.

This maturation of electrical properties is seen across species. Xenopus sodium and potassium currents increase drastically after a neuron goes through its final phase of mitosis. The sodium current density of rat cortical neurons increases by 600% within the first two postnatal weeks.

Neurotransmission

Anatomy of a neuron

Structure of a typical neuron

Neuron
Dendrite Soma Axon Nucleus Node of Ranvier Axon terminal Schwann cell Myelin sheath

Several types of cells support an action potential, such as plant cells, muscle cells, and the specialized cells of the heart (in which occurs the cardiac action potential). However, the main excitable cell is the neuron, which also has the simplest mechanism for the action potential.

Neurons are electrically excitable cells composed, in general, of one or more dendrites, a single soma, a single axon and one or more axon terminals. Dendrites are cellular projections whose primary function is to receive synaptic signals. Their protrusions, known as dendritic spines, are designed to capture the neurotransmitters released by the presynaptic neuron. They have a high concentration of ligand-gated ion channels. These spines have a thin neck connecting a bulbous protrusion to the dendrite. This ensures that changes occurring inside the spine are less likely to affect the neighboring spines. The dendritic spine can, with rare exception, act as an independent unit. The dendrites extend from the soma, which houses the nucleus, and many of the "normal" eukaryotic organelles. Unlike the spines, the surface of the soma is populated by voltage activated ion channels. These channels help transmit the signals generated by the dendrites. Emerging out from the soma is the axon hillock. This region is characterized by having a very high concentration of voltage-activated sodium channels. In general, it is considered to be the spike initiation zone for action potentials,^[14] i.e. the trigger zone. Multiple signals generated at the spines, and transmitted by the soma all converge here. Immediately after the axon hillock is the axon. This is a thin tubular protrusion traveling away from the soma. The axon is insulated by a myelin sheath. Myelin is composed of either Schwann cells (in the peripheral nervous system) or oligodendrocytes (in the central nervous system), both of which are types of glial cells. Although glial cells are not involved with the transmission of electrical signals, they communicate and provide important biochemical support to neurons. To be specific, myelin wraps multiple times around the axonal segment, forming a thick fatty layer that prevents ions from entering or escaping the axon. This insulation prevents significant signal decay as well as ensuring faster signal speed. This insulation, however, has the restriction that no channels can be present on the surface of the axon. There are, therefore, regularly spaced patches of membrane, which have no insulation. These nodes of Ranvier can be considered to be "mini axon hillocks", as their purpose is to boost the signal in order to prevent significant signal decay. At the furthest end, the axon loses its insulation and begins to branch into several axon terminals. These presynaptic terminals, or synaptic boutons, are a specialized area within the axon of the presynaptic cell that contains neurotransmitters enclosed in small membrane-bound spheres called synaptic vesicles.

Initiation

Before considering the propagation of action potentials along axons and their termination at the synaptic knobs, it is helpful to consider the methods by which action potentials can be initiated at the axon hillock. The basic requirement is that the membrane voltage at the hillock be raised above the threshold for firing. There are several ways in which this depolarization can occur. 

When an action potential arrives at the end of the pre-synaptic axon (top), it causes the release of neurotransmitter molecules that open ion channels in the post-synaptic neuron (bottom). The combined excitatory and inhibitory postsynaptic potentials of such inputs can begin a new action potential in the post-synaptic neuron.

Dynamics

Action potentials are most commonly initiated by excitatory postsynaptic potentials from a presynaptic neuron. Typically, neurotransmitter molecules are released by the presynaptic neuron. These neurotransmitters then bind to receptors on the postsynaptic cell. This binding opens various types of ion channels. This opening has the further effect of changing the local permeability of the cell membrane and, thus, the membrane potential. If the binding increases the voltage (depolarizes the membrane), the synapse is excitatory. If, however, the binding decreases the voltage (hyperpolarizes the membrane), it is inhibitory. Whether the voltage is increased or decreased, the change propagates passively to nearby regions of the membrane (as described by the cable equation and its refinements). Typically, the voltage stimulus decays exponentially with the distance from the synapse and with time from the binding of the neurotransmitter. Some fraction of an excitatory voltage may reach the axon hillock and may (in rare cases) depolarize the membrane enough to provoke a new action potential. More typically, the excitatory potentials from several synapses must work together at nearly the same time to provoke a new action potential. Their joint efforts can be thwarted, however, by the counteracting inhibitory postsynaptic potentials. 

Neurotransmission can also occur through electrical synapses. Due to the direct connection between excitable cells in the form of gap junctions, an action potential can be transmitted directly from one cell to the next in either direction. The free flow of ions between cells enables rapid non-chemical-mediated transmission. Rectifying channels ensure that action potentials move only in one direction through an electrical synapse. Electrical synapses are found in all nervous systems, including the human brain, although they are a distinct minority.

"All-or-none" principle

The amplitude of an action potential is independent of the amount of current that produced it. In other words, larger currents do not create larger action potentials. Therefore, action potentials are said to be all-or-none signals, since either they occur fully or they do not occur at all. This is in contrast to receptor potentials, whose amplitudes are dependent on the intensity of a stimulus. In both cases, the frequency of action potentials is correlated with the intensity of a stimulus.

Sensory neurons

In sensory neurons, an external signal such as pressure, temperature, light, or sound is coupled with the opening and closing of ion channels, which in turn alter the ionic permeabilities of the membrane and its voltage. These voltage changes can again be excitatory (depolarizing) or inhibitory (hyperpolarizing) and, in some sensory neurons, their combined effects can depolarize the axon hillock enough to provoke action potentials. Some examples in humans include the olfactory receptor neuron and Meissner's corpuscle, which are critical for the sense of smell and touch, respectively. However, not all sensory neurons convert their external signals into action potentials; some do not even have an axon. Instead, they may convert the signal into the release of a neurotransmitter, or into continuous graded potentials, either of which may stimulate subsequent neuron(s) into firing an action potential. For illustration, in the human ear, hair cells convert the incoming sound into the opening and closing of mechanically gated ion channels, which may cause neurotransmitter molecules to be released. In similar manner, in the human retina, the initial photoreceptor cells and the next layer of cells (comprising bipolar cells and horizontal cells) do not produce action potentials; only some amacrine cells and the third layer, the ganglion cells, produce action potentials, which then travel up the optic nerve.

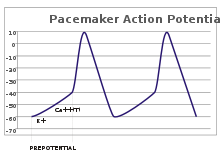
Pacemaker potentials

In pacemaker potentials, the cell spontaneously depolarizes (straight line with upward slope) until it fires an action potential.

 

In sensory neurons, action potentials result from an external stimulus. However, some excitable cells require no such stimulus to fire: They spontaneously depolarize their axon hillock and fire action potentials at a regular rate, like an internal clock. The voltage traces of such cells are known as pacemaker potentials. The cardiac pacemaker cells of the sinoatrial node in the heart provide a good example. Although such pacemaker potentials have a natural rhythm, it can be adjusted by external stimuli; for instance, heart rate can be altered by pharmaceuticals as well as signals from the sympathetic and parasympathetic nerves. The external stimuli do not cause the cell's repetitive firing, but merely alter its timing. In some cases, the regulation of frequency can be more complex, leading to patterns of action potentials, such as bursting.

Phases

The course of the action potential can be divided into five parts: the rising phase, the peak phase, the falling phase, the undershoot phase, and the refractory period. During the rising phase the membrane potential depolarizes (becomes more positive). The point at which depolarization stops is called the peak phase. At this stage, the membrane potential reaches a maximum. Subsequent to this, there is a falling phase. During this stage the membrane potential becomes more negative, returning towards resting potential. The undershoot, or after hyperpolarization, phase is the period during which the membrane potential temporarily becomes more negatively charged than when at rest (hyperpolarized). Finally, the time during which a subsequent action potential is impossible or difficult to fire is called the refractory period, which may overlap with the other phases.

The course of the action potential is determined by two coupled effects. First, voltage-sensitive ion channels open and close in response to changes in the membrane voltage V_m. This changes the membrane's permeability to those ions. Second, according to the Goldman equation, this change in permeability changes the equilibrium potential E_m, and, thus, the membrane voltage V_m. Thus, the membrane potential affects the permeability, which then further affects the membrane potential. This sets up the possibility for positive feedback, which is a key part of the rising phase of the action potential. A complicating factor is that a single ion channel may have multiple internal "gates" that respond to changes in V_m in opposite ways, or at different rates. For example, although raising V_m opens most gates in the voltage-sensitive sodium channel, it also closes the channel's "inactivation gate", albeit more slowly. Hence, when V_m is raised suddenly, the sodium channels open initially, but then close due to the slower inactivation.

The voltages and currents of the action potential in all of its phases were modeled accurately by Alan Lloyd Hodgkin and Andrew Huxley in 1952, for which they were awarded the Nobel Prize in Physiology or Medicine in 1963. However, their model considers only two types of voltage-sensitive ion channels, and makes several assumptions about them, e.g., that their internal gates open and close independently of one another. In reality, there are many types of ion channels, and they do not always open and close independently.

Stimulation and rising phase

A typical action potential begins at the axon hillock with a sufficiently strong depolarization, e.g., a stimulus that increases V_m. This depolarization is often caused by the injection of extra sodium cations into the cell; these cations can come from a wide variety of sources, such as chemical synapses, sensory neurons or pacemaker potentials.

For a neuron at rest, there is a high concentration of sodium and chloride ions in the extracellular fluid compared to the intracellular fluid while there is a high concentration of potassium ions in the intracellular fluid compared to the extracellular fluid. This concentration gradient along with potassium leak channels present on the membrane of the neuron causes an efflux of potassium ions making the resting potential close to E_K ≈ –75 mV. The depolarization opens both the sodium and potassium channels in the membrane, allowing the ions to flow into and out of the axon, respectively. If the depolarization is small (say, increasing V_m from −70 mV to −60 mV), the outward potassium current overwhelms the inward sodium current and the membrane repolarizes back to its normal resting potential around −70 mV. However, if the depolarization is large enough, the inward sodium current increases more than the outward potassium current and a runaway condition (positive feedback) results: the more inward current there is, the more V_m increases, which in turn further increases the inward current. A sufficiently strong depolarization (increase in V_m) causes the voltage-sensitive sodium channels to open; the increasing permeability to sodium drives V_m closer to the sodium equilibrium voltage E_Na≈ +55 mV. The increasing voltage in turn causes even more sodium channels to open, which pushes V_m still further towards E_Na. This positive feedback continues until the sodium channels are fully open and V_m is close to E_Na. The sharp rise in V_m and sodium permeability correspond to the rising phase of the action potential.

The critical threshold voltage for this runaway condition is usually around −45 mV, but it depends on the recent activity of the axon. A membrane that has just fired an action potential cannot fire another one immediately, since the ion channels have not returned to the deactivated state. The period during which no new action potential can be fired is called the absolute refractory period. At longer times, after some but not all of the ion channels have recovered, the axon can be stimulated to produce another action potential, but with a higher threshold, requiring a much stronger depolarization, e.g., to −30 mV. The period during which action potentials are unusually difficult to evoke is called the relative refractory period.

Peak and falling phase

The positive feedback of the rising phase slows and comes to a halt as the sodium ion channels become maximally open. At the peak of the action potential, the sodium permeability is maximized and the membrane voltage V_m is nearly equal to the sodium equilibrium voltage E_Na. However, the same raised voltage that opened the sodium channels initially also slowly shuts them off, by closing their pores; the sodium channels become inactivated. This lowers the membrane's permeability to sodium relative to potassium, driving the membrane voltage back towards the resting value. At the same time, the raised voltage opens voltage-sensitive potassium channels; the increase in the membrane's potassium permeability drives V_m towards E_K. Combined, these changes in sodium and potassium permeability cause V_m to drop quickly, repolarizing the membrane and producing the "falling phase" of the action potential.

After hyperpolarization

The raised voltage opened many more potassium channels than usual, and some of these do not close right away when the membrane returns to its normal resting voltage. In addition, further potassium channels open in response to the influx of calcium ions during the action potential. The potassium permeability of the membrane is transiently unusually high, driving the membrane voltage V_m even closer to the potassium equilibrium voltage E_K. Hence, there is an undershoot or hyperpolarization, termed an afterhyperpolarization in technical language, that persists until the membrane potassium permeability returns to its usual value.

Refractory period

Each action potential is followed by a refractory period, which can be divided into an absolute refractory period, during which it is impossible to evoke another action potential, and then a relative refractory period, during which a stronger-than-usual stimulus is required. These two refractory periods are caused by changes in the state of sodium and potassium channel molecules. When closing after an action potential, sodium channels enter an "inactivated" state, in which they cannot be made to open regardless of the membrane potential—this gives rise to the absolute refractory period. Even after a sufficient number of sodium channels have transitioned back to their resting state, it frequently happens that a fraction of potassium channels remains open, making it difficult for the membrane potential to depolarize, and thereby giving rise to the relative refractory period. Because the density and sub-types of potassium channels may differ greatly between different types of neurons, the duration of the relative refractory period is highly variable.

The absolute refractory period is largely responsible for the unidirectional propagation of action potentials along axons. At any given moment, the patch of axon behind the actively spiking part is refractory, but the patch in front, not having been activated recently, is capable of being stimulated by the depolarization from the action potential.

Propagation

The action potential generated at the axon hillock propagates as a wave along the axon. The currents flowing inwards at a point on the axon during an action potential spread out along the axon, and depolarize the adjacent sections of its membrane. If sufficiently strong, this depolarization provokes a similar action potential at the neighboring membrane patches. This basic mechanism was demonstrated by Alan Lloyd Hodgkin in 1937. After crushing or cooling nerve segments and thus blocking the action potentials, he showed that an action potential arriving on one side of the block could provoke another action potential on the other, provided that the blocked segment was sufficiently short.

Once an action potential has occurred at a patch of membrane, the membrane patch needs time to recover before it can fire again. At the molecular level, this absolute refractory period corresponds to the time required for the voltage-activated sodium channels to recover from inactivation, i.e., to return to their closed state. There are many types of voltage-activated potassium channels in neurons. Some of them inactivate fast (A-type currents) and some of them inactivate slowly or not inactivate at all; this variability guarantees that there will be always an available source of current for repolarization, even if some of the potassium channels are inactivated because of preceding depolarization. On the other hand, all neuronal voltage-activated sodium channels inactivate within several milliseconds during strong depolarization, thus making following depolarization impossible until a substantial fraction of sodium channels have returned to their closed state. Although it limits the frequency of firing, the absolute refractory period ensures that the action potential moves in only one direction along an axon. The currents flowing in due to an action potential spread out in both directions along the axon. However, only the unfired part of the axon can respond with an action potential; the part that has just fired is unresponsive until the action potential is safely out of range and cannot restimulate that part. In the usual orthodromic conduction, the action potential propagates from the axon hillock towards the synaptic knobs (the axonal termini); propagation in the opposite direction—known as antidromic conduction—is very rare. However, if a laboratory axon is stimulated in its middle, both halves of the axon are "fresh", i.e., unfired; then two action potentials will be generated, one traveling towards the axon hillock and the other traveling towards the synaptic knobs.

Myelin and saltatory conduction

In saltatory conduction, an action potential at one node of Ranvier causes inwards currents that depolarize the membrane at the next node, provoking a new action potential there; the action potential appears to "hop" from node to node.

 

In order to enable fast and efficient transduction of electrical signals in the nervous system, certain neuronal axons are covered with myelin sheaths. Myelin is a multilamellar membrane that enwraps the axon in segments separated by intervals known as nodes of Ranvier. It is produced by specialized cells: Schwann cells exclusively in the peripheral nervous system, and oligodendrocytes exclusively in the central nervous system. Myelin sheath reduces membrane capacitance and increases membrane resistance in the inter-node intervals, thus allowing a fast, saltatory movement of action potentials from node to node. Myelination is found mainly in vertebrates, but an analogous system has been discovered in a few invertebrates, such as some species of shrimp. Not all neurons in vertebrates are myelinated; for example, axons of the neurons comprising the autonomous nervous system are not, in general, myelinated. 

Myelin prevents ions from entering or leaving the axon along myelinated segments. As a general rule, myelination increases the conduction velocity of action potentials and makes them more energy-efficient. Whether saltatory or not, the mean conduction velocity of an action potential ranges from 1 meter per second (m/s) to over 100 m/s, and, in general, increases with axonal diameter.

Action potentials cannot propagate through the membrane in myelinated segments of the axon. However, the current is carried by the cytoplasm, which is sufficient to depolarize the first or second subsequent node of Ranvier. Instead, the ionic current from an action potential at one node of Ranvier provokes another action potential at the next node; this apparent "hopping" of the action potential from node to node is known as saltatory conduction. Although the mechanism of saltatory conduction was suggested in 1925 by Ralph Lillie, the first experimental evidence for saltatory conduction came from Ichiji Tasaki and Taiji Takeuchi and from Andrew Huxley and Robert Stämpfli. By contrast, in unmyelinated axons, the action potential provokes another in the membrane immediately adjacent, and moves continuously down the axon like a wave. 

Comparison of the conduction velocities of myelinated and unmyelinated axons in the cat. The conduction velocity v of myelinated neurons varies roughly linearly with axon diameter d (that is, v ∝ d), whereas the speed of unmyelinated neurons varies roughly as the square root (v ∝√d). The red and blue curves are fits of experimental data, whereas the dotted lines are their theoretical extrapolations.

 

Myelin has two important advantages: fast conduction speed and energy efficiency. For axons larger than a minimum diameter (roughly 1 micrometre), myelination increases the conduction velocity of an action potential, typically tenfold. Conversely, for a given conduction velocity, myelinated fibers are smaller than their unmyelinated counterparts. For example, action potentials move at roughly the same speed (25 m/s) in a myelinated frog axon and an unmyelinated squid giant axon, but the frog axon has a roughly 30-fold smaller diameter and 1000-fold smaller cross-sectional area. Also, since the ionic currents are confined to the nodes of Ranvier, far fewer ions "leak" across the membrane, saving metabolic energy. This saving is a significant selective advantage, since the human nervous system uses approximately 20% of the body's metabolic energy.

The length of axons' myelinated segments is important to the success of saltatory conduction. They should be as long as possible to maximize the speed of conduction, but not so long that the arriving signal is too weak to provoke an action potential at the next node of Ranvier. In nature, myelinated segments are generally long enough for the passively propagated signal to travel for at least two nodes while retaining enough amplitude to fire an action potential at the second or third node. Thus, the safety factor of saltatory conduction is high, allowing transmission to bypass nodes in case of injury. However, action potentials may end prematurely in certain places where the safety factor is low, even in unmyelinated neurons; a common example is the branch point of an axon, where it divides into two axons.

Some diseases degrade myelin and impair saltatory conduction, reducing the conduction velocity of action potentials. The most well-known of these is multiple sclerosis, in which the breakdown of myelin impairs coordinated movement.

Cable theory

Cable theory's simplified view of a neuronal fiber. The connected RC circuits correspond to adjacent segments of a passive neurite. The extracellular resistances r_e (the counterparts of the intracellular resistances r_i) are not shown, since they are usually negligibly small; the extracellular medium may be assumed to have the same voltage everywhere.

 

The flow of currents within an axon can be described quantitatively by cable theory and its elaborations, such as the compartmental model. Cable theory was developed in 1855 by Lord Kelvin to model the transatlantic telegraph cable and was shown to be relevant to neurons by Hodgkin and Rushton in 1946. In simple cable theory, the neuron is treated as an electrically passive, perfectly cylindrical transmission cable, which can be described by a partial differential equation. 

${\displaystyle \tau {\frac {\partial V}{\partial t}}=\lambda ^{2}{\frac {\partial ^{2}V}{\partial x^{2}}}-V}$

where V(x, t) is the voltage across the membrane at a time t and a position x along the length of the neuron, and where λ and τ are the characteristic length and time scales on which those voltages decay in response to a stimulus. Referring to the circuit diagram on the right, these scales can be determined from the resistances and capacitances per unit length.

${\displaystyle \tau =\ r_{m}c_{m}\,}$

${\displaystyle \lambda ={\sqrt {\frac {r_{m}}{r_{\ell }}}}}$

These time and length-scales can be used to understand the dependence of the conduction velocity on the diameter of the neuron in un-myelinated fibers. For example, the time-scale τ increases with both the membrane resistance r_m and capacitance c_m. As the capacitance increases, more charge must be transferred to produce a given trans-membrane voltage (by the equation Q = CV); as the resistance increases, less charge is transferred per unit time, making the equilibration slower. In a similar manner, if the internal resistance per unit length r_i is lower in one axon than in another (e.g., because the radius of the former is larger), the spatial decay length λ becomes longer and the conduction velocity of an action potential should increase. If the trans-membrane resistance r_m is increased, that lowers the average "leakage" current across the membrane, likewise causing λ to become longer, increasing the conduction velocity.

Termination

Chemical synapses

In general, action potentials that reach the synaptic knobs cause a neurotransmitter to be released into the synaptic cleft. Neurotransmitters are small molecules that may open ion channels in the postsynaptic cell; most axons have the same neurotransmitter at all of their termini. The arrival of the action potential opens voltage-sensitive calcium channels in the presynaptic membrane; the influx of calcium causes vesicles filled with neurotransmitter to migrate to the cell's surface and release their contents into the synaptic cleft. This complex process is inhibited by the neurotoxins tetanospasmin and botulinum toxin, which are responsible for tetanus and botulism, respectively.

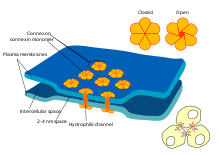
Electrical synapses between excitable cells allow ions to pass directly from one cell to another, and are much faster than chemical synapses.

Electrical synapses

Some synapses dispense with the "middleman" of the neurotransmitter, and connect the presynaptic and postsynaptic cells together. When an action potential reaches such a synapse, the ionic currents flowing into the presynaptic cell can cross the barrier of the two cell membranes and enter the postsynaptic cell through pores known as connexons. Thus, the ionic currents of the presynaptic action potential can directly stimulate the postsynaptic cell. Electrical synapses allow for faster transmission because they do not require the slow diffusion of neurotransmitters across the synaptic cleft. Hence, electrical synapses are used whenever fast response and coordination of timing are crucial, as in escape reflexes, the retina of vertebrates, and the heart.

Neuromuscular junctions

A special case of a chemical synapse is the neuromuscular junction, in which the axon of a motor neuron terminates on a muscle fiber. In such cases, the released neurotransmitter is acetylcholine, which binds to the acetylcholine receptor, an integral membrane protein in the membrane (the sarcolemma) of the muscle fiber. However, the acetylcholine does not remain bound; rather, it dissociates and is hydrolyzed by the enzyme, acetylcholinesterase, located in the synapse. This enzyme quickly reduces the stimulus to the muscle, which allows the degree and timing of muscular contraction to be regulated delicately. Some poisons inactivate acetylcholinesterase to prevent this control, such as the nerve agents sarin and tabun, and the insecticides diazinon and malathion.

Other cell types

Cardiac action potentials

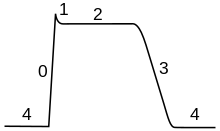
Phases of a cardiac action potential. The sharp rise in voltage ("0") corresponds to the influx of sodium ions, whereas the two decays ("1" and "3", respectively) correspond to the sodium-channel inactivation and the repolarizing eflux of potassium ions. The characteristic plateau ("2") results from the opening of voltage-sensitive calcium channels.

 

The cardiac action potential differs from the neuronal action potential by having an extended plateau, in which the membrane is held at a high voltage for a few hundred milliseconds prior to being repolarized by the potassium current as usual. This plateau is due to the action of slower calcium channels opening and holding the membrane voltage near their equilibrium potential even after the sodium channels have inactivated.

The cardiac action potential plays an important role in coordinating the contraction of the heart. The cardiac cells of the sinoatrial node provide the pacemaker potential that synchronizes the heart. The action potentials of those cells propagate to and through the atrioventricular node (AV node), which is normally the only conduction pathway between the atria and the ventricles. Action potentials from the AV node travel through the bundle of His and thence to the Purkinje fibers. Conversely, anomalies in the cardiac action potential—whether due to a congenital mutation or injury—can lead to human pathologies, especially arrhythmias. Several anti-arrhythmia drugs act on the cardiac action potential, such as quinidine, lidocaine, beta blockers, and verapamil.

Muscular action potentials

The action potential in a normal skeletal muscle cell is similar to the action potential in neurons. Action potentials result from the depolarization of the cell membrane (the sarcolemma), which opens voltage-sensitive sodium channels; these become inactivated and the membrane is repolarized through the outward current of potassium ions. The resting potential prior to the action potential is typically −90mV, somewhat more negative than typical neurons. The muscle action potential lasts roughly 2–4 ms, the absolute refractory period is roughly 1–3 ms, and the conduction velocity along the muscle is roughly 5 m/s. The action potential releases calcium ions that free up the tropomyosin and allow the muscle to contract. Muscle action potentials are provoked by the arrival of a pre-synaptic neuronal action potential at the neuromuscular junction, which is a common target for neurotoxins.

Plant action potentials

Plant and fungal cells  are also electrically excitable. The fundamental difference from animal action potentials is that the depolarization in plant cells is not accomplished by an uptake of positive sodium ions, but by release of negative chloride ions. Together with the following release of positive potassium ions, which is common to plant and animal action potentials, the action potential in plants infers, therefore, an osmotic loss of salt (KCl), whereas the animal action potential is osmotically neutral, when equal amounts of entering sodium and leaving potassium cancel each other osmotically. The interaction of electrical and osmotic relations in plant cells  indicates an osmotic function of electrical excitability in the common, unicellular ancestors of plants and animals under changing salinity conditions, whereas the present function of rapid signal transmission is seen as a younger accomplishment of metazoan cells in a more stable osmotic environment. It must be assumed that the familiar signalling function of action potentials in some vascular plants (e.g. Mimosa pudica) arose independently from that in metazoan excitable cells.

Taxonomic distribution and evolutionary advantages

Action potentials are found throughout multicellular organisms, including plants, invertebrates such as insects, and vertebrates such as reptiles and mammals. Sponges seem to be the main phylum of multicellular eukaryotes that does not transmit action potentials, although some studies have suggested that these organisms have a form of electrical signaling, too. The resting potential, as well as the size and duration of the action potential, have not varied much with evolution, although the conduction velocity does vary dramatically with axonal diameter and myelination. 

Comparison of action potentials (APs) from a representative cross-section of animals

Animal	Cell type	Resting potential (mV)	AP increase (mV)	AP duration (ms)	Conduction speed (m/s)
Squid (Loligo)	Giant axon	−60	120	0.75	35
Earthworm (Lumbricus)	Median giant fiber	−70	100	1.0	30
Cockroach (Periplaneta)	Giant fiber	−70	80–104	0.4	10
Frog (Rana)	Sciatic nerve axon	−60 to −80	110–130	1.0	7–30
Cat (Felis)	Spinal motor neuron	−55 to −80	80–110	1–1.5	30–120

Given its conservation throughout evolution, the action potential seems to confer evolutionary advantages. One function of action potentials is rapid, long-range signaling within the organism; the conduction velocity can exceed 110 m/s, which is one-third the speed of sound. For comparison, a hormone molecule carried in the bloodstream moves at roughly 8 m/s in large arteries. Part of this function is the tight coordination of mechanical events, such as the contraction of the heart. A second function is the computation associated with its generation. Being an all-or-none signal that does not decay with transmission distance, the action potential has similar advantages to digital electronics. The integration of various dendritic signals at the axon hillock and its thresholding to form a complex train of action potentials is another form of computation, one that has been exploited biologically to form central pattern generators and mimicked in artificial neural networks.

Experimental methods

Giant axons of the longfin inshore squid (Doryteuthis pealeii) were crucial for scientists to understand the action potential.

 

The study of action potentials has required the development of new experimental methods. The initial work, prior to 1955, was carried out primarily by Alan Lloyd Hodgkin and Andrew Fielding Huxley, who were, along John Carew Eccles, awarded the 1963 Nobel Prize in Physiology or Medicine for their contribution to the description of the ionic basis of nerve conduction. It focused on three goals: isolating signals from single neurons or axons, developing fast, sensitive electronics, and shrinking electrodes enough that the voltage inside a single cell could be recorded.

The first problem was solved by studying the giant axons found in the neurons of the squid (Loligo forbesii and Doryteuthis pealeii, at the time classified as Loligo pealeii). These axons are so large in diameter (roughly 1 mm, or 100-fold larger than a typical neuron) that they can be seen with the naked eye, making them easy to extract and manipulate. However, they are not representative of all excitable cells, and numerous other systems with action potentials have been studied.

The second problem was addressed with the crucial development of the voltage clamp, which permitted experimenters to study the ionic currents underlying an action potential in isolation, and eliminated a key source of electronic noise, the current I_C associated with the capacitance C of the membrane.^[60] Since the current equals C times the rate of change of the transmembrane voltage V_m, the solution was to design a circuit that kept V_m fixed (zero rate of change) regardless of the currents flowing across the membrane. Thus, the current required to keep V_m at a fixed value is a direct reflection of the current flowing through the membrane. Other electronic advances included the use of Faraday cages and electronics with high input impedance, so that the measurement itself did not affect the voltage being measured.

The third problem, that of obtaining electrodes small enough to record voltages within a single axon without perturbing it, was solved in 1949 with the invention of the glass micropipette electrode, which was quickly adopted by other researchers. Refinements of this method are able to produce electrode tips that are as fine as 100 Å (10 nm), which also confers high input impedance. Action potentials may also be recorded with small metal electrodes placed just next to a neuron, with neurochips containing EOSFETs, or optically with dyes that are sensitive to Ca²⁺ or to voltage.

As revealed by a patch clamp electrode, an ion channel has two states: open (high conductance) and closed (low conductance).

 

While glass micropipette electrodes measure the sum of the currents passing through many ion channels, studying the electrical properties of a single ion channel became possible in the 1970s with the development of the patch clamp by Erwin Neher and Bert Sakmann. For this discovery, they were awarded the Nobel Prize in Physiology or Medicine in 1991. Patch-clamping verified that ionic channels have discrete states of conductance, such as open, closed and inactivated.

Optical imaging technologies have been developed in recent years to measure action potentials, either via simultaneous multisite recordings or with ultra-spatial resolution. Using voltage-sensitive dyes, action potentials have been optically recorded from a tiny patch of cardiomyocyte membrane.

Neurotoxins

Tetrodotoxin is a lethal toxin found in pufferfish that inhibits the voltage-sensitive sodium channel, halting action potentials.

 

Several neurotoxins, both natural and synthetic, are designed to block the action potential. Tetrodotoxin from the pufferfish and saxitoxin from the Gonyaulax (the dinoflagellate genus responsible for "red tides") block action potentials by inhibiting the voltage-sensitive sodium channel; similarly, dendrotoxin from the black mamba snake inhibits the voltage-sensitive potassium channel. Such inhibitors of ion channels serve an important research purpose, by allowing scientists to "turn off" specific channels at will, thus isolating the other channels' contributions; they can also be useful in purifying ion channels by affinity chromatography or in assaying their concentration. However, such inhibitors also make effective neurotoxins, and have been considered for use as chemical weapons. Neurotoxins aimed at the ion channels of insects have been effective insecticides; one example is the synthetic permethrin, which prolongs the activation of the sodium channels involved in action potentials. The ion channels of insects are sufficiently different from their human counterparts that there are few side effects in humans.

History

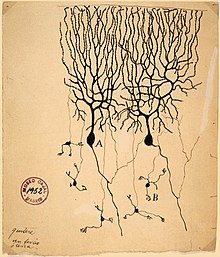
Image of two Purkinje cells (labeled as A) drawn by Santiago Ramón y Cajal in 1899. Large trees of dendrites feed into the soma, from which a single axon emerges and moves generally downwards with a few branch points. The smaller cells labeled B are granule cells.

 

The role of electricity in the nervous systems of animals was first observed in dissected frogs by Luigi Galvani, who studied it from 1791 to 1797. Galvani's results stimulated Alessandro Volta to develop the Voltaic pile—the earliest-known electric battery—with which he studied animal electricity (such as electric eels) and the physiological responses to applied direct-current voltages.

Scientists of the 19th century studied the propagation of electrical signals in whole nerves (i.e., bundles of neurons) and demonstrated that nervous tissue was made up of cells, instead of an interconnected network of tubes (a reticulum). Carlo Matteucci followed up Galvani's studies and demonstrated that cell membranes had a voltage across them and could produce direct current. Matteucci's work inspired the German physiologist, Emil du Bois-Reymond, who discovered the action potential in 1843. The conduction velocity of action potentials was first measured in 1850 by du Bois-Reymond's friend, Hermann von Helmholtz. To establish that nervous tissue is made up of discrete cells, the Spanish physician Santiago Ramón y Cajal and his students used a stain developed by Camillo Golgi to reveal the myriad shapes of neurons, which they rendered painstakingly. For their discoveries, Golgi and Ramón y Cajal were awarded the 1906 Nobel Prize in Physiology. Their work resolved a long-standing controversy in the neuroanatomy of the 19th century; Golgi himself had argued for the network model of the nervous system. 

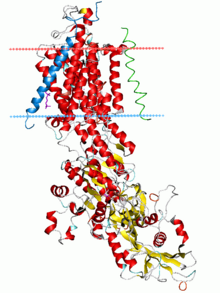
Ribbon diagram of the sodium–potassium pump in its E2-Pi state. The estimated boundaries of the lipid bilayer are shown as blue (intracellular) and red (extracellular) planes.

 

The 20th century was a significant era for electrophysiology. In 1902 and again in 1912, Julius Bernstein advanced the hypothesis that the action potential resulted from a change in the permeability of the axonal membrane to ions. Bernstein's hypothesis was confirmed by Ken Cole and Howard Curtis, who showed that membrane conductance increases during an action potential. In 1907, Louis Lapicque suggested that the action potential was generated as a threshold was crossed, what would be later shown as a product of the dynamical systems of ionic conductances. In 1949, Alan Hodgkin and Bernard Katz refined Bernstein's hypothesis by considering that the axonal membrane might have different permeabilities to different ions; in particular, they demonstrated the crucial role of the sodium permeability for the action potential. They made the first actual recording of the electrical changes across the neuronal membrane that mediate the action potential. This line of research culminated in the five 1952 papers of Hodgkin, Katz and Andrew Huxley, in which they applied the voltage clamp technique to determine the dependence of the axonal membrane's permeabilities to sodium and potassium ions on voltage and time, from which they were able to reconstruct the action potential quantitatively. Hodgkin and Huxley correlated the properties of their mathematical model with discrete ion channels that could exist in several different states, including "open", "closed", and "inactivated". Their hypotheses were confirmed in the mid-1970s and 1980s by Erwin Neher and Bert Sakmann, who developed the technique of patch clamping to examine the conductance states of individual ion channels. In the 21st century, researchers are beginning to understand the structural basis for these conductance states and for the selectivity of channels for their species of ion, through the atomic-resolution crystal structures, fluorescence distance measurements and cryo-electron microscopy studies.

Julius Bernstein was also the first to introduce the Nernst equation for resting potential across the membrane; this was generalized by David E. Goldman to the eponymous Goldman equation in 1943. The sodium–potassium pump was identified in 1957 and its properties gradually elucidated, culminating in the determination of its atomic-resolution structure by X-ray crystallography. The crystal structures of related ionic pumps have also been solved, giving a broader view of how these molecular machines work.

Quantitative models

Equivalent electrical circuit for the Hodgkin–Huxley model of the action potential. I_m and V_m represent the current through, and the voltage across, a small patch of membrane, respectively. The C_m represents the capacitance of the membrane patch, whereas the four g's represent the conductances of four types of ions. The two conductances on the left, for potassium (K) and sodium (Na), are shown with arrows to indicate that they can vary with the applied voltage, corresponding to the voltage-sensitive ion channels. The two conductances on the right help determine the resting membrane potential.

 

Mathematical and computational models are essential for understanding the action potential, and offer predictions that may be tested against experimental data, providing a stringent test of a theory. The most important and accurate of the early neural models is the Hodgkin–Huxley model, which describes the action potential by a coupled set of four ordinary differential equations (ODEs). Although the Hodgkin–Huxley model may be a simplification with few limitations compared to the realistic nervous membrane as it exists in nature, its complexity has inspired several even-more-simplified models, such as the Morris–Lecar model and the FitzHugh–Nagumo model, both of which have only two coupled ODEs. The properties of the Hodgkin–Huxley and FitzHugh–Nagumo models and their relatives, such as the Bonhoeffer–van der Pol model, have been well-studied within mathematics, computation and electronics. However the simple models of generator potential and action potential fail to accurately reproduce the near threshold neural spike rate and spike shape, specifically for the mechanoreceptors like the Pacinian corpuscle. More modern research has focused on larger and more integrated systems; by joining action-potential models with models of other parts of the nervous system (such as dendrites and synapses), researchers can study neural computation and simple reflexes, such as escape reflexes and others controlled by central pattern generators.

Nervous system network models

From Wikipedia, the free encyclopedia

Network of human nervous system comprises nodes (for example, neurons) that are connected by links (for example, synapses). The connectivity may be viewed anatomically, functionally, or electrophysiologically. These are presented in several Wikipedia articles that include Connectionism (a.k.a. Parallel Distributed Processing (PDP)), Biological neural network, Artificial neural network (a.k.a. Neural network), Computational neuroscience, as well as in several books by Ascoli, G. A. (2002), Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011), Gerstner, W., & Kistler, W. (2002), and Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986) among others. The focus of this article is a comprehensive view of modeling a neural network (technically neuronal network based on neuron model). Once an approach based on the perspective and connectivity is chosen, the models are developed at microscopic (ion and neuron), mesoscopic (functional or population), or macroscopic (system) levels. Computational modeling refers to models that are developed using computing tools.

Introduction

The nervous system consists networks made up of neurons and synapses connected to and controlling tissues as well as impacting human thoughts and behavior. In modeling neural networks of the nervous system one has to consider many factors. The brain and the neural network should be considered as an integrated and self-contained firmware system that includes hardware (organs), software (programs), memory (short term and long term), database (centralized and distributed), and a complex network of active elements (such as neurons, synapses, and tissues) and passive elements (such as parts of visual and auditory system) that carry information within and in-and-out of the body.

Why does one want to model the brain and neural network? Although highly sophisticated computer systems have been developed and used in all walks of life, they are nowhere close to the human system in hardware and software capabilities. So, scientists have been at work to understand the human operation system and try to simulate its functionalities. In order to accomplish this, one needs to model its components and functions and validate its performance with real life. Computational models of a well simulated nervous system enable learning the nervous system and apply it to real life problem solutions.

What is brain and what is neural network? "Network connectivity and models" below addresses the former question from an evolutionary perspective. The answer to the second question is based on the neural doctrine proposed by Ramon y Cajal (1894). He hypothesized that the elementary biological unit is an active cell, called neuron, and the human machine is run by a vast network that connects these neurons, called neural (or neuronal) network. The neural network is integrated with the human organs to form the human machine comprising the nervous system. 

Innumerable number of models of various aspects of the nervous system has been developed and there are several Wikipedia articles identified above that have been generated on the subject. The purpose of this article is to present a comprehensive view of all the models and provide the reader, especially a novice, to the neuroscience, with reference to the various sources.

Network characteristics

The basic structural unit of the neural network is connectivity of one neuron to another via an active junction, called synapse. Neurons of widely divergent characteristics are connected to each other via synapses, whose characteristics are also of diverse chemical and electrical properties. In presenting a comprehensive view of all possible modeling of the brain and neural network, an approach is to organize the material based on the characteristics of the networks and the goals that need to be accomplished. The latter could be either for understanding the brain and the nervous system better or to apply the knowledge gained from the total or partial nervous system to real world applications such as artificial intelligence, Neuroethics or improvements in medical science for society.

Network connectivity and models

On a high level representation, the neurons can be viewed as connected to other neurons to form a neural network in one of three ways. A specific network can be represented as a physiologically (or anatomically) connected network and modeled that way. There are several approaches to this (see Ascoli, G.A. (2002) Sporns, O. (2007), Connectionism, Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986), Arbib, M. A. (2007)). Or, it can form a functional network that serves a certain function and modeled accordingly (Honey, C. J., Kotter, R., Breakspear, R., & Sporns, O. (2007), Arbib, M. A. (2007)). A third way is to hypothesize a theory of the functioning of the biological components of the neural system by a mathematical model, in the form of a set of mathematical equations. The variables of the equation are some or all of the neurobiological properties of the entity being modeled, such as the dimensions of the dendrite or the stimulation rate of action potential along the axon in a neuron. The mathematical equations are solved using computational techniques and the results are validated with either simulation or experimental processes. This approach to modeling is called computational neuroscience. This methodology is used to model components from the ionic level to system level of the brain. This method is applicable for modeling integrated system of biological components that carry information signal from one neuron to another via intermediate active neurons that can pass the signal through or create new or additional signals. The computational neuroscience approach is extensively used and is based on two generic models, one of cell membrane potential Goldman (1943) and Hodgkin and Katz (1949), and the other based on Hodgkin-Huxley model of action potential (information signal).

Modeling levels

Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) classify the biological model of neuroscience into nine levels from ion channels to nervous system level based on size and function. Table 1 is based on this for neuronal networks. 

Level	Size	Description and Functions
Nervous system	> 1 m	Total system controlling thought, behavior, and sensory & motor functions
Subsystem	10 cm	Subsystem associated with one or more functions
Neural network	1 cm	Neural networks for system, subsystem, and functions
Microcircuit	1 mm	Networks of multilevel neurons, e.g., visual subsystem
Neuron	100 µm	Elementary biological unit of neuronal network
Dendric subunit	10 µm	Arbor of receptors in neuron
Synapse	1 µm	Junction or connectivity between neurons
Signalling pathway	1 nm	Link between connecting neurons
Ion channels	1 pm	Channels that act as gateway causing voltage change

Sporns, O. (2007) presents in his article on brain connectivity, modeling based on structural and functional types. A network that connects at neuron and synaptic level falls into the microscale. If the neurons are grouped into population of columns and minicolumns, the level is defined as mesoscale. The macroscale representation considers the network as regions of the brain connected by inter-regional pathways.

Arbib, M. A. (2007) considers in the modular model, a hierarchical formulation of the system into modules and sub-modules.

Signaling modes

The neuronal signal comprises a stream of short electrical pulses of about 100 millivolt amplitude and about 1 to 2 millisecond duration (Gerstner, W., & Kistler, W. (2002) Chapter 1). The individual pulses are action potentials or spikes and the chain of pulses is called spike train. The action potential does not contain any information. A combination of the timing of the start of the spike train, the rate or frequency of the spikes, and the number and pattern of spikes in the spike train determine the coding of the information content or the signal message.

The neuron cell has three components – dendrites, soma, and axon as shown in Figure 1. Dendrites, which have the shape of a tree with branches, called arbor, receive the message from other neurons with which the neuron is connected via synapses. The action potential received by each dendrite from the synapse is called the postsynaptic potential. The cumulative sum of the postsynaptic potentials is fed to the soma. The ionic components of the fluid inside and outside maintain the cell membrane at a resting potential of about 65 millivolts. When the cumulative postsynaptic potential exceeds the resting potential, an action potential is generated by the cell body or soma and propagated along the axon. The axon may have one or more terminals and these terminals transmit neurotransmitters to the synapses with which the neuron is connected. Depending on the stimulus received by the dendrites, soma may generate one or more well-separated action potentials or spike train. If the stimulus drives the membrane to a positive potential, it is an excitatory neuron; and if it drives the resting potential further in the negative direction, it is an inhibitory neuron.

Figure 1. Neuron anatomy for network model

 

The generation of the action potential is called the “firing.” The firing neuron described above is called a spiking neuron. We will model the electrical circuit of the neuron in Section 3.6. There are two types of spiking neurons. If the stimulus remains above the threshold level and the output is a spike train, it is called the Integrate-and-Fire (IF) neuron model. If output is modeled as dependent on the impulse response of the circuit, then it is called the Spike Response Model (SRM) (Gestner, W. (1995)). 

The spiking neuron model assumes that frequency (inverse of the rate at which spikes are generated) of spiking train starts at 0 and increases with the stimulus current. There is another hypothetical model that formulates the firing to happen at the threshold, but there is a quantum jump in frequency in contrast to smooth rise in frequency as in the spiking neuron model. This model is called the rate model. Gerstner, W., & Kistler, W. (2002), and Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) are good sources for a detailed treatment of spiking neuron models and rate neuron models.

Biological vs. artificial neural network

The concept of artificial neural network (ANN) was introduced by McColloch, W. S. & Pitts, W. (1943) for models based on behavior of biological neurons. Norbert Wiener (1961)  gave this new field the popular name of cybernetics, whose principle is the interdisciplinary relationship among engineering, biology, control systems, brain functions, and computer science. With the computer science field advancing, the von Neumann-type computer was introduced early in the neuroscience study. But it was not suitable for symbolic processing, nondeterministic computations, dynamic executions, parallel distributed processing, and management of extensive knowledge bases, which are needed for biological neural network applications; and the direction of mind-like machine development changed to a learning machine. Computing technology has since advanced extensively and computational neuroscience is now able to handle mathematical models developed for biological neural network. Research and development are progressing in both artificial and biological neural networks including efforts to merge the two.

Nervous system models

Evolutionary brain model

The “triune theory of the brain” McLean, P. (2003) is one of several models used to theorize the organizational structure of the brain. The most ancient neural structure of the brain is the brain stem or “lizard brain.” The second phase is limbic or paleo-mammalian brain and performs the four functions needed for animal survival – fighting, feeding, fleeing, and fornicating. The third phase is the neocortex or the neo-mammalian brain. The higher cognitive functions which distinguish humans from other animals are primarily in the cortex. The reptilian brain controls muscles, balance, and autonomic functions, such as breathing and heartbeat. This part of the brain is active, even in deep sleep. The limbic system includes the hypothalamus, hippocampus, and amygdala. The neocortex includes the cortex and the cerebrum. It corresponds to the brain of primates and, specifically, the human species. Each of the three brains is connected by nerves to the other two, but each seems to operate as its own brain system with distinct capacities.

PDP / connectionist model

The connectionist model evolved out of Parallel Distributed Processing framework that formulates a metatheory from which specific models can be generated for specific applications. PDP approach (Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986)) is a distributed parallel processing of many inter-related operations, somewhat similar to what’s happening in the human nervous system. The individual entities are defined as units and the units are connected to form a network. Thus, in the application to nervous system, one representation could be such that the units are the neurons and the links are the synapses.

Brain connectivity model

There are three types of brain connectivity models of a network (Sporns, O. (2007)). “Anatomical (or structural) connectivity” describes a network with anatomical links having specified relationship between connected “units.” If the dependent properties are stochastic, it is defined as “functional connectivity.” “Effective connectivity” has causal interactions between distinct units in the system. As stated earlier, brain connectivity can be described at three levels. At microlevel, it connects neurons through electrical or chemical synapses. A column of neurons can be considered as a unit in the mesolevel and regions of the brain comprising a large number of neurons and neuron populations as units in the macrolevel. The links in the latter case are the inter-regional pathways, forming large-scale connectivity. 

Figure 2 Types of brain connectivity

 

Figure 2 shows the three types of connectivity. The analysis is done using the directed graphs (see Sporns, O. (2007) and Hilgetag, C. C. (2002)). In the structural brain connectivity type, the connectivity is a sparse and directed graph. The functional brain connectivity has bidirectional graphs. The effective brain connectivity is bidirectional with interactive cause and effect relationships. Another representation of the connectivity is by matrix representation (See Sporns, O. (2007)). Hilgetag, C. C. (2002) describes the computational analysis of brain connectivity.

Modular models of brain function

Arbib, M. A. (2007) describes the modular models as follows. “Modular models of the brain aid the understanding of a complex system by decomposing it into structural modules (e.g., brain regions, layers, columns) or functional modules (schemas) and exploring the patterns of competition and cooperation that yield the overall function.” This definition is not the same as that defined in functional connectivity. The modular approach is intended to build cognitive models and is, in complexity, between the anatomically defined brain regions (defined as macrolevel in brain connectivity) and the computational model at the neuron level.

There are three views of modules for modeling. They are (1) modules for brain structures, (2) modules as schemas, and (3) modules as interfaces. Figure 3 presents the modular design of a model for reflex control of saccades (Arbib, M. A. (2007)). It involves two main modules, one for superior colliculus (SC), and one for brain stem. Each of these is decomposed into sub-modules, with each sub-module defining an array of physiologically defined neurons. In Figure 3(b) the model of Figure 3(a) is embedded into a far larger model which embraces various regions of cerebral cortex (represented by the modules Pre-LIP Vis, Ctx., LIP, PFC, and FEF), thalamus, and basal ganglia. While the model may indeed be analyzed at this top level of modular decomposition, we need to further decompose basal ganglia, BG, as shown in Figure 3(c) if we are to tease apart the role of dopamine in differentially modulating (the 2 arrows shown arising from SNc) the direct and indirect pathways within the basal ganglia (Crowley, M. (1997)). Neural Simulation Language (NSL) has been developed to provide a simulation system for large-scale general neural networks. It provides an environment to develop an object-oriented approach to brain modeling. NSL supports neural models having as basic data structure neural layers with similar properties and similar connection patterns. Models developed using NSL are documented in Brain Operation Database (BODB) as hierarchically organized modules that can be decomposed into lower levels.

Artificial neural networks

As mentioned in Section 2.4, development of artificial neural network (ANN), or neural network as it is now called, started as simulation of biological neuron network and ended up using artificial neurons. Major development work has gone into industrial applications with learning process. Complex problems were addressed by simplifying the assumptions. Algorithms were developed to achieve a neurological related performance, such as learning from experience. Since the background and overview have been covered in the other internal references, the discussion here is limited to the types of models. The models are at the system or network level.

The four main features of an ANN are topology, data flow, types of input values, and forms of activation (Meireles, M. R. G. (2003), Munakata, T. (1998)). Topology can be multilayered, single-layered, or recurrent. Data flow can be recurrent with feedback or non-recurrent with feedforward model. The inputs are binary, bipolar, or continuous. The activation is linear, step, or sigmoid. Multilayer Perceptron (MLP) is the most popular of all the types, which is generally trained with back-propagation of error algorithm. Each neuron output is connected to every neuron in subsequent layers connected in cascade and with no connections between neurons in the same layer. Figure 4 shows a basic MLP topology (Meireles, M. R. G. (2003)), and a basic telecommunication network (Subramanian, M. (2010)) that most are familiar with. We can equate the routers at the nodes in telecommunication network to neurons in MLP technology and the links to synapses.

Figure 4(a) Basic telecommunication network

 

Figure 4(b) Basic MLP technology model Figure 4. Telecommunication network and neural network topologies

Computational neuron models

Computational science is an interdisciplinary field that combines engineering, biology, control systems, brain functions, physical sciences, and computer science. It has fundamental development models done at the lower levels of ions, neurons, and synapses, as well as information propagation between neurons. These models have established the enabling technology for higher-level models to be developed. They are based on chemical and electrical activities in the neurons for which electrical equivalent circuits are generated. A simple model for the neuron with predominantly potassium ions inside the cell and sodium ions outside establishes an electric potential on the membrane under equilibrium, i.e., no external activity, condition. This is called the resting membrane potential, which can be determined by Nernst Equation (Nernst, W. (1888)). An equivalent electrical circuit for a patch of membrane, for example an axon or dendrite, is shown in Figure 5. E_K and E_Na are the potentials associated with the potassium and sodium channels respectively and R_K and R_Na are the resistances associated with them. C is the capacitance of the membrane and I is the source current, which could be the test source or the signal source (action potential). The resting potential for potassium-sodium channels in a neuron is about -65 millivolts.

Figure 5 Membrane model

The membrane model is for a small section of the cell membrane; for larger sections it can be extended by adding similar sections, called compartments, with the parameter values being the same or different. The compartments are cascaded by a resistance, called axial resistance. Figure 6 shows a compartmental model of a neuron that is developed over the membrane model. Dendrites are the postsynaptic receptors receiving inputs from other neurons; and the axon with one or more axon terminals transmits neurotransmitters to other neurons. 

Figure 6 Neuron model

The second building block is the Hodgkin-Huxley (HH) model of the action potential. When the membrane potential from the dendrites exceeds the resting membrane potential, a pulse is generated by the neuron cell and propagated along the axon. This pulse is called the action potential and HH model is a set of equations that is made to fit the experimental data by the design of the model and the choice of the parameter values.

Models for more complex neurons containing other types of ions can be derived by adding to the equivalent circuit additional battery and resistance pairs for each ionic channel. The ionic channel could be passive or active as they could be gated by voltage or be ligands. The extended HH model has been developed to handle the active channel situation.

Although there are neurons that are physiologically connected to each other, information is transmitted at most of the synapses by chemical process across a cleft. Synapses are also computationally modeled. The next level of complexity is that of stream of action potentials, which are generated, whose pattern contains the coding information of the signal being transmitted. There are basically two types of action potentials, or spikes as they are called, that are generated. One is “integrate-and-fire” (the one we have so far addressed) and the other which is rate based. The latter is a stream whose rate varies. The signal going across the synapses could be modeled either as a deterministic or a stochastic process based on the application (See Section 3.7). Another anatomical complication is when a population of neurons, such as a column of neurons in visionary system, needs to be handled. This is done by considering the collective behavior of the group (Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, F. T., & Northoff, G. (2002)).

Spiking neuron models

The action potential or the spike does not itself carry any information. It is the stream of spikes, called spike train, that carry the information in its number and pattern of spikes and timing of spikes. The postsynaptic potential can be either positive, the excitatory synapse or negative, inhibitory synapse. In modeling, the postsynaptic potentials received by the dendrites in the postsynaptic neuron are integrated and when the integrated potential exceeds the resting potential, the neuron fires an action potential along its axon. This model is the Integrate-and-Fire (IF) model that was mentioned in Section 2.3. Closely related to IF model is a model called Spike Response Model (SRM) (Gerstner, W. (1995) Pages 738-758) that is dependent on impulse function response convoluted with the input stimulus signal. This forms a base for a large number of models developed for spiking neural networks. 

The IF and SR model of spike train occurs in Type I neurons, in which the spike rate or spike frequency of the occurrence increases smoothly with the increase in stimulus current starting from zero. Another phenomenon of spike train generation happens in Type II neurons, where firing occurs at the resting potential threshold, but with a quantum jump to a non-zero frequency. Models have been developed using the rate (frequency) of the spike train and are called rate-based models. 

What is important for understanding the functions of the nervous system is how the message is coded and transported by the action potential in the neuron. There are two theories on how the signal that is being propagated is coded in the spikes as to whether it is pulse code or rate code. In the former, it is the time delay of the first spike from the time of stimulus as seen by the postsynaptic receiver that determines the coding. In the rate code, it is average rate of the spike that influences the coding. It is not certain as to which is really the actual physiological phenomenon in each case. However, both cases can be modeled computationally and the parameters varied to match the experimental result. The pulse mode is more complex to model and numerous detailed neuron models and population models are described by Gerstner and Kistler in Parts I and II of Gerstner, W., & Kistler, W. (2002) and Chapter 8 of Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011). Another important characteristic associated with SR model is the spike-time-dependent-plasticity. It is based on Hebb’s postulate on plasticity of synapse, which states that “the neurons that fire together wire together.” This causes the synapse to be a long-term potentiation (LTP) or long-term depression (LTD). The former is the strengthening of the synapse between two neurons if the postsynaptic spike temporally follows immediately after the presynaptic spike. Latter is the case if it is reverse, i.e., the presynaptic spike occurs after the postsynaptic spike. Gerstner, W. & Kistler, W. (2002) in Chapter 10 and Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) in Chapter 7 discuss the various models related to Hebbian models on plasticity and coding.

Nervous system network models

The challenge involved in developing models for small, medium, and large networks is one of reducing the complexity by making valid simplifying assumptions in and extending the Hodgkin-Huxley neuronal model appropriately to design those models ( see Chapter 9 of Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011), Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, F. T., & Northoff, G. (2002), and Chapter 9 of Gerstner, W., & Kistler, W. (2002)). Network models can be classified as either network of neurons propagating through different levels of cortex or neuron populations interconnected as multilevel neurons. The spatial positioning of neuron could be 1-, 2- or 3-dimensional; the latter ones are called small-world networks as they are related to local region. The neuron could be either excitatory or inhibitory, but not both. Modeling design depends on whether it is artificial neuron or biological neuron of neuronal model. Type I or Type II choice needs to be made for the firing mode. Signaling in neurons could be rate-based neurons, spiking response neurons, or deep-brain stimulated. The network can be designed as feedforward or recurrent type. The network needs to be scaled for the computational resource capabilities. Large-scale thalamocortical systems are handled in the manner of the Blue Brain project (Markam, H. (2006)).

Nervous system development models

No generalized modeling concepts exist for modeling the development of anatomical physiology and morphology similar to the one of behavior of neuronal network, which is based on HH model. Shankle, W. R., Hara, J., Fallon, J. H., and Landing, B. H. (2002) describe the application of neuroanatomical data of the developing human cerebral cortex to computational models. Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) discuss aspects of the nervous system of computational modeling in the development of nerve cell morphology, cell physiology, cell patterning, patterns of ocular dominance, and connection between nerve cell and muscle, and retinotopic maps. Carreira-Perpinan, M. A. & Goodhill, G. J. (2002) deal with the optimization of the computerized models of the visual cortex.

Modeling tools

With the enormous number of models that have been created, tools have been developed for dissemination of the information, as well as platforms to develop models. Several generalized tools, such as GENESIS, NEURON, XPP, and NEOSIM are available and are discussed by Hucka, M. (2002).

Lateralization of brain function

From Wikipedia, the free encyclopedia

The human brain is divided into two hemispheres–left and right. Scientists continue to explore how some cognitive functions tend to be dominated by one side or the other; that is, how they are lateralized.

 

The lateralization of brain function is the tendency for some neural functions or cognitive processes to be specialized to one side of the brain or the other. The medial longitudinal fissure separates the human brain into two distinct cerebral hemispheres, connected by the corpus callosum. Although the macrostructure of the two hemispheres appears to be almost identical, different composition of neuronal networks allows for specialized function that is different in each hemisphere. Lateralization of brain structures is based on general trends expressed in healthy patients; however, there are numerous counterexamples to each generalization. Each human's brain develops differently leading to unique lateralization in individuals. This is different from specialization as lateralization refers only to the function of one structure divided between two hemispheres. Specialization is much easier to observe as a trend since it has a stronger anthropological history. The best example of an established lateralization is that of Broca's and Wernicke's areas where both are often found exclusively on the left hemisphere. These areas frequently correspond to handedness, however, meaning that the localization of these areas is regularly found on the hemisphere corresponding to the dominant hand (anatomically on the opposite side). Function lateralization such as semantics, intonation, accentuation, prosody, etc. has since been called into question and largely been found to have a neuronal basis in both hemispheres. Another example is that each hemisphere in the brain tends to represent one side of the body. In the cerebellum this is the same bodyside, but in the forebrain this is predominantly the contralateral side.

Lateralized functions

Language

Language functions such as grammar, vocabulary and literal meaning are typically lateralized to the left hemisphere, especially in right handed individuals. While language production is left-lateralized in up to 90% of right-handers, it is more bilateral, or even right-lateralized, in approximately 50% of left-handers.

Broca's area and Wernicke's area, two areas associated with the production of speech, are located in the left cerebral hemisphere for about 95% of right-handers, but about 70% of left-handers.

Auditory and visual processing

The processing of visual and auditory stimuli, spatial manipulation, facial perception, and artistic ability are represented bilaterally. Numerical estimation, comparison and online calculation depend on bilateral parietal regions while exact calculation and fact retrieval are associated with left parietal regions, perhaps due to their ties to linguistic processing.

Clinical significance

Depression is linked with a hyperactive right hemisphere, with evidence of selective involvement in "processing negative emotions, pessimistic thoughts and unconstructive thinking styles", as well as vigilance, arousal and self-reflection, and a relatively hypoactive left hemisphere, "specifically involved in processing pleasurable experiences" and "relatively more involved in decision-making processes". Additionally, "left hemisphere lesions result in an omissive response bias or error pattern whereas right hemisphere lesions result in a commissive response bias or error pattern." The delusional misidentification syndromes, reduplicative paramnesia and Capgras delusion are also often the result of right hemisphere lesions.

Hemisphere damage

Damage to either the right or left hemisphere, and its resulting deficits provide insight into the function of the damaged area. Left hemisphere damage has many effects on language production and perception. Damage or lesions to the right hemisphere can result in a lack of emotional prosody or intonation when speaking. Right hemisphere damage also has grave effects on understanding discourse. People with damage to the right hemisphere have a reduced ability to generate inferences, comprehend and produce main concepts, and a reduced ability to manage alternative meanings. Furthermore, people with right hemisphere damage often exhibit discourse that is abrupt and perfunctory or verbose and excessive. They can also have pragmatic deficits in situations of turn taking, topic maintenance and shared knowledge. 

Lateral brain damage can also affect visual perceptual spatial resolution. People with left hemisphere damage may have impaired perception of high resolution, or detailed, aspects of an image. People with right hemisphere damage may have impaired perception of low resolution, or big picture, aspects of an image.

Plasticity

If a specific region of the brain, or even an entire hemisphere, is injured or destroyed, its functions can sometimes be assumed by a neighboring region in the same hemisphere or the corresponding region in the other hemisphere, depending upon the area damaged and the patient's age. When injury interferes with pathways from one area to another, alternative (indirect) connections may develop to communicate information with detached areas, despite the inefficiencies.

Broca's aphasia

Broca's aphasia is a specific type of expressive aphasia and is so named due to the aphasia that results from damage or lesions to the Broca's area of the brain, that exists most commonly in the left inferior frontal hemisphere. Thus, the aphasia that develops from the lack of functioning of the Broca's area is an expressive and non-fluent aphasia. It is called 'non-fluent' due the issues that arise because Broca's area is critical for language pronunciation and production. The area controls some motor aspects of speech production and articulation of thoughts to words and as such lesions to the area result in the specific non-fluent aphasia.

Wernicke's aphasia

Wernicke's aphasia is the result of damage to the area of the brain that is commonly in the left hemisphere above the sylvian fissure. Damage to this area causes primarily a deficit in language comprehension. While the ability to speak fluently with normal melodic intonation is spared, the language produced by a person with Wernicke's aphasia is riddled with semantic errors, and may sound nonsensical to the listener. Wernicke's aphasia is characterized by phonemic paraphasias, neologism or jargon. Another characteristic of a person with Wernicke's aphasia is that they are unconcerned by the mistakes that they are making.

Society and culture

Misapplication

Terence Hines states that the research on brain lateralization is valid as a research program, though commercial promoters have applied it to promote subjects and products far outside the implications of the research. For example, the implications of the research have no bearing on psychological interventions such as EMDR and neurolinguistic programming, brain-training equipment, or management training.

Pop psychology

The oversimplification of lateralization in pop psychology. This belief was widely held even in the scientific community for some years.

 

Some popularizations oversimplify the science about lateralization, by presenting the functional differences between hemispheres as being more absolute than is actually the case.

Sex differences

In the 19th century and to a lesser extent the 20th, it was thought that each side of the brain was associated with a specific gender: the left corresponding with masculinity and the right with femininity and each half could function independently. The right side of the brain was seen as the inferior and thought to be prominent in women, savages, children, criminals, and the insane. A prime example of this in fictional literature can be seen in Robert Louis Stevenson's Strange Case of Dr. Jekyll and Mr. Hyde.

Evolutionary advantage

The widespread lateralization of many vertebrate animals indicates an evolutionary advantage associated with the specialization of each hemisphere.

History

Broca

One of the first indications of brain function lateralization resulted from the research of French physician Pierre Paul Broca, in 1861. His research involved the male patient nicknamed "Tan", who suffered a speech deficit (aphasia); "tan" was one of the few words he could articulate, hence his nickname. In Tan's autopsy, Broca determined he had a syphilitic lesion in the left cerebral hemisphere. This left frontal lobe brain area (Broca's area) is an important speech production region. The motor aspects of speech production deficits caused by damage to Broca's area are known as expressive aphasia. In clinical assessment of this aphasia, it is noted that the patient cannot clearly articulate the language being employed.

Wernicke

German physician Karl Wernicke continued in the vein of Broca's research by studying language deficits unlike expressive aphasia. Wernicke noted that not every deficit was in speech production; some were linguistic. He found that damage to the left posterior, superior temporal gyrus (Wernicke's area) caused language comprehension deficits rather than speech production deficits, a syndrome known as receptive aphasia.

Imaging

These seminal works on hemispheric specialization were done on patients or postmortem brains, raising questions about the potential impact of pathology on the research findings. New methods permit the in vivo comparison of the hemispheres in healthy subjects. Particularly, magnetic resonance imaging (MRI) and positron emission tomography (PET) are important because of their high spatial resolution and ability to image subcortical brain structures.

Movement and sensation

In the 1940s, neurosurgeon Wilder Penfield and his neurologist colleague Herbert Jasper developed a technique of brain mapping to help reduce side effects caused by surgery to treat epilepsy. They stimulated motor and somatosensory cortices of the brain with small electrical currents to activate discrete brain regions. They found that stimulation of one hemisphere's motor cortex produces muscle contraction on the opposite side of the body. Furthermore, the functional map of the motor and sensory cortices is fairly consistent from person to person; Penfield and Jasper's famous pictures of the motor and sensory homunculi were the result.

Split-brain patients

Research by Michael Gazzaniga and Roger Wolcott Sperry in the 1960s on split-brain patients led to an even greater understanding of functional laterality. Split-brain patients are patients who have undergone corpus callosotomy (usually as a treatment for severe epilepsy), a severing of a large part of the corpus callosum. The corpus callosum connects the two hemispheres of the brain and allows them to communicate. When these connections are cut, the two halves of the brain have a reduced capacity to communicate with each other. This led to many interesting behavioral phenomena that allowed Gazzaniga and Sperry to study the contributions of each hemisphere to various cognitive and perceptual processes. One of their main findings was that the right hemisphere was capable of rudimentary language processing, but often has no lexical or grammatical abilities. Eran Zaidel also studied such patients and found some evidence for the right hemisphere having at least some syntactic ability. 

Language is primarily localized in the left hemisphere. One of the experiments carried out by Gazzaniga involved a split-brain male patient sitting in front of a computer screen while having words and images presented on either side of the screen and the visual stimuli would go to either the right or left visual field, and thus the left or right brain, respectively. It was observed that if the patient was presented with an image to his left visual field (right brain), he would report not seeing anything. If he was able to feel around for certain objects, he could accurately pick out the correct object, despite not having the ability to verbalize what he saw. This led to confirmation that the left brain is localized for language whereas the right brain does not have this capability, and when the corpus callosum is cut, the two hemispheres cannot communicate in order for situation-pertinent speech to be produced.

Additional images

• 

  Ventricles of brain and basal ganglia. Superior view. Horizontal section. Deep dissection
  
• 

  Ventricles of brain and basal ganglia. Superior view. Horizontal section. Deep dissection