Schematic illustrating the r-process as it occurs in supernovae or neutron star collisions. Neutrons are rapidly absorbed faster than the resulting nuclei can beta-decay; this allows the r-process to produce very neutron-rich nuclei follow the neutron drip line. There are waiting points located at magic numbers N
= 50, 82, 126, where beta-decay is favored due to low neutron-capture
cross sections resulting from the closed shells. The cycle then repeats
until the next waiting point, creating yet heavier nuclei of elements up
to the actinides; the natural abundance of these elements results entirely from the r-process. In the superheavy mass region (A ≥ 270), neutron-induced fission or spontaneous fission are expected to become dominant and end the r-process. Most nuclei along the hypothetical r-process path, however, are unknown.
The rapid neutron-capture process, or so-called r-process, is a set of nuclear reactions that in nuclear astrophysics is responsible for the creation (nucleosynthesis) of approximately half the abundances of the atomic nuclei heavier than iron,
usually synthesizing the entire abundance of the two most neutron-rich
stable isotopes of each heavy element. Chemical elements heavier than
iron typically are enabled by the force between nucleons to be capable
of six to ten stable isotopic forms having the same nuclear charge Z but
differing in neutron number N, each of whose natural abundances
contribute to the natural abundance of the chemical element. Each
isotope is characterized by the number of neutrons that it contains. The r-process
typically synthesizes new nuclei of the heaviest four isotopes of any
heavy element, being totally responsible for the abundances of its two
heaviest isotopes, which are referred to as r-only nuclei. The most abundant of these contribute to the r-process abundance peaks near atomic weights A = 82 (elements Se, Br and Kr), A = 130 (elements Te, I, and Xe) and A = 196 (elements Os, Ir and Pt).
The r-process entails a succession of rapid neutron captures (hence the name) by one or more heavy seed nuclei, typically beginning with nuclei in the abundance peak centered on 56Fe. The captures must be rapid in the sense that the nuclei must not have time to undergo radioactive decay before another neutron
arrives to be captured, a sequence that is halted only when the
increasingly neutron-rich nuclei cannot physically retain another
neutron. The r-process therefore must occur in locations where there exists a high density of free neutrons. Early studies reasoned that 1024 free neutrons per cm3
would be required if the temperature were about one billion degrees in
order that the waiting points, at which no more neutrons can be
captured, be at the atomic numbers of the abundance peaks for r-process nuclei.
This amounts to almost a gram of free neutrons in every cubic
centimeter, an astonishing number requiring extreme locations.
Traditionally this suggested the material ejected from the reexpanded
core of a core-collapse supernova (as part of supernova nucleosynthesis) or decompression of neutron-star matter thrown off by a binary neutron star merger. The relative contributions of these sources to the astrophysical abundance of r-process elements is a matter of ongoing research.
A limited r-process-like series of neutron captures occurs to a minor extent in thermonuclear weapon explosions. These led to the discovery of the elements einsteinium (element 99) and fermium (element 100) in nuclear weapon fallout.
The r-process contrasts with the s-process, the other predominant mechanism for the production of heavy elements, which is nucleosynthesis by means of slow captures of neutrons. The s-process primarily occurs within ordinary stars, particularly AGB stars, where the neutron flux is sufficient to cause neutron captures to recur every 10–100 years, much too slow for the r-process, which requires 100 captures per second. The s-process is secondary,
meaning that it requires pre-existing heavy isotopes as seed nuclei to
be converted into other heavy nuclei by a slow sequence of captures of
free neutrons. The r-process scenarios create their own seed
nuclei, so they might proceed in massive stars that contain no heavy
seed nuclei. Taken together, the r- and s-processes account for almost the entire abundance of chemical elements heavier than iron. The historical challenge has been to locate physical settings appropriate for their time scales.
History
The
need for a physical setting providing rapid capture of neutrons was seen
from the relative abundances of isotopes of heavy chemical elements
given in a table of abundances by Hans Suess and Harold Urey in 1956. Not only did their abundance table reveal larger than average abundances of natural isotopes containing magic numbers of neutrons but also abundance peaks about 10 amu
lighter than those containing magic numbers of neutrons in their
structure. They also realized that captures of free neutrons should be
part of any explanation because of the lack of electric repulsion
between nuclei and chargeless neutrons. This phenomenology suggested
that these lighter subsidiary abundance peaks could result from
radioactive nuclei having the magic neutron numbers but roughly ten
fewer protons. To achieve this would require radioactive neutron-rich
isotopes to capture another neutron faster than they can undergo beta
decay in order to create abundance peaks that will decay subsequently to
germanium, xenon, and platinum, elements prominent in the r-process abundance peaks. According to the nuclear shell model, radioactive nuclei that would decay into isotopes of these elements must have closed neutron shells near the neutron drip line, where more neutrons cannot be added. The neutron-capture flow must therefore wait for beta decay at those so-called waiting points,
which therefore grow larger in abundance similar to water in a dammed
up river. For those hitherto unexplained abundance peaks, which are
approximately 10 u lighter than the s-process abundance peaks, to be created by rapid neutron capture
implied that other neutron-rich nuclei would also be synthesized by the
same process. That process, rapid neutron capture by neutron-rich
isotopes, is called the r-process. A table apportioning the heavy isotopes phenomenologically between s-process and r-process isotopes was published in 1957 in the famous B2FH review paper which named the r-process and outlined the physics that guides it. Alastair G. W. Cameron also published a smaller study about the r-process in the same year.
The stationary r-process as described by the B2FH paper was first demonstrated in a time-dependent calculation at Caltech by Phillip A. Seeger, William A. Fowler and Donald D. Clayton, who found that no single temporal snapshot matched the solar r-process abundances, but, that when superposed, did achieve a successful characterization of the r-process abundance distribution. Shorter-time distributions emphasize abundances at atomic weights less than A = 140, whereas longer-time distributions emphasized those at atomic weights greater than A = 140. Subsequent treatments of the r-process reinforced those temporal features. Seeger et al. were also able to construct more quantitative apportionment between s-process and r-process of the abundance table of heavy isotopes, thereby establishing a more reliable abundance curve for the r-process isotopes than B2FH had been able to define. Today, the r-process abundances are determined using their technique of subtracting the more reliable s-process isotopic abundances from the total isotopic abundances and attributing the remainder to r-process nucleosynthesis. That r-process
abundance curve (vs. atomic weight) has provided for many decades the
target for theoretical computations of abundances synthesized by the
physical r-process.
The creation of free neutrons by electron capture during the
rapid collapse to high density of a supernova core along with quick
assembly of some neutron-rich seed nuclei makes the r process a primary nucleosynthesis process, meaning a process that can occur even in a star initially of pure H and He, in contrast to the B2FH designation as a secondary process
building on preexisting iron. Primary stellar nucleosynthesis begins
earlier in the galaxy than does secondary nucleosynthesis. Alternatively
the high density of neutrons within neutron stars would be available
for rapid assembly into r-process nuclei if a collision were to
eject portions of a neutron star, which then rapidly expands freed from
confinement. That sequence could also begin earlier in galactic time
than would s-process nucleosynthesis; so each scenario fits the earlier growth of r-process abundances in the galaxy. Each of these scenarios is the subject of active theoretical research.
Observational evidence of the early r-process enrichment of
interstellar gas and of subsequent newly formed of stars, as applied to
the abundance evolution of the galaxy of stars, was first laid out by
James W. Truran in 1981.
He and subsequent astronomers showed that the pattern of heavy-element
abundances in the earliest metal-poor stars matched that of the shape of
the solar r-process curve, as if the s-process component were missing. This was consistent with the hypothesis that the s-process had not yet begun to enrich interstellar gas when these young stars missing the s-process abundances were born from that gas, for it requires about 100 million years of galactic history for the s-process to get started whereas the r process can begin after two million years. These s-process-poor, r-process-rich stellar compositions must have been born earlier than any s-process, showing that the r-process
emerges from quickly-evolving massive stars that become supernovae and
leave neutron-star remnants that can merge with another neutron star.
The primary nature of the early r-process thereby derives from observed abundance spectra in old stars that had been born early, when the galactic metallicity was still small, but that nonetheless contain their complement of r-process nuclei.
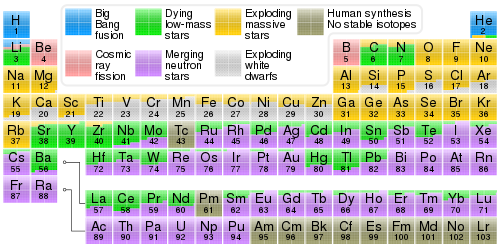
Periodic table
showing the cosmogenic origin of each element. The elements heavier
than iron with origins in supernovae are typically those produced by the
r-process, which is powered by supernovae neutron bursts
Either interpretation, though generally supported by supernova
experts, has yet to achieve a totally satisfactory calculation of r-process
abundances because the overall problem is numerically formidable; but
existing results are supportive. And in 2017 new data about the r-process
was discovered when the LIGO and Virgo gravitational-wave observatories
discovered a merger of two neutron stars ejecting r-process matter.
Noteworthy is that the r-process is responsible for our
natural cohort of radioactive elements, such as uranium and thorium, as
well as the most neutron-rich isotopes of each heavy element.
Nuclear physics
Immediately after the severe compression of electrons in a core-collapse supernova, beta-minus decay is blocked. This is because the high electron density fills all available free electron states up to a Fermi energy which is greater than the energy of nuclear beta decay. But nuclear capture of those free electrons still occurs, and causes increasing neutronization
of matter. There results an extremely high density of free neutrons
which cannot decay, and as a result a large neutron density (on the
order of 1024 neutrons per cm3) and high temperatures. As this re-expands and cools, neutron capture by still-existing heavy nuclei occurs much faster than beta-minus decay. As a consequence, the r-process runs up along the neutron drip line and highly-unstable neutron-rich nuclei are created.
Three processes which affect the process of climbing the neutron drip line are; a notable decrease in the neutron-capture cross section at nuclei with closed neutron shells, the inhibiting process of photodisintegration, and the degree of nuclear stability in the heavy-isotope region. This last phenomenon terminates the r-process
when its heaviest nuclei become unstable to spontaneous fission, which
is currently believed to be in the neutron-rich region of the table of nuclides
when the total number of nucleons approaches 270; even before this, the
fission barrier may be low enough that neutron capture might induce
fission instead of continuing up the neutron drip line. After the neutron flux decreases, these highly unstable radioactive nuclei undergo a rapid succession of beta decays until they reach more stable, neutron-rich nuclei. So, while the s-process creates an abundance of stable nuclei having closed neutron shells, the r-process in neutron-rich predecessor nuclei creates an abundance of radioactive nuclei about 10 amu below the s-process peaks after their decay back to stability.
The r-process also occurs in thermonuclear weapons, and
was responsible for the initial discovery of neutron-rich almost stable
isotopes of actinides like plutonium-244 and the new elements einsteinium and fermium
(atomic numbers 99 and 100) in the 1950s. It has been suggested that
multiple nuclear explosions would make it possible to reach the island of stability,
as the affected nuclides (starting with uranium-238 as seed nuclei)
would not have time to beta decay all the way to the quickly
spontaneously fissioning nuclides at the line of beta stability before
they absorbed more neutrons in the next explosion, thus providing a
chance to reach neutron-rich superheavy nuclides like copernicium-291 and -293 which should have half-lives of centuries or millennia.
Astrophysical sites
The most probable candidate site for the r-process has long been suggested to be core-collapse supernovae (spectral types Ib, Ic and II), which may provide the necessary physical conditions for the r-process. However, the very low abundance of r-process nuclei
in the interstellar gas limits the amount each can have ejected. It
requires either that only a small fraction of supernovae eject r-process nuclei to the interstellar medium, or that each supernova ejects only a very small amount of r-process
material. The ejected material must be relatively neutron-rich, a
condition which has been difficult to achieve in models, so that astrophysicists remain uneasy about their adequacy for successful r-process yields.
Entirely new astronomical data about the r process was
discovered in 2017 when the LIGO and Virgo gravitational-wave
observatories discovered a merger of two neutron stars.
The localization on the sky of the source of the gravitational waves
radiated by the collapse of the two neutron stars into a black hole, but
with significant spun off mass of highly neutronized matter, enabled
several teams to discover and study the optical counterpart of the merger, finding spectroscopic evidence of r-process
material thrown off by the merging neutron stars. The bulk of this
material seems to consist of two types: hot blue masses of highly
radioactive r-process matter of lower-mass-range heavy nuclei (A < 140) and cooler red masses of higher mass-number r-process nuclei (A > 140)
rich in actinides (such as uranium, thorium, californium etc). When
released from the huge internal pressure of the neutron star, these
ejecta expand and form seed heavy nuclei that rapidly capture free
neutrons, and radiate detected optical light for about a week. Such
duration of luminosity would not be possible without heating by internal
radioactive decay, which is provided by r-process nuclei near their waiting points. Two distinct mass regions (A < 140 and A > 140) for the r-process yields have been known since the first time dependent calculations of the r-process.
Because of these spectroscopic features it has been argued that such
nucleosynthesis in the Milky Way has been primarily ejecta from
neutron-star mergers rather than from supernovae.
These results offer a new possibility for clarifying six decades of uncertainty over the site of origin of r-process nuclei. Confirming relevance to the r-process is that it is radiogenic power from radioactive decay of r-process nuclei that maintains the visibility of these spun off r-process fragments. Otherwise they would dim quickly. Such alternative sites were first seriously proposed in 1974 as decompressing neutron star matter. It was proposed such matter is ejected from neutron stars merging with black holes in compact binaries. In 1989 (and 1999) this scenario was extended to binary neutron star mergers (a binary star system of two neutron stars that collide). After preliminary identification of these sites, the scenario was confirmed in GW170817.