Non-Euclidean geometry

From Wikipedia, the free encyclopedia

Behavior of lines with a common perpendicular in each of the three types of geometry

In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those specifying Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises when either the metric requirement is relaxed, or the parallel postulate is replaced with an alternative one. In the latter case one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras which give rise to kinematic geometries that have also been called non-Euclidean geometry.

The essential difference between the metric geometries is the nature of parallel lines. Euclid's fifth postulate, the parallel postulate, is equivalent to Playfair's postulate, which states that, within a two-dimensional plane, for any given line ℓ and a point A, which is not on ℓ, there is exactly one line through A that does not intersect ℓ. In hyperbolic geometry, by contrast, there are infinitely many lines through A not intersecting ℓ, while in elliptic geometry, any line through A intersects ℓ.

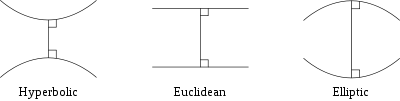
Another way to describe the differences between these geometries is to consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular to a third line:

• In Euclidean geometry, the lines remain at a constant distance from each other (meaning that a line drawn perpendicular to one line at any point will intersect the other line and the length of the line segment joining the points of intersection remains constant) and are known as parallels.
• In hyperbolic geometry, they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels.
• In elliptic geometry, the lines "curve toward" each other and intersect.

History

Background

Euclidean geometry, named after the Greek mathematician Euclid, includes some of the oldest known mathematics, and geometries that deviated from this were not widely accepted as legitimate until the 19th century.

The debate that eventually led to the discovery of the non-Euclidean geometries began almost as soon as Euclid's work Elements was written. In the Elements, Euclid began with a limited number of assumptions (23 definitions, five common notions, and five postulates) and sought to prove all the other results (propositions) in the work. The most notorious of the postulates is often referred to as "Euclid's Fifth Postulate," or simply the "parallel postulate", which in Euclid's original formulation is:

If a straight line falls on two straight lines in such a manner that the interior angles on the same side are together less than two right angles, then the straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

Other mathematicians have devised simpler forms of this property. Regardless of the form of the postulate, however, it consistently appears to be more complicated than Euclid's other postulates:

1. To draw a straight line from any point to any point.
2. To produce [extend] a finite straight line continuously in a straight line.
3. To describe a circle with any centre and distance [radius].
4. That all right angles are equal to one another.

For at least a thousand years, geometers were troubled by the disparate complexity of the fifth postulate, and believed it could be proved as a theorem from the other four. Many attempted to find a proof by contradiction, including Ibn al-Haytham (Alhazen, 11th century),^[1] Omar Khayyám (12th century), Nasīr al-Dīn al-Tūsī (13th century), and Giovanni Girolamo Saccheri (18th century).

The theorems of Ibn al-Haytham, Khayyam and al-Tusi on quadrilaterals, including the Lambert quadrilateral and Saccheri quadrilateral, were "the first few theorems of the hyperbolic and the elliptic geometries." These theorems along with their alternative postulates, such as Playfair's axiom, played an important role in the later development of non-Euclidean geometry. These early attempts at challenging the fifth postulate had a considerable influence on its development among later European geometers, including Witelo, Levi ben Gerson, Alfonso, John Wallis and Saccheri.^[2] All of these early attempts made at trying to formulate non-Euclidean geometry however provided flawed proofs of the parallel postulate, containing assumptions that were essentially equivalent to the parallel postulate. These early attempts did, however, provide some early properties of the hyperbolic and elliptic geometries.

Khayyam, for example, tried to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle): "Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge."^[3] Khayyam then considered the three cases right, obtuse, and acute that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he correctly refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid which he didn't realize was equivalent to his own postulate. Another example is al-Tusi's son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), who wrote a book on the subject in 1298, based on al-Tusi's later thoughts, which presented another hypothesis equivalent to the parallel postulate. "He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the Elements."^[4][5] His work was published in Rome in 1594 and was studied by European geometers, including Saccheri^[4] who criticised this work as well as that of Wallis.^[6]

Giordano Vitale, in his book Euclide restituo (1680, 1686), used the Saccheri quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant.

In a work titled Euclides ab Omni Naevo Vindicatus (Euclid Freed from All Flaws), published in 1733, Saccheri quickly discarded elliptic geometry as a possibility (some others of Euclid's axioms must be modified for elliptic geometry to work) and set to work proving a great number of results in hyperbolic geometry.

He finally reached a point where he believed that his results demonstrated the impossibility of hyperbolic geometry. His claim seems to have been based on Euclidean presuppositions, because no logical contradiction was present. In this attempt to prove Euclidean geometry he instead unintentionally discovered a new viable geometry, but did not realize it.

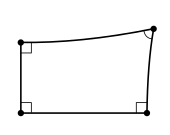
In 1766 Johann Lambert wrote, but did not publish, Theorie der Parallellinien in which he attempted, as Saccheri did, to prove the fifth postulate. He worked with a figure that today we call a Lambert quadrilateral, a quadrilateral with three right angles (can be considered half of a Saccheri quadrilateral). He quickly eliminated the possibility that the fourth angle is obtuse, as had Saccheri and Khayyam, and then proceeded to prove many theorems under the assumption of an acute angle. Unlike Saccheri, he never felt that he had reached a contradiction with this assumption. He had proved the non-Euclidean result that the sum of the angles in a triangle increases as the area of the triangle decreases, and this led him to speculate on the possibility of a model of the acute case on a sphere of imaginary radius. He did not carry this idea any further.^[7]

At this time it was widely believed that the universe worked according to the principles of Euclidean geometry.^[8]

Discovery of non-Euclidean geometry

The beginning of the 19th century would finally witness decisive steps in the creation of non-Euclidean geometry. Circa 1813, Carl Friedrich Gauss and independently around 1818, the German professor of law Ferdinand Karl Schweikart^[9] had the germinal ideas of non-Euclidean geometry worked out, but neither published any results. Then, around 1830, the Hungarian mathematician János Bolyai and the Russian mathematician Nikolai Ivanovich Lobachevsky separately published treatises on hyperbolic geometry. Consequently, hyperbolic geometry is called Bolyai-Lobachevskian geometry, as both mathematicians, independent of each other, are the basic authors of non-Euclidean geometry. Gauss mentioned to Bolyai's father, when shown the younger Bolyai's work, that he had developed such a geometry several years before,^[10] though he did not publish. While Lobachevsky created a non-Euclidean geometry by negating the parallel postulate, Bolyai worked out a geometry where both the Euclidean and the hyperbolic geometry are possible depending on a parameter k. Bolyai ends his work by mentioning that it is not possible to decide through mathematical reasoning alone if the geometry of the physical universe is Euclidean or non-Euclidean; this is a task for the physical sciences.

Bernhard Riemann, in a famous lecture in 1854, founded the field of Riemannian geometry, discussing in particular the ideas now called manifolds, Riemannian metric, and curvature. He constructed an infinite family of geometries which are not Euclidean by giving a formula for a family of Riemannian metrics on the unit ball in Euclidean space. The simplest of these is called elliptic geometry and it is considered to be a non-Euclidean geometry due to its lack of parallel lines.^[11]

By formulating the geometry in terms of a curvature tensor, Riemann allowed non-Euclidean geometry to be applied to higher dimensions.

Terminology

It was Gauss who coined the term "non-Euclidean geometry".^[12] He was referring to his own work which today we call hyperbolic geometry. Several modern authors still consider "non-Euclidean geometry" and "hyperbolic geometry" to be synonyms.

Arthur Cayley noted that distance between points inside a conic could be defined in terms of logarithm and the projective cross-ratio function. The method has become called the Cayley-Klein metric because Felix Klein exploited it to describe the non-euclidean geometries in articles^[13] in 1871 and 73 and later in book form. The Cayley-Klein metrics provided working models of hyperbolic and elliptic metric geometries, as well as Euclidean geometry.

Klein is responsible for the terms "hyperbolic" and "elliptic" (in his system he called Euclidean geometry "parabolic", a term which generally fell out of use^[14]). His influence has led to the current usage of the term "non-Euclidean geometry" to mean either "hyperbolic" or "elliptic" geometry.

There are some mathematicians who would extend the list of geometries that should be called "non-Euclidean" in various ways.^[15]

Axiomatic basis of non-Euclidean geometry

Euclidean geometry can be axiomatically described in several ways. Unfortunately, Euclid's original system of five postulates (axioms) is not one of these as his proofs relied on several unstated assumptions which should also have been taken as axioms. Hilbert's system consisting of 20 axioms^[16] most closely follows the approach of Euclid and provides the justification for all of Euclid's proofs. Other systems, using different sets of undefined terms obtain the same geometry by different paths. In all approaches, however, there is an axiom which is logically equivalent to Euclid's fifth postulate, the parallel postulate. Hilbert uses the Playfair axiom form, while Birkhoff, for instance, uses the axiom which says that "there exists a pair of similar but not congruent triangles." In any of these systems, removal of the one axiom which is equivalent to the parallel postulate, in whatever form it takes, and leaving all the other axioms intact, produces absolute geometry. As the first 28 propositions of Euclid (in The Elements) do not require the use of the parallel postulate or anything equivalent to it, they are all true statements in absolute geometry.^[17]

To obtain a non-Euclidean geometry, the parallel postulate (or its equivalent) must be replaced by its negation. Negating the Playfair's axiom form, since it is a compound statement (... there exists one and only one ...), can be done in two ways:

• Either there will exist more than one line through the point parallel to the given line or there will exist no lines through the point parallel to the given line. In the first case, replacing the parallel postulate (or its equivalent) with the statement "In a plane, given a point P and a line ℓ not passing through P, there exist two lines through P which do not meet ℓ" and keeping all the other axioms, yields hyperbolic geometry.^[18]
• The second case is not dealt with as easily. Simply replacing the parallel postulate with the statement, "In a plane, given a point P and a line ℓ not passing through P, all the lines through P meet ℓ", does not give a consistent set of axioms. This follows since parallel lines exist in absolute geometry,^[19] but this statement says that there are no parallel lines. This problem was known (in a different guise) to Khayyam, Saccheri and Lambert and was the basis for their rejecting what was known as the "obtuse angle case". In order to obtain a consistent set of axioms which includes this axiom about having no parallel lines, some of the other axioms must be tweaked. The adjustments to be made depend upon the axiom system being used. Among others these tweaks will have the effect of modifying Euclid's second postulate from the statement that line segments can be extended indefinitely to the statement that lines are unbounded. Riemann's elliptic geometry emerges as the most natural geometry satisfying this axiom.

Models of non-Euclidean geometry

On a sphere, the sum of the angles of a triangle is not equal to 180°. The surface of a sphere is not a Euclidean space, but locally the laws of the Euclidean geometry are good approximations. In a small triangle on the face of the earth, the sum of the angles is very nearly 180°.

Two dimensional Euclidean geometry is modelled by our notion of a "flat plane."

Elliptic geometry

The simplest model for elliptic geometry is a sphere, where lines are "great circles" (such as the equator or the meridians on a globe), and points opposite each other (called antipodal points) are identified (considered to be the same). This is also one of the standard models of the real projective plane. The difference is that as a model of elliptic geometry a metric is introduced permitting the measurement of lengths and angles, while as a model of the projective plane there is no such metric.In the elliptic model, for any given line ℓ and a point A, which is not on ℓ, all lines through A will intersect ℓ.

Hyperbolic geometry

Even after the work of Lobachevsky, Gauss, and Bolyai, the question remained: "Does such a model exist for hyperbolic geometry?". The model for hyperbolic geometry was answered by Eugenio Beltrami, in 1868, who first showed that a surface called the pseudosphere has the appropriate curvature to model a portion of hyperbolic space and in a second paper in the same year, defined the Klein model which models the entirety of hyperbolic space, and used this to show that Euclidean geometry and hyperbolic geometry were equiconsistent so that hyperbolic geometry was logically consistent if and only if Euclidean geometry was. (The reverse implication follows from the horosphere model of Euclidean geometry.)
In the hyperbolic model, within a two-dimensional plane, for any given line ℓ and a point A, which is not on ℓ, there are infinitely many lines through A that do not intersect ℓ.

In these models the concepts of non-Euclidean geometries are being represented by Euclidean objects in a Euclidean setting. This introduces a perceptual distortion wherein the straight lines of the non-Euclidean geometry are being represented by Euclidean curves which visually bend. This "bending" is not a property of the non-Euclidean lines, only an artifice of the way they are being represented.

Three-dimensional non-Euclidean geometry

In three dimensions, there are eight models of geometries.^[20] There are Euclidean, elliptic, and hyperbolic geometries, as in the two-dimensional case; mixed geometries that are partially Euclidean and partially hyperbolic or spherical; twisted versions of the mixed geometries; and one unusual geometry that is completely anisotropic (i.e. every direction behaves differently).

Uncommon properties

Lambert quadrilateral in hyperbolic geometry

Saccheri quadrilaterals in the three geometries

Euclidean and non-Euclidean geometries naturally have many similar properties, namely those which do not depend upon the nature of parallelism. This commonality is the subject of absolute geometry (also called neutral geometry). However, the properties which distinguish one geometry from the others are the ones which have historically received the most attention.

Besides the behavior of lines with respect to a common perpendicular, mentioned in the introduction, we also have the following:

• A Lambert quadrilateral is a quadrilateral which has three right angles. The fourth angle of a Lambert quadrilateral is acute if the geometry is hyperbolic, a right angle if the geometry is Euclidean or obtuse if the geometry is elliptic. Consequently, rectangles exist (a statement equivalent to the parallel postulate) only in Euclidean geometry.
• A Saccheri quadrilateral is a quadrilateral which has two sides of equal length, both perpendicular to a side called the base. The other two angles of a Saccheri quadrilateral are called the summit angles and they have equal measure. The summit angles of a Saccheri quadrilateral are acute if the geometry is hyperbolic, right angles if the geometry is Euclidean and obtuse angles if the geometry is elliptic.
• The sum of the measures of the angles of any triangle is less than 180° if the geometry is hyperbolic, equal to 180° if the geometry is Euclidean, and greater than 180° if the geometry is elliptic. The defect of a triangle is the numerical value (180° - sum of the measures of the angles of the triangle). This result may also be stated as: the defect of triangles in hyperbolic geometry is positive, the defect of triangles in Euclidean geometry is zero, and the defect of triangles in elliptic geometry is negative.

Importance

Before the models of a non-Euclidean plane were presented by Beltrami, Klein, and Poincaré, Euclidean geometry stood unchallenged as the mathematical model of space. Furthermore, since the substance of the subject in synthetic geometry was a chief exhibit of rationality, the Euclidean point of view represented absolute authority.

The discovery of the non-Euclidean geometries had a ripple effect which went far beyond the boundaries of mathematics and science. The philosopher Immanuel Kant's treatment of human knowledge had a special role for geometry. It was his prime example of synthetic a priori knowledge; not derived from the senses nor deduced through logic — our knowledge of space was a truth that we were born with. Unfortunately for Kant, his concept of this unalterably true geometry was Euclidean. Theology was also affected by the change from absolute truth to relative truth in the way that mathematics is related to the world around it, that was a result of this paradigm shift.^[21]

Non-Euclidean geometry is an example of a scientific revolution in the history of science, in which mathematicians and scientists changed the way they viewed their subjects.^[22] Some geometers called Lobachevsky the "Copernicus of Geometry" due to the revolutionary character of his work.^[23][24]
The existence of non-Euclidean geometries impacted the intellectual life of Victorian England in many ways^[25] and in particular was one of the leading factors that caused a re-examination of the teaching of geometry based on Euclid's Elements. This curriculum issue was hotly debated at the time and was even the subject of a book, Euclid and his Modern Rivals, written by Charles Lutwidge Dodgson (1832–1898) better known as Lewis Carroll, the author of Alice in Wonderland.

Planar algebras

In analytic geometry a plane is described with Cartesian coordinates : C = { (x,y) : x, y ∈ ℝ }. The points are sometimes identified with complex numbers z = x + y ε where ε² ∈ { –1, 0, 1}.

The Euclidean plane corresponds to the case ε² = −1 since the modulus of z is given by

${\displaystyle zz^{\ast }=(x+y\epsilon )(x-y\epsilon )=x^{2}+y^{2}}$

and this quantity is the square of the Euclidean distance between z and the origin. For instance, {z | z z* = 1} is the unit circle.

For planar algebra, non-Euclidean geometry arises in the other cases. When ε² = +1, then z is a split-complex number and conventionally j replaces epsilon. Then

${\displaystyle zz^{\ast }=(x+y\mathbf {j} )(x-y\mathbf {j} )=x^{2}-y^{2}\!}$

and {z | z z* = 1} is the unit hyperbola.

When ε² = 0, then z is a dual number.^[26]

This approach to non-Euclidean geometry explains the non-Euclidean angles: the parameters of slope in the dual number plane and hyperbolic angle in the split-complex plane correspond to angle in Euclidean geometry. Indeed, they each arise in polar decomposition of a complex number z.^[27]

Kinematic geometries

Hyperbolic geometry found an application in kinematics with the physical cosmology introduced by Hermann Minkowski in 1908. Minkowski introduced terms like worldline and proper time into mathematical physics. He realized that the submanifold, of events one moment of proper time into the future, could be considered a hyperbolic space of three dimensions.^[28][29] Already in the 1890s Alexander Macfarlane was charting this submanifold through his Algebra of Physics and hyperbolic quaternions, though Macfarlane did not use cosmological language as Minkowski did in 1908. The relevant structure is now called the hyperboloid model of hyperbolic geometry.

The non-Euclidean planar algebras support kinematic geometries in the plane. For instance, the split-complex number z = e^aj can represent a spacetime event one moment into the future of a frame of reference of rapidity a. Furthermore, multiplication by z amounts to a Lorentz boost mapping the frame with rapidity zero to that with rapidity a.

Kinematic study makes use of the dual numbers ${\displaystyle z=x+y\epsilon ,\quad \epsilon ^{2}=0,}$ to represent the classical description of motion in absolute time and space: The equations ${\displaystyle x^{\prime }=x+vt,\quad t^{\prime }=t}$ are equivalent to a shear mapping in linear algebra:

${\displaystyle {\begin{pmatrix}x'\\t'\end{pmatrix}}={\begin{pmatrix}1&v\\0&1\end{pmatrix}}{\begin{pmatrix}x\\t\end{pmatrix}}.}$

With dual numbers the mapping is ${\displaystyle t^{\prime }+x^{\prime }\epsilon =(1+v\epsilon )(t+x\epsilon )=t+(x+vt)\epsilon .}$^[30]

Another view of special relativity as a non-Euclidean geometry was advanced by E. B. Wilson and Gilbert Lewis in Proceedings of the American Academy of Arts and Sciences in 1912. They revamped the analytic geometry implicit in the split-complex number algebra into synthetic geometry of premises and deductions.^[31][32]

Fiction

Non-Euclidean geometry often makes appearances in works of science fiction and fantasy.

• In 1895 H. G. Wells published the short story "The Remarkable Case of Davidson’s Eyes". To appreciate this story one should know how antipodal points on a sphere are identified in a model of the elliptic plane. In the story, in the midst of a thunderstorm, Sidney Davidson sees "Waves and a remarkably neat schooner" while working in an electrical laboratory at Harlow Technical College. At the story’s close Davidson proves to have witnessed H.M.S. Fulmar off Antipodes Island.
• Non-Euclidean geometry is sometimes connected with the influence of the 20th century horror fiction writer H. P. Lovecraft. In his works, many unnatural things follow their own unique laws of geometry: In Lovecraft's Cthulhu Mythos, the sunken city of R'lyeh is characterized by its non-Euclidean geometry. It is heavily implied this is achieved as a side effect of not following the natural laws of this universe rather than simply using an alternate geometric model, as the sheer innate wrongness of it is said to be capable of driving those who look upon it insane.^[33]
• The main character in Robert Pirsig's Zen and the Art of Motorcycle Maintenance mentioned Riemannian Geometry on multiple occasions.
• In The Brothers Karamazov, Dostoevsky discusses non-Euclidean geometry through his main character Ivan.
• Christopher Priest's novel Inverted World describes the struggle of living on a planet with the form of a rotating pseudosphere.
• Robert Heinlein's The Number of the Beast utilizes non-Euclidean geometry to explain instantaneous transport through space and time and between parallel and fictional universes.
• Alexander Bruce's Antichamber uses non-Euclidean geometry to create a minimal, Escher-like world, where geometry and space follow unfamiliar rules.
• Zeno Rogue's HyperRogue is a roguelike game set on the hyperbolic plane, allowing the player to experience many properties of this geometry. Many mechanics, quests, and locations are strongly dependent on the features of hyperbolic geometry.^[34]
• In the Renegade Legion science fiction setting for FASA's wargame, role-playing-game and fiction, faster-than-light travel and communications is possible through the use of Hsieh Ho's Polydimensional Non-Euclidean Geometry, published sometime in the middle of the 22nd century.
• In Ian Stewart's Flatterland the protagonist Victoria Line visit all kinds of non-Euclidean worlds.
• In Jean-Pierre Petit's Here's looking at Euclid (and not looking at Euclid) Archibald Higgins stumbles upon spherical geometry^[35]

Bernhard Riemann

From Wikipedia, the free encyclopedia

Bernhard Riemann
Bernhard Riemann in 1863.
Born	Georg Friedrich Bernhard Riemann 17 September 1826 Breselenz, Kingdom of Hanover (modern-day Germany)
Died	20 July 1866 (aged 39) Selasca, Kingdom of Italy
Residence	Kingdom of Hanover
Nationality	German
Alma mater	University of Göttingen University of Berlin
Known for	See list
Scientific career
Fields	Mathematics Physics
Institutions	University of Göttingen
Thesis	Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen complexen Größe (1851)
Doctoral advisor	Carl Friedrich Gauss
Other academic advisors	Gotthold Eisenstein Moritz A. Stern Carl W. B. Goldschmidt
Notable students	Gustav Roch
Influences	J. P. G. L. Dirichlet
Signature

Georg Friedrich Bernhard Riemann (German: [ˈʀiːman] ( listen); 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His famous 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as one of the most influential papers in analytic number theory. Through his pioneering contributions to differential geometry, Bernhard Riemann laid the foundations of the mathematics of general relativity.

Biography

Early years

Riemann was born on September 17, 1826 in Breselenz, a village near Dannenberg in the Kingdom of Hanover. His father, Friedrich Bernhard Riemann, was a poor Lutheran pastor in Breselenz who fought in the Napoleonic Wars. His mother, Charlotte Ebell, died before her children had reached adulthood. Riemann was the second of six children, shy and suffering from numerous nervous breakdowns. Riemann exhibited exceptional mathematical skills, such as calculation abilities, from an early age but suffered from timidity and a fear of speaking in public.

Education

During 1840, Riemann went to Hanover to live with his grandmother and attend lyceum (middle school). After the death of his grandmother in 1842, he attended high school at the Johanneum Lüneburg. In high school, Riemann studied the Bible intensively, but he was often distracted by mathematics. His teachers were amazed by his adept ability to perform complicated mathematical operations, in which he often outstripped his instructor's knowledge. In 1846, at the age of 19, he started studying philology and Christian theology in order to become a pastor and help with his family's finances.

During the spring of 1846, his father, after gathering enough money, sent Riemann to the University of Göttingen, where he planned to study towards a degree in Theology. However, once there, he began studying mathematics under Carl Friedrich Gauss (specifically his lectures on the method of least squares). Gauss recommended that Riemann give up his theological work and enter the mathematical field; after getting his father's approval, Riemann transferred to the University of Berlin in 1847.^[1] During his time of study, Jacobi, Lejeune Dirichlet, Steiner, and Eisenstein were teaching. He stayed in Berlin for two years and returned to Göttingen in 1849.

Academia

Riemann held his first lectures in 1854, which founded the field of Riemannian geometry and thereby set the stage for Einstein's general theory of relativity. In 1857, there was an attempt to promote Riemann to extraordinary professor status at the University of Göttingen. Although this attempt failed, it did result in Riemann finally being granted a regular salary. In 1859, following Lejeune Dirichlet's death, he was promoted to head the mathematics department at Göttingen. He was also the first to suggest using dimensions higher than merely three or four in order to describe physical reality.^[2] In 1862 he married Elise Koch and had a daughter.

Austro-Prussian War and death in Italy

Riemann's tombstone in Biganzolo

Riemann fled Göttingen when the armies of Hanover and Prussia clashed there in 1866.^[3] He died of tuberculosis during his third journey to Italy in Selasca (now a hamlet of Verbania on Lake Maggiore) where he was buried in the cemetery in Biganzolo (Verbania). Riemann was a dedicated Christian, the son of a Protestant minister, and saw his life as a mathematician as another way to serve God. During his life, he held closely to his Christian faith and considered it to be the most important aspect of his life. At the time of his death, he was reciting the Lord’s Prayer with his wife and died before they finished saying the prayer.^[4] Meanwhile, in Göttingen his housekeeper discarded some of the papers in his office, including much unpublished work. Riemann refused to publish incomplete work, and some deep insights may have been lost forever.^[3]

Riemann's tombstone in Biganzolo (Italy) refers to Romans 8:28 ("And we know that all things work together for good to them that love God, to them who are called according to his purpose"):

Here rests in God Georg Friedrich Bernhard Riemann
Professor in Göttingen
born in Breselenz, Germany 17 September 1826
died in Selasca, Italy 20 July 1866
For those who love God, all things must work together for the best.^[5]

Riemannian geometry

Riemann's published works opened up research areas combining analysis with geometry. These would subsequently become major parts of the theories of Riemannian geometry, algebraic geometry, and complex manifold theory. The theory of Riemann surfaces was elaborated by Felix Klein and particularly Adolf Hurwitz. This area of mathematics is part of the foundation of topology and is still being applied in novel ways to mathematical physics.

In 1853, Gauss asked his student Riemann to prepare a Habilitationsschrift on the foundations of geometry. Over many months, Riemann developed his theory of higher dimensions and delivered his lecture at Göttingen in 1854 entitled "Ueber die Hypothesen welche der Geometrie zu Grunde liegen" ("On the hypotheses which underlie geometry"). It was only published twelve years later in 1868 by Dedekind, two years after his death. Its early reception appears to have been slow but it is now recognized as one of the most important works in geometry.

The subject founded by this work is Riemannian geometry. Riemann found the correct way to extend into n dimensions the differential geometry of surfaces, which Gauss himself proved in his theorema egregium. The fundamental object is called the Riemann curvature tensor. For the surface case, this can be reduced to a number (scalar), positive, negative, or zero; the non-zero and constant cases being models of the known non-Euclidean geometries.

Riemann's idea was to introduce a collection of numbers at every point in space (i.e., a tensor) which would describe how much it was bent or curved. Riemann found that in four spatial dimensions, one needs a collection of ten numbers at each point to describe the properties of a manifold, no matter how distorted it is. This is the famous construction central to his geometry, known now as a Riemannian metric.

Complex analysis

In his dissertation, he established a geometric foundation for complex analysis through Riemann surfaces, through which multi-valued functions like the logarithm (with infinitely many sheets) or the square root (with two sheets) could become one-to-one functions. Complex functions are harmonic functions (that is, they satisfy Laplace's equation and thus the Cauchy–Riemann equations) on these surfaces and are described by the location of their singularities and the topology of the surfaces. The topological "genus" of the Riemann surfaces is given by ${\displaystyle g=w/2-n+1}$, where the surface has ${\displaystyle n}$ leaves coming together at ${\displaystyle w}$ branch points. For ${\displaystyle g>1}$ the Riemann surface has ${\displaystyle (3g-3)}$ parameters (the "moduli").

His contributions to this area are numerous. The famous Riemann mapping theorem says that a simply connected domain in the complex plane is "biholomorphically equivalent" (i.e. there is a bijection between them that is holomorphic with a holomorphic inverse) to either ${\displaystyle \mathbb {C} }$ or to the interior of the unit circle. The generalization of the theorem to Riemann surfaces is the famous uniformization theorem, which was proved in the 19th century by Henri Poincaré and Felix Klein. Here, too, rigorous proofs were first given after the development of richer mathematical tools (in this case, topology). For the proof of the existence of functions on Riemann surfaces he used a minimality condition, which he called the Dirichlet principle. Weierstrass found a gap in the proof: Riemann had not noticed that his working assumption (that the minimum existed) might not work; the function space might not be complete, and therefore the existence of a minimum was not guaranteed. Through the work of David Hilbert in the Calculus of Variations, the Dirichlet principle was finally established. Otherwise, Weierstrass was very impressed with Riemann, especially with his theory of abelian functions. When Riemann's work appeared, Weierstrass withdrew his paper from Crelle's Journal and did not publish it. They had a good understanding when Riemann visited him in Berlin in 1859. Weierstrass encouraged his student Hermann Amandus Schwarz to find alternatives to the Dirichlet principle in complex analysis, in which he was successful. An anecdote from Arnold Sommerfeld^[6] shows the difficulties which contemporary mathematicians had with Riemann's new ideas. In 1870, Weierstrass had taken Riemann's dissertation with him on a holiday to Rigi and complained that it was hard to understand. The physicist Hermann von Helmholtz assisted him in the work over night and returned with the comment that it was "natural" and "very understandable".

Other highlights include his work on abelian functions and theta functions on Riemann surfaces. Riemann had been in a competition with Weierstrass since 1857 to solve the Jacobian inverse problems for abelian integrals, a generalization of elliptic integrals. Riemann used theta functions in several variables and reduced the problem to the determination of the zeros of these theta functions. Riemann also investigated period matrices and characterized them through the "Riemannian period relations" (symmetric, real part negative). By Ferdinand Georg Frobenius and Solomon Lefschetz the validity of this relation is equivalent with the embedding of ${\displaystyle C^{n}/\Omega }$ (where ${\displaystyle \Omega }$ is the lattice of the period matrix) in a projective space by means of theta functions. For certain values of ${\displaystyle n}$, this is the Jacobian variety of the Riemann surface, an example of an abelian manifold.

Many mathematicians such as Alfred Clebsch furthered Riemann's work on algebraic curves. These theories depended on the properties of a function defined on Riemann surfaces. For example, the Riemann–Roch theorem (Roch was a student of Riemann) says something about the number of linearly independent differentials (with known conditions on the zeros and poles) of a Riemann surface.

According to Laugwitz,^[7] automorphic functions appeared for the first time in an essay about the Laplace equation on electrically charged cylinders. Riemann however used such functions for conformal maps (such as mapping topological triangles to the circle) in his 1859 lecture on hypergeometric functions or in his treatise on minimal surfaces.

Real analysis

In the field of real analysis, he discovered the Riemann integral in his habilitation. Among other things, he showed that every piecewise continuous function is integrable. Similarly, the Stieltjes integral goes back to the Göttinger mathematician, and so they are named together the Riemann–Stieltjes integral.

In his habilitation work on Fourier series, where he followed the work of his teacher Dirichlet, he showed that Riemann-integrable functions are "representable" by Fourier series. Dirichlet has shown this for continuous, piecewise-differentiable functions (thus with countably many non-differentiable points). Riemann gave an example of a Fourier series representing a continuous, almost nowhere-differentiable function, a case not covered by Dirichlet. He also proved the Riemann–Lebesgue lemma: if a function is representable by a Fourier series, then the Fourier coefficients go to zero for large n.

Riemann's essay was also the starting point for Georg Cantor's work with Fourier series, which was the impetus for set theory.

He also worked with hypergeometric differential equations in 1857 using complex analytical methods and presented the solutions through the behavior of closed paths about singularities (described by the monodromy matrix). The proof of the existence of such differential equations by previously known monodromy matrices is one of the Hilbert problems.

Number theory

He made some famous contributions to modern analytic number theory. In a single short paper, the only one he published on the subject of number theory, he investigated the zeta function that now bears his name, establishing its importance for understanding the distribution of prime numbers. The Riemann hypothesis was one of a series of conjectures he made about the function's properties.

In Riemann's work, there are many more interesting developments. He proved the functional equation for the zeta function (already known to Euler), behind which a theta function lies. Also, it gives a better approximation for the prime-counting function ${\displaystyle \pi (x)}$ than Gauss's function ${\displaystyle Li(x)}$^{[citation needed]}. Through the summation of this approximation function over the non-trivial zeros on the line with real portion 1/2, he gave an exact, "explicit formula" for ${\displaystyle \pi (x)}$.

Riemann knew Chebyshev's work on the Prime Number Theorem. He had visited Dirichlet in 1852. But Riemann's methods were very different.

Writings

1868 On the hypotheses which lie at the foundation of geometry, translated by W.K.Clifford, Nature 8 1873 183 – reprinted in Clifford's Collected Mathematical Papers, London 1882 (MacMillan); New York 1968 (Chelsea) http://www.emis.de/classics/Riemann/. Also in Ewald, William B., ed., 1996 “From Kant to Hilbert: A Source Book in the Foundations of Mathematics”, 2 vols. Oxford Uni. Press: 652–61.

1892 Collected Works of Bernhardt Riemann (H. Weber ed). In German. Reprinted New York 1953 (Dover)

Riemann, Bernhard (2004), Collected papers, Kendrick Press, Heber City, UT, ISBN 978-0-9740427-2-5, MR 2121437