Language processing in the brain

From Wikipedia, the free encyclopedia

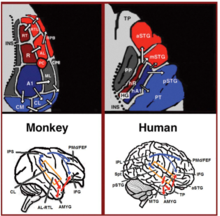
Dual stream connectivity between the auditory cortex and frontal lobe of monkeys and humans. Top: The auditory cortex of the monkey (left) and human (right) is schematically depicted on the supratemporal plane and observed from above (with the parieto- frontal operculi removed). Bottom: The brain of the monkey (left) and human (right) is schematically depicted and displayed from the side. Orange frames mark the region of the auditory cortex, which is displayed in the top sub-figures. Top and Bottom: Blue colors mark regions affiliated with the ADS, and red colors mark regions affiliated with the AVS (dark red and blue regions mark the primary auditory fields). Abbreviations: AMYG-amygdala, HG-Heschl’s gyrus, FEF-frontal eye field, IFG-inferior frontal gyrus, INS-insula, IPS-intra parietal sulcus, MTG-middle temporal gyrus, PC-pitch center, PMd-dorsal premotor cortex, PP-planum polare, PT-planum temporale, TP-temporal pole, Spt-sylvian parietal-temporal, pSTG/mSTG/aSTG-posterior/middle/anterior superior temporal gyrus, CL/ ML/AL/RTL-caudo-/middle-/antero-/rostrotemporal-lateral belt area, CPB/RPB-caudal/rostral parabelt fields.

Language processing refers to the way humans use words to communicate ideas and feelings, and how such communications are processed and understood. Language processing is considered to be an uniquely human ability that is not produced with the same grammatical understanding or systematicity in even human's closest primate relatives.

Throughout the 20th century the dominant model for language processing in the brain was the Geschwind-Lichteim-Wernicke model, which is based primarily on the analysis of brain damaged patients. However, due to improvements in intra-cortical electrophysiological recordings of monkey and human brains, as well non-invasive techniques such as fMRI, PET, MEG and EEG, a dual auditory pathway has been revealed. In accordance with this model, there are two pathways that connect the auditory cortex to the frontal lobe, each pathway accounting for different linguistic roles. The auditory ventral stream connects the auditory cortex with the middle temporal gyrus and temporal pole, which in turn connects with the inferior frontal gyrus. This pathway is responsible for sound recognition, and is accordingly known as the auditory 'what' pathway. The auditory dorsal stream connects the auditory cortex with the parietal lobe, which in turn connects with inferior frontal gyrus. In both humans and non-human primates, the auditory dorsal stream is responsible for sound localization, and is accordingly known as the auditory 'where' pathway. In humans, this pathway (especially in the left hemisphere) is also responsible for speech production, speech repetition, lip-reading, and phonological working memory and long-term memory. In accordance with the 'from where to what' model of language evolution. the reason the ADS is characterized with such a broad range of functions is that each indicates a different stage in language evolution.

History of neurolinguistics

Throughout the 20th century, our knowledge of language processing in the brain was dominated by the Wernicke-Lichtheim-Geschwind model. This model is primarily based on research conducted on brain-damaged individuals who were reported to possess a variety of language related disorders. In accordance with this model, words are perceived via a specialized word reception center (Wernicke’s area) that is located in the left temporoparietal junction. This region then projects to a word production center (Broca’s area) that is located in the left inferior frontal gyrus. Because almost all language input was thought to funnel via Wernicke’s area and all language output to funnel via Broca’s area, it became extremely difficult to identify the basic properties of each region. This lack of clear definition for the contribution of Wernicke’s and Broca’s regions to human language rendered it extremely difficult to identify their homologues in other primates. With the advent of the MRI and its application for lesion mappings, however, it was shown that this model is based on incorrect correlations between symptoms and lesions. The refutation of such an influential and dominant model opened the door to new models of language processing in the brain.

Anatomy of the auditory ventral and dorsal streams

In the last two decades, significant advances occurred in our understanding of the neural processing of sounds in primates. Initially by recording of neural activity in the auditory cortices of monkeys and later elaborated via histological staining and fMRI scanning studies, 3 auditory fields were identified in the primary auditory cortex, and 9 associative auditory fields were shown to surround them (Figure 1 top left). Anatomical tracing and lesion studies further indicated of a separation between the anterior and posterior auditory fields, with the anterior primary auditory fields (areas R-RT) projecting to the anterior associative auditory fields (areas AL-RTL), and the posterior primary auditory field (area A1) projecting to the posterior associative auditory fields (areas CL-CM). Recently, evidence accumulated that indicates homology between the human and monkey auditory fields. In humans, histological staining studies revealed two separate auditory fields in the primary auditory region of Heschl’s gyrus, and by mapping the tonotopic organization of the human primary auditory fields with high resolution fMRI and comparing it to the tonotopic organization of the monkey primary auditory fields, homology was established between the human anterior primary auditory field and monkey area R (denoted in humans as area hR) and the human posterior primary auditory field and the monkey area A1 (denoted in humans as area hA1). Intra-cortical recordings from the human auditory cortex further demonstrated similar patterns of connectivity to the auditory cortex of the monkey. Recording from the surface of the auditory cortex (supra-temporal plane) reported that the anterior Heschl’s gyrus (area hR) projects primarily to the middle-anterior superior temporal gyrus (mSTG-aSTG) and the posterior Heschl’s gyrus (area hA1) projects primarily to the posterior superior temporal gyrus (pSTG) and the planum temporale (area PT; Figure 1 top right). Consistent with connections from area hR to the aSTG and hA1 to the pSTG is an fMRI study of a patient with impaired sound recognition (auditory agnosia), who was shown with reduced bilateral activation in areas hR and aSTG but with spared activation in the mSTG-pSTG. This connectivity pattern is also corroborated by a study that recorded activation from the lateral surface of the auditory cortex and reported of simultaneous non-overlapping activation clusters in the pSTG and mSTG-aSTG while listening to sounds.

Downstream to the auditory cortex, anatomical tracing studies in monkeys delineated projections from the anterior associative auditory fields (areas AL-RTL) to ventral prefrontal and premotor cortices in the inferior frontal gyrus (IFG) and amygdala. Cortical recording and functional imaging studies in macaque monkeys further elaborated on this processing stream by showing that acoustic information flows from the anterior auditory cortex to the temporal pole (TP) and then to the IFG. This pathway is commonly referred to as the auditory ventral stream (AVS; Figure 1, bottom left-red arrows). In contrast to the anterior auditory fields, tracing studies reported that the posterior auditory fields (areas CL-CM) project primarily to dorsolateral prefrontal and premotor cortices (although some projections do terminate in the IFG. Cortical recordings and anatomical tracing studies in monkeys further provided evidence that this processing stream flows from the posterior auditory fields to the frontal lobe via a relay station in the intra-parietal sulcus (IPS). This pathway is commonly referred to as the auditory dorsal stream (ADS; Figure 1, bottom left-blue arrows). Comparing the white matter pathways involved in communication in humans and monkeys with diffusion tensor imaging techniques indicates of similar connections of the AVS and ADS in the two species (Monkey, Human). In humans, the pSTG was shown to project to the parietal lobe (sylvian parietal-temporal junction- inferior parietal lobule; Spt-IPL), and from there to dorsolateral prefrontal and premotor cortices (Figure 1, bottom right-blue arrows), and the aSTG was shown to project to the anterior temporal lobe (middle temporal gyrus-temporal pole; MTG-TP) and from there to the IFG (Figure 1 bottom right-red arrows).

Auditory ventral stream

Sound Recognition

Accumulative converging evidence indicates that the AVS is involved in recognizing auditory objects. At the level of the primary auditory cortex, recordings from monkeys showed higher percentage of neurons selective for learned melodic sequences in area R than area A1, and a study in humans demonstrated more selectivity for heard syllables in the anterior Heschl’s gyrus (area hR) than posterior Heshcl’s gyrus (area hA1). In downstream associative auditory fields, studies from both monkeys and humans reported that the border between the anterior and posterior auditory fields (Figure 1-area PC in the monkey and mSTG in the human) processes pitch attributes that are necessary for the recognition of auditory objects. The anterior auditory fields of monkeys were also demonstrated with selectivity for con-specific vocalizations with intra-cortical recordings and functional imaging One fMRI monkey study further demonstrated a role of the aSTG in the recognition of individual voices. The role of the human mSTG-aSTG in sound recognition was demonstrated via functional imaging studies that correlated activity in this region with isolation of auditory objects from background noise, and with the recognition of spoken words, voices, melodies, environmental sounds, and non-speech communicative sounds. A Meta-analysis of fMRI studies further demonstrated functional dissociation between the left mSTG and aSTG, with the former processing short speech units (phonemes) and the latter processing longer units (e.g., words, environmental sounds). A study that recorded neural activity directly from the left pSTG and aSTG reported that the aSTG, but not pSTG, was more active when the patient listened to speech in her native language than unfamiliar foreign language. Consistently, electro stimulation to the aSTG of this patient resulted in impaired speech perception. Intra-cortical recordings from the right and left aSTG further demonstrated that speech is processed laterally to music. An fMRI study of a patient with impaired sound recognition (auditory agnosia) due to brainstem damage was also shown with reduced activation in areas hR and aSTG of both hemispheres when hearing spoken words and environmental sounds. Recordings from the anterior auditory cortex of monkeys while maintaining learned sounds in working memory, and the debilitating effect of induced lesions to this region on working memory recall, further implicate the AVS in maintaining the perceived auditory objects in working memory. In humans, area mSTG-aSTG was also reported active during rehearsal of heard syllables with MEG and fMRI. The latter study further demonstrated that working memory in the AVS is for the acoustic properties of spoken words and that it is independent to working memory in the ADS, which mediates inner speech. Working memory studies in monkeys also suggest that in monkeys, in contrast to humans, the AVS is the dominant working memory store.

In humans, downstream to the aSTG, the MTG and TP are thought to constitute the semantic lexicon, which is a long-term memory repository of audio-visual representations that are interconnected on the basis of semantic relationships. The primary evidence for this role of the MTG-TP is that patients with damage to this region (e.g., patients with semantic dementia or herpes simplex virus encephalitis) are reported with an impaired ability to describe visual and auditory objects and a tendency to commit semantic errors when naming objects (i.e., semantic paraphasia). Semantic paraphasias were also expressed by aphasic patients with left MTG-TP damage and were shown to occur in non-aphasic patients after electro-stimulation to this region or the underlying white matter pathway. Two meta-analyses of the fMRI literature also reported that the anterior MTG and TP were consistently active during semantic analysis of speech and text; and an intra-cortical recording study correlated neural discharge in the MTG with the comprehension of intelligible sentences.

Sentence comprehension

In addition to extracting meaning from sounds, the MTG-TP region of the AVS appears to have a role in sentence comprehension, possibly by merging concepts together (e.g., merging the concept 'blue' and 'shirt to create the concept of a 'blue shirt'). The role of the MTG in extracting meaning from sentences has been demonstrated in functional imaging studies reporting stronger activation in the anterior MTG when proper sentences are contrasted with lists of words, sentences in a foreign or nonsense language, scrambled sentences, sentences with semantic or syntactic violations and sentence-like sequences of environmental sounds. One fMRI study in which participants were instructed to read a story further correlated activity in the anterior MTG with the amount of semantic and syntactic content each sentence contained. An EEG study that contrasted cortical activity while reading sentences with and without syntactic violations in healthy participants and patients with MTG-TP damage, concluded that the MTG-TP in both hemispheres participate in the automatic (rule based) stage of syntactic analysis (ELAN component), and that the left MTG-TP is also involved in a later controlled stage of syntax analysis (P600 component). Patients with damage to the MTG-TP region have also been reported with impaired sentence comprehension.

Bilaterality

In contradiction to the Wernicke-Lichtheim-Geschwind model that implicates sound recognition to occur solely in the left hemisphere, studies that examined the properties of the right or left hemisphere in isolation via unilateral hemispheric anesthesia (i.e., the WADA procedure) or intra-cortical recordings from each hemisphere provided evidence that sound recognition is processed bilaterally. Moreover, a study that instructed patients with disconnected hemispheres (i.e., split-brain patients) to match spoken words to written words presented to the right or left hemifields, reported vocabulary in the right hemisphere that almost matches in size with the left hemisphere (the right hemisphere vocabulary was equivalent to the vocabulary of a healthy 11-years old child). This bilateral recognition of sounds is also consistent with the finding that unilateral lesion to the auditory cortex rarely results in deficit to auditory comprehension (i.e., auditory agnosia), whereas a second lesion to the remaining hemisphere (which could occur years later) does. Finally, as mentioned earlier, an fMRI scan of an auditory agnosia patient demonstrated bilateral reduced activation in the anterior auditory cortices, and bilateral electro-stimulation to these regions in both hemispheres resulted with impaired speech recognition.

Auditory dorsal stream

Sound localization

The most established role of the ADS is with audiospatial processing. This is evidenced via studies that recorded neural activity from the auditory cortex of monkeys, and correlated the strongest selectivity to changes in sound location with the posterior auditory fields (areas CM-CL), intermediate selectivity with primary area A1, and very weak selectivity with the anterior auditory fields. In humans, behavioral studies of brain damaged patients and EEG recordings from healthy participants demonstrated that sound localization is processed independently of sound recognition, and thus is likely independent of processing in the AVS. Consistently, a working memory study reported two independent working memory storage spaces, one for acoustic properties and one for locations. Functional imaging studies that contrasted sound discrimination and sound localization reported a correlation between sound discrimination and activation in the mSTG-aSTG, and correlation between sound localization and activation in the pSTG and PT, with some studies further reporting of activation in the Spt-IPL region and frontal lobe. Some fMRI studies also reported that the activation in the pSTG and Spt-IPL regions increased when individuals perceived sounds in motion. EEG studies using source-localization also identified the pSTG-Spt region of the ADS as the sound localization processing center. A combined fMRI and MEG study corroborated the role of the ADS with audiospatial processing by demonstrating that changes in sound location resulted in activation spreading from Heschl’s gyrus posteriorly along the pSTG and terminating in the IPL. In another MEG study, the IPL and frontal lobe were shown active during maintenance of sound locations in working memory.

Guidance of eye movements

In addition to localizing sounds, the ADS appears also to encode the sound location in memory, and to use this information for guiding eye movements. Evidence for the role of the ADS in encoding sounds into working memory is provided via studies that trained monkeys in a delayed matching to sample task, and reported of activation in areas CM-CL and IPS during the delay phase. Influence of this spatial information on eye movements occurs via projections of the ADS into the frontal eye field (FEF; a premotor area that is responsible for guiding eye movements) located in the frontal lobe. This is demonstrated with anatomical tracing studies that reported of connections between areas CM-CL-IPS and the FEF, and electro-physiological recordings that reported neural activity in both the IPS and the FEF prior to conducting saccadic eye-movements toward auditory targets.

Integration of locations with auditory objects

A surprising function of the ADS is with the discrimination and possible identification of sounds, which is commonly ascribed with the anterior STG and STS of the AVS. However, electrophysiological recordings from the posterior auditory cortex (areas CM-CL), and IPS of monkeys, as well a PET monkey study reported of neurons that are selective to monkey vocalizations. One of these studies also reported of neurons in areas CM-CL that are characterized with dual selectivity for both a vocalization and a sound location. A monkey study that recorded electrophysiological activity from neurons in the posterior insula also reported of neurons that discriminate monkey calls based on the identity of the speaker. Similarly, human fMRI studies that instructed participants to discriminate voices reported an activation cluster in the pSTG. A study that recorded activity from the auditory cortex of an epileptic patient further reported that the pSTG, but not aSTG, was selective for the presence of a new speaker. A study that scanned fetuses in their third trimester of pregnancy with fMRI further reported of activation in area Spt when the hearing of voices was contrasted to pure tones. The researchers also reported that a sub-region of area Spt was more selective to their mother’s voice than unfamiliar female voices. This study thus suggests that the ADS is capable of identifying voices in addition to discriminating them.

The manner in which sound recognition in the pSTG-PT-Spt regions of the ADS differs from sound recognition in the anterior STG and STS of the AVS was shown via electro-stimulation of an epileptic patient. This study reported that electro-stimulation of the aSTG resulted in changes in the perceived pitch of voices (including the patient’s own voice), whereas electro-stimulation of the pSTG resulted in reports that her voice was “drifting away.” This report indicates a role for the pSTG in the integration of sound location with an individual voice. Consistent with this role of the ADS is a study that reported patients, with AVS damage but spared ADS (surgical removal of the anterior STG/MTG), were no longer capable of isolating environmental sounds in the contralesional space, whereas their ability of isolating and discriminating human voices remained intact. Supporting a role for the pSTG-PT-Spt of the ADS with integrating auditory objects with sound locations are also studies that demonstrate a role for this region in the isolation of specific sounds. For example, two functional imaging studies correlated circumscribed pSTG-PT activation with the spreading of sounds into an increasing number of locations. Accordingly, an fMRI study correlated the perception of acoustic cues that are necessary for separating musical sounds (pitch chroma) with pSTG-PT activation.

Integration of phonemes with lip-movements

Although sound perception is primarily ascribed with the AVS, the ADS appears associated with several aspects of speech perception. For instance, in a meta-analysis of fMRI studies in which the auditory perception of phonemes was contrasted with closely matching sounds, and the studies were rated for the required level of attention, the authors concluded that attention to phonemes correlates with strong activation in the pSTG-pSTS region. An intra-cortical recording study in which participants were instructed to identify syllables also correlated the hearing of each syllable with its own activation pattern in the pSTG. Consistent with the role of the ADS in discriminating phonemes, studies have ascribed the integration of phonemes and their corresponding lip movements (i.e., visemes) to the pSTS of the ADS. For example, an fMRI study has correlated activation in the pSTS with the McGurk illusion (in which hearing the syllable “ba” while seeing the viseme “ga” results in the perception of the syllable “da”). Another study has found that using magnetic stimulation to interfere with processing in this area further disrupts the McGurk illusion. The association of the pSTS with the audio-visual integration of speech has also been demonstrated in a study that presented participants with pictures of faces and spoken words of varying quality. The study reported that the pSTS selects for the combined increase of the clarity of faces and spoken words. Corroborating evidence has been provided by an fMRI study that contrasted the perception of audio-visual speech with audio-visual non-speech (pictures and sounds of tools). This study reported the detection of speech-selective compartments in the pSTS. In addition, an fMRI study that contrasted congruent audio-visual speech with incongruent speech (pictures of still faces) reported pSTS activation.

Phonological long-term memory

A growing body of evidence indicates that humans, in addition to having a long-term store for word meanings located in the MTG-TP of the AVS (i.e., the semantic lexicon), also have a long-term store for the names of objects located in the Spt-IPL region of the ADS (i.e., the phonological lexicon). For example, a study examining patients with damage to the AVS (MTG damage) or damage to the ADS (IPL damage) reported that MTG damage results in individuals incorrectly identifying objects (e.g., calling a “goat” a “sheep,” an example of semantic paraphasia). Conversely, IPL damage results in individuals correctly identifying the object but incorrectly pronouncing its name (e.g., saying “gof” instead of “goat,” an example of phonemic paraphasia). Semantic paraphasia errors have also been reported in patients receiving intra-cortical electrical stimulation of the AVS (MTG), and phonemic paraphasia errors have been reported in patients whose ADS (pSTG, Spt, and IPL) received intra-cortical electrical stimulation. Further supporting the role of the ADS in object naming is an MEG study that localized activity in the IPL during the learning and during the recall of object names. A study that induced magnetic interference in participants’ IPL while they answered questions about an object reported that the participants were capable of answering questions regarding the object’s characteristics or perceptual attributes but were impaired when asked whether the word contained two or three syllables. An MEG study has also correlated recovery from anomia (a disorder characterized by an impaired ability to name objects) with changes in IPL activation. Further supporting the role of the IPL in encoding the sounds of words are studies reporting that, compared to monolinguals, bilinguals have greater cortical density in the IPL but not the MTG. Because evidence shows that, in bilinguals, different phonological representations of the same word share the same semantic representation, this increase in density in the IPL verifies the existence of the phonological lexicon: the semantic lexicon of bilinguals is expected to be similar in size to the semantic lexicon of monolinguals, whereas their phonological lexicon should be twice the size. Consistent with this finding, cortical density in the IPL of monolinguals also correlates with vocabulary size. Notably, the functional dissociation of the AVS and ADS in object-naming tasks is supported by cumulative evidence from reading research showing that semantic errors are correlated with MTG impairment and phonemic errors with IPL impairment. Based on these associations, the semantic analysis of text has been linked to the inferior-temporal gyrus and MTG, and the phonological analysis of text has been linked to the pSTG-Spt- IPL.

Phonological working memory

Working memory is often treated as the temporary activation of the representations stored in long-term memory that are used for speech (phonological representations). This sharing of resources between working memory and speech is evident by the finding that speaking during rehearsal results in a significant reduction in the number of items that can be recalled from working memory (articulatory suppression). The involvement of the phonological lexicon in working memory is also evidenced by the tendency of individuals to make more errors when recalling words from a recently learned list of phonologically similar words than from a list of phonologically dissimilar words (the phonological similarity effect). Studies have also found that speech errors committed during reading are remarkably similar to speech errors made during the recall of recently learned, phonologically similar words from working memory. Patients with IPL damage have also been observed to exhibit both speech production errors and impaired working memory. Finally, the view that verbal working memory is the result of temporarily activating phonological representations in the ADS is compatible with recent models describing working memory as the combination of maintaining representations in the mechanism of attention in parallel to temporarily activating representations in long-term memory. It has been argued that the role of the ADS in the rehearsal of lists of words is the reason this pathway is active during sentence comprehension For a review of the role of the ADS in working memory, see.

The 'from where to what' model of language evolution hypotheses 7 stages of language evolution: 1. The origin of speech is the exchange of contact calls between mothers and offspring used to relocate each other in cases of separation. 2. Offspring of early Homo modified the contact calls with intonations in order to emit two types of contact calls: contact calls that signal low level of distress and contact calls that signal high-level of distress. 3. The use of two types of contact calls enabled the first question-answer conversation. In this scenario, the offspring emits a low-level distress call to express a desire to interact with an object, and the mother responds with a low-level distress call to enable the interaction or high-level distress call to prohibit it. 4. The use of intonations improved over time, and eventually, individuals acquired sufficient vocal control to invent new words to objects. 5. At first, offspring learned the calls from their parents by imitating their lip-movements. 6. As the learning of calls improved, babies learned new calls (i.e., phonemes) through lip imitation only during infancy. After that period, the memory of phonemes lasted for a lifetime, and older children became capable of learning new calls (through mimicry) without observing their parents' lip-movements. 7. Individuals became capable of rehearsing sequences of calls. This enabled the learning of words with several syllables, which increased vocabulary size. Further developments to the brain circuit responsible for rehearsing poly-syllabic words resulted with individuals capable of rehearsing lists of words (phonological working memory), which served as the platform for communication with sentences.

Evolution of language

It is presently unknown why so many functions are ascribed to the human ADS. An attempt to unify these functions under a single framework was conducted in the ‘From where to what’ model of language evolution. In accordance with this model, each function of the ADS indicates of a different intermediate phase in the evolution of language. The roles of sound localization and integration of sound location with voices and auditory objects is interpreted as evidence that the origin of speech is the exchange of contact calls (calls used to report location in cases of separation) between mothers and offspring. The role of the ADS in the perception and production of intonations is interpreted as evidence that speech began by modifying the contact calls with intonations, possibly for distinguishing alarm contact calls from safe contact calls. The role of the ADS in encoding the names of objects (phonological long-term memory) is interpreted as evidence of gradual transition from modifying calls with intonations to complete vocal control. The role of the ADS in the integration of lip movements with phonemes and in speech repetition is interpreted as evidence that spoken words were learned by infants mimicking their parents’ vocalizations, initially by imitating their lip movements. The role of the ADS in phonological working memory is interpreted as evidence that the words learned through mimicry remained active in the ADS even when not spoken. This resulted with individuals capable of rehearsing a list of vocalizations, which enabled the production of words with several syllables. Further developments in the ADS enabled the rehearsal of lists of words, which provided the infra-structure for communicating with sentences.

Automata-based programming

From Wikipedia, the free encyclopedia

Automata-based programming is a programming paradigm in which the program or part of it is thought of as a model of a finite state machine (FSM) or any other (often more complicated) formal automaton. Sometimes a potentially infinite set of possible states is introduced, and such a set can have a complicated structure, not just an enumeration.

FSM-based programming is generally the same, but, formally speaking, doesn't cover all possible variants, as FSM stands for finite state machine, and automata-based programming doesn't necessarily employ FSMs in the strict sense.

The following properties are key indicators for automata-based programming:

1. The time period of the program's execution is clearly separated down to the steps of the automaton. Each of the steps is effectively an execution of a code section (same for all the steps), which has a single entry point. Such a section can be a function or other routine, or just a cycle body. The step section might be divided down to subsections to be executed depending on different states, although this is not necessary.
2. Any communication between the steps is only possible via the explicitly noted set of variables named the state. Between any two steps, the program (or its part created using the automata-based technique) can not have implicit components of its state, such as local (stack) variables' values, return addresses, the current instruction pointer, etc. That is, the state of the whole program, taken at any two moments of entering the step of the automaton, can only differ in the values of the variables being considered as the state of the automaton.

The whole execution of the automata-based code is a (possibly explicit) cycle of the automaton's steps.

Another reason for using the notion of automata-based programming is that the programmer's style of thinking about the program in this technique is very similar to the style of thinking used to solve mathematical tasks using Turing machines, Markov algorithms, etc.

Example

Consider a program in C that reads a text from standard input stream, line by line, and prints the first word of each line. It is clear we need first to read and skip the leading spaces, if any, then read characters of the first word and print them until the word ends, and then read and skip all the remaining characters until the end-of-line character is encountered. Upon reaching the end of line character (regardless of the stage), we restart the algorithm from the beginning, and upon encountering the end of file condition (regardless of the stage), we terminate the program.  

Traditional (imperative) program in C

The program which solves the example task in traditional (imperative) style can look something like this:

#include 
#include 
int main(void)
{
    int c;
    do {
        do {
            c = getchar();
        } while(c == ' ');
        while(c != EOF && !isspace(c) && c != '\n') {
            putchar(c);
            c = getchar();
        }
        putchar('\n');
        while(c != EOF && c != '\n')
            c = getchar();
    } while(c != EOF);
    return 0;
}

Automata-based style program

The same task can be solved by thinking in terms of finite state machines. Note that line parsing has three stages: skipping the leading spaces, printing the word and skipping the trailing characters. Let's call them states before, inside and after. The program may now look like this:

#include 
#include 
int main(void)
{
    enum states {
        before, inside, after
    } state;
    int c;
    state = before;
    while((c = getchar()) != EOF) {
        switch(state) {
            case before:
                if(c != ' ') {
                    putchar(c);
                    if(c != '\n')
                        state = inside;
                }
                break; 
            case inside:
                if(!isspace(c))
                    putchar(c);
                else {
                    putchar('\n');
                    if(c == '\n')
                        state = before;
                    else
                        state = after;
                }
                break;
            case after:
                if(c == '\n')
                    state = before;
        }
    }
    return 0;
}

Although the code now looks longer, it has at least one significant advantage: there's only one reading (that is, call to the getchar() function) instruction in the program. Besides that, there's only one loop instead of the four the previous versions had.

In this program, the body of the while loop is the automaton step, and the loop itself is the cycle of the automaton's work. 

The program implements (models) the work of a finite state machine shown on the picture. The N denotes the end of line character, the S denotes spaces, and the A stands for all the other characters. The automaton follows exactly one arrow on each step depending on the current state and the encountered character. Some state switches are accompanied with printing the character; such arrows are marked with asterisks.

It is not absolutely necessary to divide the code down to separate handlers for each unique state. Furthermore, in some cases the very notion of the state can be composed of several variables' values, so that it could be impossible to handle each possible state explicitly. In the discussed program it is possible to reduce the code length by noticing that the actions taken in response to the end of line character are the same for all the possible states. The following program is equal to the previous one but is a bit shorter:

#include 
#include 
int main(void)
{
    enum states {
        before, inside, after
    } state;
    int c;
    state = before;
    while((c = getchar()) != EOF) {
        if(c == '\n') {
            putchar('\n');
            state = before;
        } else
        switch(state) {
            case before:
                if(c != ' ') {
                    putchar(c);
                    state = inside;
                }
                break;
            case inside:
                if(c == ' ') {
                    state = after;
                } else {
                    putchar(c);
                }
                break;
            case after:
                break;
        }
    }
    if(state != before)
        putchar('\n');
    return 0;
}

A separate function for the automation step

The most important property of the previous program is that the automaton step code section is clearly localized. With a separate function for it, we can better demonstrate this property:

#include 
enum states { before, inside, after };
void step(enum states *state, int c)
{
    if(c == '\n') {
        putchar('\n');
        *state = before;
    } else
    switch(*state) {
        case before:
            if(c != ' ') {
                putchar(c);
                *state = inside;
            }
            break;
        case inside:
            if(c == ' ') {
                *state = after;
            } else {
                putchar(c);
            }
            break;
        case after:
            break;
    }
} 
int main(void)
{
    int c;
    enum states state = before;
    while((c = getchar()) != EOF) {
        step(&state, c);
    }
    if(state != before)
        putchar('\n');
    return 0;
}

This example clearly demonstrates the basic properties of automata-based code:

1. time periods of automaton step executions may not overlap
2. the only information passed from the previous step to the next is the explicitly specified automaton state

Explicit state transition table

A finite automaton can be defined by an explicit state transition table. Generally speaking, an automata-based program code can naturally reflect this approach. In the program below there's an array named the_table, which defines the table. The rows of the table stand for three states, while columns reflect the input characters (first for spaces, second for the end of line character, and the last is for all the other characters).

For every possible combination, the table contains the new state number and the flag, which determines whether the automaton must print the symbol. In a real life task, this could be more complicated; e.g., the table could contain pointers to functions to be called on every possible combination of conditions.

#include 
enum states { before = 0, inside = 1, after = 2 };
struct branch {
    unsigned char new_state:2; //BIT [1:0]
    unsigned char should_putchar:1; //BIT [2]
};
struct branch the_table[3][3] = {
                 /* ' '         '\n'        others */
    /* before */ { {before,0}, {before,1}, {inside,1} },
    /* inside */ { {after, 1}, {before,1}, {inside,1} },
    /* after  */ { {after, 0}, {before,1}, {after, 0} }
};
void step(enum states *state, int c)
{
    int idx2 = (c == ' ') ? 0 : (c == '\n') ? 1 : 2;
    struct branch *b = & the_table[*state][idx2];
    *state = (enum states)(b->new_state);
    if(b->should_putchar) putchar(c);
}

Automation and Automata

Automata-based programming indeed closely matches the programming needs found in the field of automation.

A production cycle is commonly modeled as:

• A sequence of stages stepping according to input data (from captors).
• A set of actions performed depending on the current stage.

Various dedicated programming languages allow expressing such a model in more or less sophisticated ways.

Example Program

The example presented above could be expressed according to this view like in the following program. Here pseudo-code uses such conventions:

• 'set' and 'reset' respectively activate & inactivate a logic variable (here a stage)
• ':' is assignment, '=' is equality test

SPC : ' '
EOL : '\n'

states : (before, inside, after, end, endplusnl)

setState(c) {
    if c=EOF then if inside or after then set endplusnl else set end
    if before and (c!=SPC and c!=EOL) then set inside
    if inside and (c=SPC or c=EOL) then set after
    if after and c=EOL then set before
}

doAction(c) {
    if inside then write(c)
    else if c=EOL or endplusnl then write(EOL)
}

cycle {
    set before
    loop {
        c : readCharacter
        setState(c)
        doAction(c)
    }
    until end or endplusnl
}

The separation of routines expressing cycle progression on one side, and actual action on the other (matching input & output) allows clearer and simpler code.

Automation & Events

In the field of automation, stepping from step to step depends on input data coming from the machine itself. This is represented in the program by reading characters from a text. In reality, those data inform about position, speed, temperature, etc. of critical elements of a machine.

Like in GUI programming, changes in the machine state can thus be considered as events causing the passage from a state to another, until the final one is reached. The combination of possible states can generate a wide variety of events, thus defining a more complex production cycle. As a consequence, cycles are usually far to be simple linear sequences. There are commonly parallel branches running together and alternatives selected according to different events, schematically represented below:

   s:stage   c:condition
   
   s1
   |
   |-c2
   |
   s2
   |
   ----------
   |        |
   |-c31    |-c32
   |        |
  s31       s32
   |        |
   |-c41    |-c42
   |        |
   ----------
   |
   s4

Using object-oriented capabilities

If the implementation language supports object-oriented programming, a simple refactoring is to encapsulate the automaton into an object, thus hiding its implementation details. For example, an object-oriented version in C++ of the same program is below. A more sophisticated refactoring could employ the State pattern.

#include 
class StateMachine {
    enum states { before = 0, inside = 1, after = 2 } state;
    struct branch {
        unsigned char new_state:2;
        unsigned char should_putchar:1;
    };
    static struct branch the_table[3][3];
public:
    StateMachine() : state(before) {}
    void FeedChar(int c) {
        int idx2 = (c == ' ') ? 0 : (c == '\n') ? 1 : 2;
        struct branch *b = & the_table[state][idx2];
        state = (enum states)(b->new_state);
        if(b->should_putchar) putchar(c);
    }
};
struct StateMachine::branch StateMachine::the_table[3][3] = {
                 /* ' '         '\n'        others */
    /* before */ { {before,0}, {before,1}, {inside,1} },
    /* inside */ { {after, 0}, {before,1}, {inside,1} },
    /* after  */ { {after, 0}, {before,1}, {after, 0} }
};
int main(void)
{
    int c;
    StateMachine machine;
    while((c = getchar()) != EOF)
        machine.FeedChar(c);
    return 0;
}

Note: To minimize changes not directly related to the subject of the article, the input/output functions from the standard library of C are being used. Note the use of the ternary operator, which could also be implemented as if-else.

Applications

Automata-based programming is widely used in lexical and syntactic analyses.

Besides that, thinking in terms of automata (that is, breaking the execution process down to automaton steps and passing information from step to step through the explicit state) is necessary for event-driven programming as the only alternative to using parallel processes or threads.

The notions of states and state machines are often used in the field of formal specification. For instance, UML-based software architecture development uses state diagrams to specify the behaviour of the program. Also various communication protocols are often specified using the explicit notion of state.

Thinking in terms of automata (steps and states) can also be used to describe semantics of some programming languages. For example, the execution of a program written in the Refal language is described as a sequence of steps of a so-called abstract Refal machine; the state of the machine is a view (an arbitrary Refal expression without variables).

Continuations in the Scheme language require thinking in terms of steps and states, although Scheme itself is in no way automata-related (it is recursive). To make it possible the call/cc feature to work, implementation needs to be able to catch a whole state of the executing program, which is only possible when there's no implicit part in the state. Such a caught state is the very thing called continuation, and it can be considered as the state of a (relatively complicated) automaton. The step of the automaton is deducing the next continuation from the previous one, and the execution process is the cycle of such steps.

Alexander Ollongren in his book explains the so-called Vienna method of programming languages semantics description which is fully based on formal automata.

The STAT system  is a good example of using the automata-based approach; this system, besides other features, includes an embedded language called STATL which is purely automata-oriented.

History

Automata-based techniques were used widely in the domains where there are algorithms based on automata theory, such as formal language analyses.

One of the early papers on this is by Johnson et al., 1968.

One of the earliest mentions of automata-based programming as a general technique is found in the paper by Peter Naur, 1963. The author calls the technique Turing machine approach, however no real Turing machine is given in the paper; instead, the technique based on states and steps is described.

Compared against imperative and procedural programming

The notion of state is not exclusive property of automata-based programming. Generally speaking, state (or program state) appears during execution of any computer program, as a combination of all information that can change during the execution. For instance, a state of a traditional imperative program consists of

1. values of all variables and the information stored within dynamic memory
2. values stored in registers
3. stack contents (including local variables' values and return addresses)
4. current value of the instruction pointer

These can be divided to the explicit part (such as values stored in variables) and the implicit part (return addresses and the instruction pointer).

Having said this, an automata-based program can be considered as a special case of an imperative program, in which implicit part of the state is minimized. The state of the whole program taken at the two distinct moments of entering the step code section can differ in the automaton state only. This simplifies the analysis of the program.

Object-oriented programming relationship

In the theory of object-oriented programming an object is said to have an internal state and is capable of receiving messages, responding to them, sending messages to other objects and changing the internal state during message handling. In more practical terminology, to call an object's method is considered the same as to send a message to the object.

Thus, on the one hand, objects from object-oriented programming can be considered as automata (or models of automata) whose state is the combination of internal fields, and one or more methods are considered to be the step. Such methods must not call each other nor themselves, neither directly nor indirectly, otherwise the object can not be considered to be implemented in an automata-based manner.

On the other hand, object is good for implementing a model of an automaton. When the automata-based approach is used within an object-oriented language, an automaton model is usually implemented by a class, the state is represented with internal (private) fields of the class, and the step is implemented as a method; such a method is usually the only non-constant public method of the class (besides constructors and destructors). Other public methods could query the state but don't change it. All the secondary methods (such as particular state handlers) are usually hidden within the private part of the class.

Automata theory

From Wikipedia, the free encyclopedia

Classes of automata

(Clicking on each layer will take you to an article on that subject)

 

The study of the mathematical properties of such automata is automata theory. The picture is a visualization of an automaton that recognizes strings containing an even number of 0s. The automaton starts in state S1, and transitions to the non-accepting state S2 upon reading the symbol 0. Reading another 0 causes the automaton to transition back to the accepting state S1. In both states the symbol 1 is ignored by making a transition to the current state.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science and discrete mathematics (a subject of study in both mathematics and computer science). The word automata (the plural of automaton) comes from the Greek word αὐτόματα, which means "self-acting".

The figure above illustrates a finite-state machine, which belongs to a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the current state and the recent symbol as its inputs.

Automata theory is closely related to formal language theory. An automaton is a finite representation of a formal language that may be an infinite set. Automata are often classified by the class of formal languages they can recognize, typically illustrated by the Chomsky hierarchy, which describes the relations between various languages and kinds of formalized logic.

Automata play a major role in theory of computation, compiler construction, artificial intelligence, parsing and formal verification.

Automata

Following is an introductory definition of one type of automaton, which attempts to help one grasp the essential concepts involved in automata theory/theories.

Very informal description

An automaton is a construct made of states designed to determine if the input should be accepted or rejected. It looks a lot like a basic board game where each space on the board represents a state. Each state has information about what to do when an input is received by the machine (again, rather like what to do when you land on the Jail spot in a popular board game). As the machine receives a new input, it looks at the state and picks a new spot based on the information on what to do when it receives that input at that state. When there are no more inputs, the automaton stops and the space it is on when it completes determining whether the automaton accepts or rejects that particular set of inputs.

Informal description

An automaton runs when it is given some sequence of inputs in discrete (individual) time steps or steps. An automaton processes one input picked from a set of symbols or letters, which is called an alphabet. The symbols received by the automaton as input at any step are a finite sequence of symbols called words. An automaton has a finite set of states. At each moment during a run of the automaton, the automaton is in one of its states. When the automaton receives new input it moves to another state (or transitions) based on a function that takes the current state and symbol as parameters. This function is called the transition function. The automaton reads the symbols of the input word one after another and transitions from state to state according to the transition function until the word is read completely. Once the input word has been read, the automaton is said to have stopped. The state at which the automaton stops is called the final state. Depending on the final state, it's said that the automaton either accepts or rejects an input word. There is a subset of states of the automaton, which is defined as the set of accepting states. If the final state is an accepting state, then the automaton accepts the word. Otherwise, the word is rejected. The set of all the words accepted by an automaton is called the "language of that automaton". Any subset of the language of an automaton is a language recognized by that automaton.

In short, an automaton is a mathematical object that takes a word as input and decides whether to accept it or reject it. Since all computational problems are reducible into the accept/reject question on inputs, (all problem instances can be represented in a finite length of symbols)^{[citation needed]}, automata theory plays a crucial role in computational theory.

Formal definition

Definition of finite state automata

A deterministic finite automaton is represented formally by a 5-tuple Σ

, δ,q₀,F>, where:

• Q is a finite set of states.
• Σ is a finite set of symbols, called the alphabet of the automaton.
• δ is the transition function, that is, δ: Q × Σ → Q.
• q₀ is the start state, that is, the state of the automaton before any input has been processed, where q₀∈ Q.
• F is a set of states of Q (i.e. F⊆Q) called accept states.

Input word

An automaton reads a finite string of symbols a₁,a₂,...., a_n , where a_i ∈ Σ, which is called an input word. The set of all words is denoted by Σ*.

Run

A sequence of states q₀,q₁,q₂,...., q_n, where q_i ∈ Q such that q₀ is the start state and q_i = δ(q_i-1,a_i) for 0 < i ≤ n, is a run of the automaton on an input word w = a₁,a₂,...., a_n ∈ Σ*. In other words, at first the automaton is at the start state q₀, and then the automaton reads symbols of the input word in sequence. When the automaton reads symbol a_i it jumps to state q_i = δ(q_i-1,a_i). q_n is said to be the final state of the run.

Accepting word

A word w ∈ Σ* is accepted by the automaton if q_n ∈ F.

Recognized language

An automaton can recognize a formal language. The language L ⊆ Σ* recognized by an automaton is the set of all the words that are accepted by the automaton.

Recognizable languages

The recognizable languages are the set of languages that are recognized by some automaton. For the above definition of automata the recognizable languages are regular languages. For different definitions of automata, the recognizable languages are different.

Variant definitions of automata

Automata are defined to study useful machines under mathematical formalism. So, the definition of an automaton is open to variations according to the "real world machine", which we want to model using the automaton. People have studied many variations of automata. The most standard variant, which is described above, is called a deterministic finite automaton. The following are some popular variations in the definition of different components of automata.

Input

• Finite input: An automaton that accepts only finite sequence of symbols. The above introductory definition only encompasses finite words.
• Infinite input: An automaton that accepts infinite words (ω-words). Such automata are called ω-automata.
• Tree word input: The input may be a tree of symbols instead of sequence of symbols. In this case after reading each symbol, the automaton reads all the successor symbols in the input tree. It is said that the automaton makes one copy of itself for each successor and each such copy starts running on one of the successor symbols from the state according to the transition relation of the automaton. Such an automaton is called a tree automaton.
• Infinite tree input : The two extensions above can be combined, so the automaton reads a tree structure with (in)finite branches. Such an automaton is called an infinite tree automaton

States

• Finite states: An automaton that contains only a finite number of states. The above introductory definition describes automata with finite numbers of states.
• Infinite states: An automaton that may not have a finite number of states, or even a countable number of states. For example, the quantum finite automaton or topological automaton has uncountable infinity of states.
• Stack memory: An automaton may also contain some extra memory in the form of a stack in which symbols can be pushed and popped. This kind of automaton is called a pushdown automaton

Transition function

• Deterministic: For a given current state and an input symbol, if an automaton can only jump to one and only one state then it is a deterministic automaton.
• Nondeterministic: An automaton that, after reading an input symbol, may jump into any of a number of states, as licensed by its transition relation. Notice that the term transition function is replaced by transition relation: The automaton non-deterministically decides to jump into one of the allowed choices. Such automata are called nondeterministic automata.
• Alternation: This idea is quite similar to tree automaton, but orthogonal. The automaton may run its multiple copies on the same next read symbol. Such automata are called alternating automata. Acceptance condition must satisfy all runs of such copies to accept the input.

Acceptance condition

• Acceptance of finite words: Same as described in the informal definition above.
• Acceptance of infinite words: an omega automaton cannot have final states, as infinite words never terminate. Rather, acceptance of the word is decided by looking at the infinite sequence of visited states during the run.
• Probabilistic acceptance: An automaton need not strictly accept or reject an input. It may accept the input with some probability between zero and one. For example, quantum finite automaton, geometric automaton and metric automaton have probabilistic acceptance.

Different combinations of the above variations produce many classes of automaton.

Automata theory is a subject matter that studies properties of various types of automata. For example, the following questions are studied about a given type of automata.

• Which class of formal languages is recognizable by some type of automata? (Recognizable languages)
• Are certain automata closed under union, intersection, or complementation of formal languages? (Closure properties)
• How expressive is a type of automata in terms of recognizing a class of formal languages? And, their relative expressive power? (Language hierarchy)

Automata theory also studies the existence or nonexistence of any effective algorithms to solve problems similar to the following list:

• Does an automaton accept any input word? (Emptiness checking)
• Is it possible to transform a given non-deterministic automaton into deterministic automaton without changing the recognizable language? (Determinization)
• For a given formal language, what is the smallest automaton that recognizes it? (Minimization)

Classes of automata

The following is an incomplete list of types of automata.

Automaton	Recognizable language
Nondeterministic/Deterministic Finite state machine (FSM)	regular languages
Deterministic pushdown automaton (DPDA)	deterministic context-free languages
Pushdown automaton (PDA)	context-free languages
Linear bounded automaton (LBA)	context-sensitive languages
Turing machine	recursively enumerable languages
Deterministic Büchi automaton	ω-limit languages
Nondeterministic Büchi automaton	ω-regular languages
Rabin automaton, Streett automaton, Parity automaton, Muller automaton	ω-regular languages

Discrete, continuous, and hybrid automata

Normally automata theory describes the states of abstract machines but there are analog automata or continuous automata or hybrid discrete-continuous automata, which use analog data, continuous time, or both.

Hierarchy in terms of powers

The following is an incomplete hierarchy in terms of powers of different types of virtual machines. The hierarchy reflects the nested categories of languages the machines are able to accept.

Automaton

Deterministic Finite Automaton (DFA) -- Lowest Power (same power)    ${\displaystyle ||}$   (same power) Nondeterministic Finite Automaton (NFA) (above is weaker)    ${\displaystyle \cap }$    (below is stronger) Deterministic Push Down Automaton (DPDA-I) with 1 push-down store ${\displaystyle \cap }$ Nondeterministic Push Down Automaton (NPDA-I) with 1 push-down store ${\displaystyle \cap }$ Linear Bounded Automaton (LBA) ${\displaystyle \cap }$ Deterministic Push Down Automaton (DPDA-II) with 2 push-down stores ${\displaystyle ||}$ Nondeterministic Push Down Automaton (NPDA-II) with 2 push-down stores ${\displaystyle ||}$ Deterministic Turing Machine (DTM) ${\displaystyle ||}$ Nondeterministic Turing Machine (NTM) ${\displaystyle ||}$ Probabilistic Turing Machine (PTM) ${\displaystyle ||}$ Multitape Turing Machine (MTM) ${\displaystyle ||}$ Multidimensional Turing Machine

Applications

Each model in automata theory plays important roles in several applied areas. Finite automata are used in text processing, compilers, and hardware design. Context-free grammar (CFGs) are used in programming languages and artificial intelligence. Originally, CFGs were used in the study of the human languages. Cellular automata are used in the field of biology, the most common example being John Conway's Game of Life. Some other examples which could be explained using automata theory in biology include mollusk and pine cones growth and pigmentation patterns. Going further, a theory suggesting that the whole universe is computed by some sort of a discrete automaton, is advocated by some scientists. The idea originated in the work of Konrad Zuse, and was popularized in America by Edward Fredkin. Automata also appear in the theory of finite fields: the set of irreducible polynomials which can be written as composition of degree two polynomials is in fact a regular language.

Automata simulators

Automata simulators are pedagogical tools used to teach, learn and research automata theory. An automata simulator takes as input the description of an automaton and then simulates its working for an arbitrary input string. The description of the automaton can be entered in several ways. An automaton can be defined in a symbolic language or its specification may be entered in a predesigned form or its transition diagram may be drawn by clicking and dragging the mouse. Well known automata simulators include Turing's World, JFLAP, VAS, TAGS and SimStudio.

Connection to category theory

One can define several distinct categories of automata following the automata classification into different types described in the previous section. The mathematical category of deterministic automata, sequential machines or sequential automata, and Turing machines with automata homomorphisms defining the arrows between automata is a Cartesian closed category, it has both categorical limits and colimits. An automata homomorphism maps a quintuple of an automaton A_i onto the quintuple of another automaton A_j. Automata homomorphisms can also be considered as automata transformations or as semigroup homomorphisms, when the state space, S, of the automaton is defined as a semigroup S_g. Monoids are also considered as a suitable setting for automata in monoidal categories.

Categories of variable automata

One could also define a variable automaton, in the sense of Norbert Wiener in his book on The Human Use of Human Beings via the endomorphisms ${\displaystyle A_{i}\to A_{i}}$. Then, one can show that such variable automata homomorphisms form a mathematical group. In the case of non-deterministic, or other complex kinds of automata, the latter set of endomorphisms may become, however, a variable automaton groupoid. Therefore, in the most general case, categories of variable automata of any kind are categories of groupoids or groupoid categories. Moreover, the category of reversible automata is then a 2-category, and also a subcategory of the 2-category of groupoids, or the groupoid category.