Action potential

From Wikipedia, the free encyclopedia

As an action potential (nerve impulse) travels down an axon there is a change in polarity across the membrane of the axon. In response to a signal from another neuron, sodium- (Na⁺) and potassium- (K⁺) gated ion channels open and close as the membrane reaches its threshold potential. Na⁺ channels open at the beginning of the action potential, and Na⁺ moves into the axon, causing depolarization. Repolarization occurs when the K⁺ channels open and K⁺ moves out of the axon, creating a change in polarity between the outside of the cell and the inside. The impulse travels down the axon in one direction only, to the axon terminal where it signals other neurons.

In physiology, an action potential occurs when the membrane potential of a specific axon location rapidly rises and falls: this depolarisation then causes adjacent locations to similarly depolarise. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, endocrine cells, and in some plant cells.

In neurons, action potentials play a central role in cell-to-cell communication by providing for—or, with regard to saltatory conduction, assisting—the propagation of signals along the neuron's axon towards synaptic boutons situated at the ends of an axon; these signals can then connect with other neurons at synapses, or to motor cells or glands. In other types of cells, their main function is to activate intracellular processes. In muscle cells, for example, an action potential is the first step in the chain of events leading to contraction. In beta cells of the pancreas, they provoke release of insulin. Action potentials in neurons are also known as "nerve impulses" or "spikes", and the temporal sequence of action potentials generated by a neuron is called its "spike train". A neuron that emits an action potential, or nerve impulse, is often said to "fire".

Action potentials are generated by special types of voltage-gated ion channels embedded in a cell's plasma membrane. These channels are shut when the membrane potential is near the (negative) resting potential of the cell, but they rapidly begin to open if the membrane potential increases to a precisely defined threshold voltage, depolarising the transmembrane potential. When the channels open, they allow an inward flow of sodium ions, which changes the electrochemical gradient, which in turn produces a further rise in the membrane potential. This then causes more channels to open, producing a greater electric current across the cell membrane, and so on. The process proceeds explosively until all of the available ion channels are open, resulting in a large upswing in the membrane potential. The rapid influx of sodium ions causes the polarity of the plasma membrane to reverse, and the ion channels then rapidly inactivate. As the sodium channels close, sodium ions can no longer enter the neuron, and then they are actively transported back out of the plasma membrane. Potassium channels are then activated, and there is an outward current of potassium ions, returning the electrochemical gradient to the resting state. After an action potential has occurred, there is a transient negative shift, called the afterhyperpolarization. 

In animal cells, there are two primary types of action potentials. One type is generated by voltage-gated sodium channels, the other by voltage-gated calcium channels. Sodium-based action potentials usually last for under one millisecond, but calcium-based action potentials may last for 100 milliseconds or longer. In some types of neurons, slow calcium spikes provide the driving force for a long burst of rapidly emitted sodium spikes. In cardiac muscle cells, on the other hand, an initial fast sodium spike provides a "primer" to provoke the rapid onset of a calcium spike, which then produces muscle contraction.

In the Hodgkin–Huxley membrane capacitance model, the speed of transmission of an action potential was undefined and it was assumed that adjacent areas became depolarized due to released ion interference with neighboring channels. Measurements of ion diffusion and radii have since shown this not to be possible. Moreover, contradictory measurements of entropy changes and timing disputed the capacitance model as acting alone.

Overview

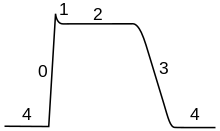
Shape of a typical action potential. The membrane potential remains near a baseline level until at some point in time, it abruptly spikes upward and then rapidly falls.

 

Nearly all cell membranes in animals, plants and fungi maintain a voltage difference between the exterior and interior of the cell, called the membrane potential. A typical voltage across an animal cell membrane is −70 mV. This means that the interior of the cell has a negative voltage of approximately one-fifteenth of a volt relative to the exterior. In most types of cells, the membrane potential usually stays fairly constant. Some types of cells, however, are electrically active in the sense that their voltages fluctuate over time. In some types of electrically active cells, including neurons and muscle cells, the voltage fluctuations frequently take the form of a rapid upward spike followed by a rapid fall. These up-and-down cycles are known as action potentials. In some types of neurons, the entire up-and-down cycle takes place in a few thousandths of a second. In muscle cells, a typical action potential lasts about a fifth of a second. In some other types of cells, and also in plants, an action potential may last three seconds or more.

The electrical properties of a cell are determined by the structure of the membrane that surrounds it. A cell membrane consists of a lipid bilayer of molecules in which larger protein molecules are embedded. The lipid bilayer is highly resistant to movement of electrically charged ions, so it functions as an insulator. The large membrane-embedded proteins, in contrast, provide channels through which ions can pass across the membrane. Action potentials are driven by channel proteins whose configuration switches between closed and open states as a function of the voltage difference between the interior and exterior of the cell. These voltage-sensitive proteins are known as voltage-gated ion channels. 

An in-depth process of how an action potential will pass through a neuron during neuron transmission including the 4 stages: resting potential, depolarization, re-polarization, and back to resting potential. The diagram shows how sodium ions and potassium ions interact to show how the changing of charge allows the action potential to cross with the use of facilitated diffusion and active transport.

Process in a typical neuron

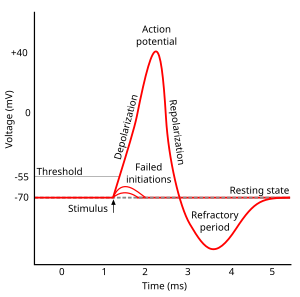
Approximate plot of a typical action potential shows its various phases as the action potential passes a point on a cell membrane. The membrane potential starts out at −70 mV at time zero. A stimulus is applied at time = 1 ms, which raises the membrane potential above −55 mV (the threshold potential). After the stimulus is applied, the membrane potential rapidly rises to a peak potential of +40 mV at time = 2 ms. Just as quickly, the potential then drops and overshoots to −90 mV at time = 3 ms, and finally the resting potential of −70 mV is reestablished at time = 5 ms.

 

All cells in animal body tissues are electrically polarized – in other words, they maintain a voltage difference across the cell's plasma membrane, known as the membrane potential. This electrical polarization results from a complex interplay between protein structures embedded in the membrane called ion pumps and ion channels. In neurons, the types of ion channels in the membrane usually vary across different parts of the cell, giving the dendrites, axon, and cell body different electrical properties. As a result, some parts of the membrane of a neuron may be excitable (capable of generating action potentials), whereas others are not. Recent studies have shown that the most excitable part of a neuron is the part after the axon hillock (the point where the axon leaves the cell body), which is called the initial segment, but the axon and cell body are also excitable in most cases.

Each excitable patch of membrane has two important levels of membrane potential: the resting potential, which is the value the membrane potential maintains as long as nothing perturbs the cell, and a higher value called the threshold potential. At the axon hillock of a typical neuron, the resting potential is around –70 millivolts (mV) and the threshold potential is around –55 mV. Synaptic inputs to a neuron cause the membrane to depolarize or hyperpolarize; that is, they cause the membrane potential to rise or fall. Action potentials are triggered when enough depolarization accumulates to bring the membrane potential up to threshold. When an action potential is triggered, the membrane potential abruptly shoots upward and then equally abruptly shoots back downward, often ending below the resting level, where it remains for some period of time. The shape of the action potential is stereotyped; this means that the rise and fall usually have approximately the same amplitude and time course for all action potentials in a given cell. (Exceptions are discussed later in the article). In most neurons, the entire process takes place in about a thousandth of a second. Many types of neurons emit action potentials constantly at rates of up to 10–100 per second. However, some types are much quieter, and may go for minutes or longer without emitting any action potentials.

Biophysical basis

Action potentials result from the presence in a cell's membrane of special types of voltage-gated ion channels. A voltage-gated ion channel is a cluster of proteins embedded in the membrane that has three key properties:

1. It is capable of assuming more than one conformation.
2. At least one of the conformations creates a channel through the membrane that is permeable to specific types of ions.
3. The transition between conformations is influenced by the membrane potential.

Thus, a voltage-gated ion channel tends to be open for some values of the membrane potential, and closed for others. In most cases, however, the relationship between membrane potential and channel state is probabilistic and involves a time delay. Ion channels switch between conformations at unpredictable times: The membrane potential determines the rate of transitions and the probability per unit time of each type of transition. 

Action potential propagation along an axon

Voltage-gated ion channels are capable of producing action potentials because they can give rise to positive feedback loops: The membrane potential controls the state of the ion channels, but the state of the ion channels controls the membrane potential. Thus, in some situations, a rise in the membrane potential can cause ion channels to open, thereby causing a further rise in the membrane potential. An action potential occurs when this positive feedback cycle proceeds explosively. The time and amplitude trajectory of the action potential are determined by the biophysical properties of the voltage-gated ion channels that produce it. Several types of channels capable of producing the positive feedback necessary to generate an action potential do exist. Voltage-gated sodium channels are responsible for the fast action potentials involved in nerve conduction. Slower action potentials in muscle cells and some types of neurons are generated by voltage-gated calcium channels. Each of these types comes in multiple variants, with different voltage sensitivity and different temporal dynamics.

The most intensively studied type of voltage-dependent ion channels comprises the sodium channels involved in fast nerve conduction. These are sometimes known as Hodgkin-Huxley sodium channels because they were first characterized by Alan Hodgkin and Andrew Huxley in their Nobel Prize-winning studies of the biophysics of the action potential, but can more conveniently be referred to as Na_V channels. (The "V" stands for "voltage".) An Na_V channel has three possible states, known as deactivated, activated, and inactivated. The channel is permeable only to sodium ions when it is in the activated state. When the membrane potential is low, the channel spends most of its time in the deactivated (closed) state. If the membrane potential is raised above a certain level, the channel shows increased probability of transitioning to the activated (open) state. The higher the membrane potential the greater the probability of activation. Once a channel has activated, it will eventually transition to the inactivated (closed) state. It tends then to stay inactivated for some time, but, if the membrane potential becomes low again, the channel will eventually transition back to the deactivated state. During an action potential, most channels of this type go through a cycle deactivated→activated→inactivated→deactivated. This is only the population average behavior, however — an individual channel can in principle make any transition at any time. However, the likelihood of a channel's transitioning from the inactivated state directly to the activated state is very low: A channel in the inactivated state is refractory until it has transitioned back to the deactivated state. 

The outcome of all this is that the kinetics of the Na_V channels are governed by a transition matrix whose rates are voltage-dependent in a complicated way. Since these channels themselves play a major role in determining the voltage, the global dynamics of the system can be quite difficult to work out. Hodgkin and Huxley approached the problem by developing a set of differential equations for the parameters that govern the ion channel states, known as the Hodgkin-Huxley equations. These equations have been extensively modified by later research, but form the starting point for most theoretical studies of action potential biophysics.

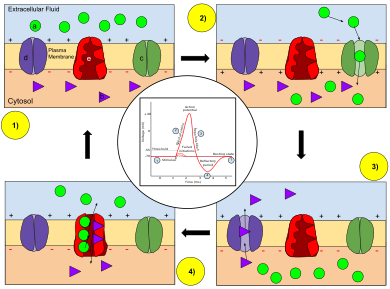
Ion movement during an action potential.
Key: a) Sodium (Na⁺) ion. b) Potassium (K⁺) ion. c) Sodium channel. d) Potassium channel. e) Sodium-potassium pump.
In the stages of an action potential, the permeability of the membrane of the neuron changes. At the resting state (1), sodium and potassium ions are unable to pass through the membrane, and the neuron has a negative charge inside (mainly due to the large proteins that are negatively charged). Once the action potential is triggered, the depolarization (2) of the neuron activates the sodium channel, allowing sodium ions to pass through the membrane of the neuron and results in a positive charge in the neuron and a negative charge in the extracellular fluid. After the action potential is reached, the neuron begins repolarization (3), where the sodium channels close and the potassium channels open, allowing potassium ions to cross the membrane and flood into the extracellular fluid, resulting in a positive charge in the extracellular fluid and a negative charge that is below the resting potential of the neuron. Finally, to return the neuron to that resting potential after the potassium pump closes, a sodium-potassium pump works to exchange three sodium ions per two potassium ions across the plasma membrane during the refractory period (4). Once the Na⁺ and K⁺ are back where they started, the neuron is back to its resting state (1), ready to repeat the process for the next action potential.

 

As the membrane potential is increased, sodium ion channels open, allowing the entry of sodium ions into the cell. This is followed by the opening of potassium ion channels that permit the exit of potassium ions from the cell. The inward flow of sodium ions increases the concentration of positively charged cations in the cell and causes depolarization, where the potential of the cell is higher than the cell's resting potential. The sodium channels close at the peak of the action potential, while potassium continues to leave the cell. The efflux of potassium ions decreases the membrane potential or hyperpolarizes the cell. For small voltage increases from rest, the potassium current exceeds the sodium current and the voltage returns to its normal resting value, typically −70 mV. However, if the voltage increases past a critical threshold, typically 15 mV higher than the resting value, the sodium current dominates. This results in a runaway condition whereby the positive feedback from the sodium current activates even more sodium channels. Thus, the cell fires, producing an action potential. The frequency at which a neuron elicits action potentials is often referred to as a firing rate or neural firing rate. 

Currents produced by the opening of voltage-gated channels in the course of an action potential are typically significantly larger than the initial stimulating current. Thus, the amplitude, duration, and shape of the action potential are determined largely by the properties of the excitable membrane and not the amplitude or duration of the stimulus. This all-or-nothing property of the action potential sets it apart from graded potentials such as receptor potentials, electrotonic potentials, and synaptic potentials, which scale with the magnitude of the stimulus. A variety of action potential types exist in many cell types and cell compartments as determined by the types of voltage-gated channels, leak channels, channel distributions, ionic concentrations, membrane capacitance, temperature, and other factors. 

The principal ions involved in an action potential are sodium and potassium cations; sodium ions enter the cell, and potassium ions leave, restoring equilibrium. Relatively few ions need to cross the membrane for the membrane voltage to change drastically. The ions exchanged during an action potential, therefore, make a negligible change in the interior and exterior ionic concentrations. The few ions that do cross are pumped out again by the continuous action of the sodium–potassium pump, which, with other ion transporters, maintains the normal ratio of ion concentrations across the membrane. Calcium cations and chloride anions are involved in a few types of action potentials, such as the cardiac action potential and the action potential in the single-cell alga Acetabularia, respectively. 

Although action potentials are generated locally on patches of excitable membrane, the resulting currents can trigger action potentials on neighboring stretches of membrane, precipitating a domino-like propagation. In contrast to passive spread of electric potentials (electrotonic potential), action potentials are generated anew along excitable stretches of membrane and propagate without decay. Myelinated sections of axons are not excitable and do not produce action potentials and the signal is propagated passively as electrotonic potential. Regularly spaced unmyelinated patches, called the nodes of Ranvier, generate action potentials to boost the signal. Known as saltatory conduction, this type of signal propagation provides a favorable tradeoff of signal velocity and axon diameter. Depolarization of axon terminals, in general, triggers the release of neurotransmitter into the synaptic cleft. In addition, backpropagating action potentials have been recorded in the dendrites of pyramidal neurons, which are ubiquitous in the neocortex. These are thought to have a role in spike-timing-dependent plasticity.

Maturation of the electrical properties of the action potential

A neuron's ability to generate and propagate an action potential changes during development. How much the membrane potential of a neuron changes as the result of a current impulse is a function of the membrane input resistance. As a cell grows, more channels are added to the membrane, causing a decrease in input resistance. A mature neuron also undergoes shorter changes in membrane potential in response to synaptic currents. Neurons from a ferret lateral geniculate nucleus have a longer time constant and larger voltage deflection at P0 than they do at P30. One consequence of the decreasing action potential duration is that the fidelity of the signal can be preserved in response to high frequency stimulation. Immature neurons are more prone to synaptic depression than potentiation after high frequency stimulation.

In the early development of many organisms, the action potential is actually initially carried by calcium current rather than sodium current. The opening and closing kinetics of calcium channels during development are slower than those of the voltage-gated sodium channels that will carry the action potential in the mature neurons. The longer opening times for the calcium channels can lead to action potentials that are considerably slower than those of mature neurons. Xenopus neurons initially have action potentials that take 60–90 ms. During development, this time decreases to 1 ms. There are two reasons for this drastic decrease. First, the inward current becomes primarily carried by sodium channels. Second, the delayed rectifier, a potassium channel current, increases to 3.5 times its initial strength.

In order for the transition from a calcium-dependent action potential to a sodium-dependent action potential to proceed new channels must be added to the membrane. If Xenopus neurons are grown in an environment with RNA synthesis or protein synthesis inhibitors that transition is prevented. Even the electrical activity of the cell itself may play a role in channel expression. If action potentials in Xenopus myocytes are blocked, the typical increase in sodium and potassium current density is prevented or delayed.

This maturation of electrical properties is seen across species. Xenopus sodium and potassium currents increase drastically after a neuron goes through its final phase of mitosis. The sodium current density of rat cortical neurons increases by 600% within the first two postnatal weeks.

Neurotransmission

Anatomy of a neuron

Structure of a typical neuron

Neuron
Dendrite Soma Axon Nucleus Node of Ranvier Axon terminal Schwann cell Myelin sheath

Several types of cells support an action potential, such as plant cells, muscle cells, and the specialized cells of the heart (in which occurs the cardiac action potential). However, the main excitable cell is the neuron, which also has the simplest mechanism for the action potential.

Neurons are electrically excitable cells composed, in general, of one or more dendrites, a single soma, a single axon and one or more axon terminals. Dendrites are cellular projections whose primary function is to receive synaptic signals. Their protrusions, known as dendritic spines, are designed to capture the neurotransmitters released by the presynaptic neuron. They have a high concentration of ligand-gated ion channels. These spines have a thin neck connecting a bulbous protrusion to the dendrite. This ensures that changes occurring inside the spine are less likely to affect the neighboring spines. The dendritic spine can, with rare exception, act as an independent unit. The dendrites extend from the soma, which houses the nucleus, and many of the "normal" eukaryotic organelles. Unlike the spines, the surface of the soma is populated by voltage activated ion channels. These channels help transmit the signals generated by the dendrites. Emerging out from the soma is the axon hillock. This region is characterized by having a very high concentration of voltage-activated sodium channels. In general, it is considered to be the spike initiation zone for action potentials,^[14] i.e. the trigger zone. Multiple signals generated at the spines, and transmitted by the soma all converge here. Immediately after the axon hillock is the axon. This is a thin tubular protrusion traveling away from the soma. The axon is insulated by a myelin sheath. Myelin is composed of either Schwann cells (in the peripheral nervous system) or oligodendrocytes (in the central nervous system), both of which are types of glial cells. Although glial cells are not involved with the transmission of electrical signals, they communicate and provide important biochemical support to neurons. To be specific, myelin wraps multiple times around the axonal segment, forming a thick fatty layer that prevents ions from entering or escaping the axon. This insulation prevents significant signal decay as well as ensuring faster signal speed. This insulation, however, has the restriction that no channels can be present on the surface of the axon. There are, therefore, regularly spaced patches of membrane, which have no insulation. These nodes of Ranvier can be considered to be "mini axon hillocks", as their purpose is to boost the signal in order to prevent significant signal decay. At the furthest end, the axon loses its insulation and begins to branch into several axon terminals. These presynaptic terminals, or synaptic boutons, are a specialized area within the axon of the presynaptic cell that contains neurotransmitters enclosed in small membrane-bound spheres called synaptic vesicles.

Initiation

Before considering the propagation of action potentials along axons and their termination at the synaptic knobs, it is helpful to consider the methods by which action potentials can be initiated at the axon hillock. The basic requirement is that the membrane voltage at the hillock be raised above the threshold for firing. There are several ways in which this depolarization can occur. 

When an action potential arrives at the end of the pre-synaptic axon (top), it causes the release of neurotransmitter molecules that open ion channels in the post-synaptic neuron (bottom). The combined excitatory and inhibitory postsynaptic potentials of such inputs can begin a new action potential in the post-synaptic neuron.

Dynamics

Action potentials are most commonly initiated by excitatory postsynaptic potentials from a presynaptic neuron. Typically, neurotransmitter molecules are released by the presynaptic neuron. These neurotransmitters then bind to receptors on the postsynaptic cell. This binding opens various types of ion channels. This opening has the further effect of changing the local permeability of the cell membrane and, thus, the membrane potential. If the binding increases the voltage (depolarizes the membrane), the synapse is excitatory. If, however, the binding decreases the voltage (hyperpolarizes the membrane), it is inhibitory. Whether the voltage is increased or decreased, the change propagates passively to nearby regions of the membrane (as described by the cable equation and its refinements). Typically, the voltage stimulus decays exponentially with the distance from the synapse and with time from the binding of the neurotransmitter. Some fraction of an excitatory voltage may reach the axon hillock and may (in rare cases) depolarize the membrane enough to provoke a new action potential. More typically, the excitatory potentials from several synapses must work together at nearly the same time to provoke a new action potential. Their joint efforts can be thwarted, however, by the counteracting inhibitory postsynaptic potentials. 

Neurotransmission can also occur through electrical synapses. Due to the direct connection between excitable cells in the form of gap junctions, an action potential can be transmitted directly from one cell to the next in either direction. The free flow of ions between cells enables rapid non-chemical-mediated transmission. Rectifying channels ensure that action potentials move only in one direction through an electrical synapse. Electrical synapses are found in all nervous systems, including the human brain, although they are a distinct minority.

"All-or-none" principle

The amplitude of an action potential is independent of the amount of current that produced it. In other words, larger currents do not create larger action potentials. Therefore, action potentials are said to be all-or-none signals, since either they occur fully or they do not occur at all. This is in contrast to receptor potentials, whose amplitudes are dependent on the intensity of a stimulus. In both cases, the frequency of action potentials is correlated with the intensity of a stimulus.

Sensory neurons

In sensory neurons, an external signal such as pressure, temperature, light, or sound is coupled with the opening and closing of ion channels, which in turn alter the ionic permeabilities of the membrane and its voltage. These voltage changes can again be excitatory (depolarizing) or inhibitory (hyperpolarizing) and, in some sensory neurons, their combined effects can depolarize the axon hillock enough to provoke action potentials. Some examples in humans include the olfactory receptor neuron and Meissner's corpuscle, which are critical for the sense of smell and touch, respectively. However, not all sensory neurons convert their external signals into action potentials; some do not even have an axon. Instead, they may convert the signal into the release of a neurotransmitter, or into continuous graded potentials, either of which may stimulate subsequent neuron(s) into firing an action potential. For illustration, in the human ear, hair cells convert the incoming sound into the opening and closing of mechanically gated ion channels, which may cause neurotransmitter molecules to be released. In similar manner, in the human retina, the initial photoreceptor cells and the next layer of cells (comprising bipolar cells and horizontal cells) do not produce action potentials; only some amacrine cells and the third layer, the ganglion cells, produce action potentials, which then travel up the optic nerve.

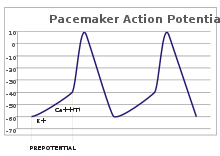
Pacemaker potentials

In pacemaker potentials, the cell spontaneously depolarizes (straight line with upward slope) until it fires an action potential.

 

In sensory neurons, action potentials result from an external stimulus. However, some excitable cells require no such stimulus to fire: They spontaneously depolarize their axon hillock and fire action potentials at a regular rate, like an internal clock. The voltage traces of such cells are known as pacemaker potentials. The cardiac pacemaker cells of the sinoatrial node in the heart provide a good example. Although such pacemaker potentials have a natural rhythm, it can be adjusted by external stimuli; for instance, heart rate can be altered by pharmaceuticals as well as signals from the sympathetic and parasympathetic nerves. The external stimuli do not cause the cell's repetitive firing, but merely alter its timing. In some cases, the regulation of frequency can be more complex, leading to patterns of action potentials, such as bursting.

Phases

The course of the action potential can be divided into five parts: the rising phase, the peak phase, the falling phase, the undershoot phase, and the refractory period. During the rising phase the membrane potential depolarizes (becomes more positive). The point at which depolarization stops is called the peak phase. At this stage, the membrane potential reaches a maximum. Subsequent to this, there is a falling phase. During this stage the membrane potential becomes more negative, returning towards resting potential. The undershoot, or after hyperpolarization, phase is the period during which the membrane potential temporarily becomes more negatively charged than when at rest (hyperpolarized). Finally, the time during which a subsequent action potential is impossible or difficult to fire is called the refractory period, which may overlap with the other phases.

The course of the action potential is determined by two coupled effects. First, voltage-sensitive ion channels open and close in response to changes in the membrane voltage V_m. This changes the membrane's permeability to those ions. Second, according to the Goldman equation, this change in permeability changes the equilibrium potential E_m, and, thus, the membrane voltage V_m. Thus, the membrane potential affects the permeability, which then further affects the membrane potential. This sets up the possibility for positive feedback, which is a key part of the rising phase of the action potential. A complicating factor is that a single ion channel may have multiple internal "gates" that respond to changes in V_m in opposite ways, or at different rates. For example, although raising V_m opens most gates in the voltage-sensitive sodium channel, it also closes the channel's "inactivation gate", albeit more slowly. Hence, when V_m is raised suddenly, the sodium channels open initially, but then close due to the slower inactivation.

The voltages and currents of the action potential in all of its phases were modeled accurately by Alan Lloyd Hodgkin and Andrew Huxley in 1952, for which they were awarded the Nobel Prize in Physiology or Medicine in 1963. However, their model considers only two types of voltage-sensitive ion channels, and makes several assumptions about them, e.g., that their internal gates open and close independently of one another. In reality, there are many types of ion channels, and they do not always open and close independently.

Stimulation and rising phase

A typical action potential begins at the axon hillock with a sufficiently strong depolarization, e.g., a stimulus that increases V_m. This depolarization is often caused by the injection of extra sodium cations into the cell; these cations can come from a wide variety of sources, such as chemical synapses, sensory neurons or pacemaker potentials.

For a neuron at rest, there is a high concentration of sodium and chloride ions in the extracellular fluid compared to the intracellular fluid while there is a high concentration of potassium ions in the intracellular fluid compared to the extracellular fluid. This concentration gradient along with potassium leak channels present on the membrane of the neuron causes an efflux of potassium ions making the resting potential close to E_K ≈ –75 mV. The depolarization opens both the sodium and potassium channels in the membrane, allowing the ions to flow into and out of the axon, respectively. If the depolarization is small (say, increasing V_m from −70 mV to −60 mV), the outward potassium current overwhelms the inward sodium current and the membrane repolarizes back to its normal resting potential around −70 mV. However, if the depolarization is large enough, the inward sodium current increases more than the outward potassium current and a runaway condition (positive feedback) results: the more inward current there is, the more V_m increases, which in turn further increases the inward current. A sufficiently strong depolarization (increase in V_m) causes the voltage-sensitive sodium channels to open; the increasing permeability to sodium drives V_m closer to the sodium equilibrium voltage E_Na≈ +55 mV. The increasing voltage in turn causes even more sodium channels to open, which pushes V_m still further towards E_Na. This positive feedback continues until the sodium channels are fully open and V_m is close to E_Na. The sharp rise in V_m and sodium permeability correspond to the rising phase of the action potential.

The critical threshold voltage for this runaway condition is usually around −45 mV, but it depends on the recent activity of the axon. A membrane that has just fired an action potential cannot fire another one immediately, since the ion channels have not returned to the deactivated state. The period during which no new action potential can be fired is called the absolute refractory period. At longer times, after some but not all of the ion channels have recovered, the axon can be stimulated to produce another action potential, but with a higher threshold, requiring a much stronger depolarization, e.g., to −30 mV. The period during which action potentials are unusually difficult to evoke is called the relative refractory period.

Peak and falling phase

The positive feedback of the rising phase slows and comes to a halt as the sodium ion channels become maximally open. At the peak of the action potential, the sodium permeability is maximized and the membrane voltage V_m is nearly equal to the sodium equilibrium voltage E_Na. However, the same raised voltage that opened the sodium channels initially also slowly shuts them off, by closing their pores; the sodium channels become inactivated. This lowers the membrane's permeability to sodium relative to potassium, driving the membrane voltage back towards the resting value. At the same time, the raised voltage opens voltage-sensitive potassium channels; the increase in the membrane's potassium permeability drives V_m towards E_K. Combined, these changes in sodium and potassium permeability cause V_m to drop quickly, repolarizing the membrane and producing the "falling phase" of the action potential.

After hyperpolarization

The raised voltage opened many more potassium channels than usual, and some of these do not close right away when the membrane returns to its normal resting voltage. In addition, further potassium channels open in response to the influx of calcium ions during the action potential. The potassium permeability of the membrane is transiently unusually high, driving the membrane voltage V_m even closer to the potassium equilibrium voltage E_K. Hence, there is an undershoot or hyperpolarization, termed an afterhyperpolarization in technical language, that persists until the membrane potassium permeability returns to its usual value.

Refractory period

Each action potential is followed by a refractory period, which can be divided into an absolute refractory period, during which it is impossible to evoke another action potential, and then a relative refractory period, during which a stronger-than-usual stimulus is required. These two refractory periods are caused by changes in the state of sodium and potassium channel molecules. When closing after an action potential, sodium channels enter an "inactivated" state, in which they cannot be made to open regardless of the membrane potential—this gives rise to the absolute refractory period. Even after a sufficient number of sodium channels have transitioned back to their resting state, it frequently happens that a fraction of potassium channels remains open, making it difficult for the membrane potential to depolarize, and thereby giving rise to the relative refractory period. Because the density and sub-types of potassium channels may differ greatly between different types of neurons, the duration of the relative refractory period is highly variable.

The absolute refractory period is largely responsible for the unidirectional propagation of action potentials along axons. At any given moment, the patch of axon behind the actively spiking part is refractory, but the patch in front, not having been activated recently, is capable of being stimulated by the depolarization from the action potential.

Propagation

The action potential generated at the axon hillock propagates as a wave along the axon. The currents flowing inwards at a point on the axon during an action potential spread out along the axon, and depolarize the adjacent sections of its membrane. If sufficiently strong, this depolarization provokes a similar action potential at the neighboring membrane patches. This basic mechanism was demonstrated by Alan Lloyd Hodgkin in 1937. After crushing or cooling nerve segments and thus blocking the action potentials, he showed that an action potential arriving on one side of the block could provoke another action potential on the other, provided that the blocked segment was sufficiently short.

Once an action potential has occurred at a patch of membrane, the membrane patch needs time to recover before it can fire again. At the molecular level, this absolute refractory period corresponds to the time required for the voltage-activated sodium channels to recover from inactivation, i.e., to return to their closed state. There are many types of voltage-activated potassium channels in neurons. Some of them inactivate fast (A-type currents) and some of them inactivate slowly or not inactivate at all; this variability guarantees that there will be always an available source of current for repolarization, even if some of the potassium channels are inactivated because of preceding depolarization. On the other hand, all neuronal voltage-activated sodium channels inactivate within several milliseconds during strong depolarization, thus making following depolarization impossible until a substantial fraction of sodium channels have returned to their closed state. Although it limits the frequency of firing, the absolute refractory period ensures that the action potential moves in only one direction along an axon. The currents flowing in due to an action potential spread out in both directions along the axon. However, only the unfired part of the axon can respond with an action potential; the part that has just fired is unresponsive until the action potential is safely out of range and cannot restimulate that part. In the usual orthodromic conduction, the action potential propagates from the axon hillock towards the synaptic knobs (the axonal termini); propagation in the opposite direction—known as antidromic conduction—is very rare. However, if a laboratory axon is stimulated in its middle, both halves of the axon are "fresh", i.e., unfired; then two action potentials will be generated, one traveling towards the axon hillock and the other traveling towards the synaptic knobs.

Myelin and saltatory conduction

In saltatory conduction, an action potential at one node of Ranvier causes inwards currents that depolarize the membrane at the next node, provoking a new action potential there; the action potential appears to "hop" from node to node.

 

In order to enable fast and efficient transduction of electrical signals in the nervous system, certain neuronal axons are covered with myelin sheaths. Myelin is a multilamellar membrane that enwraps the axon in segments separated by intervals known as nodes of Ranvier. It is produced by specialized cells: Schwann cells exclusively in the peripheral nervous system, and oligodendrocytes exclusively in the central nervous system. Myelin sheath reduces membrane capacitance and increases membrane resistance in the inter-node intervals, thus allowing a fast, saltatory movement of action potentials from node to node. Myelination is found mainly in vertebrates, but an analogous system has been discovered in a few invertebrates, such as some species of shrimp. Not all neurons in vertebrates are myelinated; for example, axons of the neurons comprising the autonomous nervous system are not, in general, myelinated. 

Myelin prevents ions from entering or leaving the axon along myelinated segments. As a general rule, myelination increases the conduction velocity of action potentials and makes them more energy-efficient. Whether saltatory or not, the mean conduction velocity of an action potential ranges from 1 meter per second (m/s) to over 100 m/s, and, in general, increases with axonal diameter.

Action potentials cannot propagate through the membrane in myelinated segments of the axon. However, the current is carried by the cytoplasm, which is sufficient to depolarize the first or second subsequent node of Ranvier. Instead, the ionic current from an action potential at one node of Ranvier provokes another action potential at the next node; this apparent "hopping" of the action potential from node to node is known as saltatory conduction. Although the mechanism of saltatory conduction was suggested in 1925 by Ralph Lillie, the first experimental evidence for saltatory conduction came from Ichiji Tasaki and Taiji Takeuchi and from Andrew Huxley and Robert Stämpfli. By contrast, in unmyelinated axons, the action potential provokes another in the membrane immediately adjacent, and moves continuously down the axon like a wave. 

Comparison of the conduction velocities of myelinated and unmyelinated axons in the cat. The conduction velocity v of myelinated neurons varies roughly linearly with axon diameter d (that is, v ∝ d), whereas the speed of unmyelinated neurons varies roughly as the square root (v ∝√d). The red and blue curves are fits of experimental data, whereas the dotted lines are their theoretical extrapolations.

 

Myelin has two important advantages: fast conduction speed and energy efficiency. For axons larger than a minimum diameter (roughly 1 micrometre), myelination increases the conduction velocity of an action potential, typically tenfold. Conversely, for a given conduction velocity, myelinated fibers are smaller than their unmyelinated counterparts. For example, action potentials move at roughly the same speed (25 m/s) in a myelinated frog axon and an unmyelinated squid giant axon, but the frog axon has a roughly 30-fold smaller diameter and 1000-fold smaller cross-sectional area. Also, since the ionic currents are confined to the nodes of Ranvier, far fewer ions "leak" across the membrane, saving metabolic energy. This saving is a significant selective advantage, since the human nervous system uses approximately 20% of the body's metabolic energy.

The length of axons' myelinated segments is important to the success of saltatory conduction. They should be as long as possible to maximize the speed of conduction, but not so long that the arriving signal is too weak to provoke an action potential at the next node of Ranvier. In nature, myelinated segments are generally long enough for the passively propagated signal to travel for at least two nodes while retaining enough amplitude to fire an action potential at the second or third node. Thus, the safety factor of saltatory conduction is high, allowing transmission to bypass nodes in case of injury. However, action potentials may end prematurely in certain places where the safety factor is low, even in unmyelinated neurons; a common example is the branch point of an axon, where it divides into two axons.

Some diseases degrade myelin and impair saltatory conduction, reducing the conduction velocity of action potentials. The most well-known of these is multiple sclerosis, in which the breakdown of myelin impairs coordinated movement.

Cable theory

Cable theory's simplified view of a neuronal fiber. The connected RC circuits correspond to adjacent segments of a passive neurite. The extracellular resistances r_e (the counterparts of the intracellular resistances r_i) are not shown, since they are usually negligibly small; the extracellular medium may be assumed to have the same voltage everywhere.

 

The flow of currents within an axon can be described quantitatively by cable theory and its elaborations, such as the compartmental model. Cable theory was developed in 1855 by Lord Kelvin to model the transatlantic telegraph cable and was shown to be relevant to neurons by Hodgkin and Rushton in 1946. In simple cable theory, the neuron is treated as an electrically passive, perfectly cylindrical transmission cable, which can be described by a partial differential equation. 

${\displaystyle \tau {\frac {\partial V}{\partial t}}=\lambda ^{2}{\frac {\partial ^{2}V}{\partial x^{2}}}-V}$

where V(x, t) is the voltage across the membrane at a time t and a position x along the length of the neuron, and where λ and τ are the characteristic length and time scales on which those voltages decay in response to a stimulus. Referring to the circuit diagram on the right, these scales can be determined from the resistances and capacitances per unit length.

${\displaystyle \tau =\ r_{m}c_{m}\,}$

${\displaystyle \lambda ={\sqrt {\frac {r_{m}}{r_{\ell }}}}}$

These time and length-scales can be used to understand the dependence of the conduction velocity on the diameter of the neuron in un-myelinated fibers. For example, the time-scale τ increases with both the membrane resistance r_m and capacitance c_m. As the capacitance increases, more charge must be transferred to produce a given trans-membrane voltage (by the equation Q = CV); as the resistance increases, less charge is transferred per unit time, making the equilibration slower. In a similar manner, if the internal resistance per unit length r_i is lower in one axon than in another (e.g., because the radius of the former is larger), the spatial decay length λ becomes longer and the conduction velocity of an action potential should increase. If the trans-membrane resistance r_m is increased, that lowers the average "leakage" current across the membrane, likewise causing λ to become longer, increasing the conduction velocity.

Termination

Chemical synapses

In general, action potentials that reach the synaptic knobs cause a neurotransmitter to be released into the synaptic cleft. Neurotransmitters are small molecules that may open ion channels in the postsynaptic cell; most axons have the same neurotransmitter at all of their termini. The arrival of the action potential opens voltage-sensitive calcium channels in the presynaptic membrane; the influx of calcium causes vesicles filled with neurotransmitter to migrate to the cell's surface and release their contents into the synaptic cleft. This complex process is inhibited by the neurotoxins tetanospasmin and botulinum toxin, which are responsible for tetanus and botulism, respectively.

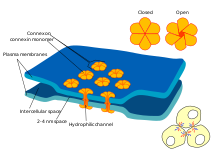
Electrical synapses between excitable cells allow ions to pass directly from one cell to another, and are much faster than chemical synapses.

Electrical synapses

Some synapses dispense with the "middleman" of the neurotransmitter, and connect the presynaptic and postsynaptic cells together. When an action potential reaches such a synapse, the ionic currents flowing into the presynaptic cell can cross the barrier of the two cell membranes and enter the postsynaptic cell through pores known as connexons. Thus, the ionic currents of the presynaptic action potential can directly stimulate the postsynaptic cell. Electrical synapses allow for faster transmission because they do not require the slow diffusion of neurotransmitters across the synaptic cleft. Hence, electrical synapses are used whenever fast response and coordination of timing are crucial, as in escape reflexes, the retina of vertebrates, and the heart.

Neuromuscular junctions

A special case of a chemical synapse is the neuromuscular junction, in which the axon of a motor neuron terminates on a muscle fiber. In such cases, the released neurotransmitter is acetylcholine, which binds to the acetylcholine receptor, an integral membrane protein in the membrane (the sarcolemma) of the muscle fiber. However, the acetylcholine does not remain bound; rather, it dissociates and is hydrolyzed by the enzyme, acetylcholinesterase, located in the synapse. This enzyme quickly reduces the stimulus to the muscle, which allows the degree and timing of muscular contraction to be regulated delicately. Some poisons inactivate acetylcholinesterase to prevent this control, such as the nerve agents sarin and tabun, and the insecticides diazinon and malathion.

Other cell types

Cardiac action potentials

Phases of a cardiac action potential. The sharp rise in voltage ("0") corresponds to the influx of sodium ions, whereas the two decays ("1" and "3", respectively) correspond to the sodium-channel inactivation and the repolarizing eflux of potassium ions. The characteristic plateau ("2") results from the opening of voltage-sensitive calcium channels.

 

The cardiac action potential differs from the neuronal action potential by having an extended plateau, in which the membrane is held at a high voltage for a few hundred milliseconds prior to being repolarized by the potassium current as usual. This plateau is due to the action of slower calcium channels opening and holding the membrane voltage near their equilibrium potential even after the sodium channels have inactivated.

The cardiac action potential plays an important role in coordinating the contraction of the heart. The cardiac cells of the sinoatrial node provide the pacemaker potential that synchronizes the heart. The action potentials of those cells propagate to and through the atrioventricular node (AV node), which is normally the only conduction pathway between the atria and the ventricles. Action potentials from the AV node travel through the bundle of His and thence to the Purkinje fibers. Conversely, anomalies in the cardiac action potential—whether due to a congenital mutation or injury—can lead to human pathologies, especially arrhythmias. Several anti-arrhythmia drugs act on the cardiac action potential, such as quinidine, lidocaine, beta blockers, and verapamil.

Muscular action potentials

The action potential in a normal skeletal muscle cell is similar to the action potential in neurons. Action potentials result from the depolarization of the cell membrane (the sarcolemma), which opens voltage-sensitive sodium channels; these become inactivated and the membrane is repolarized through the outward current of potassium ions. The resting potential prior to the action potential is typically −90mV, somewhat more negative than typical neurons. The muscle action potential lasts roughly 2–4 ms, the absolute refractory period is roughly 1–3 ms, and the conduction velocity along the muscle is roughly 5 m/s. The action potential releases calcium ions that free up the tropomyosin and allow the muscle to contract. Muscle action potentials are provoked by the arrival of a pre-synaptic neuronal action potential at the neuromuscular junction, which is a common target for neurotoxins.

Plant action potentials

Plant and fungal cells  are also electrically excitable. The fundamental difference from animal action potentials is that the depolarization in plant cells is not accomplished by an uptake of positive sodium ions, but by release of negative chloride ions. Together with the following release of positive potassium ions, which is common to plant and animal action potentials, the action potential in plants infers, therefore, an osmotic loss of salt (KCl), whereas the animal action potential is osmotically neutral, when equal amounts of entering sodium and leaving potassium cancel each other osmotically. The interaction of electrical and osmotic relations in plant cells  indicates an osmotic function of electrical excitability in the common, unicellular ancestors of plants and animals under changing salinity conditions, whereas the present function of rapid signal transmission is seen as a younger accomplishment of metazoan cells in a more stable osmotic environment. It must be assumed that the familiar signalling function of action potentials in some vascular plants (e.g. Mimosa pudica) arose independently from that in metazoan excitable cells.

Taxonomic distribution and evolutionary advantages

Action potentials are found throughout multicellular organisms, including plants, invertebrates such as insects, and vertebrates such as reptiles and mammals. Sponges seem to be the main phylum of multicellular eukaryotes that does not transmit action potentials, although some studies have suggested that these organisms have a form of electrical signaling, too. The resting potential, as well as the size and duration of the action potential, have not varied much with evolution, although the conduction velocity does vary dramatically with axonal diameter and myelination. 

Comparison of action potentials (APs) from a representative cross-section of animals

Animal	Cell type	Resting potential (mV)	AP increase (mV)	AP duration (ms)	Conduction speed (m/s)
Squid (Loligo)	Giant axon	−60	120	0.75	35
Earthworm (Lumbricus)	Median giant fiber	−70	100	1.0	30
Cockroach (Periplaneta)	Giant fiber	−70	80–104	0.4	10
Frog (Rana)	Sciatic nerve axon	−60 to −80	110–130	1.0	7–30
Cat (Felis)	Spinal motor neuron	−55 to −80	80–110	1–1.5	30–120

Given its conservation throughout evolution, the action potential seems to confer evolutionary advantages. One function of action potentials is rapid, long-range signaling within the organism; the conduction velocity can exceed 110 m/s, which is one-third the speed of sound. For comparison, a hormone molecule carried in the bloodstream moves at roughly 8 m/s in large arteries. Part of this function is the tight coordination of mechanical events, such as the contraction of the heart. A second function is the computation associated with its generation. Being an all-or-none signal that does not decay with transmission distance, the action potential has similar advantages to digital electronics. The integration of various dendritic signals at the axon hillock and its thresholding to form a complex train of action potentials is another form of computation, one that has been exploited biologically to form central pattern generators and mimicked in artificial neural networks.

Experimental methods

Giant axons of the longfin inshore squid (Doryteuthis pealeii) were crucial for scientists to understand the action potential.

 

The study of action potentials has required the development of new experimental methods. The initial work, prior to 1955, was carried out primarily by Alan Lloyd Hodgkin and Andrew Fielding Huxley, who were, along John Carew Eccles, awarded the 1963 Nobel Prize in Physiology or Medicine for their contribution to the description of the ionic basis of nerve conduction. It focused on three goals: isolating signals from single neurons or axons, developing fast, sensitive electronics, and shrinking electrodes enough that the voltage inside a single cell could be recorded.

The first problem was solved by studying the giant axons found in the neurons of the squid (Loligo forbesii and Doryteuthis pealeii, at the time classified as Loligo pealeii). These axons are so large in diameter (roughly 1 mm, or 100-fold larger than a typical neuron) that they can be seen with the naked eye, making them easy to extract and manipulate. However, they are not representative of all excitable cells, and numerous other systems with action potentials have been studied.

The second problem was addressed with the crucial development of the voltage clamp, which permitted experimenters to study the ionic currents underlying an action potential in isolation, and eliminated a key source of electronic noise, the current I_C associated with the capacitance C of the membrane.^[60] Since the current equals C times the rate of change of the transmembrane voltage V_m, the solution was to design a circuit that kept V_m fixed (zero rate of change) regardless of the currents flowing across the membrane. Thus, the current required to keep V_m at a fixed value is a direct reflection of the current flowing through the membrane. Other electronic advances included the use of Faraday cages and electronics with high input impedance, so that the measurement itself did not affect the voltage being measured.

The third problem, that of obtaining electrodes small enough to record voltages within a single axon without perturbing it, was solved in 1949 with the invention of the glass micropipette electrode, which was quickly adopted by other researchers. Refinements of this method are able to produce electrode tips that are as fine as 100 Å (10 nm), which also confers high input impedance. Action potentials may also be recorded with small metal electrodes placed just next to a neuron, with neurochips containing EOSFETs, or optically with dyes that are sensitive to Ca²⁺ or to voltage.

As revealed by a patch clamp electrode, an ion channel has two states: open (high conductance) and closed (low conductance).

 

While glass micropipette electrodes measure the sum of the currents passing through many ion channels, studying the electrical properties of a single ion channel became possible in the 1970s with the development of the patch clamp by Erwin Neher and Bert Sakmann. For this discovery, they were awarded the Nobel Prize in Physiology or Medicine in 1991. Patch-clamping verified that ionic channels have discrete states of conductance, such as open, closed and inactivated.

Optical imaging technologies have been developed in recent years to measure action potentials, either via simultaneous multisite recordings or with ultra-spatial resolution. Using voltage-sensitive dyes, action potentials have been optically recorded from a tiny patch of cardiomyocyte membrane.

Neurotoxins

Tetrodotoxin is a lethal toxin found in pufferfish that inhibits the voltage-sensitive sodium channel, halting action potentials.

 

Several neurotoxins, both natural and synthetic, are designed to block the action potential. Tetrodotoxin from the pufferfish and saxitoxin from the Gonyaulax (the dinoflagellate genus responsible for "red tides") block action potentials by inhibiting the voltage-sensitive sodium channel; similarly, dendrotoxin from the black mamba snake inhibits the voltage-sensitive potassium channel. Such inhibitors of ion channels serve an important research purpose, by allowing scientists to "turn off" specific channels at will, thus isolating the other channels' contributions; they can also be useful in purifying ion channels by affinity chromatography or in assaying their concentration. However, such inhibitors also make effective neurotoxins, and have been considered for use as chemical weapons. Neurotoxins aimed at the ion channels of insects have been effective insecticides; one example is the synthetic permethrin, which prolongs the activation of the sodium channels involved in action potentials. The ion channels of insects are sufficiently different from their human counterparts that there are few side effects in humans.

History

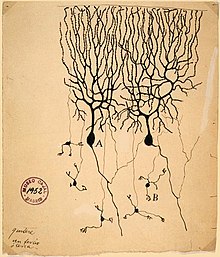
Image of two Purkinje cells (labeled as A) drawn by Santiago Ramón y Cajal in 1899. Large trees of dendrites feed into the soma, from which a single axon emerges and moves generally downwards with a few branch points. The smaller cells labeled B are granule cells.

 

The role of electricity in the nervous systems of animals was first observed in dissected frogs by Luigi Galvani, who studied it from 1791 to 1797. Galvani's results stimulated Alessandro Volta to develop the Voltaic pile—the earliest-known electric battery—with which he studied animal electricity (such as electric eels) and the physiological responses to applied direct-current voltages.

Scientists of the 19th century studied the propagation of electrical signals in whole nerves (i.e., bundles of neurons) and demonstrated that nervous tissue was made up of cells, instead of an interconnected network of tubes (a reticulum). Carlo Matteucci followed up Galvani's studies and demonstrated that cell membranes had a voltage across them and could produce direct current. Matteucci's work inspired the German physiologist, Emil du Bois-Reymond, who discovered the action potential in 1843. The conduction velocity of action potentials was first measured in 1850 by du Bois-Reymond's friend, Hermann von Helmholtz. To establish that nervous tissue is made up of discrete cells, the Spanish physician Santiago Ramón y Cajal and his students used a stain developed by Camillo Golgi to reveal the myriad shapes of neurons, which they rendered painstakingly. For their discoveries, Golgi and Ramón y Cajal were awarded the 1906 Nobel Prize in Physiology. Their work resolved a long-standing controversy in the neuroanatomy of the 19th century; Golgi himself had argued for the network model of the nervous system. 

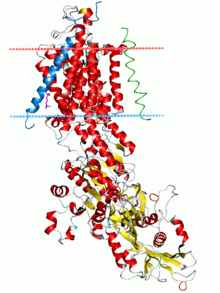
Ribbon diagram of the sodium–potassium pump in its E2-Pi state. The estimated boundaries of the lipid bilayer are shown as blue (intracellular) and red (extracellular) planes.

 

The 20th century was a significant era for electrophysiology. In 1902 and again in 1912, Julius Bernstein advanced the hypothesis that the action potential resulted from a change in the permeability of the axonal membrane to ions. Bernstein's hypothesis was confirmed by Ken Cole and Howard Curtis, who showed that membrane conductance increases during an action potential. In 1907, Louis Lapicque suggested that the action potential was generated as a threshold was crossed, what would be later shown as a product of the dynamical systems of ionic conductances. In 1949, Alan Hodgkin and Bernard Katz refined Bernstein's hypothesis by considering that the axonal membrane might have different permeabilities to different ions; in particular, they demonstrated the crucial role of the sodium permeability for the action potential. They made the first actual recording of the electrical changes across the neuronal membrane that mediate the action potential. This line of research culminated in the five 1952 papers of Hodgkin, Katz and Andrew Huxley, in which they applied the voltage clamp technique to determine the dependence of the axonal membrane's permeabilities to sodium and potassium ions on voltage and time, from which they were able to reconstruct the action potential quantitatively. Hodgkin and Huxley correlated the properties of their mathematical model with discrete ion channels that could exist in several different states, including "open", "closed", and "inactivated". Their hypotheses were confirmed in the mid-1970s and 1980s by Erwin Neher and Bert Sakmann, who developed the technique of patch clamping to examine the conductance states of individual ion channels. In the 21st century, researchers are beginning to understand the structural basis for these conductance states and for the selectivity of channels for their species of ion, through the atomic-resolution crystal structures, fluorescence distance measurements and cryo-electron microscopy studies.

Julius Bernstein was also the first to introduce the Nernst equation for resting potential across the membrane; this was generalized by David E. Goldman to the eponymous Goldman equation in 1943. The sodium–potassium pump was identified in 1957 and its properties gradually elucidated, culminating in the determination of its atomic-resolution structure by X-ray crystallography. The crystal structures of related ionic pumps have also been solved, giving a broader view of how these molecular machines work.

Quantitative models

Equivalent electrical circuit for the Hodgkin–Huxley model of the action potential. I_m and V_m represent the current through, and the voltage across, a small patch of membrane, respectively. The C_m represents the capacitance of the membrane patch, whereas the four g's represent the conductances of four types of ions. The two conductances on the left, for potassium (K) and sodium (Na), are shown with arrows to indicate that they can vary with the applied voltage, corresponding to the voltage-sensitive ion channels. The two conductances on the right help determine the resting membrane potential.

 

Mathematical and computational models are essential for understanding the action potential, and offer predictions that may be tested against experimental data, providing a stringent test of a theory. The most important and accurate of the early neural models is the Hodgkin–Huxley model, which describes the action potential by a coupled set of four ordinary differential equations (ODEs). Although the Hodgkin–Huxley model may be a simplification with few limitations compared to the realistic nervous membrane as it exists in nature, its complexity has inspired several even-more-simplified models, such as the Morris–Lecar model and the FitzHugh–Nagumo model, both of which have only two coupled ODEs. The properties of the Hodgkin–Huxley and FitzHugh–Nagumo models and their relatives, such as the Bonhoeffer–van der Pol model, have been well-studied within mathematics, computation and electronics. However the simple models of generator potential and action potential fail to accurately reproduce the near threshold neural spike rate and spike shape, specifically for the mechanoreceptors like the Pacinian corpuscle. More modern research has focused on larger and more integrated systems; by joining action-potential models with models of other parts of the nervous system (such as dendrites and synapses), researchers can study neural computation and simple reflexes, such as escape reflexes and others controlled by central pattern generators.