Observational (random vs. systematic) error

From Wikipedia, the free encyclopedia

Observational error (or measurement error) is the difference between a measured value of a quantity and its true value. In statistics, an error is not a "mistake". Variability is an inherent part of the results of measurements and of the measurement process.

Measurement errors can be divided into two components: random error and systematic error.

Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by an inaccuracy (involving either the observation or measurement process) inherent to the system. Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.

Science and experiments

When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are "errors" in the sense in which that term is used in statistics; see errors and residuals in statistics. 

Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:

1. Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case
2. Random error which may vary from observation to another.

Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error. 

Random error (or random variation) is due to factors which cannot or will not be controlled. Some possible reason to forgo controlling for these random errors is because it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time, or is fundamentally probabilistic (as is the case in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.

Random errors versus systematic errors

Measurement errors can be divided into two components: random error and systematic error.

Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter's interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements, and reduced by averaging multiple measurements. 

Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms. Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter's interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.

Sources of systematic error

Imperfect calibration

Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period. 

Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.

Quantity

Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero, and underestimated when it will be below zero.

Drift

Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement. 

If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. A systematic error is present if the stopwatch is checked against the 'speaking clock' of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running. 

Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards. 

Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.

Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.

Sources of random error

The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.

Surveys

The term "Observational error" is also sometimes used to refer to response errors and some other types of non-sampling error. In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent's inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1995) and Bland and Altman (1996).

These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error. Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments or predicting this quality using the Survey Quality Predictor software (SQP). This information about the quality can also be used in order to correct for measurement error.

Effect on regression analysis

If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R² will be lower than it would be with perfect measurement. 

However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.

Accuracy and precision

From Wikipedia, the free encyclopedia

Precision is a description of random errors, a measure of statistical variability.

Accuracy has two definitions:

1. More commonly, it is a description of systematic errors, a measure of statistical bias; low accuracy causes a difference between a result and a "true" value. ISO calls this trueness.
2. Alternatively, ISO defines accuracy as describing a combination of both types of observational error above (random and systematic), so high accuracy requires both high precision and high trueness.

In simplest terms, given a set of data points from repeated measurements of the same quantity, the set can be said to be precise if the values are close to each other, while the set can be said to be accurate if their average is close to the true value of the quantity being measured. In the first, more common definition above, the two concepts are independent of each other, so a particular set of data can be said to be either accurate, or precise, or both, or neither.

Common technical definition

Accuracy is the proximity of measurement results to the true value; precision is the degree to which repeated (or reproducible) measurements under unchanged conditions show the same results.

 

In the fields of science and engineering, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's true value. The precision of a measurement system, related to reproducibility and repeatability, is the degree to which repeated measurements under unchanged conditions show the same results. Although the two words precision and accuracy can be synonymous in colloquial use, they are deliberately contrasted in the context of the scientific method. 

The field of statistics, where the interpretation of measurements plays a central role, prefers to use the terms bias and variability instead of accuracy and precision: bias is the amount of inaccuracy and variability is the amount of imprecision.

A measurement system can be accurate but not precise, precise but not accurate, neither, or both. For example, if an experiment contains a systematic error, then increasing the sample size generally increases precision but does not improve accuracy. The result would be a consistent yet inaccurate string of results from the flawed experiment. Eliminating the systematic error improves accuracy but does not change precision. 

A measurement system is considered valid if it is both accurate and precise. Related terms include bias (non-random or directed effects caused by a factor or factors unrelated to the independent variable) and error (random variability). 

The terminology is also applied to indirect measurements—that is, values obtained by a computational procedure from observed data. 

In addition to accuracy and precision, measurements may also have a measurement resolution, which is the smallest change in the underlying physical quantity that produces a response in the measurement. 

In numerical analysis, accuracy is also the nearness of a calculation to the true value; while precision is the resolution of the representation, typically defined by the number of decimal or binary digits.

In military terms, accuracy refers primarily to the accuracy of fire (or "justesse de tir"), the precision of fire expressed by the closeness of a grouping of shots at and around the centre of the target.

Quantification

In industrial instrumentation, accuracy is the measurement tolerance, or transmission of the instrument and defines the limits of the errors made when the instrument is used in normal operating conditions.

Ideally a measurement device is both accurate and precise, with measurements all close to and tightly clustered around the true value. The accuracy and precision of a measurement process is usually established by repeatedly measuring some traceable reference standard. Such standards are defined in the International System of Units (abbreviated SI from French: Système international d'unités) and maintained by national standards organizations such as the National Institute of Standards and Technology in the United States. 

This also applies when measurements are repeated and averaged. In that case, the term standard error is properly applied: the precision of the average is equal to the known standard deviation of the process divided by the square root of the number of measurements averaged. Further, the central limit theorem shows that the probability distribution of the averaged measurements will be closer to a normal distribution than that of individual measurements. 

With regard to accuracy we can distinguish:

• the difference between the mean of the measurements and the reference value, the bias. Establishing and correcting for bias is necessary for calibration.
• the combined effect of that and precision.

A common convention in science and engineering is to express accuracy and/or precision implicitly by means of significant figures. Here, when not explicitly stated, the margin of error is understood to be one-half the value of the last significant place. For instance, a recording of 843.6 m, or 843.0 m, or 800.0 m would imply a margin of 0.05 m (the last significant place is the tenths place), while a recording of 8436 m would imply a margin of error of 0.5 m (the last significant digits are the units). 

A reading of 8,000 m, with trailing zeroes and no decimal point, is ambiguous; the trailing zeroes may or may not be intended as significant figures. To avoid this ambiguity, the number could be represented in scientific notation: 8.0 × 10³ m indicates that the first zero is significant (hence a margin of 50 m) while 8.000 × 10³ m indicates that all three zeroes are significant, giving a margin of 0.5 m. Similarly, it is possible to use a multiple of the basic measurement unit: 8.0 km is equivalent to 8.0 × 10³ m. In fact, it indicates a margin of 0.05 km (50 m). However, reliance on this convention can lead to false precision errors when accepting data from sources that do not obey it. For example, a source reporting a number like 153,753 with precision +/- 5,000 looks like it has precision +/- 0.5. Under the convention it would have been rounded to 154,000. 

Precision includes:

• repeatability — the variation arising when all efforts are made to keep conditions constant by using the same instrument and operator, and repeating during a short time period; and
• reproducibility — the variation arising using the same measurement process among different instruments and operators, and over longer time periods.

ISO definition (ISO 5725)

According to ISO 5725-1, Accuracy consists of trueness (proximity of measurement results to the true value) and precision (repeatability or reproducibility of the measurement)

 

A shift in the meaning of these terms appeared with the publication of the ISO 5725 series of standards in 1994, which is also reflected in the 2008 issue of the "BIPM International Vocabulary of Metrology" (VIM), items 2.13 and 2.14.

According to ISO 5725-1, the general term "accuracy" is used to describe the closeness of a measurement to the true value. When the term is applied to sets of measurements of the same measurand, it involves a component of random error and a component of systematic error. In this case trueness is the closeness of the mean of a set of measurement results to the actual (true) value and precision is the closeness of agreement among a set of results. 

ISO 5725-1 and VIM also avoid the use of the term "bias", previously specified in BS 5497-1, because it has different connotations outside the fields of science and engineering, as in medicine and law. 

Accuracy of a target grouping according to BIPM and ISO 5725

• 

  Low accuracy due to poor precision
  
• 

  Low accuracy due to poor trueness
  

In binary classification

Accuracy is also used as a statistical measure of how well a binary classification test correctly identifies or excludes a condition. That is, the accuracy is the proportion of true results (both true positives and true negatives) among the total number of cases examined. To make the context clear by the semantics, it is often referred to as the "Rand accuracy" or "Rand index". It is a parameter of the test. The formula for quantifying binary accuracy is:

Accuracy = (TP+TN)/(TP+TN+FP+FN)

where: TP = True positive; FP = False positive; TN = True negative; FN = False negative

In psychometrics and psychophysics

In psychometrics and psychophysics, the term accuracy is interchangeably used with validity and constant error. Precision is a synonym for reliability and variable error. The validity of a measurement instrument or psychological test is established through experiment or correlation with behavior. Reliability is established with a variety of statistical techniques, classically through an internal consistency test like Cronbach's alpha to ensure sets of related questions have related responses, and then comparison of those related question between reference and target population.^{[citation needed]}

In logic simulation

In logic simulation, a common mistake in evaluation of accurate models is to compare a logic simulation model to a transistor circuit simulation model. This is a comparison of differences in precision, not accuracy. Precision is measured with respect to detail and accuracy is measured with respect to reality.

In information systems

Information retrieval systems, such as databases and web search engines, are evaluated by many different metrics, some of which are derived from the confusion matrix, which divides results into true positives (documents correctly retrieved), true negatives (documents correctly not retrieved), false positives (documents incorrectly retrieved), and false negatives (documents incorrectly not retrieved). Commonly used metrics include the notions of precision and recall. In this context, precision is defined as the fraction of retrieved documents which are relevant to the query (true positives divided by true+false positives), using a set of ground truth relevant results selected by humans. Recall is defined as the fraction of relevant documents retrieved compared to the total number of relevant documents (true positives divided by true positives+false negatives). Less commonly, the metric of accuracy is used, is defined as the total number of correct classifications (true positives plus true negatives) divided by the total number of documents. 

None of these metrics take into account the ranking of results. Ranking is very important for web search engines because readers seldom go past the first page of results, and there are too many documents on the web to manually classify all of them as to whether they should be included or excluded from a given search. Adding a cutoff at a particular number of results takes ranking into account to some degree. The measure precision at k, for example, is a measure of precision looking only at the top ten (k=10) search results. More sophisticated metrics, such as discounted cumulative gain, take into account each individual ranking, and are more commonly used where this is important.

Metrology

From Wikipedia, the free encyclopedia

A scientist stands in front of the Microarcsecond Metrology (MAM) testbed.

Metrology is the science of measurement. It establishes a common understanding of units, crucial in linking human activities. Modern metrology has its roots in the French Revolution's political motivation to standardise units in France, when a length standard taken from a natural source was proposed. This led to the creation of the decimal-based metric system in 1795, establishing a set of standards for other types of measurements. Several other countries adopted the metric system between 1795 and 1875; to ensure conformity between the countries, the Bureau International des Poids et Mesures (BIPM) was established by the Metre Convention. This has evolved into the International System of Units (SI) as a result of a resolution at the 11th Conference Generale des Poids et Mesures (CGPM) in 1960.

Metrology is divided into three basic overlapping activities. The first being the definition of units of measurement, second the realisation of these units of measurement in practice, and last traceability, which is linking measurements made in practice to the reference standards. These overlapping activities are used in varying degrees by the three basic sub-fields of Metrology. The sub-fields are scientific or fundamental metrology, which is concerned with the establishment of units of measurement, Applied, technical or industrial metrology, the application of measurement to manufacturing and other processes in society, and Legal metrology, which covers the regulation and statutory requirements for measuring instruments and the methods of measurement. 

In each country, a national measurement system (NMS) exists as a network of laboratories, calibration facilities and accreditation bodies which implement and maintain its metrology infrastructure. The NMS affects how measurements are made in a country and their recognition by the international community, which has a wide-ranging impact in its society (including economics, energy, environment, health, manufacturing, industry and consumer confidence). The effects of metrology on trade and economy are some of the easiest-observed societal impacts. To facilitate fair trade, there must be an agreed-upon system of measurement.

History

The ability to measure alone is insufficient; standardisation is crucial for measurements to be meaningful. The first record of a permanent standard was in 2900 BC, when the royal Egyptian cubit was carved from black granite. The cubit was decreed to be the length of the Pharaoh's forearm plus the width of his hand, and replica standards were given to builders. The success of a standardised length for the building of the pyramids is indicated by the lengths of their bases differing by no more than 0.05 percent.

Other civilizations produced generally accepted measurement standards, with Roman and Greek architecture based on distinct systems of measurement. The collapse of the empires and the Dark Ages which followed them lost much measurement knowledge and standardisation. Although local systems of measurement were common, comparability was difficult since many local systems were incompatible. England established the Assize of Measures to create standards for length measurements in 1196, and the 1215 Magna Carta included a section for the measurement of wine and beer.

Modern metrology has its roots in the French Revolution. With a political motivation to harmonise units throughout France, a length standard based on a natural source was proposed. In March 1791, the metre was defined. This led to the creation of the decimal-based metric system in 1795, establishing standards for other types of measurements. Several other countries adopted the metric system between 1795 and 1875; to ensure international conformity, the International Bureau of Weights and Measures (French: Bureau International des Poids et Mesures, or BIPM) was established by the Metre Convention. Although the BIPM's original mission was to create international standards for units of measurement and relate them to national standards to ensure conformity, its scope has broadened to include electrical and photometric units and ionizing radiation measurement standards. The metric system was modernised in 1960 with the creation of the International System of Units (SI) as a result of a resolution at the 11th General Conference on Weights and Measures (French: Conference Generale des Poids et Mesures, or CGPM).

Subfields

Metrology is defined by the International Bureau of Weights and Measures (BIPM) as "the science of measurement, embracing both experimental and theoretical determinations at any level of uncertainty in any field of science and technology". It establishes a common understanding of units, crucial to human activity. Metrology is a wide reaching field, but can be summarized through three basic activities: the definition of internationally accepted units of measurement, the realisation of these units of measurement in practice, and the application of chains of traceability (linking measurements to reference standards). These concepts apply in different degrees to metrology's three main fields: scientific metrology; applied, technical or industrial metrology, and legal metrology.

Scientific metrology

Scientific metrology is concerned with the establishment of units of measurement, the development of new measurement methods, the realisation of measurement standards, and the transfer of traceability from these standards to users in a society. This type of metrology is considered the top level of metrology which strives for the highest degree of accuracy. BIPM maintains a database of the metrological calibration and measurement capabilities of institutes around the world. These institutes, whose activities are peer-reviewed, provide the fundamental reference points for metrological traceability. In the area of measurement, BIPM has identified nine metrology areas, which are acoustics, electricity and magnetism, length, mass and related quantities, photometry and radiometry, ionizing radiation, time and frequency, thermometry, and chemistry.

There is a proposed redefinition of the SI base units that was formally voted on in November 2018, and will come into effect in May 2019. The motivation in the change of the base units is to make the entire system derivable from physical constants, which requires the removal of the prototype kilogram as it is the last artefact the unit definitions depend on. Scientific metrology plays an important role in this redefinition of the units as precise measurements of the physical constants is required to have accurate definitions of the base units. To redefine the value of a kilogram without an artefact the value of the Planck constant must be known to twenty parts per billion. Scientific metrology, through the development of the Kibble balance and the Avogadro project, has produced a value of Planck constant with low enough uncertainty to allow for a redefinition of the kilogram.

Applied, technical or industrial metrology

Applied, technical or industrial metrology is concerned with the application of measurement to manufacturing and other processes and their use in society, ensuring the suitability of measurement instruments, their calibration and quality control. Producing good measurements is important in industry as it has an impact on the value and quality of the end product, and a 10–15% impact on production costs. Although the emphasis in this area of metrology is on the measurements themselves, traceability of the measuring-device calibration is necessary to ensure confidence in the measurement. Recognition of the metrological competence in industry can be achieved through mutual recognition agreements, accreditation, or peer review. Industrial metrology is important to a country's economic and industrial development, and the condition of a country's industrial-metrology program can indicate its economic status.

Legal metrology

Legal metrology "concerns activities which result from statutory requirements and concern measurement, units of measurement, measuring instruments and methods of measurement and which are performed by competent bodies". Such statutory requirements may arise from the need for protection of health, public safety, the environment, enabling taxation, protection of consumers and fair trade. The International Organization for Legal Metrology (OIML) was established to assist in harmonising regulations across national boundaries to ensure that legal requirements do not inhibit trade. This harmonisation ensures that certification of measuring devices in one country is compatible with another countries certification process, allowing the trade of the measuring devices and the products that rely on them. WELMEC was established in 1990 to promote cooperation in the field of legal metrology in the European Union and among European Free Trade Association (EFTA) member states. In the United States legal metrology is under the authority of the Office of Weights and Measures of National Institute of Standards and Technology (NIST), enforced by the individual states.

Concepts

Definition of units

The International System of Units (SI) defines seven base units: length, mass, time, electric current, thermodynamic temperature, amount of substance, and luminous intensity. By convention, each of these units are considered to be mutually independent of each other; however, in reality they are interdependent given some definitions contain other base SI Units. All other SI units are derived from the seven base units.

SI base units and standards

Base quantity	Name	Symbol	Definition
Length	metre	m	The length of the path travelled by light in a vacuum during a time interval of 1/299792458 of a second
Mass	kilogram	kg	The mass of the international prototype kilogram (IPK)
Time	second	s	The duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom
Electric current	ampere	A	A constant current which, if maintained in two straight parallel conductors of infinite length and negligible circular cross-section, placed 1 metre apart in a vacuum, would produce a force equal to 2×10−7 newtons per metre
Thermodynamic temperature	kelvin	K	The fraction 1/273.16 of the thermodynamic temperature of the triple point of water
Amount of substance	mole	mol	The amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon-12
Luminous intensity	candela	cd	The luminous intensity, in a given direction, of a source emitting monochromatic radiation of a frequency of 540×1012 Hz with a radiant intensity in that direction of 1/683 watt per steradian

Since the base units are the reference points for all measurements taken in SI units, if the reference value changed all prior measurements would be incorrect. If a piece of the international prototype kilogram snapped off, it would still be defined as a kilogram; all previous measured values of a kilogram would be heavier. The importance of reproducible SI units has led the BIPM to begin defining base SI units in terms of physical constants. By defining base SI units with respect to physical constants, they are realisable with a higher level of precision and reproducibility. With the redefinition of the SI units occurring on May 20th, 2019 the kilogram, ampere, kelvin, and mole will then be defined by setting exact numerical values for the Planck constant (h), the elementary electric charge (e), the Boltzmann constant (k), and the Avogadro constant (N_A), respectively. The metre and candela are already defined by physical constants, subject to correction to their present definitions. The new definitions aim to improve the SI without changing the size of any units, thus ensuring continuity with existing measurements.

Realisation of units

Computer-generated image realising the international prototype kilogram (IPK), made from an alloy of 90-percent platinum and 10-percent iridium by weight

The realisation of a unit of measure is its conversion into reality. Three possible methods of realisation are defined by the international vocabulary of metrology (VIM): a physical realisation of the unit from its definition, a highly-reproducible measurement as a reproduction of the definition (such as the quantum Hall effect for the ohm), and the use of a material object as the measurement standard.

Standards

A standard (or etalon) is an object, system, or experiment with a defined relationship to a unit of measurement of a physical quantity. Standards are the fundamental reference for a system of weights and measures by realising, preserving, or reproducing a unit against which measuring devices can be compared. There are three levels of standards in the hierarchy of metrology: primary, secondary, and working standards. Primary standards (the highest quality) do not reference any other standards. Secondary standards are calibrated with reference to a primary standard. Working standards, used to calibrate (or check) measuring instruments or other material measures, are calibrated with respect to secondary standards. The hierarchy preserves the quality of the higher standards. An example of a standard would be gauge blocks for length. A gauge block is a block of metal or ceramic with two opposing faces ground precisely flat and parallel, a precise distance apart. The length of the path of light in vacuum during a time interval of 1/299,792,458 of a second is embodied in an artefact standard such as a gauge block; this gauge block is then a primary standard which can be used to calibrate secondary standards through mechanical comparators.

Traceability and calibration

Metrology traceability pyramid

Metrological traceability is defined as the "property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty". It permits the comparison of measurements, whether the result is compared to the previous result in the same laboratory, a measurement result a year ago, or to the result of a measurement performed anywhere else in the world. The chain of traceability allows any measurement to be referenced to higher levels of measurements back to the original definition of the unit.

Traceability is most often obtained by calibration, establishing the relationship between an indication on a measuring instrument (or secondary standard) and the value of the standard. A calibration is an operation that establishes a relation between a measurement standard with a known measurement uncertainty and the device that is being evaluated. The process will determine the measurement value and uncertainty of the device that is being calibrated and create a traceability link to the measurement standard. The four primary reasons for calibrations are to provide traceability, to ensure that the instrument (or standard) is consistent with other measurements, to determine accuracy, and to establish reliability. Traceability works as a pyramid, at the top level there is the international standards, at the next level national metrology institutes calibrate the primary standards through realisation of the units creating the traceability link from the primary standard and the unit definition. Through subsequent calibrations between national metrology institutes, calibration laboratories, and industry and testing laboratories the realisation of the unit definition is propagated down through the pyramid. The traceability chain works upwards from the bottom of the pyramid, where measurements done by industry and testing laboratories can be directly related to the unit definition at the top through the traceability chain created by calibration.

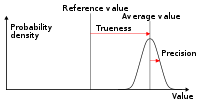
Uncertainty

Measurement uncertainty is a value associated with a measurement which expresses the spread of possible values associated with the measurand—a quantitative expression of the doubt existing in the measurement. There are two components to the uncertainty of a measurement: the width of the uncertainty interval and the confidence level. The uncertainty interval is a range of values that the measurement value is expected to fall within, while the confidence level is how likely the true value is to fall within the uncertainty interval. Uncertainty is generally expressed as follows:

${\displaystyle Y=y\pm U}$

Coverage factor: k = 2

Where y is the measurement value and U is the uncertainty value and k is the coverage factor indicates the confidence interval. The upper and lower limit of the uncertainty interval can be determined by adding and subtracting the uncertainty value from the measurement value. The coverage factor of k = 2 generally indicates a 95% confidence that the measured value will fall inside the uncertainty interval. Other values of k can be used to indicate a greater or lower confidence on the interval, for example k = 1 and k = 3 generally indicate 66% and 99.7% confidence respectively. The uncertainty value is determined through a combination of statistical analysis of the calibration and uncertainty contribution from other errors in measurement process, which can be evaluated from sources such as the instrument history, manufacturer's specifications, or published information.

International infrastructure

Several international organizations maintain and standardise metrology.

Metre Convention

The Metre Convention created three main international organizations to facilitate standardisation of weights and measures. The first, the General Conference on Weights and Measures (CGPM), provided a forum for representatives of member states. The second, the International Committee for Weights and Measures (CIPM), was an advisory committee of metrologists of high standing. The third, the International Bureau of Weights and Measures (BIPM), provided secretarial and laboratory facilities for the CGPM and CIPM.

General Conference on Weights and Measures

The General Conference on Weights and Measures (French: Conférence générale des poids et mesures, or CGPM) is the convention's principal decision-making body, consisting of delegates from member states and non-voting observers from associate states. The conference usually meets every four to six years to receive and discuss a CIPM report and endorse new developments in the SI as advised by the CIPM. The last meeting was held November 13–16, 2018. On the last day of this conference there was vote on the redefinition of four base units, which the International Committee for Weights and Measures (CIPM) had proposed earlier that year. The new definitions came into force on 20 May 2019.

International Committee for Weights and Measures

The International Committee for Weights and Measures (French: Comité international des poids et mesures, or CIPM) is made up of eighteen (originally fourteen) individuals from a member state of high scientific standing, nominated by the CGPM to advise the CGPM on administrative and technical matters. It is responsible for ten consultative committees (CCs), each of which investigates a different aspect of metrology; one CC discusses the measurement of temperature, another the measurement of mass, and so forth. The CIPM meets annually in Sèvres to discuss reports from the CCs, to submit an annual report to the governments of member states concerning the administration and finances of the BIPM and to advise the CGPM on technical matters as needed. Each member of the CIPM is from a different member state, with France (in recognition of its role in establishing the convention) always having one seat.

International Bureau of Weights and Measures

BIPM seal

The International Bureau of Weights and Measures (French: Bureau international des poids et mesures, or BIPM) is an organisation based in Sèvres, France which has custody of the international prototype kilogram, provides metrology services for the CGPM and CIPM, houses the secretariat for the organisations and hosts their meetings. Over the years, international prototype metres and kilograms have been returned to BIPM headquarters for recalibration. The BIPM director is an ex officio member of the CIPM and a member of all consultative committees.

International Organization of Legal Metrology

The International Organization of Legal Metrology (French: Organisation Internationale de Métrologie Légale, or OIML), is an intergovernmental organization created in 1955 to promote the global harmonisation of the legal metrology procedures facilitating international trade. This harmonisation of technical requirements, test procedures and test-report formats ensure confidence in measurements for trade and reduces the costs of discrepancies and measurement duplication. The OIML publishes a number of international reports in four categories:

• Recommendations: Model regulations to establish metrological characteristics and conformity of measuring instruments
• Informative documents: To harmonise legal metrology
• Guidelines for the application of legal metrology
• Basic publications: Definitions of the operating rules of the OIML structure and system

Although the OIML has no legal authority to impose its recommendations and guidelines on its member countries, it provides a standardised legal framework for those countries to assist the development of appropriate, harmonised legislation for certification and calibration. OIML provides a mutual acceptance arrangement (MAA) for measuring instruments that are subject to legal metrological control, which upon approval allows the evaluation and test reports of the instrument to be accepted in all participating countries. Issuing participants in the agreement issue MAA Type Evaulation Reports of MAA Certificates upon demonstration of compliance with ISO/IEC 17065 and a peer evaluation system to determine competency. This ensures that certification of measuring devices in one country is compatible with the certification process in other participating countries, allowing the trade of the measuring devices and the products that rely on them.

International Laboratory Accreditation Cooperation

The International Laboratory Accreditation Cooperation (ILAC) is an international organisation for accreditation agencies involved in the certification of conformity-assessment bodies. It standardises accreditation practices and procedures, recognising competent calibration facilities and assisting countries developing their own accreditation bodies. ILAC originally began as a conference in 1977 to develop international cooperation for accredited testing and calibration results to facilitate trade. In 2000, 36 members signed the ILAC mutual recognition agreement (MRA), allowing members work to be automatically accepted by other signatories, and in 2012 was expanded to include accreditation of inspection bodies. Through this standardisation, work done in laboratories accredited by signatories is automatically recognised internationally through the MRA. Other work done by ILAC includes promotion of laboratory and inspection body accreditation, and supporting the development of accreditation systems in developing economies.

Joint Committee for Guides in Metrology

The Joint Committee for Guides in Metrology (JCGM) is a committee which created and maintains two metrology guides: Guide to the expression of uncertainty in measurement (GUM) and International vocabulary of metrology – basic and general concepts and associated terms (VIM). The JCGM is a collaboration of eight partner organisations:

• International Bureau of Weights and Measures (BIPM)
• International Electrotechnical Commission (IEC)
• International Federation of Clinical Chemistry and Laboratory Medicine (IFCC)
• International Organization for Standardization (ISO)
• International Union of Pure and Applied Chemistry (IUPAC)
• International Union of Pure and Applied Physics (IUPAP)
• International Organization of Legal Metrology (OIML)
• International Laboratory Accreditation Cooperation (ILAC)

The JCGM has two working groups: JCGM-WG1 and JCGM-WG2. JCGM-WG1 is responsible for the GUM, and JCGM-WG2 for the VIM. Each member organization appoints one representative and up to two experts to attend each meeting, and may appoint up to three experts for each working group.

National infrastructure

A national measurement system (NMS) is a network of laboratories, calibration facilities and accreditation bodies which implement and maintain a country's measurement infrastructure. The NMS sets measurement standards, ensuring the accuracy, consistency, comparability, and reliability of measurements made in the country. The measurements of member countries of the CIPM Mutual Recognition Arrangement (CIPM MRA), an agreement of national metrology institutes, are recognized by other member countries. As of March 2018, there are 102 signatories of the CIPM MRA, consisting of 58 member states, 40 associate states, and 4 international organizations.

Metrology institutes

Overview of a national measurement system

A national metrology institute's (NMI) role in a country's measurement system is to conduct scientific metrology, realise base units, and maintain primary national standards. An NMI provides traceability to international standards for a country, anchoring its national calibration hierarchy. For a national measurement system to be recognized internationally by the CIPM Mutual Recognition Arrangement, an NMI must participate in international comparisons of its measurement capabilities. BIPM maintains a comparison database and a list of calibration and measurement capabilities (CMCs) of the countries participating in the CIPM MRA. Not all countries have a centralised metrology institute; some have a lead NMI and several decentralised institutes specialising in specific national standards. Some examples of NMI's are the National Institute of Standards and Technology (NIST) in the United States, the National Research Council (NRC) in Canada, the Korea Research Institute of Standards and Science (KRISS), and the National Physical Laboratory of India (NPL-India).

Calibration laboratories

Calibration laboratories are generally responsible for calibrations of industrial instrumentation. Calibration laboratories are accredited and provide calibration services to industry firms, which provides a traceability link back to the national metrology institute. Since the calibration laboratories are accredited, they give companies a traceability link to national metrology standards. Examples of calibration laboratories would be ICL Calibration Laboratories, Testo Industrial Services GmbH, and Transcat.

Accreditation bodies

An organisation is accredited when an authoritative body determines, by assessing the organisation's personnel and management systems, that it is competent to provide its services. For international recognition, a country's accreditation body must comply with international requirements and is generally the product of international and regional cooperation. A laboratory is evaluated according to international standards such as ISO/IEC 17025 general requirements for the competence of testing and calibration laboratories. To ensure objective and technically-credible accreditation, the bodies are independent of other national measurement system institutions. The National Association of Testing Authorities in Australia, the United Kingdom Accreditation Service, and National Accreditation Board for Testing and Calibration Laboratories in India, are examples of accreditation bodies.

Impacts

Metrology has wide-ranging impacts on a number of sectors, including economics, energy, the environment, health, manufacturing, industry, and consumer confidence. The effects of metrology on trade and the economy are two of its most-apparent societal impacts. To facilitate fair and accurate trade between countries, there must be an agreed-upon system of measurement. Accurate measurement and regulation of water, fuel, food, and electricity are critical for consumer protection and promote the flow of goods and services between trading partners. A common measurement system and quality standards benefit consumer and producer; production at a common standard reduces cost and consumer risk, ensuring that the product meets consumer needs. Transaction costs are reduced through an increased economy of scale. Several studies have indicated that increased standardisation in measurement has a positive impact on GDP. In the United Kingdom, an estimated 28.4 percent of GDP growth from 1921 to 2013 was the result of standardisation; in Canada between 1981 and 2004 an estimated nine percent of GDP growth was standardisation-related, and in Germany the annual economic benefit of standardisation is an estimated 0.72% of GDP.

Legal metrology has reduced accidental deaths and injuries with measuring devices, such as radar guns and breathalyzers, by improving their efficiency and reliability. Measuring the human body is challenging, with poor repeatability and reproducibility, and advances in metrology help develop new techniques to improve health care and reduce costs. Environmental policy is based on research data, and accurate measurements are important for assessing climate change and environmental regulation. Aside from regulation, metrology is essential in supporting innovation, the ability to measure provides a technical infrastructure and tools that can then be used to pursue further innovation. By providing a technical platform which new ideas can be built upon, easily demonstrated, and shared, measurement standards allow new ideas to be explored and expanded upon.