Johannes Kepler
| |
|---|---|

Portrait of Kepler by an unknown artist, 1610
| |
| Born | December 27, 1571 |
| Died | November 15, 1630 (aged 58)
Free Imperial City of Regensburg, Holy Roman Empire
|
| Residence | Württemberg; Styria; Bohemia; Upper Austria |
| Nationality | German |
| Alma mater | Tübinger Stift, University of Tübingen |
| Known for | Kepler's laws of planetary motion Kepler conjecture Rudolphine Tables |
| Scientific career | |
| Fields | Astronomy, astrology, mathematics and natural philosophy |
| Doctoral advisor | Michael Maestlin |
| Influences | Nicolaus Copernicus Tycho Brahe |
| Influenced | Sir Isaac Newton |
| Signature | |
Johannes Kepler was a German astronomer, mathematician, and astrologer. He is a key figure in the 17th-century scientific revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonices Mundi, and Epitome Astronomiae Copernicanae. These works also provided one of the foundations for Newton's theory of universal gravitation.
Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein. Additionally, he did fundamental work in the field of optics, invented an improved version of the refracting (or Keplerian) telescope, and was mentioned in the telescopic discoveries of his contemporary Galileo Galilei. He was a corresponding member of the Accademia dei Lincei in Rome.
Kepler lived in an era when there was no clear distinction between astronomy and astrology, but there was a strong division between astronomy (a branch of mathematics within the liberal arts) and physics (a branch of natural philosophy). Kepler also incorporated religious arguments and reasoning into his work, motivated by the religious conviction and belief that God had created the world according to an intelligible plan that is accessible through the natural light of reason. Kepler described his new astronomy as "celestial physics", as "an excursion into Aristotle's Metaphysics", and as "a supplement to Aristotle's On the Heavens", transforming the ancient tradition of physical cosmology by treating astronomy as part of a universal mathematical physics.
Early years
Kepler's birthplace, in Weil der Stadt
Kepler was born on December 27, the feast day of St John the Evangelist, 1571, in the Free Imperial City of Weil der Stadt (now part of the Stuttgart Region in the German state of Baden-Württemberg,
30 km west of Stuttgart's center). His grandfather, Sebald Kepler, had
been Lord Mayor of the city. By the time Johannes was born, he had two
brothers and one sister and the Kepler family fortune was in decline.
His father, Heinrich Kepler, earned a precarious living as a mercenary, and he left the family when Johannes was five years old. He was believed to have died in the Eighty Years' War in the Netherlands. His mother, Katharina Guldenmann, an innkeeper's daughter, was a healer and herbalist.
Born prematurely, Johannes claimed to have been weak and sickly as a
child. Nevertheless, he often impressed travelers at his grandfather's
inn with his phenomenal mathematical faculty.
He was introduced to astronomy at an early age, and developed a
love for it that would span his entire life. At age six, he observed the
Great Comet of 1577, writing that he "was taken by [his] mother to a high place to look at it." In 1580, at age nine, he observed another astronomical event, a lunar eclipse, recording that he remembered being "called outdoors" to see it and that the moon "appeared quite red". However, childhood smallpox left him with weak vision and crippled hands, limiting his ability in the observational aspects of astronomy.
As a child, Kepler witnessed the Great Comet of 1577, which attracted the attention of astronomers across Europe.
In 1589, after moving through grammar school, Latin school, and seminary at Maulbronn, Kepler attended Tübinger Stift at the University of Tübingen. There, he studied philosophy under Vitus Müller and theology under Jacob Heerbrand (a student of Philipp Melanchthon at Wittenberg), who also taught Michael Maestlin while he was a student, until he became Chancellor at Tübingen in 1590. He proved himself to be a superb mathematician and earned a reputation as a skilful astrologer, casting horoscopes for fellow students. Under the instruction of Michael Maestlin, Tübingen's professor of mathematics from 1583 to 1631, he learned both the Ptolemaic system and the Copernican system of planetary motion. He became a Copernican at that time. In a student disputation, he defended heliocentrism from both a theoretical and theological perspective, maintaining that the Sun was the principal source of motive power in the universe.
Despite his desire to become a minister, near the end of his studies,
Kepler was recommended for a position as teacher of mathematics and
astronomy at the Protestant school in Graz. He accepted the position in
April 1594, at the age of 23.
Graz (1594–1600)
Mysterium Cosmographicum
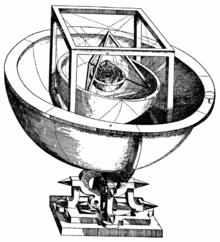
Kepler's Platonic solid model of the Solar System, from Mysterium Cosmographicum (1596)
Kepler's first major astronomical work, Mysterium Cosmographicum (The Cosmographic Mystery, 1596), was the first published defense of the Copernican system. Kepler claimed to have had an epiphany on July 19, 1595, while teaching in Graz, demonstrating the periodic conjunction of Saturn and Jupiter in the zodiac: he realized that regular polygons
bound one inscribed and one circumscribed circle at definite ratios,
which, he reasoned, might be the geometrical basis of the universe.
After failing to find a unique arrangement of polygons that fit known
astronomical observations (even with extra planets added to the system),
Kepler began experimenting with 3-dimensional polyhedra. He found that each of the five Platonic solids could be inscribed and circumscribed by spherical orbs;
nesting these solids, each encased in a sphere, within one another
would produce six layers, corresponding to the six known planets—Mercury, Venus, Earth, Mars, Jupiter, and Saturn. By ordering the solids selectively—octahedron, icosahedron, dodecahedron, tetrahedron, cube—Kepler
found that the spheres could be placed at intervals corresponding to
the relative sizes of each planet's path, assuming the planets circle
the Sun. Kepler also found a formula relating the size of each planet's
orb to the length of its orbital period:
from inner to outer planets, the ratio of increase in orbital period is
twice the difference in orb radius. However, Kepler later rejected this
formula, because it was not precise enough.
As he indicated in the title, Kepler thought he had revealed
God's geometrical plan for the universe. Much of Kepler's enthusiasm for
the Copernican system stemmed from his theological convictions about the connection between the physical and the spiritual; the universe itself was an image of God, with the Sun corresponding to the Father, the stellar sphere to the Son, and the intervening space between to the Holy Spirit. His first manuscript of Mysterium contained an extensive chapter reconciling heliocentrism with biblical passages that seemed to support geocentrism.
Close-up of an inner section of Kepler's model
With the support of his mentor Michael Maestlin, Kepler received
permission from the Tübingen university senate to publish his
manuscript, pending removal of the Bible exegesis and the addition of a simpler, more understandable description of the Copernican system as well as Kepler's new ideas. Mysterium
was published late in 1596, and Kepler received his copies and began
sending them to prominent astronomers and patrons early in 1597; it was
not widely read, but it established Kepler's reputation as a highly
skilled astronomer. The effusive dedication, to powerful patrons as well
as to the men who controlled his position in Graz, also provided a
crucial doorway into the patronage system.
Though the details would be modified in light of his later work,
Kepler never relinquished the Platonist polyhedral-spherist cosmology of
Mysterium Cosmographicum.
His subsequent main astronomical works were in some sense only further
developments of it, concerned with finding more precise inner and outer
dimensions for the spheres by calculating the eccentricities of the
planetary orbits within it. In 1621, Kepler published an expanded second
edition of Mysterium, half as long again as the first, detailing
in footnotes the corrections and improvements he had achieved in the 25
years since its first publication.
In terms of the impact of Mysterium, it can be seen as an important first step in modernizing the theory proposed by Nicolaus Copernicus in his "De revolutionibus orbium coelestium".
Whilst Copernicus sought to advance a heliocentric system in this book,
he resorted to Ptolemaic devices (viz., epicycles and eccentric
circles) in order to explain the change in planets' orbital speed, and
also continued to use as a point of reference the center of the Earth's
orbit rather than that of the Sun "as an aid to calculation and in order
not to confuse the reader by diverging too much from Ptolemy." Modern
astronomy owes much to Mysterium Cosmographicum, despite flaws in
its main thesis, "since it represents the first step in cleansing the
Copernican system of the remnants of the Ptolemaic theory still clinging
to it."
House of Kepler and Barbara Müller in Gössendorf, near Graz (1597–1599)
Marriage to Barbara Müller
In
December 1595, Kepler was introduced to Barbara Müller, a 23-year-old
widow (twice over) with a young daughter, Regina Lorenz, and he began
courting her. Müller, an heiress to the estates of her late husbands,
was also the daughter of a successful mill owner. Her father Jobst
initially opposed a marriage. Even though Kepler had inherited his
grandfather's nobility, Kepler's poverty made him an unacceptable match.
Jobst relented after Kepler completed work on Mysterium, but the
engagement nearly fell apart while Kepler was away tending to the
details of publication. However, Protestant officials—who had helped set
up the match—pressured the Müllers to honor their agreement. Barbara
and Johannes were married on April 27, 1597.
In the first years of their marriage, the Keplers had two
children (Heinrich and Susanna), both of whom died in infancy. In 1602,
they had a daughter (Susanna); in 1604, a son (Friedrich); and in 1607,
another son (Ludwig).
Other research
Following the publication of Mysterium
and with the blessing of the Graz school inspectors, Kepler began an
ambitious program to extend and elaborate his work. He planned four
additional books: one on the stationary aspects of the universe (the Sun
and the fixed stars); one on the planets and their motions; one on the
physical nature of planets and the formation of geographical features
(focused especially on Earth); and one on the effects of the heavens on
the Earth, to include atmospheric optics, meteorology, and astrology.
He also sought the opinions of many of the astronomers to whom he had sent Mysterium, among them Reimarus Ursus (Nicolaus Reimers Bär)—the imperial mathematician to Rudolph II and a bitter rival of Tycho Brahe.
Ursus did not reply directly, but republished Kepler's flattering
letter to pursue his priority dispute over (what is now called) the Tychonic system
with Tycho. Despite this black mark, Tycho also began corresponding
with Kepler, starting with a harsh but legitimate critique of Kepler's
system; among a host of objections, Tycho took issue with the use of
inaccurate numerical data taken from Copernicus. Through their letters,
Tycho and Kepler discussed a broad range of astronomical problems,
dwelling on lunar phenomena and Copernican theory (particularly its
theological viability). But without the significantly more accurate data
of Tycho's observatory, Kepler had no way to address many of these
issues.
Instead, he turned his attention to chronology and "harmony," the numerological relationships among music, mathematics and the physical world, and their astrological
consequences. By assuming the Earth to possess a soul (a property he
would later invoke to explain how the sun causes the motion of planets),
he established a speculative system connecting astrological aspects and astronomical distances to weather
and other earthly phenomena. By 1599, however, he again felt his work
limited by the inaccuracy of available data—just as growing religious
tension was also threatening his continued employment in Graz. In
December of that year, Tycho invited Kepler to visit him in Prague;
on January 1, 1600 (before he even received the invitation), Kepler set
off in the hopes that Tycho's patronage could solve his philosophical
problems as well as his social and financial ones.
Prague (1600–1612)
Work for Tycho Brahe
On February 4, 1600, Kepler met Tycho Brahe and his assistants Franz Tengnagel and Longomontanus at Benátky nad Jizerou
(35 km from Prague), the site where Tycho's new observatory was being
constructed. Over the next two months, he stayed as a guest, analyzing
some of Tycho's observations of Mars; Tycho guarded his data closely,
but was impressed by Kepler's theoretical ideas and soon allowed him
more access. Kepler planned to test his theory from Mysterium Cosmographicum
based on the Mars data, but he estimated that the work would take up to
two years (since he was not allowed to simply copy the data for his own
use). With the help of Johannes Jessenius,
Kepler attempted to negotiate a more formal employment arrangement with
Tycho, but negotiations broke down in an angry argument and Kepler left
for Prague on April 6. Kepler and Tycho soon reconciled and eventually
reached an agreement on salary and living arrangements, and in June,
Kepler returned home to Graz to collect his family.
Political and religious difficulties in Graz dashed his hopes of
returning immediately to Brahe; in hopes of continuing his astronomical
studies, Kepler sought an appointment as a mathematician to Archduke Ferdinand.
To that end, Kepler composed an essay—dedicated to Ferdinand—in which
he proposed a force-based theory of lunar motion: "In Terra inest
virtus, quae Lunam ciet" ("There is a force in the earth which causes
the moon to move").
Though the essay did not earn him a place in Ferdinand's court, it did
detail a new method for measuring lunar eclipses, which he applied
during the July 10 eclipse in Graz. These observations formed the basis
of his explorations of the laws of optics that would culminate in Astronomiae Pars Optica.
On August 2, 1600, after refusing to convert to Catholicism,
Kepler and his family were banished from Graz. Several months later,
Kepler returned, now with the rest of his household, to Prague. Through
most of 1601, he was supported directly by Tycho, who assigned him to
analyzing planetary observations and writing a tract against Tycho's (by
then deceased) rival, Ursus. In September, Tycho secured him a
commission as a collaborator on the new project he had proposed to the
emperor: the Rudolphine Tables that should replace the Prutenic Tables of Erasmus Reinhold.
Two days after Tycho's unexpected death on October 24, 1601, Kepler was
appointed his successor as the imperial mathematician with the
responsibility to complete his unfinished work. The next 11 years as
imperial mathematician would be the most productive of his life.
Advisor to Emperor Rudolph II
Kepler's
primary obligation as imperial mathematician was to provide
astrological advice to the emperor. Though Kepler took a dim view of the
attempts of contemporary astrologers to precisely predict the future or
divine specific events, he had been casting well-received detailed
horoscopes for friends, family, and patrons since his time as a student
in Tübingen. In addition to horoscopes for allies and foreign leaders,
the emperor sought Kepler's advice in times of political trouble.
Rudolph was actively interested in the work of many of his court
scholars (including numerous alchemists) and kept up with Kepler's work in physical astronomy as well.
Officially, the only acceptable religious doctrines in Prague were Catholic and Utraquist,
but Kepler's position in the imperial court allowed him to practice his
Lutheran faith unhindered. The emperor nominally provided an ample
income for his family, but the difficulties of the over-extended
imperial treasury meant that actually getting hold of enough money to
meet financial obligations was a continual struggle. Partly because of
financial troubles, his life at home with Barbara was unpleasant, marred
with bickering and bouts of sickness. Court life, however, brought
Kepler into contact with other prominent scholars (Johannes Matthäus Wackher von Wackhenfels, Jost Bürgi, David Fabricius, Martin Bachazek, and Johannes Brengger, among others) and astronomical work proceeded rapidly.
Astronomiae Pars Optica
A plate from Astronomiae Pars Optica, illustrating the structure of eyes of various species.
As Kepler slowly continued analyzing Tycho's Mars observations—now
available to him in their entirety—and began the slow process of
tabulating the Rudolphine Tables, Kepler also picked up the investigation of the laws of optics from his lunar essay of 1600. Both lunar and solar eclipses
presented unexplained phenomena, such as unexpected shadow sizes, the
red color of a total lunar eclipse, and the reportedly unusual light
surrounding a total solar eclipse. Related issues of atmospheric refraction applied to all
astronomical observations. Through most of 1603, Kepler paused his
other work to focus on optical theory; the resulting manuscript,
presented to the emperor on January 1, 1604, was published as Astronomiae Pars Optica (The Optical Part of Astronomy). In it, Kepler described the inverse-square law governing the intensity of light, reflection by flat and curved mirrors, and principles of pinhole cameras, as well as the astronomical implications of optics such as parallax
and the apparent sizes of heavenly bodies. He also extended his study
of optics to the human eye, and is generally considered by
neuroscientists to be the first to recognize that images are projected
inverted and reversed by the eye's lens onto the retina.
The solution to this dilemma was not of particular importance to Kepler
as he did not see it as pertaining to optics, although he did suggest
that the image was later corrected "in the hollows of the brain" due to
the "activity of the Soul." Today, Astronomiae Pars Optica is generally recognized as the foundation of modern optics (though the law of refraction is conspicuously absent). With respect to the beginnings of projective geometry, Kepler introduced the idea of continuous change of a mathematical entity in this work. He argued that if a focus of a conic section
were allowed to move along the line joining the foci, the geometric
form would morph or degenerate, one into another. In this way, an ellipse becomes a parabola
when a focus moves toward infinity, and when two foci of an ellipse
merge into one another, a circle is formed. As the foci of a hyperbola
merge into one another, the hyperbola becomes a pair of straight lines.
He also assumed that if a straight line is extended to infinity it will
meet itself at a single point at infinity, thus having the properties of a large circle.
Supernova of 1604
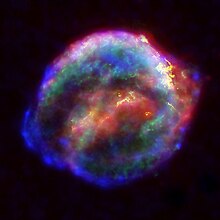
Remnant of Kepler's Supernova SN 1604
In October 1604, a bright new evening star (SN 1604)
appeared, but Kepler did not believe the rumors until he saw it
himself. Kepler began systematically observing the nova. Astrologically,
the end of 1603 marked the beginning of a fiery trigon, the start of the about 800-year cycle of great conjunctions; astrologers associated the two previous such periods with the rise of Charlemagne
(c. 800 years earlier) and the birth of Christ (c. 1600 years earlier),
and thus expected events of great portent, especially regarding the
emperor. It was in this context, as the imperial mathematician and
astrologer to the emperor, that Kepler described the new star two years
later in his De Stella Nova.
In it, Kepler addressed the star's astronomical properties while taking
a skeptical approach to the many astrological interpretations then
circulating. He noted its fading luminosity, speculated about its
origin, and used the lack of observed parallax to argue that it was in
the sphere of fixed stars, further undermining the doctrine of the
immutability of the heavens (the idea accepted since Aristotle that the celestial spheres
were perfect and unchanging). The birth of a new star implied the
variability of the heavens. In an appendix, Kepler also discussed the
recent chronology work of the Polish historian Laurentius Suslyga; he calculated that, if Suslyga was correct that accepted timelines were four years behind, then the Star of Bethlehem—analogous to the present new star—would have coincided with the first great conjunction of the earlier 800-year cycle.
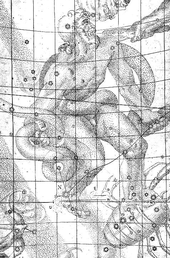
The location of the stella nova, in the foot of Ophiuchus, is marked with an N (8 grid squares down, 4 over from the left).
Astronomia nova
The extended line of research that culminated in Astronomia nova (A New Astronomy)—including the first two laws of planetary motion—began
with the analysis, under Tycho's direction, of Mars' orbit. Kepler
calculated and recalculated various approximations of Mars' orbit using
an equant
(the mathematical tool that Copernicus had eliminated with his system),
eventually creating a model that generally agreed with Tycho's
observations to within two arcminutes
(the average measurement error). But he was not satisfied with the
complex and still slightly inaccurate result; at certain points the
model differed from the data by up to eight arcminutes. The wide array
of traditional mathematical astronomy methods having failed him, Kepler
set about trying to fit an ovoid orbit to the data.
In Kepler's religious view of the cosmos, the Sun (a symbol of God the Father) was the source of motive force in the Solar System. As a physical basis, Kepler drew by analogy on William Gilbert's theory of the magnetic soul of the Earth from De Magnete (1600) and on his own work on optics. Kepler supposed that the motive power (or motive species) radiated by the Sun weakens with distance, causing faster or slower motion as planets move closer or farther from it.
Perhaps this assumption entailed a mathematical relationship that would
restore astronomical order. Based on measurements of the aphelion and perihelion
of the Earth and Mars, he created a formula in which a planet's rate of
motion is inversely proportional to its distance from the Sun.
Verifying this relationship throughout the orbital cycle, however,
required very extensive calculation; to simplify this task, by late 1602
Kepler reformulated the proportion in terms of geometry: planets sweep out equal areas in equal times—Kepler's second law of planetary motion.
Diagram of the geocentric trajectory of Mars through several periods of apparent retrograde motion (Astronomia nova, Chapter 1, 1609)
He then set about calculating the entire orbit of Mars, using the geometrical rate law and assuming an egg-shaped ovoid
orbit. After approximately 40 failed attempts, in early 1605 he at last
hit upon the idea of an ellipse, which he had previously assumed to be
too simple a solution for earlier astronomers to have overlooked. Finding that an elliptical orbit fit the Mars data, he immediately concluded that all planets move in ellipses, with the sun at one focus—Kepler's
first law of planetary motion. Because he employed no calculating
assistants, however, he did not extend the mathematical analysis beyond
Mars. By the end of the year, he completed the manuscript for Astronomia nova,
though it would not be published until 1609 due to legal disputes over
the use of Tycho's observations, the property of his heirs.
Dioptrice, Somnium manuscript, and other work
In the years following the completion of Astronomia Nova, most of Kepler's research was focused on preparations for the Rudolphine Tables and a comprehensive set of ephemerides
(specific predictions of planet and star positions) based on the table
(though neither would be completed for many years). He also attempted
(unsuccessfully) to begin a collaboration with Italian astronomer Giovanni Antonio Magini. Some of his other work dealt with chronology, especially the dating of events in the life of Jesus, and with astrology, especially criticism of dramatic predictions of catastrophe such as those of Helisaeus Roeslin.
Kepler and Roeslin engaged in a series of published attacks and
counter-attacks, while physician Philip Feselius published a work
dismissing astrology altogether (and Roeslin's work in particular). In
response to what Kepler saw as the excesses of astrology on the one hand
and overzealous rejection of it on the other, Kepler prepared Tertius Interveniens
[Third-party Interventions]. Nominally this work—presented to the
common patron of Roeslin and Feselius—was a neutral mediation between
the feuding scholars, but it also set out Kepler's general views on the
value of astrology, including some hypothesized mechanisms of
interaction between planets and individual souls. While Kepler
considered most traditional rules and methods of astrology to be the
"evil-smelling dung" in which "an industrious hen" scrapes, there was an
"occasional grain-seed, indeed, even a pearl or a gold nugget" to be
found by the conscientious scientific astrologer. Conversely, Sir Oliver Lodge
observed that Kepler was somewhat disdainful of astrology, as Kepler
was "continually attacking and throwing sarcasm at astrology, but it was
the only thing for which people would pay him, and on it after a
fashion he lived."
Karlová street in Old Town, Prague – house where Kepler lived. Now a museum
In the first months of 1610, Galileo Galilei—using his powerful new telescope—discovered four satellites orbiting Jupiter. Upon publishing his account as Sidereus Nuncius
[Starry Messenger], Galileo sought the opinion of Kepler, in part to
bolster the credibility of his observations. Kepler responded
enthusiastically with a short published reply, Dissertatio cum Nuncio Sidereo
[Conversation with the Starry Messenger]. He endorsed Galileo's
observations and offered a range of speculations about the meaning and
implications of Galileo's discoveries and telescopic methods, for
astronomy and optics as well as cosmology and astrology. Later that
year, Kepler published his own telescopic observations of the moons in Narratio de Jovis Satellitibus, providing further support of Galileo. To Kepler's disappointment, however, Galileo never published his reactions (if any) to Astronomia Nova.
After hearing of Galileo's telescopic discoveries, Kepler also
started a theoretical and experimental investigation of telescopic
optics using a telescope borrowed from Duke Ernest of Cologne. The resulting manuscript was completed in September 1610 and published as Dioptrice in 1611. In it, Kepler set out the theoretical basis of double-convex converging lenses and double-concave diverging lenses—and how they are combined to produce a Galilean telescope—as well as the concepts of real vs. virtual
images, upright vs. inverted images, and the effects of focal length on
magnification and reduction. He also described an improved
telescope—now known as the astronomical or Keplerian telescope—in which two convex lenses can produce higher magnification than Galileo's combination of convex and concave lenses.
One of the diagrams from Strena Seu de Nive Sexangula, illustrating the Kepler conjecture
Around 1611, Kepler circulated a manuscript of what would eventually be published (posthumously) as Somnium [The Dream]. Part of the purpose of Somnium
was to describe what practicing astronomy would be like from the
perspective of another planet, to show the feasibility of a
non-geocentric system. The manuscript, which disappeared after changing
hands several times, described a fantastic trip to the Moon; it was part
allegory, part autobiography, and part treatise on interplanetary
travel (and is sometimes described as the first work of science
fiction). Years later, a distorted version of the story may have
instigated the witchcraft trial against his mother, as the mother of the
narrator consults a demon to learn the means of space travel. Following
her eventual acquittal, Kepler composed 223 footnotes to the
story—several times longer than the actual text—which explained the
allegorical aspects as well as the considerable scientific content
(particularly regarding lunar geography) hidden within the text.
Work in mathematics and physics
As
a New Year's gift that year (1611), he also composed for his friend and
some-time patron, Baron Wackher von Wackhenfels, a short pamphlet
entitled Strena Seu de Nive Sexangula (A New Year's Gift of Hexagonal Snow).
In this treatise, he published the first description of the hexagonal
symmetry of snowflakes and, extending the discussion into a hypothetical
atomistic physical basis for the symmetry, posed what later became known as the Kepler conjecture, a statement about the most efficient arrangement for packing spheres.
Personal and political troubles
In
1611, the growing political-religious tension in Prague came to a head.
Emperor Rudolph—whose health was failing—was forced to abdicate as King of Bohemia by his brother Matthias.
Both sides sought Kepler's astrological advice, an opportunity he used
to deliver conciliatory political advice (with little reference to the
stars, except in general statements to discourage drastic action).
However, it was clear that Kepler's future prospects in the court of
Matthias were dim.
Also in that year, Barbara Kepler contracted Hungarian spotted fever, then began having seizures.
As Barbara was recovering, Kepler's three children all fell sick with
smallpox; Friedrich, 6, died. Following his son's death, Kepler sent
letters to potential patrons in Württemberg and Padua. At the University of Tübingen in Württemberg, concerns over Kepler's perceived Calvinist heresies in violation of the Augsburg Confession and the Formula of Concord prevented his return. The University of Padua—on
the recommendation of the departing Galileo—sought Kepler to fill the
mathematics professorship, but Kepler, preferring to keep his family in
German territory, instead travelled to Austria to arrange a position as
teacher and district mathematician in Linz. However, Barbara relapsed into illness and died shortly after Kepler's return.
Kepler postponed the move to Linz and remained in Prague until
Rudolph's death in early 1612, though between political upheaval,
religious tension, and family tragedy (along with the legal dispute over
his wife's estate), Kepler could do no research. Instead, he pieced
together a chronology manuscript, Eclogae Chronicae, from
correspondence and earlier work. Upon succession as Holy Roman Emperor,
Matthias re-affirmed Kepler's position (and salary) as imperial
mathematician but allowed him to move to Linz.
Linz and elsewhere (1612–1630)
A statue of Kepler in Linz
In Linz, Kepler's primary responsibilities (beyond completing the Rudolphine Tables)
were teaching at the district school and providing astrological and
astronomical services. In his first years there, he enjoyed financial
security and religious freedom relative to his life in Prague—though he
was excluded from Eucharist
by his Lutheran church over his theological scruples. It was also
during his time in Linz that Kepler had to deal with the accusation and
ultimate verdict of witchcraft against his mother Katharina in the Protestant town of Leonberg. That blow, happening only a few years after Kepler's excommunication, is not seen as a coincidence but as a symptom of the full-fledged assault waged by the Lutherans against Kepler.
His first publication in Linz was De vero Anno (1613), an expanded treatise on the year of Christ's birth; he also participated in deliberations on whether to introduce Pope Gregory's reformed calendar to Protestant German lands; that year he also wrote the influential mathematical treatise Nova stereometria doliorum vinariorum, on measuring the volume of containers such as wine barrels, published in 1615.
Second marriage
On
October 30, 1613, Kepler married the 24-year-old Susanna Reuttinger.
Following the death of his first wife Barbara, Kepler had considered 11
different matches over two years (a decision process formalized later as
the marriage problem).
He eventually returned to Reuttinger (the fifth match) who, he wrote,
"won me over with love, humble loyalty, economy of household, diligence,
and the love she gave the stepchildren."
The first three children of this marriage (Margareta Regina, Katharina,
and Sebald) died in childhood. Three more survived into adulthood:
Cordula (born 1621); Fridmar (born 1623); and Hildebert (born 1625).
According to Kepler's biographers, this was a much happier marriage than
his first.
Epitome of Copernican Astronomy, calendars, and the witch trial of his mother
Kepler's Figure 'M' from the Epitome, showing the world as belonging to just one of any number of similar stars.
Since completing the Astronomia nova, Kepler had intended to compose an astronomy textbook. In 1615, he completed the first of three volumes of Epitome astronomiae Copernicanae (Epitome of Copernican Astronomy);
the first volume (books I–III) was printed in 1617, the second (book
IV) in 1620, and the third (books V–VII) in 1621. Despite the title,
which referred simply to heliocentrism, Kepler's textbook culminated in
his own ellipse-based system. The Epitome became Kepler's most
influential work. It contained all three laws of planetary motion and
attempted to explain heavenly motions through physical causes. Though it explicitly extended the first two laws of planetary motion (applied to Mars in Astronomia nova) to all the planets as well as the Moon and the Medicean satellites of Jupiter, it did not explain how elliptical orbits could be derived from observational data.
As a spin-off from the Rudolphine Tables and the related Ephemerides,
Kepler published astrological calendars, which were very popular and
helped offset the costs of producing his other work—especially when
support from the Imperial treasury was withheld. In his calendars—six
between 1617 and 1624—Kepler forecast planetary positions and weather as
well as political events; the latter were often cannily accurate,
thanks to his keen grasp of contemporary political and theological
tensions. By 1624, however, the escalation of those tensions and the
ambiguity of the prophecies meant political trouble for Kepler himself;
his final calendar was publicly burned in Graz.
Geometrical harmonies in the perfect solids from Harmonices Mundi (1619)
In 1615, Ursula Reingold, a woman in a financial dispute with
Kepler's brother Christoph, claimed Kepler's mother Katharina had made
her sick with an evil brew. The dispute escalated, and in 1617 Katharina
was accused of witchcraft;
witchcraft trials were relatively common in central Europe at this
time. Beginning in August 1620, she was imprisoned for fourteen months.
She was released in October 1621, thanks in part to the extensive legal
defense drawn up by Kepler. The accusers had no stronger evidence than
rumors. Katharina was subjected to territio verbalis, a graphic
description of the torture awaiting her as a witch, in a final attempt
to make her confess. Throughout the trial, Kepler postponed his other
work to focus on his "harmonic theory". The result, published in 1619,
was Harmonices Mundi ("Harmony of the World").
Harmonices Mundi
Kepler was convinced "that the geometrical things have provided the Creator with the model for decorating the whole world". In Harmony,
he attempted to explain the proportions of the natural
world—particularly the astronomical and astrological aspects—in terms of
music. The central set of "harmonies" was the musica universalis or "music of the spheres", which had been studied by Pythagoras, Ptolemy and many others before Kepler; in fact, soon after publishing Harmonices Mundi, Kepler was embroiled in a priority dispute with Robert Fludd, who had recently published his own harmonic theory.
Kepler began by exploring regular polygons and regular solids, including the figures that would come to be known as Kepler's solids.
From there, he extended his harmonic analysis to music, meteorology,
and astrology; harmony resulted from the tones made by the souls of
heavenly bodies—and in the case of astrology, the interaction between
those tones and human souls. In the final portion of the work (Book V),
Kepler dealt with planetary motions, especially relationships between orbital velocity
and orbital distance from the Sun. Similar relationships had been used
by other astronomers, but Kepler—with Tycho's data and his own
astronomical theories—treated them much more precisely and attached new
physical significance to them.
Among many other harmonies, Kepler articulated what came to be
known as the third law of planetary motion. He then tried many
combinations until he discovered that (approximately) "The square of the periodic times are to each other as the cubes of the mean distances."
Although he gives the date of this epiphany (March 8, 1618), he does
not give any details about how he arrived at this conclusion.
However, the wider significance for planetary dynamics of this purely
kinematical law was not realized until the 1660s. When conjoined with Christiaan Huygens' newly discovered law of centrifugal force, it enabled Isaac Newton, Edmund Halley, and perhaps Christopher Wren and Robert Hooke
to demonstrate independently that the presumed gravitational attraction
between the Sun and its planets decreased with the square of the
distance between them.
This refuted the traditional assumption of scholastic physics that the
power of gravitational attraction remained constant with distance
whenever it applied between two bodies, such as was assumed by Kepler
and also by Galileo in his mistaken universal law that gravitational
fall is uniformly accelerated, and also by Galileo's student Borrelli in
his 1666 celestial mechanics.
Rudolphine Tables and his last years
Name "Copernicus" in a manuscript report by Kepler concerning the Rudolphine Tables (1616).
Title page of the Tabulae Rudolphinae, Ulm, 1627
Kepler's horoscope for General Wallenstein
In 1623, Kepler at last completed the Rudolphine Tables,
which at the time was considered his major work. However, due to the
publishing requirements of the emperor and negotiations with Tycho
Brahe's heir, it would not be printed until 1627. In the meantime,
religious tension – the root of the ongoing Thirty Years' War – once again put Kepler and his family in jeopardy. In 1625, agents of the Catholic Counter-Reformation placed most of Kepler's library under seal, and in 1626 the city of Linz was besieged. Kepler moved to Ulm, where he arranged for the printing of the Tables at his own expense.
In 1628, following the military successes of the Emperor Ferdinand's armies under General Wallenstein,
Kepler became an official advisor to Wallenstein. Though not the
general's court astrologer per se, Kepler provided astronomical
calculations for Wallenstein's astrologers and occasionally wrote
horoscopes himself. In his final years, Kepler spent much of his time
traveling, from the imperial court in Prague to Linz and Ulm to a temporary home in Sagan, and finally to Regensburg.
Soon after arriving in Regensburg, Kepler fell ill. He died on November
15, 1630, and was buried there; his burial site was lost after the
Swedish army destroyed the churchyard. Only Kepler's self-authored poetic epitaph survived the times:
- Mensus eram coelos, nunc terrae metior umbras
- Mens coelestis erat, corporis umbra iacet.
- I measured the skies, now the shadows I measure
- Skybound was the mind, earthbound the body rests.
Christianity
Kepler's
belief that God created the cosmos in an orderly fashion caused him to
attempt to determine and comprehend the laws that govern the natural
world, most profoundly in astronomy.
The phrase "I am merely thinking God's thoughts after Him" has been
attributed to him, although this is probably a capsulized version of a
writing from his hand:
Those laws [of nature] are within the grasp of the human mind; God wanted us to recognize them by creating us after his own image so that we could share in his own thoughts.
Reception of his astronomy
Kepler's laws of planetary motion were not immediately accepted. Several major figures such as Galileo and René Descartes completely ignored Kepler's Astronomia nova.
Many astronomers, including Kepler's teacher, Michael Maestlin,
objected to Kepler's introduction of physics into his astronomy. Some
adopted compromise positions. Ismaël Bullialdus
accepted elliptical orbits but replaced Kepler's area law with uniform
motion in respect to the empty focus of the ellipse, while Seth Ward used an elliptical orbit with motions defined by an equant.
Several astronomers tested Kepler's theory, and its various
modifications, against astronomical observations. Two transits of Venus
and Mercury across the face of the sun provided sensitive tests of the
theory, under circumstances when these planets could not normally be
observed. In the case of the transit of Mercury in 1631, Kepler had been
extremely uncertain of the parameters for Mercury, and advised
observers to look for the transit the day before and after the predicted
date. Pierre Gassendi observed the transit on the date predicted, a confirmation of Kepler's prediction. This was the first observation of a transit of Mercury. However, his attempt to observe the transit of Venus
just one month later was unsuccessful due to inaccuracies in the
Rudolphine Tables. Gassendi did not realize that it was not visible from
most of Europe, including Paris. Jeremiah Horrocks, who observed the 1639 Venus transit,
had used his own observations to adjust the parameters of the Keplerian
model, predicted the transit, and then built apparatus to observe the
transit. He remained a firm advocate of the Keplerian model.
Epitome of Copernican Astronomy was read by astronomers
throughout Europe, and following Kepler's death, it was the main vehicle
for spreading Kepler's ideas. In the period 1630 – 1650, this book was
the most widely used astronomy textbook, winning many converts to
ellipse-based astronomy.
However, few adopted his ideas on the physical basis for celestial
motions. In the late 17th century, a number of physical astronomy
theories drawing from Kepler's work—notably those of Giovanni Alfonso Borelli
and Robert Hooke—began to incorporate attractive forces (though not the
quasi-spiritual motive species postulated by Kepler) and the Cartesian
concept of inertia. This culminated in Isaac Newton's Principia Mathematica (1687), in which Newton derived Kepler's laws of planetary motion from a force-based theory of universal gravitation.
Historical and cultural legacy
Monument to Tycho Brahe and Kepler in Prague, Czech Republic
The GDR stamp featuring Kepler
History of science
Beyond his role in the historical development of astronomy and natural philosophy, Kepler has loomed large in the philosophy and historiography of science. Kepler and his laws of motion were central to early histories of astronomy such as Jean-Étienne Montucla's 1758 Histoire des mathématiques and Jean-Baptiste Delambre's 1821 Histoire de l'astronomie moderne. These and other histories written from an Enlightenment perspective treated Kepler's metaphysical and religious arguments with skepticism and disapproval, but later Romantic-era natural philosophers viewed these elements as central to his success.
William Whewell, in his influential History of the Inductive Sciences of 1837, found Kepler to be the archetype of the inductive scientific genius; in his Philosophy of the Inductive Sciences of 1840, Whewell held Kepler up as the embodiment of the most advanced forms of scientific method. Similarly, Ernst Friedrich Apelt—the first to extensively study Kepler's manuscripts, after their purchase by Catherine the Great—identified Kepler as a key to the "Revolution of the sciences".
Apelt, who saw Kepler's mathematics, aesthetic sensibility, physical
ideas, and theology as part of a unified system of thought, produced the
first extended analysis of Kepler's life and work.
Alexandre Koyré's
work on Kepler was, after Apelt, the first major milestone in
historical interpretations of Kepler's cosmology and its influence. In
the 1930s and 1940s, Koyré, and a number of others in the first
generation of professional historians of science, described the "Scientific Revolution"
as the central event in the history of science, and Kepler as a
(perhaps the) central figure in the revolution. Koyré placed Kepler's
theorization, rather than his empirical work, at the center of the
intellectual transformation from ancient to modern world-views. Since
the 1960s, the volume of historical Kepler scholarship has expanded
greatly, including studies of his astrology and meteorology, his
geometrical methods, the role of his religious views in his work, his
literary and rhetorical methods, his interaction with the broader
cultural and philosophical currents of his time, and even his role as an
historian of science.
Philosophers of science—such as Charles Sanders Peirce, Norwood Russell Hanson, Stephen Toulmin, and Karl Popper—have repeatedly turned to Kepler: examples of incommensurability, analogical reasoning, falsification, and many other philosophical concepts have been found in Kepler's work. Physicist Wolfgang Pauli even used Kepler's priority dispute with Robert Fludd to explore the implications of analytical psychology on scientific investigation.
Editions and translations
Modern
translations of a number of Kepler's books appeared in the
late-nineteenth and early-twentieth centuries, the systematic
publication of his collected works began in 1937 (and is nearing
completion in the early 21st century).
An edition in eight volumes, Kepleri Opera omnia, was prepared by Christian Frisch (1807–1881), during 1858 to 1871, on the occasion of Kepler's 300th birthday.
Frisch's edition only included Kepler's Latin, with a Latin commentary.
A new edition was planned beginning in 1914 by Walther von Dyck
(1856–1934). Dyck compiled copies of Kepler's unedited manuscripts,
using international diplomatic contacts to convince the Soviet
authorities to lend him the manuscripts kept in Leningrad for
photographic reproduction. These manuscripts contained several works by
Kepler that had not been available to Frisch. Dyck's photographs remain
the basis for the modern editions of Kepler's unpublished manuscripts.
Max Caspar (1880–1956) published his German translation of Kepler's Mysterium Cosmographicum in 1923.
Both Dyck and Caspar were influenced in their interest in Kepler by mathematician Alexander von Brill (1842–1935).
Caspar became Dyck's collaborator, succeeding him as project leader in 1934, establishing the Kepler-Kommission
in the following year. Assisted by Martha List (1908–1992) and Franz
Hammer (1898–1979), Caspar continued editorial work during World War II.
Max Caspar also published a biography of Kepler in 1948. The commission was later chaired by Volker Bialas (during 1976–2003) and Ulrich Grigull (during 1984–1999) and Roland Bulirsch (1998–2014).
Popular science and historical fiction
Kepler has acquired a popular image as an icon of scientific modernity and a man before his time; science popularizer Carl Sagan described him as "the first astrophysicist and the last scientific astrologer".
The debate over Kepler's place in the Scientific Revolution has
produced a wide variety of philosophical and popular treatments. One of
the most influential is Arthur Koestler's 1959 The Sleepwalkers, in which Kepler is unambiguously the hero (morally and theologically as well as intellectually) of the revolution.
A well-received, if fanciful, historical novel by John Banville, Kepler (1981), explored many of the themes developed in Koestler's non-fiction narrative and in the philosophy of science.
Somewhat more fanciful is a recent work of nonfiction, Heavenly Intrigue (2004), suggesting that Kepler murdered Tycho Brahe to gain access to his data.
Veneration and eponymy
In Austria, Kepler left behind such a historical legacy that he was one of the motifs of a silver collector's coin: the 10-euro Johannes Kepler silver coin,
minted on September 10, 2002. The reverse side of the coin has a
portrait of Kepler, who spent some time teaching in Graz and the
surrounding areas. Kepler was acquainted with Prince Hans Ulrich von Eggenberg personally, and he probably influenced the construction of Eggenberg Castle (the motif of the obverse of the coin). In front of him on the coin is the model of nested spheres and polyhedra from Mysterium Cosmographicum.
The German composer Paul Hindemith wrote an opera about Kepler entitled Die Harmonie der Welt, and a symphony of the same name was derived from music for the opera.
Philip Glass wrote an opera called Kepler based on Kepler's life (2009).
Kepler is honored together with Nicolaus Copernicus with a feast day on the liturgical calendar of the Episcopal Church (USA) on May 23.
Directly named for Kepler's contribution to science are Kepler's laws of planetary motion, Kepler's Supernova (Supernova 1604, which he observed and described) and the Kepler Solids, a set of geometrical constructions, two of which were described by him, and the Kepler conjecture on sphere packing.
The Kepler crater as photographed by Apollo 12 in 1969
- In astronomy: The lunar crater Kepler (Keplerus, named by Giovanni Riccioli, 1651), the asteroid 1134 Kepler (1929), Kepler (crater on Mars) (1973), Kepler Launch Site for model rockets (2001), the Kepler space telescope, a space photometer launched by NASA in 2009, Johannes Kepler ATV (Automated Transfer Vehicle launched to resupply the ISS in 2011).
- Educational institutions: Johannes Kepler University Linz (1975), Kepler College (Seattle, Washington), besides several institutions of primary and secondary education, such as Johannes Kepler Grammar School, at the site where Kepler lived in Prague, and Kepler Gymnasium, Tübingen
- Streets or squares named after him: Keplerplatz Vienna (station of Vienna U-Bahn), Keplerstraße in Hanau near Frankfurt am Main, Keplerstraße in Munich, Germany, Keplerstraße and Keplerbrücke in Graz, Austria, Keplerova ulice in Prague.
- The Kepler Mountains and Kepler Track in Fiordland National Park, South Island, New Zealand; Kepler Challenge (1988).
- Kepler, a high end graphics processing microarchitecture introduced by Nvidia in 2012.
Works
- Epitome astronomiae copernicanae, 1618
- Harmonices Mundi (Harmony of the Worlds) (1619) (English translation on Google Books)
- Mysterium cosmographicum (The Sacred Mystery of the Cosmos), 2nd edition (1621)
- Tabulae Rudolphinae (Rudolphine Tables) (1627)
- Somnium (The Dream) (1634) (English translation on Google Books preview)
- Vol. 1: Mysterium Cosmographicum. De Stella Nova. Ed. M. Caspar. 1938, 2nd ed. 1993. Paperback ISBN 3-406-01639-1.
- Vol. 2: Astronomiae pars optica. Ed. F. Hammer. 1939, Paperback ISBN 3-406-01641-3.
- Vol. 3: Astronomia Nova. Ed. M. Caspar. 1937. IV, 487 p. 2. ed. 1990. Paperback ISBN 3-406-01643-X. Semi-parchment ISBN 3-406-01642-1.
- Vol. 4: Kleinere Schriften 1602–1611. Dioptrice. Ed. M. Caspar, F. Hammer. 1941. ISBN 3-406-01644-8.
- Vol. 5: Chronologische Schriften. Ed. F. Hammer. 1953. Out-of-print.
- Vol. 6: Harmonice Mundi. Ed. M. Caspar. 1940, 2nd ed. 1981, ISBN 3-406-01648-0.
- Vol. 7: Epitome Astronomiae Copernicanae. Ed. M. Caspar. 1953, 2nd ed. 1991. ISBN 3-406-01650-2, Paperback ISBN 3-406-01651-0.
- Vol. 8: Mysterium Cosmographicum. Editio altera cum notis. De Cometis. Hyperaspistes. Commentary F. Hammer. 1955. Paperback ISBN 3-406-01653-7.
- Vol 9: Mathematische Schriften. Ed. F. Hammer. 1955, 2nd ed. 1999. Out-of-print.
- Vol. 10: Tabulae Rudolphinae. Ed. F. Hammer. 1969. ISBN 3-406-01656-1.
- Vol. 11,1: Ephemerides novae motuum coelestium. Commentary V. Bialas. 1983. ISBN 3-406-01658-8, Paperback ISBN 3-406-01659-6.
- Vol. 11,2: Calendaria et Prognostica. Astronomica minora. Somnium. Commentary V. Bialas, H. Grössing. 1993. ISBN 3-406-37510-3, Paperback ISBN 3-406-37511-1.
- Vol. 12: Theologica. Hexenprozeß. Tacitus-Übersetzung. Gedichte. Commentary J. Hübner, H. Grössing, F. Boockmann, F. Seck. Directed by V. Bialas. 1990. ISBN 3-406-01660-X, Paperback ISBN 3-406-01661-8.
- Vols. 13–18: Letters:
-
- Vol. 13: Briefe 1590–1599. Ed. M. Caspar. 1945. 432 p. ISBN 3-406-01663-4.
- Vol. 14: Briefe 1599–1603. Ed. M. Caspar. 1949. Out-of-print. 2nd ed. in preparation.
- Vol 15: Briefe 1604–1607. Ed. M. Caspar. 1951. 2nd ed. 1995. ISBN 3-406-01667-7.
- Vol. 16: Briefe 1607–1611. Ed. M. Caspar. 1954. ISBN 3-406-01668-5.
- Vol. 17: Briefe 1612–1620. Ed. M. Caspar. 1955. ISBN 3-406-01671-5.
- Vol. 18: Briefe 1620–1630. Ed. M. Caspar. 1959. ISBN 3-406-01672-3.
- Vol. 19: Dokumente zu Leben und Werk. Commentary M. List. 1975. ISBN 978-3-406-01674-5.
- Vols. 20–21: manuscripts
- Vol. 20,1: Manuscripta astronomica (I). Apologia, De motu Terrae, Hipparchus etc. Commentary V. Bialas. 1988. ISBN 3-406-31501-1. Paperback ISBN 3-406-31502-X.
- Vol. 20,2: Manuscripta astronomica (II). Commentaria in Theoriam Martis. Commentary V. Bialas. 1998. Paperback ISBN 3-406-40593-2.
- Vol. 21,1: Manuscripta astronomica (III) et mathematica. De Calendario Gregoriano. In preparation.
- Vol. 21,2: Manuscripta varia. In preparation.
- Vol. 22: General index, in preparation.