Criminal justice

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Criminal_justice 

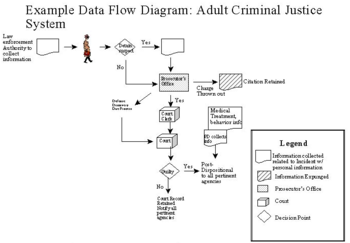
United States criminal justice system flowchart.

Criminal justice is the delivery of justice to those who have committed crimes. The criminal justice system is a series of government agencies and institutions. Goals include the rehabilitation of offenders, preventing other crimes, and moral support for victims. The primary institutions of the criminal justice system are the police, prosecution and defense lawyers, the courts and prisons.

Law

The Law From Old English lagu (something laid down or fixed) (Harper, Douglas. "law". Online Etymology Dictionary.); legal comes from Latin legalis, from lex "law," "statute" (Harper, Douglas. "legal". Online Etymology Dictionary.) is a system of rules usually enforced through a set of institutions. The purpose of law is to provide an objective set of rules for governing conduct and maintaining order in a society.

The oldest known codified law is the Code of Hammurabi, dating back to about 1754 BC. The preface directly credits the laws to the Code of Hammurabi of Ur. In different parts of the world, law could be established by philosophers or religion. In the modern world, laws are typically created and enforced by governments. These codified laws may coexist with or contradict other forms of social control, such as religious proscriptions, professional rules and ethics, or the cultural mores and customs of a society.

Within the realm of codified law, there are generally two forms of law that the courts are concerned with. Civil laws are rules and regulations which govern transactions and grievances between individual citizens. Criminal law is concerned with actions which are dangerous or harmful to society as a whole, in which prosecution is pursued not by an individual but rather by the state. The purpose of criminal law is to provide the specific definition of what constitutes a crime and to prescribe punishments for committing such a crime. No criminal law can be valid unless it includes both of these factors. The subject of criminal justice is, of course, primarily concerned with the enforcement of criminal law.

Criminal-justice system

Definition

The criminal-justice system consists of three main parts:

1. Law enforcement agencies, usually the police
2. Courts and accompanying prosecution and defence lawyers
3. Agencies for detaining and supervising offenders, such as prisons and probation agencies.

In the criminal justice system, these distinct agencies operate together as the principal means of maintaining the rule of law within society.

This image shows the procedure in the criminal justice system

Law enforcement

The first contact a defendant has with the criminal justice system is usually with the police (or law enforcement) who investigates the suspected wrongdoing and makes an arrest, but if the suspect is dangerous to the whole nation, a national level law enforcement agency is called in. When warranted, law enforcement agencies or police officers are empowered to use force and other forms of legal coercion and means to effect public and social order. The term is most commonly associated with police departments of a state that are authorized to exercise the police power of that state within a defined legal or territorial area of responsibility. The word comes from the Latin politia ("civil administration"), which itself derives from the Ancient Greek πόλις, for polis ("city"). The first police force comparable to the present-day police was established in 1667 under King Louis XIV in France, although modern police usually trace their origins to the 1800 establishment of the Marine Police in London, the Glasgow Police, and the Napoleonic police of Paris.

Police are primarily concerned with keeping the peace and enforcing criminal law based on their particular mission and jurisdiction. Formed in 1908, the Federal Bureau of Investigation began as an entity which could investigate and enforce specific federal laws as an investigative and "law enforcement agency" in the United States; this, however, has constituted only a small portion of overall policing activity. Policing has included an array of activities in different contexts, but the predominant ones are concerned with order maintenance and the provision of services. During modern times, such endeavors contribute toward fulfilling a shared mission among law enforcement organizations with respect to the traditional policing mission of deterring crime and maintaining societal order.

Courts

A trial at the Old Bailey in London, c. 1808

 

The courts serve as the venue where disputes are then settled and justice is administered. With regard to criminal justice, there are a number of critical people in any court setting. These critical people are referred to as the courtroom work group and include both professional and non professional individuals. These include the judge, prosecutor, and the defense attorney. The judge, or magistrate, is a person, elected or appointed, who is knowledgeable in the law, and whose function is to objectively administer the legal proceedings and offer a final decision to dispose of a case. 

In the U.S. and in a growing number of nations, guilt or innocence (although in the U.S. a jury can never find a defendant "innocent" but rather "not guilty") is decided through the adversarial system. In this system, two parties will both offer their version of events and argue their case before the court (sometimes before a judge or panel of judges, sometimes before a jury). The case should be decided in favor of the party who offers the most sound and compelling arguments based on the law as applied to the facts of the case.

The prosecutor, or district attorney, is a lawyer who brings charges against a person, persons or corporate entity. It is the prosecutor's duty to explain to the court what crime was committed and to detail what evidence has been found which incriminates the accused. The prosecutor should not be confused with a plaintiff or plaintiff's counsel. Although both serve the function of bringing a complaint before the court, the prosecutor is a servant of the state who makes accusations on behalf of the state in criminal proceedings, while the plaintiff is the complaining party in civil proceedings.

A defense attorney counsels the accused on the legal process, likely outcomes for the accused and suggests strategies. The accused, not the lawyer, has the right to make final decisions regarding a number of fundamental points, including whether to testify, and to accept a plea offer or demand a jury trial in appropriate cases. It is the defense attorney's duty to represent the interests of the client, raise procedural and evidentiary issues, and hold the prosecution to its burden of proving guilt beyond a reasonable doubt. Defense counsel may challenge evidence presented by the prosecution or present exculpatory evidence and argue on behalf of their client. At trial, the defense attorney may attempt to offer a rebuttal to the prosecutor's accusations.

In the U.S., an accused person is entitled to a government-paid defense attorney if he or she is in jeopardy of losing his or her life and/or liberty. Those who cannot afford a private attorney may be provided one by the state. Historically, however, the right to a defense attorney has not always been universal. For example, in Tudor England criminals accused of treason were not permitted to offer arguments in their defense. In many jurisdictions, there is no right to an appointed attorney, if the accused is not in jeopardy of losing his or her liberty.

The final determination of guilt or innocence is typically made by a third party, who is supposed to be disinterested. This function may be performed by a judge, a panel of judges, or a jury panel composed of unbiased citizens. This process varies depending on the laws of the specific jurisdiction. In some places the panel (be it judges or a jury) is required to issue a unanimous decision, while in others only a majority vote is required. In America, this process depends on the state, level of court, and even agreements between the prosecuting and defending parties. Some nations do not use juries at all, or rely on theological or military authorities to issue verdicts.

Some cases can be disposed of without the need for a trial. In fact, the vast majority are. If the accused confesses his or her guilt, a shorter process may be employed and a judgment may be rendered more quickly. Some nations, such as America, allow plea bargaining in which the accused pleads guilty, nolo contendere or not guilty, and may accept a diversion program or reduced punishment, where the prosecution's case is weak or in exchange for the cooperation of the accused against other people. This reduced sentence is sometimes a reward for sparing the state the expense of a formal trial. Many nations do not permit the use of plea bargaining, believing that it coerces innocent people to plead guilty in an attempt to avoid a harsh punishment. The courts nowadays are seeking alternative measures as opposed to throwing someone into prison right away.

The entire trial process, whatever the country, is fraught with problems and subject to criticism. Bias and discrimination form an ever-present threat to an objective decision. Any prejudice on the part of the lawyers, the judge, or jury members threatens to destroy the court's credibility. Some people argue that the often Byzantine rules governing courtroom conduct and processes restrict a layman's ability to participate, essentially reducing the legal process to a battle between the lawyers. In this case, the criticism is that the decision is based less on sound justice and more on the lawyer's eloquence and charisma. This is a particular problem when the lawyer performs in a substandard manner. The jury process is another area of frequent criticism, as there are few mechanisms to guard against poor judgment or incompetence on the part of the layman jurors. Judges themselves are very subject to bias subject to things as ordinary as the length of time since their last break.

Manipulations of the court system by defense and prosecution attorneys, law enforcement as well as the defendants have occurred and there have been cases where justice was denied.

Corrections and rehabilitation

The Huntsville Unit of the Texas Department of Criminal Justice in Huntsville, Texas is a prison, a component of a corrections system

Offenders are then turned over to the correctional authorities, from the court system after the accused has been found guilty. Like all other aspects of criminal justice, the administration of punishment has taken many different forms throughout history. Early on, when civilizations lacked the resources necessary to construct and maintain prisons, exile and execution were the primary forms of punishment. Historically shame punishments and exile have also been used as forms of censure.

The most publicly visible form of punishment in the modern era is the prison. Prisons may serve as detention centers for prisoners after trial. For containment of the accused, jails are used. Early prisons were used primarily to sequester criminals and little thought was given to living conditions within their walls. In America, the Quaker movement is commonly credited with establishing the idea that prisons should be used to reform criminals. This can also be seen as a critical moment in the debate regarding the purpose of punishment.

Qur'anic education for offenders at the Central Jail Faisalabad in Faisalabad, Pakistan

 

Punishment (in the form of prison time) may serve a variety of purposes. First, and most obviously, the incarceration of criminals removes them from the general population and inhibits their ability to perpetrate further crimes. A new goal of prison punishments is to offer criminals a chance to be rehabilitated. Many modern prisons offer schooling or job training to prisoners as a chance to learn a vocation and thereby earn a legitimate living when they are returned to society. Religious institutions also have a presence in many prisons, with the goal of teaching ethics and instilling a sense of morality in the prisoners. If a prisoner is released before his time is served, he is released as a parole. This means that they are released, but the restrictions are greater than that of someone on probation.

There are numerous other forms of punishment which are commonly used in conjunction with or in place of prison terms. Monetary fines are one of the oldest forms of punishment still used today. These fines may be paid to the state or to the victims as a form of reparation. Probation and house arrest are also sanctions which seek to limit a person's mobility and his or her opportunities to commit crimes without actually placing them in a prison setting. Furthermore, many jurisdictions may require some form of public or community service as a form of reparations for lesser offenses. In Corrections, the Department ensures court-ordered, pre-sentence chemical dependency assessments, related Drug Offender Sentencing Alternative specific examinations and treatment will occur for offenders sentenced to Drug Offender Sentencing Alternative in compliance with RCW 9.94A.660.

Execution or capital punishment is still used around the world. Its use is one of the most heavily debated aspects of the criminal justice system. Some societies are willing to use executions as a form of political control, or for relatively minor misdeeds. Other societies reserve execution for only the most sinister and brutal offenses. Others still have discontinued the practice entirely, accepting the use of execution to be excessively cruel and/or irreversible in case of an erroneous conviction.

Academic discipline

The functional study of criminal justice is distinct from criminology, which involves the study of crime as a social phenomenon, causes of crime, criminal behavior, and other aspects of crime. It emerged as an academic discipline in the 1920s, beginning with Berkeley police chief August Vollmer who established a criminal justice program at the University of California, Berkeley in 1916. Vollmer's work was carried on by his student, O.W. Wilson, who led efforts to professionalize policing and reduce corruption. Other programs were established in the United States at Indiana University, Michigan State University, San Jose State University, and the University of Washington. As of 1950, criminal justice students were estimated to number less than 1,000. Until the 1960s, the primary focus of criminal justice in the United States was on policing and police science.

Throughout the 1960s and 1970s, crime rates soared and social issues took center stage in the public eye. A number of new laws and studies focused federal resources on researching new approaches to crime control. The Warren Court (the Supreme Court under Chief Justice Earl Warren), issued a series of rulings which redefined citizen's rights and substantially altered the powers and responsibilities of police and the courts. The Civil Rights Era offered significant legal and ethical challenges to the status quo.

In the late 1960s, with the establishment of the Law Enforcement Assistance Administration (LEAA) and associated policy changes that resulted with the Omnibus Crime Control and Safe Streets Act of 1968. The LEAA provided grants for criminology research, focusing on social aspects of crime. By the 1970s, there were 729 academic programs in criminology and criminal justice in the United States. Largely thanks to the Law Enforcement Education Program, criminal justice students numbered over 100,000 by 1975. Over time, scholars of criminal justice began to include criminology, sociology, and psychology, among others, to provide a more comprehensive view of the criminal justice system and the root causes of crime. Criminal justice studies now combine the practical and technical policing skills with a study of social deviance as a whole.

Criminal justice degree programs at four-year institutions typically include coursework in statistics, methods of research, criminal justice, policing, U.S court systems, criminal courts, corrections, community corrections, criminal procedure, criminal law, victimology, juvenile justice, and a variety of special topics. A number of universities offer a Bachelor of Criminal Justice.

History

Prisoners at a whipping post in a Delaware prison, c. 1907

The modern criminal justice system has evolved since ancient times, with new forms of punishment, added rights for offenders and victims, and policing reforms. These developments have reflected changing customs, political ideals, and economic conditions. In ancient times through the Middle Ages, exile was a common form of punishment. During the Middle Ages, payment to the victim (or the victim's family), known as wergild, was another common punishment, including for violent crimes. For those who could not afford to buy their way out of punishment, harsh penalties included various forms of corporal punishment. These included mutilation, branding, and flogging, as well as execution.

Though a prison, Le Stinche, existed as early as the 14th century in Florence, Italy, incarceration was not widely used until the 19th century. Correctional reform in the United States was first initiated by William Penn, towards the end of the 17th century. For a time, Pennsylvania's criminal code was revised to forbid torture and other forms of cruel punishment, with jails and prisons replacing corporal punishment. These reforms were reverted, upon Penn's death in 1718. Under pressure from a group of Quakers, these reforms were revived in Pennsylvania toward the end of the 18th century, and led to a marked drop in Pennsylvania's crime rate. Patrick Colquhoun, Henry Fielding and others led significant reforms during the late eighteenth and early nineteenth centuries.

The first official criminal justice system was created by the British during the American Revolution, as they created the system to primarily justify hangings to the citizens of their government. In each selected area or/and district there was a magistrate that in today's time would be known as a judge. These individuals were in charge of determining if the Crown or also known as the British government had enough evidence to hang an individual for a crime. The British would not always hang an individual for committing a crime, there would also be trials for punishments that would be carried out by cleaning ships, prison ships, or be locked up on British mainland. During the American revolution the primary type of punishment was to be hanged or sent to prison ships such as the notorious HMS Jersey. After the American revolution the British-based criminal justice system was then adopted by other developing nations (Such as the United States).

Modern police

The first modern police force is commonly said to be the Metropolitan Police in London, established in 1829 by Sir Robert Peel. Based on the Peelian principles, it promoted the preventive role of police as a deterrent to urban crime and disorder. In the United States, police departments were first established in Boston in 1838, and New York City in 1844. Early on, police were not respected by the community, as corruption was rampant. 

In the 1920s, led by Berkeley, California police chief, August Vollmer and O.W. Wilson, police began to professionalize, adopt new technologies, and place emphasis on training and professional qualifications of new hires. Despite such reforms, police agencies were led by highly autocratic leaders, and there remained a lack of respect between police and the community. Following urban unrest in the 1960s, police placed more emphasis on community relations, enacted reforms such as increased diversity in hiring, and many police agencies adopted community policing strategies.

In the 1990s, CompStat was developed by the New York Police Department as an information-based system for tracking and mapping crime patterns and trends, and holding police accountable for dealing with crime problems. CompStat has since been replicated in police departments across the United States and around the world, with problem-oriented policing, intelligence-led policing, and other information-led policing strategies also adopted.

Graph theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Graph_theory 

A drawing of a graph.

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically; see Graph (discrete mathematics) for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.

Refer to the glossary of graph theory for basic definitions in graph theory.

Definitions

Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures.

Graph

A graph with three vertices and three edges.

In one restricted but very common sense of the term, a graph is an ordered pair G = (V, E) comprising:

• V a set of vertices (also called nodes or points);
• E ⊆ {{x, y} | (x, y) ∈ V² ∧ x ≠ y} a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with two distinct vertices).

To avoid ambiguity, this type of object may be called precisely an undirected simple graph.

In the edge {x, y}, the vertices x and y are called the endpoints of the edge. The edge is said to join x and y and to be incident on x and on y. A vertex may exist in a graph and not belong to an edge. Multiple edges are two or more edges that join the same two vertices.

In one more general sense of the term allowing multiple edges,^[3][4] a graph is an ordered triple G = (V, E, ϕ) comprising:

• V a set of vertices (also called nodes or points);
• E a set of edges (also called links or lines);
• ϕ: E → {{x, y} | (x, y) ∈ V² ∧ x ≠ y} an incidence function mapping every edge to an unordered pair of vertices (that is, an edge is associated with two distinct vertices).

To avoid ambiguity, this type of object may be called precisely an undirected multigraph.

A loop is an edge that joins a vertex to itself. Graphs as defined in the two definitions above cannot have loops, because a loop joining a vertex x is the edge (for an undirected simple graph) or is incident on (for an undirected multigraph) {x, x} = {x} which is not in {{x, y} | (x, y) ∈ V² ∧ x ≠ y}. So to allow loops the definitions must be expanded. For undirected simple graphs, E ⊆ {{x, y} | (x, y) ∈ V² ∧ x ≠ y} should become E ⊆ {{x, y} | (x, y) ∈ V²}. For undirected multigraphs, ϕ: E → {{x, y} | (x, y) ∈ V² ∧ x ≠ y} should become ϕ: E → {{x, y} | (x, y) ∈ V²}. To avoid ambiguity, these types of objects may be called precisely an undirected simple graph permitting loops and an undirected multigraph permitting loops respectively.

V and E are usually taken to be finite, and many of the well-known results are not true (or are rather different) for infinite graphs because many of the arguments fail in the infinite case. Moreover, V is often assumed to be non-empty, but E is allowed to be the empty set. The order of a graph is |V|, its number of vertices. The size of a graph is |E|, its number of edges. The degree or valency of a vertex is the number of edges that are incident to it, where a loop is counted twice.

In an undirected simple graph of order n, the maximum degree of each vertex is n − 1 and the maximum size of the graph is n(n − 1)/2.

The edges of an undirected simple graph permitting loops G induce a symmetric homogeneous relation ~ on the vertices of G that is called the adjacency relation of G. Specifically, for each edge {x, y}, its endpoints x and y are said to be adjacent to one another, which is denoted x ~ y.

Directed graph

A directed graph with three vertices and four directed edges (the double arrow represents an edge in each direction).

A directed graph or digraph is a graph in which edges have orientations. 

In one restricted but very common sense of the term, a directed graph is an ordered pair G = (V, E) comprising:

• V a set of vertices (also called nodes or points);
• E ⊆ {(x, y) | (x, y) ∈ V² ∧ x ≠ y} a set of edges (also called directed edges, directed links, directed lines, arrows or arcs) which are ordered pairs of distinct vertices (i.e., an edge is associated with two distinct vertices).

To avoid ambiguity, this type of object may be called precisely a directed simple graph.

In the edge (x, y) directed from x to y, the vertices x and y are called the endpoints of the edge, x the tail of the edge and y the head of the edge. The edge (y, x) is called the inverted edge of (x, y). The edge is said to join x and y and to be incident on x and on y. A vertex may exist in a graph and not belong to an edge. Multiple edges are two or more edges with both the same tail and the same head.

In one more general sense of the term allowing multiple edges, a directed graph is an ordered triple G = (V, E, ϕ) comprising:

• V a set of vertices (also called nodes or points);
• E a set of edges (also called directed edges, directed links, directed lines, arrows or arcs);
• ϕ: E → {(x, y) | (x, y) ∈ V² ∧ x ≠ y} an incidence function mapping every edge to an ordered pair of distinct vertices (i.e., an edge is associated with two distinct vertices).

To avoid ambiguity, this type of object may be called precisely a directed multigraph. 

A loop is an edge that joins a vertex to itself. Directed graphs as defined in the two definitions above cannot have loops, because a loop joining a vertex x is the edge (for a directed simple graph) or is incident on (for a directed multigraph) (x, x) which is not in {(x, y) | (x, y) ∈ V² ∧ x ≠ y}. So to allow loops the definitions must be expanded. For directed simple graphs, E ⊆ {(x, y) | (x, y) ∈ V² ∧ x ≠ y} should become E ⊆ {(x, y) | (x, y) ∈ V²}. For directed multigraphs, ϕ: E → {(x, y) | (x, y) ∈ V² ∧ x ≠ y} should become ϕ: E → {(x, y) | (x, y) ∈ V²}. To avoid ambiguity, these types of objects may be called precisely a directed simple graph permitting loops and a directed multigraph permitting loops (or a quiver) respectively.

The edges of a directed simple graph permitting loops G is a homogeneous relation ~ on the vertices of G that is called the adjacency relation of G. Specifically, for each edge (x, y), its endpoints x and y are said to be adjacent to one another, which is denoted x ~ y.

Applications

The network graph formed by Wikipedia editors (edges) contributing to different Wikipedia language versions (vertices) during one month in summer 2013.

 

Graphs can be used to model many types of relations and processes in physical, biological, social and information systems. Many practical problems can be represented by graphs. Emphasizing their application to real-world systems, the term network is sometimes defined to mean a graph in which attributes (e.g. names) are associated with the vertices and edges, and the subject that expresses and understands the real-world systems as a network is called network science.

Computer science

In computer science, graphs are used to represent networks of communication, data organization, computational devices, the flow of computation, etc. For instance, the link structure of a website can be represented by a directed graph, in which the vertices represent web pages and directed edges represent links from one page to another. A similar approach can be taken to problems in social media, travel, biology, computer chip design, mapping the progression of neuro-degenerative diseases, and many other fields. The development of algorithms to handle graphs is therefore of major interest in computer science. The transformation of graphs is often formalized and represented by graph rewrite systems. Complementary to graph transformation systems focusing on rule-based in-memory manipulation of graphs are graph databases geared towards transaction-safe, persistent storing and querying of graph-structured data.

Linguistics

Graph-theoretic methods, in various forms, have proven particularly useful in linguistics, since natural language often lends itself well to discrete structure. Traditionally, syntax and compositional semantics follow tree-based structures, whose expressive power lies in the principle of compositionality, modeled in a hierarchical graph. More contemporary approaches such as head-driven phrase structure grammar model the syntax of natural language using typed feature structures, which are directed acyclic graphs. Within lexical semantics, especially as applied to computers, modeling word meaning is easier when a given word is understood in terms of related words; semantic networks are therefore important in computational linguistics. Still, other methods in phonology (e.g. optimality theory, which uses lattice graphs) and morphology (e.g. finite-state morphology, using finite-state transducers) are common in the analysis of language as a graph. Indeed, the usefulness of this area of mathematics to linguistics has borne organizations such as TextGraphs, as well as various 'Net' projects, such as WordNet, VerbNet, and others.

Physics and chemistry

Graph theory is also used to study molecules in chemistry and physics. In condensed matter physics, the three-dimensional structure of complicated simulated atomic structures can be studied quantitatively by gathering statistics on graph-theoretic properties related to the topology of the atoms. Also, "the Feynman graphs and rules of calculation summarize quantum field theory in a form in close contact with the experimental numbers one wants to understand." In chemistry a graph makes a natural model for a molecule, where vertices represent atoms and edges bonds. This approach is especially used in computer processing of molecular structures, ranging from chemical editors to database searching. In statistical physics, graphs can represent local connections between interacting parts of a system, as well as the dynamics of a physical process on such systems. Similarly, in computational neuroscience graphs can be used to represent functional connections between brain areas that interact to give rise to various cognitive processes, where the vertices represent different areas of the brain and the edges represent the connections between those areas. Graph theory plays an important role in electrical modeling of electrical networks, here, weights are associated with resistance of the wire segments to obtain electrical properties of network structures. Graphs are also used to represent the micro-scale channels of porous media, in which the vertices represent the pores and the edges represent the smaller channels connecting the pores. Chemical graph theory uses the molecular graph as a means to model molecules. Graphs and networks are excellent models to study and understand phase transitions and critical phenomena. Removal of nodes or edges lead to a critical transition where the network breaks into small clusters which is studied as a phase transition. This breakdown is studied via percolation theory.

Social sciences

Graph theory in sociology: Moreno Sociogram (1953).

 

Graph theory is also widely used in sociology as a way, for example, to measure actors' prestige or to explore rumor spreading, notably through the use of social network analysis software. Under the umbrella of social networks are many different types of graphs. Acquaintanceship and friendship graphs describe whether people know each other. Influence graphs model whether certain people can influence the behavior of others. Finally, collaboration graphs model whether two people work together in a particular way, such as acting in a movie together.

Biology

Likewise, graph theory is useful in biology and conservation efforts where a vertex can represent regions where certain species exist (or inhabit) and the edges represent migration paths or movement between the regions. This information is important when looking at breeding patterns or tracking the spread of disease, parasites or how changes to the movement can affect other species.

Graphs are also commonly used in molecular biology and genomics to model and analyse datasets with complex relationships. For example, graph-based methods are often used to 'cluster' cells together into cell-types in single-cell transcriptome analysis. Another use is to model genes or proteins in a pathway and study the relationships between them, such as metabolic pathways and gene regulatory networks . Evolutionary trees, ecological networks, and hierarchical clustering of gene expression patterns are also represented as graph structures. Graph-based methods are pervasive that researchers in some fields of biology and these will only become far more widespread as technology develops to leverage this kind of high-throughout multidimensional data.

Graph theory is also used in connectomics; nervous systems can be seen as a graph, where the nodes are neurons and the edges are the connections between them.

Mathematics

In mathematics, graphs are useful in geometry and certain parts of topology such as knot theory. Algebraic graph theory has close links with group theory. Algebraic graph theory has been applied to many areas including dynamic systems and complexity.

Other topics

A graph structure can be extended by assigning a weight to each edge of the graph. Graphs with weights, or weighted graphs, are used to represent structures in which pairwise connections have some numerical values. For example, if a graph represents a road network, the weights could represent the length of each road. There may be several weights associated with each edge, including distance (as in the previous example), travel time, or monetary cost. Such weighted graphs are commonly used to program GPS's, and travel-planning search engines that compare flight times and costs.

History

The Königsberg Bridge problem

The paper written by Leonhard Euler on the Seven Bridges of Königsberg and published in 1736 is regarded as the first paper in the history of graph theory. This paper, as well as the one written by Vandermonde on the knight problem, carried on with the analysis situs initiated by Leibniz. Euler's formula relating the number of edges, vertices, and faces of a convex polyhedron was studied and generalized by Cauchy and L'Huilier, and represents the beginning of the branch of mathematics known as topology.

More than one century after Euler's paper on the bridges of Königsberg and while Listing was introducing the concept of topology, Cayley was led by an interest in particular analytical forms arising from differential calculus to study a particular class of graphs, the trees. This study had many implications for theoretical chemistry. The techniques he used mainly concern the enumeration of graphs with particular properties. Enumerative graph theory then arose from the results of Cayley and the fundamental results published by Pólya between 1935 and 1937. These were generalized by De Bruijn in 1959. Cayley linked his results on trees with contemporary studies of chemical composition. The fusion of ideas from mathematics with those from chemistry began what has become part of the standard terminology of graph theory.

In particular, the term "graph" was introduced by Sylvester in a paper published in 1878 in Nature, where he draws an analogy between "quantic invariants" and "co-variants" of algebra and molecular diagrams:

"[…] Every invariant and co-variant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph. […] I give a rule for the geometrical multiplication of graphs, i.e. for constructing a graph to the product of in- or co-variants whose separate graphs are given. […]" (italics as in the original).

The first textbook on graph theory was written by Dénes Kőnig, and published in 1936. Another book by Frank Harary, published in 1969, was "considered the world over to be the definitive textbook on the subject", and enabled mathematicians, chemists, electrical engineers and social scientists to talk to each other. Harary donated all of the royalties to fund the Pólya Prize.

One of the most famous and stimulating problems in graph theory is the four color problem: "Is it true that any map drawn in the plane may have its regions colored with four colors, in such a way that any two regions having a common border have different colors?" This problem was first posed by Francis Guthrie in 1852 and its first written record is in a letter of De Morgan addressed to Hamilton the same year. Many incorrect proofs have been proposed, including those by Cayley, Kempe, and others. The study and the generalization of this problem by Tait, Heawood, Ramsey and Hadwiger led to the study of the colorings of the graphs embedded on surfaces with arbitrary genus. Tait's reformulation generated a new class of problems, the factorization problems, particularly studied by Petersen and Kőnig. The works of Ramsey on colorations and more specially the results obtained by Turán in 1941 was at the origin of another branch of graph theory, extremal graph theory.

The four color problem remained unsolved for more than a century. In 1969 Heinrich Heesch published a method for solving the problem using computers. A computer-aided proof produced in 1976 by Kenneth Appel and Wolfgang Haken makes fundamental use of the notion of "discharging" developed by Heesch. The proof involved checking the properties of 1,936 configurations by computer, and was not fully accepted at the time due to its complexity. A simpler proof considering only 633 configurations was given twenty years later by Robertson, Seymour, Sanders and Thomas.

The autonomous development of topology from 1860 and 1930 fertilized graph theory back through the works of Jordan, Kuratowski and Whitney. Another important factor of common development of graph theory and topology came from the use of the techniques of modern algebra. The first example of such a use comes from the work of the physicist Gustav Kirchhoff, who published in 1845 his Kirchhoff's circuit laws for calculating the voltage and current in electric circuits. 

The introduction of probabilistic methods in graph theory, especially in the study of Erdős and Rényi of the asymptotic probability of graph connectivity, gave rise to yet another branch, known as random graph theory, which has been a fruitful source of graph-theoretic results.

Graph drawing

Graphs are represented visually by drawing a point or circle for every vertex, and drawing a line between two vertices if they are connected by an edge. If the graph is directed, the direction is indicated by drawing an arrow. 

A graph drawing should not be confused with the graph itself (the abstract, non-visual structure) as there are several ways to structure the graph drawing. All that matters is which vertices are connected to which others by how many edges and not the exact layout. In practice, it is often difficult to decide if two drawings represent the same graph. Depending on the problem domain some layouts may be better suited and easier to understand than others. 

The pioneering work of W. T. Tutte was very influential on the subject of graph drawing. Among other achievements, he introduced the use of linear algebraic methods to obtain graph drawings.

Graph drawing also can be said to encompass problems that deal with the crossing number and its various generalizations. The crossing number of a graph is the minimum number of intersections between edges that a drawing of the graph in the plane must contain. For a planar graph, the crossing number is zero by definition.

Drawings on surfaces other than the plane are also studied.

Graph-theoretic data structures

There are different ways to store graphs in a computer system. The data structure used depends on both the graph structure and the algorithm used for manipulating the graph. Theoretically one can distinguish between list and matrix structures but in concrete applications the best structure is often a combination of both. List structures are often preferred for sparse graphs as they have smaller memory requirements. Matrix structures on the other hand provide faster access for some applications but can consume huge amounts of memory. Implementations of sparse matrix structures that are efficient on modern parallel computer architectures are an object of current investigation.

List structures include the incidence list, an array of pairs of vertices, and the adjacency list, which separately lists the neighbors of each vertex: Much like the incidence list, each vertex has a list of which vertices it is adjacent to.

Matrix structures include the incidence matrix, a matrix of 0's and 1's whose rows represent vertices and whose columns represent edges, and the adjacency matrix, in which both the rows and columns are indexed by vertices. In both cases a 1 indicates two adjacent objects and a 0 indicates two non-adjacent objects. The degree matrix indicates the degree of vertices. The Laplacian matrix is a modified form of the adjacency matrix that incorporates information about the degrees of the vertices, and is useful in some calculations such as Kirchhoff's theorem on the number of spanning trees of a graph. The distance matrix, like the adjacency matrix, has both its rows and columns indexed by vertices, but rather than containing a 0 or a 1 in each cell it contains the length of a shortest path between two vertices.

Problems

Enumeration

There is a large literature on graphical enumeration: the problem of counting graphs meeting specified conditions. Some of this work is found in Harary and Palmer (1973).

Subgraphs, induced subgraphs, and minors

A common problem, called the subgraph isomorphism problem, is finding a fixed graph as a subgraph in a given graph. One reason to be interested in such a question is that many graph properties are hereditary for subgraphs, which means that a graph has the property if and only if all subgraphs have it too. Unfortunately, finding maximal subgraphs of a certain kind is often an NP-complete problem. For example:

• Finding the largest complete subgraph is called the clique problem (NP-complete).

One special case of subgraph isomorphism is the graph isomorphism problem. It asks whether two graphs are isomorphic. It is not known whether this problem is NP-complete, nor whether it can be solved in polynomial time. 

A similar problem is finding induced subgraphs in a given graph. Again, some important graph properties are hereditary with respect to induced subgraphs, which means that a graph has a property if and only if all induced subgraphs also have it. Finding maximal induced subgraphs of a certain kind is also often NP-complete. For example:

• Finding the largest edgeless induced subgraph or independent set is called the independent set problem (NP-complete).

Still another such problem, the minor containment problem, is to find a fixed graph as a minor of a given graph. A minor or subcontraction of a graph is any graph obtained by taking a subgraph and contracting some (or no) edges. Many graph properties are hereditary for minors, which means that a graph has a property if and only if all minors have it too. For example, Wagner's Theorem states:

• A graph is planar if it contains as a minor neither the complete bipartite graph K_3,3 (see the Three-cottage problem) nor the complete graph K₅.

A similar problem, the subdivision containment problem, is to find a fixed graph as a subdivision of a given graph. A subdivision or homeomorphism of a graph is any graph obtained by subdividing some (or no) edges. Subdivision containment is related to graph properties such as planarity. For example, Kuratowski's Theorem states:

• A graph is planar if it contains as a subdivision neither the complete bipartite graph K_3,3 nor the complete graph K₅.

Another problem in subdivision containment is the Kelmans–Seymour conjecture:

• Every 5-vertex-connected graph that is not planar contains a subdivision of the 5-vertex complete graph K₅.

Another class of problems has to do with the extent to which various species and generalizations of graphs are determined by their point-deleted subgraphs. For example:

• The reconstruction conjecture

Graph coloring

Many problems and theorems in graph theory have to do with various ways of coloring graphs. Typically, one is interested in coloring a graph so that no two adjacent vertices have the same color, or with other similar restrictions. One may also consider coloring edges (possibly so that no two coincident edges are the same color), or other variations. Among the famous results and conjectures concerning graph coloring are the following:

• Four-color theorem
• Strong perfect graph theorem
• Erdős–Faber–Lovász conjecture (unsolved)
• Total coloring conjecture, also called Behzad's conjecture (unsolved)
• List coloring conjecture (unsolved)
• Hadwiger conjecture (graph theory) (unsolved)

Subsumption and unification

Constraint modeling theories concern families of directed graphs related by a partial order. In these applications, graphs are ordered by specificity, meaning that more constrained graphs—which are more specific and thus contain a greater amount of information—are subsumed by those that are more general. Operations between graphs include evaluating the direction of a subsumption relationship between two graphs, if any, and computing graph unification. The unification of two argument graphs is defined as the most general graph (or the computation thereof) that is consistent with (i.e. contains all of the information in) the inputs, if such a graph exists; efficient unification algorithms are known. 

For constraint frameworks which are strictly compositional, graph unification is the sufficient satisfiability and combination function. Well-known applications include automatic theorem proving and modeling the elaboration of linguistic structure.

Route problems

• Hamiltonian path problem
• Minimum spanning tree
• Route inspection problem (also called the "Chinese postman problem")
• Seven bridges of Königsberg
• Shortest path problem
• Steiner tree
• Three-cottage problem
• Traveling salesman problem (NP-hard)

Network flow

There are numerous problems arising especially from applications that have to do with various notions of flows in networks, for example:

• Max flow min cut theorem

Visibility problems

• Museum guard problem

Covering problems

Covering problems in graphs may refer to various set cover problems on subsets of vertices/subgraphs.

• Dominating set problem is the special case of set cover problem where sets are the closed neighborhoods.
• Vertex cover problem is the special case of Set cover problem where sets to cover are every edges.
• The original set cover problem, also called hitting set, can be described as a vertex cover in a hypergraph.

Decomposition problems

Decomposition, defined as partitioning the edge set of a graph (with as many vertices as necessary accompanying the edges of each part of the partition), has a wide variety of question. Often, it is required to decompose a graph into subgraphs isomorphic to a fixed graph; for instance, decomposing a complete graph into Hamiltonian cycles. Other problems specify a family of graphs into which a given graph should be decomposed, for instance, a family of cycles, or decomposing a complete graph K_n into n − 1 specified trees having, respectively, 1, 2, 3, ..., n − 1 edges.

Some specific decomposition problems that have been studied include:

• Arboricity, a decomposition into as few forests as possible
• Cycle double cover, a decomposition into a collection of cycles covering each edge exactly twice
• Edge coloring, a decomposition into as few matchings as possible
• Graph factorization, a decomposition of a regular graph into regular subgraphs of given degrees

Graph classes

Many problems involve characterizing the members of various classes of graphs. Some examples of such questions are below:

• Enumerating the members of a class
• Characterizing a class in terms of forbidden substructures
• Ascertaining relationships among classes (e.g. does one property of graphs imply another)
• Finding efficient algorithms to decide membership in a class
• Finding representations for members of a class