Gravity assist

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Gravity_assist 

Animation of Voyager 1's trajectory from 5 September 1977 to 30 December 1981
  Voyager 1 ·   Earth ·   Jupiter ·   Saturn ·   Sun

 

Animation of Voyager 2's trajectory from 20 August 1977 to 30 December 2000
  Voyager 2 ·   Earth ·   Jupiter ·   Saturn ·   Uranus ·   Neptune ·   Sun

In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist maneuver, or swing-by is the use of the relative movement (e.g. orbit around the Sun) and gravity of a planet or other astronomical object to alter the path and speed of a spacecraft, typically to save propellant and reduce expense.

Gravity assistance can be used to accelerate a spacecraft, that is, to increase or decrease its speed or redirect its path. The "assist" is provided by the motion of the gravitating body as it pulls on the spacecraft. The gravity assist maneuver was first used in 1959 when the Soviet probe Luna 3 photographed the far side of Earth's Moon and it was used by interplanetary probes from Mariner 10 onwards, including the two Voyager probes' notable flybys of Jupiter and Saturn.

Explanation

Example encounter.

In the planet's frame of reference, the space probe leaves with the exact same speed at which it had arrived. But when observed in the reference frame of the Solar System (fixed to the Sun), the benefit of this maneuver becomes apparent. Here it can be seen how the probe gains speed by tapping energy from the speed of the planet as it orbits the Sun. (If the trajectory is designed to pass in front of the planet instead of behind it, the gravity assist can be used as a braking maneuver rather than accelerating.) Because the mass of the probe is many orders of magnitude smaller than that of the planet, while the result on the probe is quite significant, the deceleration reaction experienced by the planet, according to Newton's third law, is utterly imperceptible.

 

Possible outcomes of a gravity assist maneuver depending on the velocity vector and flyby position of the incoming spacecraft

A gravity assist around a planet changes a spacecraft's velocity (relative to the Sun) by entering and leaving the gravitational sphere of influence of a planet. The spacecraft's speed increases as it approaches the planet and decreases while escaping its gravitational pull (which is approximately the same), but because the planet orbits the Sun, the spacecraft is affected by this motion during the maneuver. To increase speed, the spacecraft flies with the movement of the planet, acquiring some of the planet's orbital energy in the process; to decrease speed, the spacecraft flies against the movement of the planet to transfer some of its own orbital energy to the planet - in both types of maneuver the energy transfer compared to the planet's total orbital energy is negligible. The sum of the kinetic energies of both bodies remains constant. A slingshot maneuver can therefore be used to change the spaceship's trajectory and speed relative to the Sun.

A close terrestrial analogy is provided by a tennis ball bouncing off the front of a moving train. Imagine standing on a train platform, and throwing a ball at 30 km/h toward a train approaching at 50 km/h. The driver of the train sees the ball approaching at 80 km/h and then departing at 80 km/h after the ball bounces elastically off the front of the train. Because of the train's motion, however, that departure is at 130 km/h relative to the train platform; the ball has added twice the train's velocity to its own.

Translating this analogy into space: in the planet reference frame, the spaceship has a vertical velocity of v relative to the planet. After the slingshot occurs the spaceship is leaving on a course 90 degrees to that which it arrived on. It will still have a velocity of v, but in the horizontal direction. In the Sun reference frame, the planet has a horizontal velocity of v, and by using the Pythagorean Theorem, the spaceship initially has a total velocity of √2v. After the spaceship leaves the planet, it will have a velocity of v + v = 2v, gaining around 0.6v.

This oversimplified example is impossible to refine without additional details regarding the orbit, but if the spaceship travels in a path which forms a hyperbola, it can leave the planet in the opposite direction without firing its engine. This example is also one of many trajectories and gains of speed the spaceship can have.

This explanation might seem to violate the conservation of energy and momentum, apparently adding velocity to the spacecraft out of nothing, but the spacecraft's effects on the planet must also be taken into consideration to provide a complete picture of the mechanics involved. The linear momentum gained by the spaceship is equal in magnitude to that lost by the planet, so the spacecraft gains velocity and the planet loses velocity. However, the planet's enormous mass compared to the spacecraft makes the resulting change in its speed negligibly small even when compared to the orbital perturbations planets undergo due to interactions with other celestial bodies on astronomically short timescales. For example, one metric ton is a typical mass for an interplanetary space probe whereas Jupiter has a mass of almost 2 x 10²⁴ metric tons. Therefore, a one-ton spacecraft passing Jupiter will theoretically cause the planet to lose approximately 5 x 10⁻²⁵ km/s of orbital velocity for every km/s of velocity relative to the Sun gained by the spacecraft. For all practical purposes, since the effects on the planet are so slight (because planets are so much more massive than spacecraft) they can be ignored in the calculation.

Realistic portrayals of encounters in space require the consideration of three dimensions. The same principles apply, only adding the planet's velocity to that of the spacecraft requires vector addition, as shown below.

Two-dimensional schematic of gravitational slingshot. The arrows show the direction in which the spacecraft is traveling before and after the encounter. The length of the arrows shows the spacecraft's speed.

 

Play media

A view from MESSENGER as it uses Earth as a gravitational slingshot to decelerate to allow insertion into an orbit around Mercury.

Due to the reversibility of orbits, gravitational slingshots can also be used to reduce the speed of a spacecraft. Both Mariner 10 and MESSENGER performed this maneuver to reach Mercury.

If even more speed is needed than available from gravity assist alone, the most economical way to use a rocket burn is to do it near the periapsis (closest approach). A given rocket burn always provides the same change in velocity (Δv), but the change in kinetic energy is proportional to the vehicle's velocity at the time of the burn. So to get the most kinetic energy from the burn, the burn must occur at the vehicle's maximum velocity, at periapsis. Oberth effect describes this technique in more detail.

Derivation

The formulae for the gravitational assist can be derived from the familiar formulae for an elastic collision. Both momentum and kinetic energy are conserved, so for bodies with masses ${\displaystyle m_{1}}$ and ${\displaystyle m_{2}}$, and velocities ${\displaystyle u_{1}}$ and ${\displaystyle u_{2}}$ before collision, and ${\displaystyle v_{1}}$ and ${\displaystyle v_{2}}$ after collision. The momentum before and after the collision is expressed by:

${\displaystyle \,\!m_{1}u_{1}+m_{2}u_{2}\ =\ m_{1}v_{1}+m_{2}v_{2}.}$

The kinetic energy is expressed by:

${\displaystyle {\tfrac {1}{2}}m_{1}u_{1}^{2}+{\tfrac {1}{2}}m_{2}u_{2}^{2}\ =\ {\tfrac {1}{2}}m_{1}v_{1}^{2}+{\tfrac {1}{2}}m_{2}v_{2}^{2}.}$

These equations may be solved to find ${\displaystyle v_{1},v_{2}}$ when ${\displaystyle u_{1},u_{2}}$ are known:

${\displaystyle {\begin{array}{ccc}v_{1}&=&\displaystyle {\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}u_{1}+{\frac {2m_{2}}{m_{1}+m_{2}}}u_{2}\\v_{2}&=&\displaystyle {\frac {2m_{1}}{m_{1}+m_{2}}}u_{1}+{\frac {m_{2}-m_{1}}{m_{1}+m_{2}}}u_{2}\end{array}}}$

In the case of a spacecraft flying past a planet, the mass of the spacecraft (${\displaystyle m_{1}}$) is negligible compared with that of a planet (${\displaystyle m_{2}}$) (${\displaystyle m_{1}\ll m_{2}}$), so this reduces to:

${\displaystyle {\begin{array}{ccc}v_{1}&\approx &-u_{1}+2u_{2}\\v_{2}&\approx &u_{2}\end{array}}}$

Historical origins

In his paper "Тем, кто будет читать, чтобы строить" (To those who will be reading [this paper] in order to build [an interplanetary rocket]), published in 1938 but dated 1918–1919, Yuri Kondratyuk suggested that a spacecraft traveling between two planets could be accelerated at the beginning and end of its trajectory by using the gravity of the two planets' moons. This part of his manuscript considering gravity-assists received no later development and it was not published until the 1960s. In his 1925 paper "Проблема полета при помощи реактивных аппаратов: межпланетные полеты" [Problems of flight by jet propulsion: interplanetary flights], Friedrich Zander showed a deep understanding of physics behind the concept of gravity-assist and its potential for the interplanetary exploration of the solar system. This is even more outstanding when considering that other great astrodynamicists of the time, e.g. Guido von Pirquet and Walter Hohmann, never considered gravity-assists.

The first to calculate an interplanetary journey considering multiple gravity-assists was the Italian engineer Gaetano Crocco.

The gravity assist maneuver was first used in 1959 when the Soviet probe Luna 3 photographed the far side of Earth's Moon. The maneuver relied on research performed under the direction of Mstislav Keldysh at the Steklov Institute of Mathematics by, amongst others, Vsevolod Alexandrovich Egorov.

During the summer of 1964 at the NASA Jet Propulsion Laboratory (JPL), Gary Flandro was assigned the task of studying techniques for exploring the outer planets of the solar system. In this study he discovered the rare alignment of the outer planets (Jupiter, Saturn, Uranus, and Neptune) and conceived the Planetary Grand Tour multi-planet mission utilizing the gravity-assist technique to reduce the mission duration from forty years to less than ten years.

Purpose

Plot of Voyager 2's heliocentric velocity against its distance from the Sun, illustrating the use of gravity assist to accelerate the spacecraft by Jupiter, Saturn and Uranus. To observe Triton, Voyager 2 passed over Neptune's north pole resulting in an acceleration out of the plane of the ecliptic and reduced velocity away from the Sun.

A spacecraft traveling from Earth to an inner planet will increase its relative speed because it is falling toward the Sun, and a spacecraft traveling from Earth to an outer planet will decrease its speed because it is leaving the vicinity of the Sun.

Although the orbital speed of an inner planet is greater than that of the Earth, a spacecraft traveling to an inner planet, even at the minimum speed needed to reach it, is still accelerated by the Sun's gravity to a speed notably greater than the orbital speed of that destination planet. If the spacecraft's purpose is only to fly by the inner planet, then there is typically no need to slow the spacecraft. However, if the spacecraft is to be inserted into orbit about that inner planet, then there must be some way to slow it down.

Similarly, while the orbital speed of an outer planet is less than that of the Earth, a spacecraft leaving the Earth at the minimum speed needed to travel to some outer planet is slowed by the Sun's gravity to a speed far less than the orbital speed of that outer planet. Therefore, there must be some way to accelerate the spacecraft when it reaches that outer planet if it is to enter orbit about it.

Rocket engines can certainly be used to increase and decrease the speed of the spacecraft. However, rocket thrust takes propellant, propellant has mass, and even a small change in velocity (known as Δv, or "delta-v", the delta symbol being used to represent a change and "v" signifying velocity) translates to a far larger requirement for propellant needed to escape Earth's gravity well. This is because not only must the primary-stage engines lift the extra propellant, they must also lift the extra propellant beyond that which is needed to lift that additional propellant. The liftoff mass requirement increases exponentially with an increase in the required delta-v of the spacecraft.

Because additional fuel is needed to lift fuel into space, space missions are designed with a tight propellant "budget", known as the "delta-v budget". The delta-v budget is in effect the total propellant that will be available after leaving the earth, for speeding up, slowing down, stabilization against external buffeting (by particles or other external effects), or direction changes, if it cannot acquire more propellant. The entire mission must be planned within that capability. Therefore, methods of speed and direction change that do not require fuel to be burned are advantageous, because they allow extra maneuvering capability and course enhancement, without spending fuel from the limited amount which has been carried into space. Gravity assist maneuvers can greatly change the speed of a spacecraft without expending propellant, and can save significant amounts of propellant, so they are a very common technique to save fuel.

Limits

The trajectories that enabled NASA's twin Voyager spacecraft to tour the four giant planets and achieve velocity to escape the Solar System

The main practical limit to the use of a gravity assist maneuver is that planets and other large masses are seldom in the right places to enable a voyage to a particular destination. For example, the Voyager missions which started in the late 1970s were made possible by the "Grand Tour" alignment of Jupiter, Saturn, Uranus and Neptune. A similar alignment will not occur again until the middle of the 22nd century. That is an extreme case, but even for less ambitious missions there are years when the planets are scattered in unsuitable parts of their orbits.

Another limitation is the atmosphere, if any, of the available planet. The closer the spacecraft can approach, the faster its periapsis speed as gravity accelerates the spacecraft, allowing for more kinetic energy to be gained from a rocket burn. However, if a spacecraft gets too deep into the atmosphere, the energy lost to drag can exceed that gained from the planet's gravity. On the other hand, the atmosphere can be used to accomplish aerobraking. There have also been theoretical proposals to use aerodynamic lift as the spacecraft flies through the atmosphere. This maneuver, called an aerogravity assist, could bend the trajectory through a larger angle than gravity alone, and hence increase the gain in energy.

Even in the case of an airless body, there is a limit to how close a spacecraft may approach. The magnitude of the achievable change in velocity depends on the spacecraft's approach velocity and the planet's escape velocity at the point of closest approach (limited by either the surface or the atmosphere.)

Interplanetary slingshots using the Sun itself are not possible because the Sun is at rest relative to the Solar System as a whole. However, thrusting when near the Sun has the same effect as the powered slingshot described as the Oberth effect. This has the potential to magnify a spacecraft's thrusting power enormously, but is limited by the spacecraft's ability to resist the heat.

An interstellar slingshot using the Sun is conceivable, involving for example an object coming from elsewhere in our galaxy and swinging past the Sun to boost its galactic travel. The energy and angular momentum would then come from the Sun's orbit around the Milky Way. This concept features prominently in Arthur C. Clarke's 1972 award-winning novel Rendezvous With Rama; his story concerns an interstellar spacecraft that uses the Sun to perform this sort of maneuver, and in the process alarms many nervous humans.

A rotating black hole might provide additional assistance, if its spin axis is aligned the right way. General relativity predicts that a large spinning mass produces frame-dragging—close to the object, space itself is dragged around in the direction of the spin. Any ordinary rotating object produces this effect. Although attempts to measure frame dragging about the Sun have produced no clear evidence, experiments performed by Gravity Probe B have detected frame-dragging effects caused by Earth. General relativity predicts that a spinning black hole is surrounded by a region of space, called the ergosphere, within which standing still (with respect to the black hole's spin) is impossible, because space itself is dragged at the speed of light in the same direction as the black hole's spin. The Penrose process may offer a way to gain energy from the ergosphere, although it would require the spaceship to dump some "ballast" into the black hole, and the spaceship would have had to expend energy to carry the "ballast" to the black hole.

Tisserand parameter and gravity assists

The use of gravity assists is constrained by a conserved quantity called the Tisserand parameter (or invariant). This is an approximation to the Jacobi constant of the restricted three-body problem. Considering the case a comet orbiting the Sun and the effects a Jupiter encounter would have, Félix Tisserand showed that

${\displaystyle T_{P}\ ={\frac {a_{J}}{a}}+2\cdot {\sqrt {{\frac {a}{a_{J}}}(1-e^{2})}}\cos i}$

will remain constant (where ${\displaystyle a\,\!}$ is the comet's semi-major axis, ${\displaystyle e\,\!}$ its eccentricity, ${\displaystyle i\,\!}$ its inclination, and ${\displaystyle a_{J}}$ is the semi-major axis of Jupiter). This applies when the comet is sufficiently far from Jupiter to have well-defined orbital elements and to the extent that Jupiter is much less massive than the Sun and on a circular orbit.

This quantity is conserved for any system of three objects, one of which has negligible mass, and another of which is of intermediate mass and on a circular orbit. Examples are the Sun, Earth and a spacecraft, or Saturn, Titan and the Cassini spacecraft (using the semi-major axis of the perturbing body instead of ${\displaystyle a_{J}}$). This imposes a constraint on how a gravity assist may be used to alter a spacecraft's orbit.

The Tisserand parameter will change if the spacecraft makes a propulsive maneuver or a gravity assist of some fourth object, which is one reason that many spacecraft frequently combine Earth and Venus (or Mars) gravity assists or also perform large deep space maneuvers.

Timeline of notable examples

Luna 3

The gravity assist maneuver was first used in 1959 when Luna 3 photographed the far side of Earth's Moon.

Pioneer program

Gary Flandro's mission architecture would ultimately be accomplished in the late 1970s by the two Voyager probes, but in order to prepare for it, NASA decided in 1964 to experiment with launching a pair of probes to the outer Solar System. An advocacy group named the Outer Space Panel and chaired by American space scientist James A. Van Allen, worked out the scientific rationale for exploring the outer planets. NASA Goddard Spaceflight Center put together a proposal for a pair of "Galactic Jupiter Probes" that would pass through the asteroid belt and visit Jupiter. These were to be launched in 1972 and 1973 during favorable windows that occurred only a few weeks every 13 months. Launch during other time intervals would have been more costly in terms of propellant requirements.

Approved by NASA in February 1969, the twin spacecraft were designated Pioneer F and Pioneer G before launch; later they were named Pioneer 10 and Pioneer 11. They formed part of the Pioneer program, a series of United States unmanned space missions launched between 1958 and 1978. This model was the first in the series to be designed for exploring the outer Solar System. Based on multiple proposals issued throughout the 1960s, the early mission objectives were to explore the interplanetary medium past the orbit of Mars, study the asteroid belt and assess the possible hazard to spacecraft traveling through the belt, and explore Jupiter and its environment. Later development-stage objectives included the probe closely approaching Jupiter to provide data on the effect the environmental radiation surrounding Jupiter would have on the spacecraft instruments.

Pioneer 10

Pioneer 10 (originally designated Pioneer F) is an American space probe, launched in 1972 and weighing 258 kilograms (569 pounds), that completed the first mission to the planet Jupiter. Thereafter, Pioneer 10 became the first of five artificial objects to achieve the escape velocity needed to leave the Solar System. This space exploration project was conducted by the NASA Ames Research Center in California, and the space probe was manufactured by TRW Inc.

It was launched on March 2, 1972, by an Atlas-Centaur expendable vehicle from Cape Canaveral, Florida. Between July 15, 1972, and February 15, 1973, it became the first spacecraft to traverse the asteroid belt. Photography of Jupiter began November 6, 1973, at a range of 25,000,000 kilometers (16,000,000 mi), and about 500 images were transmitted. The closest approach to the planet was on December 4, 1973 (02:26 UT), at a range of 130,354 kilometers (80,998 mi). During the mission, the on-board instruments were used to study the asteroid belt, the environment around Jupiter, the solar wind, cosmic rays, and eventually the far reaches of the Solar System and heliosphere.

Radio communications were lost with Pioneer 10 on January 23, 2003, because of the loss of electric power for its radio transmitter, with the probe at a distance of 12 billion kilometers (80 AU) from Earth.

In December 1973, Pioneer 10 spacecraft was the first one to use the gravitational slingshot effect to reach escape velocity to leave Solar System.

Pioneer 11

Pioneer 11 (also known as Pioneer G) is a 260-kilogram (570 lb) robotic space probe launched by NASA on April 6, 1973 to study the asteroid belt, the environment around Jupiter and Saturn, solar winds, and cosmic rays. It was the first probe to encounter Saturn, the second to fly through the asteroid belt, and the second to fly by Jupiter. Later, Pioneer 11 became the second of five artificial objects to achieve an escape velocity allowing it to leave the Solar System. Due to power constraints and the vast distance to the probe, the last routine contact with the spacecraft was on September 30, 1995, and the last good engineering data was received on November 24, 1995.

Mariner 10

The Mariner 10 probe was the first spacecraft to use the gravitational slingshot effect to reach another planet, passing by Venus on 5 February 1974 on its way to becoming the first spacecraft to explore Mercury.

Voyager

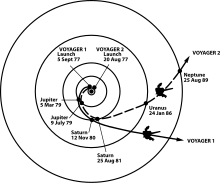
Gary Flandro's work was exploited by NASA with the Voyager 1 and Voyager 2 missions, launched in 1977.

Voyager 1

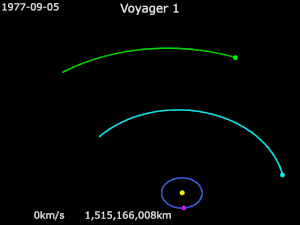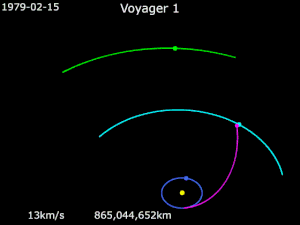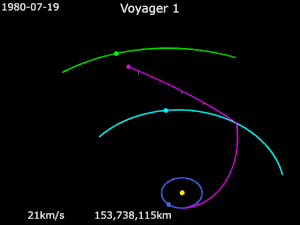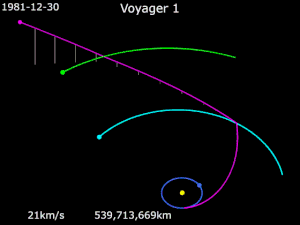
Voyager 1 is a space probe that was launched by NASA on September 5, 1977. Part of the Voyager program to study the outer Solar System, Voyager 1 was launched 16 days after its twin, Voyager 2. It gained the energy to escape the Sun's gravity completely by performing slingshot maneuvers around Jupiter and Saturn. Having operated for 43 years, 10 months and 30 days as of August 5, 2021 UTC, the spacecraft still communicates with the Deep Space Network to receive routine commands and to transmit data to Earth. Real-time distance and velocity data is provided by NASA and JPL. At a distance of 152.2 AU (22.8 billion km; 14.1 billion mi) from Earth as of January 12, 2020, it is the most distant human-made object from Earth.

The probe's objectives included flybys of Jupiter, Saturn, and Saturn's largest moon, Titan. Although the spacecraft's course could have been altered to include a Pluto encounter by forgoing the Titan flyby, exploration of the moon took priority because it was known to have a substantial atmosphere. Voyager 1 studied the weather, magnetic fields, and rings of the two planets, and was the first probe to provide detailed images of their moons.

As part of the Voyager program, like its sister craft Voyager 2, the spacecraft is in an extended mission to locate and study the regions and boundaries of the outer heliosphere, and to begin exploring the interstellar medium. Voyager 1 crossed the heliopause and entered interstellar space on August 25, 2012, making it the first spacecraft to do so. Two years later, Voyager 1 began experiencing a third "tsunami wave" of coronal mass ejections from the Sun, that has continued to at least December 15, 2014, further confirming that the probe is indeed in interstellar space.

In a further testament to the robustness of Voyager 1, the Voyager team tested the spacecraft's trajectory correction maneuver (TCM) thrusters in late 2017 (the first time these thrusters had been fired since 1980), a project enabling the mission to be extended by two to three years. Voyager 1's extended mission is expected to continue until about 2025, when its radioisotope thermoelectric generators (RTGs) will no longer supply enough electric power to operate its scientific instruments.

Voyager 2

Voyager 2 is a space probe launched by NASA on August 20, 1977, to study the outer planets. A part of the Voyager program, it was launched 16 days before its twin, Voyager 1, on a trajectory that took longer to reach Jupiter and Saturn but enabled further encounters with Uranus and Neptune. It is the only spacecraft to have visited either of these two ice giant planets. Voyager 2 was the fourth of five spacecraft to achieve the Solar escape velocity, which allowed it to leave the Solar System.

Its primary mission ended with the exploration of the Neptunian system on October 2, 1989, after having visited the Jovian system in 1979, the Saturnian system in 1981, and the Uranian system in 1986. Voyager 2 is now in its extended mission to study Interstellar Space and has been operating for 43 years, 11 months and 15 days as of August 5, 2021. It remains in contact through the NASA Deep Space Network. Maintenance to the Deep Space Network created the longest period of silence in outbound communications to the probe for a period of 8 months. Contact was reestablished on November 2, 2020, when a series of instructions was transmitted, subsequently executed and relayed back with a successful communication message. As of February 12, 2021, full communications with the probe was restored after a major antenna upgrade that took a year to complete. The DSS 43 communication antenna, solely responsible for communications with the probe, is located in Canberra, Australia.

On November 5, 2018, at a distance of 122 AU (1.83×10¹⁰ km) (about 16:58 light-hours) from the Sun, moving at a velocity of 15.341 km/s (55,230 km/h) relative to the Sun, Voyager 2 left the heliosphere, and entered the interstellar medium (ISM), a region of outer space beyond the influence of the Solar System, joining Voyager 1 which had reached the interstellar medium in 2012. Voyager 2 has begun to provide the first direct measurements of the density and temperature of the interstellar plasma.

Galileo

Animation of Galileo's trajectory from 19 October 1989 to 30 September 2003
  Galileo ·   Jupiter ·   Earth ·    Venus ·   951 Gaspra ·   243 Ida

The Galileo spacecraft was launched by NASA in 1989 aboard Space Shuttle Atlantis. Its original mission was designed to use a direct Hohmann transfer. However, Galileo's intended booster, the cryogenically fueled Centaur booster rocket was prohibited as a Shuttle "cargo" for safety considerations following the loss of Space Shuttle Challenger. With its substituted solid rocket upper stage, the IUS, which could not provide as much delta-v, Galileo did not ascend directly to Jupiter, but flew by Venus once and Earth twice in order to reach Jupiter in December 1995.

The Galileo engineering review speculated (but was never able to prove conclusively) that this longer flight time coupled with the stronger sunlight near Venus caused lubricant in Galileo's main antenna to fail, forcing the use of a much smaller backup antenna with a consequent lowering of data rate from the spacecraft.

Its subsequent tour of the Jovian moons also used numerous slingshot maneuvers with those moons to conserve fuel and maximize the number of encounters.

Ulysses

Animation of Ulysses' trajectory from 6 October 1990 to 29 June 2009
  Ulysses ·   Earth ·   Jupiter ·   C/2006 P1 ·   C/1996 B2 ·   C/1999 T1

In 1990, NASA launched the ESA spacecraft Ulysses to study the polar regions of the Sun. All the planets orbit approximately in a plane aligned with the equator of the Sun. Thus, to enter an orbit passing over the poles of the Sun, the spacecraft would have to eliminate the 30 km/s speed it inherited from the Earth's orbit around the Sun and gain the speed needed to orbit the Sun in the pole-to-pole plane, tasks that are impossible with current spacecraft propulsion systems alone, making gravity assist maneuvers essential.

Accordingly, Ulysses was first sent toward Jupiter and aimed to arrive at a point in space just ahead and south of the planet. As it passed Jupiter, the probe fell through the planet's gravity field, exchanging momentum with the planet. The gravity assist maneuver bent the probe's trajectory northward relative to the Ecliptic Plane onto an orbit which passes over the poles of the Sun. By using this maneuver, Ulysses needed only enough propellant to send it to a point near Jupiter, which is well within current capability.

MESSENGER

Animation of MESSENGER's trajectory from 3 August 2004 to 31 March 2011
  MESSENGER ·   Earth ·   Mercury ·   Venus

The MESSENGER mission (launched in August 2004) made extensive use of gravity assists to slow its speed before orbiting Mercury. The MESSENGER mission included one flyby of Earth, two flybys of Venus, and three flybys of Mercury before finally arriving at Mercury in March 2011 with a velocity low enough to permit orbit insertion with available fuel. Although the flybys were primarily orbital maneuvers, each provided an opportunity for significant scientific observations.

Cassini

The Cassini–Huygens spacecraft passed by Venus twice, then Earth, and finally Jupiter on the way to Saturn. The 6.7-year transit was slightly longer than the six years needed for a Hohmann transfer, but cut the extra velocity (delta-v) needed to about 2 km/s, so that the large and heavy Cassini probe was able to reach Saturn, which would not have been possible in a direct transfer even with the Titan IV, the largest launch vehicle available at the time. A Hohmann transfer to Saturn would require a total of 15.7 km/s delta-v (disregarding Earth's and Saturn's own gravity wells, and disregarding aerobraking), which is not within the capabilities of current launch vehicles and spacecraft propulsion systems.

Cassini interplanetary trajectory

 

Animation of Cassini's trajectory from 15 October 1997 to 4 May 2008
  Cassini–Huygens ·   Jupiter ·   Saturn ·   Earth ·   Venus ·    2685 Masursky

Cassini's speed relative to the Sun. Gravity assists form peaks to the left, while periodic variations on the right are caused by the spacecraft's orbit around Saturn.

After entering orbit around Saturn, the Cassini spacecraft used multiple Titan gravity assists to navigate through a complex orbital tour. A typical Titan encounter changed the spacecraft's velocity by 0.75 km/s, and the spacecraft made 127 Titan encounters. These encounters enabled an orbital tour with a wide range of periapsis and apoapsis distances, various alignments of the orbit with respect to the Sun, and orbital inclinations from 0° to 74°.

Rosetta

Animation of Rosetta's trajectory from 2 March 2004 to 9 September 2016
  Rosetta ·   67P/C-G ·   Earth ·   Mars ·   21 Lutetia  ·   2867 Šteins

The Rosetta probe, launched in March 2004, used four gravity assist maneuvers (including one just 250 km from the surface of Mars) to accelerate throughout the inner Solar System. That enabled it to match the velocity of the 67P/Churyumov–Gerasimenko comet at the rendezvous point in August 2014.

Juno

The Juno spacecraft was launched on August 5, 2011 (UTC). The trajectory used a gravity assist speed boost from Earth, accomplished by an Earth flyby in October 2013, two years after its launch on August 5, 2011. In that way Juno changed its orbit (and speed) toward its final goal, Jupiter, after only five years.

Animation of Juno's trajectory from August 5, 2011, to July 30, 2021
  Juno ·   Earth ·   Mars ·   Jupiter

Parker Solar Probe

NASA's Parker Solar Probe mission, launched in 2018, will use multiple gravity assists at Venus to remove the Earth's angular momentum from the orbit to drop to a distance of 8.5 solar radii (5.9 Gm) from the Sun. Parker Solar Probe's mission will be the closest approach to the Sun by any space mission.

BepiColombo

Animation of BepiColombo's trajectory from 20 October 2018 to 2 November 2025
   BepiColombo ·   Earth ·   Venus ·   Mercury ·   Sun

BepiColombo is a joint mission of the European Space Agency (ESA) and the Japan Aerospace Exploration Agency (JAXA) to the planet Mercury. It was launched in 20 October 2018. It will use the gravity assist technique with Earth once, with Venus twice, and six times with Mercury. BepiColombo is named after Giuseppe (Bepi) Colombo who was a pioneer thinker with this way of maneuvers.

 

Interplanetary Transport Network

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Interplanetary_Transport_Network 

This stylized depiction of the ITN is designed to show its (often convoluted) path through the Solar System. The green ribbon represents one path from among the many that are mathematically possible along the surface of the darker green bounding tube. Locations where the ribbon changes direction abruptly represent trajectory changes at Lagrange points, while constricted areas represent locations where objects linger in temporary orbit around a point before continuing on.

The Interplanetary Transport Network (ITN) is a collection of gravitationally determined pathways through the Solar System that require very little energy for an object to follow. The ITN makes particular use of Lagrange points as locations where trajectories through space can be redirected using little or no energy. These points have the peculiar property of allowing objects to orbit around them, despite lacking an object to orbit. While it would use little energy, transport along the network would take a long time.

History

Interplanetary transfer orbits are solutions to the gravitational three-body problem, which, for the general case, does not have analytical solutions, and is addressed by numerical analysis approximations. However, a small number of exact solutions exist, most notably the five orbits referred to as "Lagrange points", which are orbital solutions for circular orbits in the case when one body is significantly more massive.

The key to discovering the Interplanetary Transport Network was the investigation of the nature of the winding paths near the Earth-Sun and Earth-Moon Lagrange points. They were first investigated by Henri Poincaré in the 1890s. He noticed that the paths leading to and from any of those points would almost always settle, for a time, on an orbit about that point. There are in fact an infinite number of paths taking one to the point and away from it, and all of which require nearly zero change in energy to reach. When plotted, they form a tube with the orbit about the Lagrange point at one end.

The derivation of these paths traces back to mathematicians Charles C. Conley and Richard P. McGehee in 1968. Hiten, Japan's first lunar probe, was moved into lunar orbit using similar insight into the nature of paths between the Earth and the Moon. Beginning in 1997, Martin Lo, Shane D. Ross, and others wrote a series of papers identifying the mathematical basis that applied the technique to the Genesis solar wind sample return, and to lunar and Jovian missions. They referred to it as an Interplanetary Superhighway (IPS).

Paths

As it turns out, it is very easy to transit from a path leading to the point to one leading back out. This makes sense, since the orbit is unstable, which implies one will eventually end up on one of the outbound paths after spending no energy at all. Edward Belbruno coined the term "weak stability boundary" or "fuzzy boundary" for this effect.

With careful calculation, one can pick which outbound path one wants. This turned out to be useful, as many of these paths lead to some interesting points in space, such as the Earth's Moon or between the Galilean moons of Jupiter. As a result, for the cost of reaching the Earth–Sun L₂ point, which is rather low energy value, one can travel to a number of very interesting points for a little or no additional fuel cost. But the trip from Earth to Mars or other distant locations would likely take thousands of years.

The transfers are so low-energy that they make travel to almost any point in the Solar System possible. On the downside, these transfers are very slow. For trips from Earth to other planets, they are not useful for manned or unmanned probes, as the trip would take many generations. Nevertheless, they have already been used to transfer spacecraft to the Earth–Sun L₁ point, a useful point for studying the Sun that was employed in a number of recent missions, including the Genesis mission, the first to return solar wind samples to Earth. The network is also relevant to understanding Solar System dynamics; Comet Shoemaker–Levy 9 followed such a trajectory on its collision path with Jupiter.

Further explanation

The ITN is based around a series of orbital paths predicted by chaos theory and the restricted three-body problem leading to and from the orbits around the Lagrange points – points in space where the gravity between various bodies balances with the centrifugal force of an object there. For any two bodies in which one body orbits around the other, such as a star/planet or planet/moon system, there are five such points, denoted L₁ through L₅. For instance, the Earth–Moon L₁ point lies on a line between the two, where gravitational forces between them exactly balance with the centrifugal force of an object placed in orbit there. These five points have particularly low delta-v requirements, and appear to be the lowest-energy transfers possible, even lower than the common Hohmann transfer orbit that has dominated orbital navigation since the start of space travel.

Although the forces balance at these points, the first three points (the ones on the line between a certain large mass, e.g. a star, and a smaller, orbiting mass, e.g. a planet) are not stable equilibrium points. If a spacecraft placed at the Earth–Moon L₁ point is given even a slight nudge away from the equilibrium point, the spacecraft's trajectory will diverge away from the L₁ point. The entire system is in motion, so the spacecraft will not actually hit the Moon, but will travel in a winding path, off into space. There is, however, a semi-stable orbit around each of these points, called a halo orbit. The orbits for two of the points, L₄ and L₅, are stable, but the halo orbits for L₁ through L₃ are stable only on the order of months.

In addition to orbits around Lagrange points, the rich dynamics that arise from the gravitational pull of more than one mass yield interesting trajectories, also known as low energy transfers. For example, the gravity environment of the Sun–Earth–Moon system allows spacecraft to travel great distances on very little fuel, albeit on an often circuitous route.

Missions

Launched in 1978, the ISEE-3 spacecraft was sent on a mission to orbit around one of the Lagrange points. The spacecraft was able to maneuver around the Earth's neighborhood using little fuel by taking advantage of the unique gravity environment. After the primary mission was completed, ISEE-3 went on to accomplish other goals, including a flight through the geomagnetic tail and a comet flyby. The mission was subsequently renamed the International Cometary Explorer (ICE).

The first low energy transfer using what would later be called the ITN was the rescue of Japan's Hiten lunar mission in 1991.

Another example of the use of the ITN was NASA's 2001–2003 Genesis mission, which orbited the Sun–Earth L₁ point for over two years collecting material, before being redirected to the L₂ Lagrange point, and finally redirected from there back to Earth.

The 2003–2006 SMART-1 of the European Space Agency used another low energy transfer from the ITN.

In a more recent example, the Chinese spacecraft Chang'e 2 used the ITN to travel from lunar orbit to the Earth-Sun L₂ point, then on to fly by the asteroid 4179 Toutatis.

Asteroids

The asteroid 39P/Oterma's path from outside Jupiters orbit, to inside, and back to outside is said to use these low energy paths.