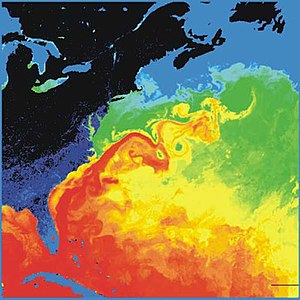
The Gulf Stream, together with its northern extension the North Atlantic Drift, is a warm and swift Atlantic ocean current that originates in the Gulf of Mexico and stretches to the tip of Florida and follows the eastern coastlines of the United States and Newfoundland before crossing the Atlantic Ocean as the North Atlantic Current. The process of western intensification causes the Gulf Stream to be a northwards accelerating current off the east coast of North America. At about 40°0′N 30°0′W, it splits in two, with the northern stream, the North Atlantic Drift, crossing to Northern Europe and the southern stream, the Canary Current, recirculating off West Africa.
The Gulf Stream influences the climate of the east coast of North America from Florida to Newfoundland and the west coast of Europe. Although there has been recent debate, there is consensus that the climate of Western Europe and Northern Europe is warmer than other areas of similar latitude because of the North Atlantic Current. It is part of the North Atlantic Gyre. Its presence has led to the development of strong cyclones of all types, both within the atmosphere and within the ocean. The Gulf Stream is also a significant potential source of renewable power generation.
History
European discovery of the Gulf Stream dates to the 1512 expedition of Juan Ponce de León, after which it became widely used by Spanish ships sailing from the Caribbean to Spain. A summary of Ponce de León's voyage log on April 22, 1513, noted, "A current such that, although they had great wind, they could not proceed forwards, but backwards and it seems that they were proceeding well; at the end, it was known that the current was more powerful than the wind."
Benjamin Franklin became interested in the North Atlantic Ocean circulation patterns. In 1768, while in England, Franklin heard a curious complaint from the Colonial Board of Customs: Why did it take British packets several weeks longer to reach New York from England than it took an average American merchant ship to reach Newport, Rhode Island, despite the merchant ships leaving from London and having to sail down the River Thames and then the length of the English Channel before they sailed across the Atlantic, while the packets left from Falmouth in Cornwall?
Franklin asked Timothy Folger, a Nantucket Island whaling captain, for an answer. Folger explained that merchant ships routinely crossed the current—which was identified by whale behaviour, measurement of the water's temperature, and changes in the water's colour—while the mail packet captains ran against it. Franklin had Folger sketch the path of the current on a chart of the Atlantic and add notes on how to avoid the current when sailing from England to America. Franklin then forwarded the chart to Anthony Todd, secretary of the British Post Office. Franklin's Gulf Stream chart was printed in 1769 in London, but it was mostly ignored by British sea captains. A copy of the chart was printed in Paris circa 1770–1773, and a third version was published by Franklin in Philadelphia in 1786.
Properties
The Gulf Stream proper is a western-intensified current, driven largely by wind stress. The North Atlantic Drift, in contrast, is largely driven by thermohaline circulation. In 1958, oceanographer Henry Stommel noted that "very little water from the Gulf of Mexico is actually in the stream". By carrying warm water northeast across the Atlantic, it makes Western Europe and especially Northern Europe warmer and milder than it otherwise would be.
Formation and behaviour
A river of sea water, called the Atlantic North Equatorial Current, flows westwards off the coast of Central Africa. When this current interacts with the northeastern coast of South America, the current forks into two branches. One passes into the Caribbean Sea, while a second, the Antilles Current, flows north and east of the West Indies. These two branches rejoin north of the Straits of Florida.
The trade winds blow westwards in the tropics, and the westerlies blow eastwards at mid-latitudes. This wind pattern applies a stress to the subtropical ocean surface with negative curl across the north Atlantic Ocean. The resulting Sverdrup transport is equatorward.
Because of the conservation of potential vorticity caused by the northwards-moving winds on the subtropical ridge's western periphery and the increased relative vorticity of northwards moving water, transport is balanced by a narrow, accelerating polewards current. This flows along the western boundary of the ocean basin, outweighing the effects of friction with the western boundary current, and is known as the Labrador Current. The conservation of potential vorticity also causes bends along the Gulf Stream, which occasionally break off as the Gulf Stream's position shifts, forming separate warm and cold eddies. This overall process is known as western intensification, causes currents on the western boundary of an ocean basin, such as the Gulf Stream, to be stronger than those on the eastern boundary.
As a consequence, the resulting Gulf Stream is a strong ocean current. It transports water at a rate of 30 million cubic metres per second (30 sverdrups) through the Florida Straits. As it passes south of Newfoundland, this rate increases to 150 sverdrups. The volume of the Gulf Stream dwarfs all rivers that empty into the Atlantic combined, which total 0.6 sverdrups. It is weaker, however, than the Antarctic Circumpolar Current. Given the strength and proximity of the Gulf Stream, beaches along the East Coast of the United States may be more vulnerable to large sea-level anomalies, which significantly impact rates of coastal erosion.
The Gulf Stream is typically 100 kilometres (62 mi) wide and 800 metres (2,600 ft) to 1,200 metres (3,900 ft) deep. The current velocity is fastest near the surface, with the maximum speed typically about 2.5 metres per second (5.6 mph). As it travels north, the warm water transported by the Gulf Stream undergoes evaporative cooling. The cooling is wind-driven: wind moving over the water causes evaporation, cooling the water and increasing its salinity and density. When sea ice forms, salts are left out of the ice, a process known as brine exclusion. These two processes produce water that is denser and colder (or more precisely, water that is still liquid at a lower temperature). In the North Atlantic Ocean, the water becomes so dense that it begins to sink down through less salty and less dense water. (The convective action is similar to a lava lamp.) This downdraft of cold, dense water becomes a part of the North Atlantic Deep Water, a southgoing stream. Very little seaweed lies within the current, although seaweed lies in clusters to its east.
In April 2018, two studies published in Nature found the Gulf Stream to be at its weakest for at least 1,600 years.
Localized effects
The Gulf Stream is influential on the climate of the Florida peninsula. The portion off the Florida coast, referred to as the Florida Current, maintains an average water temperature of at least 24 °C (75 °F) during the winter. East winds moving over this warm water move warm air from over the Gulf Stream inland, helping to keep temperatures milder across the state than elsewhere across the Southeastern United States during the winter. Also, the Gulf Stream's proximity to Nantucket, Massachusetts adds to its biodiversity, because it is the northern limit for southern varieties of plant life, and the southern limit for northern plant species, Nantucket being warmer during winter than the mainland.
The North Atlantic Current of the Gulf Stream, along with similar warm air currents, helps keep Ireland and the western coast of Great Britain a couple of degrees warmer than the east. However, the difference is most dramatic in the western coastal islands of Scotland. A noticeable effect of the Gulf Stream and the strong westerly winds (driven by the warm water of the Gulf Stream) on Europe occurs along the Norwegian coast. Northern parts of Norway lie close to the Arctic zone, most of which is covered with ice and snow in winter. However, almost all of Norway's coast remains free of ice and snow throughout the year. The warming effect provided by the Gulf Stream has allowed fairly large settlements to be developed and maintained on the coast of Northern Norway, including Tromsø, the third largest city north of the Arctic Circle. Weather systems warmed by the Gulf Stream drift into Northern Europe, also warming the climate behind the Scandinavian mountains.
Effect on cyclone formation
The warm water and temperature contrast along the edge of the Gulf Stream often increase the intensity of cyclones, tropical or otherwise. Tropical cyclone generation normally requires water temperatures in excess of 26.5 °C (79.7 °F). Tropical cyclone formation is common over the Gulf Stream, especially in the month of July. Storms travel westwards through the Caribbean and then either move in a northwards direction and curve towards the eastern coast of the United States or stay on a north-westwards track and enter the Gulf of Mexico. Such storms have the potential to create strong winds and extensive damage to the United States' Southeast Coastal Areas. Hurricane Sandy in 2012 was a recent example of a hurricane passing over the Gulf Stream and gaining strength.
Strong extratropical cyclones have been shown to deepen significantly along a shallow frontal zone, forced by the Gulf Stream, during the cold season. Subtropical cyclones also tend to generate near the Gulf Stream. 75 percent of such systems documented between 1951 and 2000 formed near this warm water current, with two annual peaks of activity occurring during the months of May and October. Cyclones within the ocean form under the Gulf Stream, extending as deep as 3,500 metres (11,500 ft) beneath the ocean's surface.
Possible renewable power source
The theoretical maximum energy dissipation from the Gulf Stream by turbines is in the range of 20–60 GW. One suggestion, which could theoretically supply power comparable to several nuclear power plants, would deploy a field of underwater turbines placed 300 metres (980 ft) under the centre of the core of the Gulf Stream. Ocean thermal energy could also be harnessed to produce electricity using the temperature difference between cold deep water and warm surface water.
Gulf Stream Rings
The Gulf Stream periodically forms rings resulting from a meander of the Gulf Stream being closed off from an alternate route distinctive from that meander, creating an independent eddy. Of these eddies, there are two types: cold core rings, which rotate cyclonically, and warm core rings, which rotate anti cyclonically. These rings have the capacity to transport the distinct biological, chemical, and physical properties of their originating waters to the new waters into which they travel.