Matrix multiplication

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Matrix_multiplication 

 

For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The result matrix has the number of rows of the first and the number of columns of the second matrix.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.

Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812, to represent the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra.

Notation

This article will use the following notational conventions: matrices are represented by capital letters in bold, e.g. A; vectors in lowercase bold, e.g. a; and entries of vectors and matrices are italic (they are numbers from a field), e.g. A and a. Index notation is often the clearest way to express definitions, and is used as standard in the literature. The entry in row i, column j of matrix A is indicated by (A)_ij, A_ij or a_ij. In contrast, a single subscript, e.g. A₁, A₂, is used to select a matrix (not a matrix entry) from a collection of matrices.

Definition

If A is an m × n matrix and B is an n × p matrix,

${\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1p}\\b_{21}&b_{22}&\cdots &b_{2p}\\\vdots &\vdots &\ddots &\vdots \\b_{n1}&b_{n2}&\cdots &b_{np}\\\end{pmatrix}}}$

the matrix product C = AB (denoted without multiplication signs or dots) is defined to be the m × p matrix

${\displaystyle \mathbf {C} ={\begin{pmatrix}c_{11}&c_{12}&\cdots &c_{1p}\\c_{21}&c_{22}&\cdots &c_{2p}\\\vdots &\vdots &\ddots &\vdots \\c_{m1}&c_{m2}&\cdots &c_{mp}\\\end{pmatrix}}}$

such that

${\displaystyle c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}=\sum _{k=1}^{n}a_{ik}b_{kj},}$

for i = 1, ..., m and j = 1, ..., p.

That is, the entry ${\displaystyle c_{ij}}$ of the product is obtained by multiplying term-by-term the entries of the ith row of A and the jth column of B, and summing these n products. In other words, ${\displaystyle c_{ij}}$ is the dot product of the ith row of A and the jth column of B.

Therefore, AB can also be written as

${\displaystyle \mathbf {C} ={\begin{pmatrix}a_{11}b_{11}+\cdots +a_{1n}b_{n1}&a_{11}b_{12}+\cdots +a_{1n}b_{n2}&\cdots &a_{11}b_{1p}+\cdots +a_{1n}b_{np}\\a_{21}b_{11}+\cdots +a_{2n}b_{n1}&a_{21}b_{12}+\cdots +a_{2n}b_{n2}&\cdots &a_{21}b_{1p}+\cdots +a_{2n}b_{np}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}b_{11}+\cdots +a_{mn}b_{n1}&a_{m1}b_{12}+\cdots +a_{mn}b_{n2}&\cdots &a_{m1}b_{1p}+\cdots +a_{mn}b_{np}\\\end{pmatrix}}}$

Thus the product AB is defined if and only if the number of columns in A equals the number of rows in B, in this case n.

In most scenarios, the entries are numbers, but they may be any kind of mathematical objects for which an addition and a multiplication are defined, that are associative, and such that the addition is commutative, and the multiplication is distributive with respect to the addition. In particular, the entries may be matrices themselves (see block matrix).

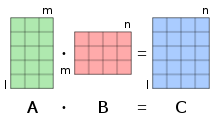
Illustration

The figure to the right illustrates diagrammatically the product of two matrices A and B, showing how each intersection in the product matrix corresponds to a row of A and a column of B.

${\displaystyle {\overset {4\times 2{\text{ matrix}}}{\begin{bmatrix}{a_{11}}&{a_{12}}\\\cdot &\cdot \\{a_{31}}&{a_{32}}\\\cdot &\cdot \\\end{bmatrix}}}{\overset {2\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &{b_{12}}&{b_{13}}\\\cdot &{b_{22}}&{b_{23}}\\\end{bmatrix}}}={\overset {4\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &c_{12}&c_{13}\\\cdot &\cdot &\cdot \\\cdot &c_{32}&c_{33}\\\cdot &\cdot &\cdot \\\end{bmatrix}}}}$

The values at the intersections marked with circles are:

${\displaystyle {\begin{aligned}c_{12}&={a_{11}}{b_{12}}+{a_{12}}{b_{22}}\\c_{33}&={a_{31}}{b_{13}}+{a_{32}}{b_{23}}\end{aligned}}}$

Fundamental applications

Historically, matrix multiplication has been introduced for facilitating and clarifying computations in linear algebra. This strong relationship between matrix multiplication and linear algebra remains fundamental in all mathematics, as well as in physics, chemistry, engineering and computer science.

Linear maps

If a vector space has a finite basis, its vectors are each uniquely represented by a finite sequence of scalars, called a coordinate vector, whose elements are the coordinates of the vector on the basis. These coordinate vectors form another vector space, which is isomorphic to the original vector space. A coordinate vector is commonly organized as a column matrix (also called column vector), which is a matrix with only one column. So, a column vector represents both a coordinate vector, and a vector of the original vector space.

A linear map A from a vector space of dimension n into a vector space of dimension m maps a column vector

${\displaystyle \mathbf {x} ={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}}$

onto the column vector

${\displaystyle \mathbf {y} =A(\mathbf {x} )={\begin{pmatrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}\end{pmatrix}}.}$

The linear map A is thus defined by the matrix

${\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},}$

and maps the column vector ${\displaystyle \mathbf {x} }$ to the matrix product

${\displaystyle \mathbf {y} =\mathbf {Ax} .}$

If B is another linear map from the preceding vector space of dimension m, into a vector space of dimension p, it is represented by a ${\displaystyle p\times m}$ matrix ${\displaystyle \mathbf {B} .}$ A straightforward computation shows that the matrix of the composite map ${\displaystyle B\circ A}$ is the matrix product ${\displaystyle \mathbf {BA} .}$ The general formula ${\displaystyle (B\circ A)(\mathbf {x} )=B(A(\mathbf {x} ))}$) that defines the function composition is instanced here as a specific case of associativity of matrix product (see § Associativity below):

${\displaystyle (\mathbf {BA} )\mathbf {x} =\mathbf {B} (\mathbf {Ax} )=\mathbf {BAx} .}$

Geometric rotations

Using a Cartesian coordinate system in a Euclidean plane, the rotation by an angle ${\displaystyle \alpha }$ around the origin is a linear map. More precisely,

${\displaystyle {\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}}$,

where the source point ${\displaystyle (x,y)}$ and its image ${\displaystyle (x',y')}$ are written as column vectors.

The composition of the rotation by ${\displaystyle \alpha }$ and that by ${\displaystyle \beta }$ then corresponds to the matrix product

${\displaystyle {\begin{bmatrix}\cos \beta &-\sin \beta \\\sin \beta &\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{bmatrix}}={\begin{bmatrix}\cos \beta \cos \alpha -\sin \beta \sin \alpha &-\cos \beta \sin \alpha -\sin b\cos \alpha \\\sin \beta \cos \alpha +\cos \beta \sin \alpha &-\sin \beta \sin \alpha +\cos \beta \cos \alpha \end{bmatrix}}={\begin{bmatrix}\cos(\alpha +\beta )&-\sin(\alpha +\beta )\\\sin(\alpha +\beta )&\cos(\alpha +\beta )\end{bmatrix}}}$,

where appropriate trigonometric identities are employed for the second equality. That is, the composition corresponds to the rotation by angle ${\displaystyle \alpha +\beta }$, as expected.

Resource allocation in economics

The computation of the bottom left entry of ${\displaystyle \mathbf {AB} }$ corresponds to the consideration of all paths (highlighted) from basic commodity ${\displaystyle b_{4}}$ to final product ${\displaystyle f_{1}}$ in the production flow graph.

A factory uses 4 kinds of basic commodities [de], ${\displaystyle b_{1},b_{2},b_{3},b_{4}}$ to produce 3 kinds of intermediate goods, ${\displaystyle m_{1},m_{2},m_{3}}$, which in turn are used to produce 3 kinds of final products, ${\displaystyle f_{1},f_{2},f_{3}}$. The matrices

${\displaystyle \mathbf {A} =\left({\begin{array}{ccc}1&0&1\\2&1&1\\0&1&1\\1&1&2\\\end{array}}\right)}$   and   ${\displaystyle \mathbf {B} =\left({\begin{array}{ccc}1&2&1\\2&3&1\\4&2&2\\\end{array}}\right)}$

provide the amount of basic commodities needed for a given amount of intermediate goods, and the amount of intermediate goods needed for a given amount of final products, respectively. For example, to produce one unit of intermediate good ${\displaystyle m_{1}}$, one unit of basic commodity ${\displaystyle b_{1}}$, two units of ${\displaystyle b_{2}}$, no units of ${\displaystyle b_{3}}$, and one unit of ${\displaystyle b_{4}}$ are needed, corresponding to the first column of ${\displaystyle \mathbf {A} }$.

Using matrix multiplication, compute

${\displaystyle \mathbf {AB} =\left({\begin{array}{ccc}5&4&3\\8&9&5\\\ 6&5&3\\11&9&6\\\end{array}}\right)}$;

this matrix directly provides the amounts of basic commodities needed for given amounts of final goods. For example, the bottom left entry of ${\displaystyle \mathbf {AB} }$ is computed as ${\displaystyle 1\cdot 1+1\cdot 2+2\cdot 4=11}$, reflecting that ${\displaystyle 11}$ units of ${\displaystyle b_{4}}$ are needed to produce one unit of ${\displaystyle f_{1}}$. Indeed, one ${\displaystyle b_{4}}$ unit is needed for ${\displaystyle m_{1}}$, 2 for ${\displaystyle m_{2}}$, and ${\displaystyle 4}$ for each of the two ${\displaystyle m_{3}}$ units that go into the ${\displaystyle f_{1}}$ unit, see picture.

In order to produce e.g. 100 units of the final product ${\displaystyle f_{1}}$, 80 units of ${\displaystyle f_{2}}$, and 60 units of ${\displaystyle f_{3}}$, the necessary amounts of basic goods can be computed as

${\displaystyle (\mathbf {AB} )\left({\begin{array}{c}100\\80\\60\\\end{array}}\right)=\left({\begin{array}{c}1000\\1820\\1180\\2180\\\end{array}}\right)}$,

that is, ${\displaystyle 1000}$ units of ${\displaystyle b_{1}}$, ${\displaystyle 1820}$ units of ${\displaystyle b_{2}}$, ${\displaystyle 1180}$ units of ${\displaystyle b_{3}}$, ${\displaystyle 2180}$ units of ${\displaystyle b_{4}}$ are needed. Similarly, the product matrix ${\displaystyle \mathbf {AB} }$ can be used to compute the needed amounts of basic goods for other final-good amount data.

System of linear equations

The general form of a system of linear equations is

${\displaystyle {\begin{matrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m}\end{matrix}}.}$

Using same notation as above, such a system is equivalent with the single matrix equation

${\displaystyle \mathbf {Ax} =\mathbf {b} .}$

Dot product, bilinear form and inner product

The dot product of two column vectors is the matrix product

${\displaystyle \mathbf {x} ^{\mathsf {T}}\mathbf {y} ,}$

where ${\displaystyle \mathbf {x} ^{\mathsf {T}}}$ is the row vector obtained by transposing ${\displaystyle \mathbf {x} }$ and the resulting 1×1 matrix is identified with its unique entry.

More generally, any bilinear form over a vector space of finite dimension may be expressed as a matrix product

${\displaystyle \mathbf {x} ^{\mathsf {T}}\mathbf {Ay} ,}$

and any inner product may be expressed as

${\displaystyle \mathbf {x} ^{\dagger }\mathbf {Ay} ,}$

where ${\displaystyle \mathbf {x} ^{\dagger }}$ denotes the conjugate transpose of ${\displaystyle \mathbf {x} }$ (conjugate of the transpose, or equivalently transpose of the conjugate).

General properties

Matrix multiplication shares some properties with usual multiplication. However, matrix multiplication is not defined if the number of columns of the first factor differs from the number of rows of the second factor, and it is non-commutative, even when the product remains definite after changing the order of the factors.

Non-commutativity

An operation is commutative if, given two elements A and B such that the product ${\displaystyle \mathbf {A} \mathbf {B} }$ is defined, then ${\displaystyle \mathbf {B} \mathbf {A} }$ is also defined, and ${\displaystyle \mathbf {A} \mathbf {B} =\mathbf {B} \mathbf {A} .}$

If A and B are matrices of respective sizes ${\displaystyle m\times n}$ and ${\displaystyle p\times q}$, then ${\displaystyle \mathbf {A} \mathbf {B} }$ is defined if ${\displaystyle n=p}$, and ${\displaystyle \mathbf {B} \mathbf {A} }$ is defined if ${\displaystyle m=q}$. Therefore, if one of the products is defined, the other is not defined in general. If ${\displaystyle m=q\neq n=p}$, the two products are defined, but have different sizes; thus they cannot be equal. Only if ${\displaystyle m=q=n=p}$, that is, if A and B are square matrices of the same size, are both products defined and of the same size. Even in this case, one has in general

${\displaystyle \mathbf {A} \mathbf {B} \neq \mathbf {B} \mathbf {A} .}$

For example

${\displaystyle {\begin{pmatrix}0&1\\0&0\end{pmatrix}}{\begin{pmatrix}0&0\\1&0\end{pmatrix}}={\begin{pmatrix}1&0\\0&0\end{pmatrix}},}$

but

${\displaystyle {\begin{pmatrix}0&0\\1&0\end{pmatrix}}{\begin{pmatrix}0&1\\0&0\end{pmatrix}}={\begin{pmatrix}0&0\\0&1\end{pmatrix}}.}$

This example may be expanded for showing that, if A is a ${\displaystyle n\times n}$ matrix with entries in a field F, then ${\displaystyle \mathbf {A} \mathbf {B} =\mathbf {B} \mathbf {A} }$ for every ${\displaystyle n\times n}$ matrix B with entries in F, if and only if ${\displaystyle \mathbf {A} =c\,\mathbf {I} }$ where ${\displaystyle c\in F}$, and I is the ${\displaystyle n\times n}$ identity matrix. If, instead of a field, the entries are supposed to belong to a ring, then one must add the condition that c belongs to the center of the ring.

One special case where commutativity does occur is when D and E are two (square) diagonal matrices (of the same size); then DE = ED. Again, if the matrices are over a general ring rather than a field, the corresponding entries in each must also commute with each other for this to hold.

Distributivity

The matrix product is distributive with respect to matrix addition. That is, if A, B, C, D are matrices of respective sizes m × n, n × p, n × p, and p × q, one has (left distributivity)

${\displaystyle \mathbf {A} (\mathbf {B} +\mathbf {C} )=\mathbf {AB} +\mathbf {AC} ,}$

and (right distributivity)

${\displaystyle (\mathbf {B} +\mathbf {C} )\mathbf {D} =\mathbf {BD} +\mathbf {CD} .}$

This results from the distributivity for coefficients by

${\displaystyle \sum _{k}a_{ik}(b_{kj}+c_{kj})=\sum _{k}a_{ik}b_{kj}+\sum _{k}a_{ik}c_{kj}}$

${\displaystyle \sum _{k}(b_{ik}+c_{ik})d_{kj}=\sum _{k}b_{ik}d_{kj}+\sum _{k}c_{ik}d_{kj}.}$

Product with a scalar

If A is a matrix and c a scalar, then the matrices ${\displaystyle c\mathbf {A} }$ and ${\displaystyle \mathbf {A} c}$ are obtained by left or right multiplying all entries of A by c. If the scalars have the commutative property, then ${\displaystyle c\mathbf {A} =\mathbf {A} c.}$

If the product ${\displaystyle \mathbf {AB} }$ is defined (that is, the number of columns of A equals the number of rows of B), then

${\displaystyle c(\mathbf {AB} )=(c\mathbf {A} )\mathbf {B} }$ and ${\displaystyle (\mathbf {A} \mathbf {B} )c=\mathbf {A} (\mathbf {B} c).}$

If the scalars have the commutative property, then all four matrices are equal. More generally, all four are equal if c belongs to the center of a ring containing the entries of the matrices, because in this case, cX = Xc for all matrices X.

These properties result from the bilinearity of the product of scalars:

${\displaystyle c\left(\sum _{k}a_{ik}b_{kj}\right)=\sum _{k}(ca_{ik})b_{kj}}$

${\displaystyle \left(\sum _{k}a_{ik}b_{kj}\right)c=\sum _{k}a_{ik}(b_{kj}c).}$

Transpose

If the scalars have the commutative property, the transpose of a product of matrices is the product, in the reverse order, of the transposes of the factors. That is

${\displaystyle (\mathbf {AB} )^{\mathsf {T}}=\mathbf {B} ^{\mathsf {T}}\mathbf {A} ^{\mathsf {T}}}$

where ^T denotes the transpose, that is the interchange of rows and columns.

This identity does not hold for noncommutative entries, since the order between the entries of A and B is reversed, when one expands the definition of the matrix product.

Complex conjugate

If A and B have complex entries, then

${\displaystyle (\mathbf {AB} )^{*}=\mathbf {A} ^{*}\mathbf {B} ^{*}}$

where ^* denotes the entry-wise complex conjugate of a matrix.

This results from applying to the definition of matrix product the fact that the conjugate of a sum is the sum of the conjugates of the summands and the conjugate of a product is the product of the conjugates of the factors.

Transposition acts on the indices of the entries, while conjugation acts independently on the entries themselves. It results that, if A and B have complex entries, one has

${\displaystyle (\mathbf {AB} )^{\dagger }=\mathbf {B} ^{\dagger }\mathbf {A} ^{\dagger },}$

where ^† denotes the conjugate transpose (conjugate of the transpose, or equivalently transpose of the conjugate).

Associativity

Given three matrices A, B and C, the products (AB)C and A(BC) are defined if and only if the number of columns of A equals the number of rows of B, and the number of columns of B equals the number of rows of C (in particular, if one of the products is defined, then the other is also defined). In this case, one has the associative property

${\displaystyle (\mathbf {AB} )\mathbf {C} =\mathbf {A} (\mathbf {BC} ).}$

As for any associative operation, this allows omitting parentheses, and writing the above products as ${\displaystyle \mathbf {ABC} .}$

This extends naturally to the product of any number of matrices provided that the dimensions match. That is, if A₁, A₂, ..., A_n are matrices such that the number of columns of A_i equals the number of rows of A_{i + 1} for i = 1, ..., n – 1, then the product

${\displaystyle \prod _{i=1}^{n}\mathbf {A} _{i}=\mathbf {A} _{1}\mathbf {A} _{2}\cdots \mathbf {A} _{n}}$

is defined and does not depend on the order of the multiplications, if the order of the matrices is kept fixed.

These properties may be proved by straightforward but complicated summation manipulations. This result also follows from the fact that matrices represent linear maps. Therefore, the associative property of matrices is simply a specific case of the associative property of function composition.

Computational complexity depends on parenthezation

Although the result of a sequence of matrix products does not depend on the order of operation (provided that the order of the matrices is not changed), the computational complexity may depend dramatically on this order.

For example, if A, B and C are matrices of respective sizes 10×30, 30×5, 5×60, computing (AB)C needs 10×30×5 + 10×5×60 = 4,500 multiplications, while computing A(BC) needs 30×5×60 + 10×30×60 = 27,000 multiplications.

Algorithms have been designed for choosing the best order of products, see Matrix chain multiplication. When the number n of matrices increases, it has been shown that the choice of the best order has a complexity of ${\displaystyle O(n\log n).}$

Application to similarity

Any invertible matrix ${\displaystyle \mathbf {P} }$ defines a similarity transformation (on square matrices of the same size as ${\displaystyle \mathbf {P} }$)

${\displaystyle S_{\mathbf {P} }(\mathbf {A} )=\mathbf {P} ^{-1}\mathbf {A} \mathbf {P} .}$

Similarity transformations map product to products, that is

${\displaystyle S_{\mathbf {P} }(\mathbf {AB} )=S_{\mathbf {P} }(\mathbf {A} )S_{\mathbf {P} }(\mathbf {B} ).}$

In fact, one has

${\displaystyle \mathbf {P} ^{-1}(\mathbf {AB} )\mathbf {P} =\mathbf {P} ^{-1}\mathbf {A} (\mathbf {P} \mathbf {P} ^{-1})\mathbf {B} \mathbf {P} =(\mathbf {P} ^{-1}\mathbf {A} \mathbf {P} )(\mathbf {P} ^{-1}\mathbf {B} \mathbf {P} ).}$

Square matrices

Let us denote ${\displaystyle {\mathcal {M}}_{n}(R)}$ the set of n×n square matrices with entries in a ring R, which, in practice, is often a field.

In ${\displaystyle {\mathcal {M}}_{n}(R)}$, the product is defined for every pair of matrices. This makes ${\displaystyle {\mathcal {M}}_{n}(R)}$ a ring, which has the identity matrix I as identity element (the matrix whose diagonal entries are equal to 1 and all other entries are 0). This ring is also an associative R-algebra.

If n > 1, many matrices do not have a multiplicative inverse. For example, a matrix such that all entries of a row (or a column) are 0 does not have an inverse. If it exists, the inverse of a matrix A is denoted A⁻¹, and, thus verifies

${\displaystyle \mathbf {A} \mathbf {A} ^{-1}=\mathbf {A} ^{-1}\mathbf {A} =\mathbf {I} .}$

A matrix that has an inverse is an invertible matrix. Otherwise, it is a singular matrix.

A product of matrices is invertible if and only if each factor is invertible. In this case, one has

${\displaystyle (\mathbf {A} \mathbf {B} )^{-1}=\mathbf {B} ^{-1}\mathbf {A} ^{-1}.}$

When R is commutative, and, in particular, when it is a field, the determinant of a product is the product of the determinants. As determinants are scalars, and scalars commute, one has thus

${\displaystyle \det(\mathbf {AB} )=\det(\mathbf {BA} )=\det(\mathbf {A} )\det(\mathbf {B} ).}$

The other matrix invariants do not behave as well with products. Nevertheless, if R is commutative, AB and BA have the same trace, the same characteristic polynomial, and the same eigenvalues with the same multiplicities. However, the eigenvectors are generally different if AB ≠ BA.

Powers of a matrix

One may raise a square matrix to any nonnegative integer power multiplying it by itself repeatedly in the same way as for ordinary numbers. That is,

${\displaystyle \mathbf {A} ^{0}=\mathbf {I} ,}$

${\displaystyle \mathbf {A} ^{1}=\mathbf {A} ,}$

${\displaystyle \mathbf {A} ^{k}=\underbrace {\mathbf {A} \mathbf {A} \cdots \mathbf {A} } _{k{\text{ times}}}.}$

Computing the kth power of a matrix needs k – 1 times the time of a single matrix multiplication, if it is done with the trivial algorithm (repeated multiplication). As this may be very time consuming, one generally prefers using exponentiation by squaring, which requires less than 2 log₂ k matrix multiplications, and is therefore much more efficient.

An easy case for exponentiation is that of a diagonal matrix. Since the product of diagonal matrices amounts to simply multiplying corresponding diagonal elements together, the kth power of a diagonal matrix is obtained by raising the entries to the power k:

${\displaystyle {\begin{bmatrix}a_{11}&0&\cdots &0\\0&a_{22}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}\end{bmatrix}}^{k}={\begin{bmatrix}a_{11}^{k}&0&\cdots &0\\0&a_{22}^{k}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}^{k}\end{bmatrix}}.}$

Abstract algebra

The definition of matrix product requires that the entries belong to a semiring, and does not require multiplication of elements of the semiring to be commutative. In many applications, the matrix elements belong to a field, although the tropical semiring is also a common choice for graph shortest path problems. Even in the case of matrices over fields, the product is not commutative in general, although it is associative and is distributive over matrix addition. The identity matrices (which are the square matrices whose entries are zero outside of the main diagonal and 1 on the main diagonal) are identity elements of the matrix product. It follows that the n × n matrices over a ring form a ring, which is noncommutative except if n = 1 and the ground ring is commutative.

A square matrix may have a multiplicative inverse, called an inverse matrix. In the common case where the entries belong to a commutative ring R, a matrix has an inverse if and only if its determinant has a multiplicative inverse in R. The determinant of a product of square matrices is the product of the determinants of the factors. The n × n matrices that have an inverse form a group under matrix multiplication, the subgroups of which are called matrix groups. Many classical groups (including all finite groups) are isomorphic to matrix groups; this is the starting point of the theory of group representations.

Computational complexity

Main article: Computational complexity of matrix multiplication

 

Improvement of estimates of exponent ω over time for the computational complexity of matrix multiplication ${\displaystyle O(n^{\omega })}$.

The matrix multiplication algorithm that results from the definition requires, in the worst case, ${\displaystyle n^{3}}$ multiplications and ${\displaystyle (n-1)n^{2}}$ additions of scalars to compute the product of two square n×n matrices. Its computational complexity is therefore ${\displaystyle O(n^{3})}$, in a model of computation for which the scalar operations take constant time (in practice, this is the case for floating point numbers, but not for integers).

Rather surprisingly, this complexity is not optimal, as shown in 1969 by Volker Strassen, who provided an algorithm, now called Strassen's algorithm, with a complexity of ${\displaystyle O(n^{\log _{2}7})\approx O(n^{2.8074}).}$ Strassen's algorithm can be parallelized to further improve the performance. As of December 2020, the best matrix multiplication algorithm is by Josh Alman and Virginia Vassilevska Williams and has complexity O(n^2.3728596). It is not known whether matrix multiplication can be performed in O(n^{2 + o(1)}) time. This would be optimal, since one must read the ${\displaystyle n^{2}}$ elements of a matrix in order to multiply it with another matrix.

Since matrix multiplication forms the basis for many algorithms, and many operations on matrices even have the same complexity as matrix multiplication (up to a multiplicative constant), the computational complexity of matrix multiplication appears throughout numerical linear algebra and theoretical computer science.

Generalizations

Other types of products of matrices include:

• Block matrix multiplication
• Cracovian product, defined as A ∧ B = B^TA
• Frobenius inner product, the dot product of matrices considered as vectors, or, equivalently the sum of the entries of the Hadamard product
• Hadamard product of two matrices of the same size, resulting in a matrix of the same size, which is the product entry-by-entry
• Kronecker product or tensor product, the generalization to any size of the preceding
• Khatri-Rao product and Face-splitting product
• Outer product, also called dyadic product or tensor product of two column matrices, which is ${\displaystyle \mathbf {a} \mathbf {b} ^{\mathsf {T}}}$
• Scalar multiplication

Hartree–Fock method

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Hartree-Fock_method 

 

Electronic structure methods
Valence bond theory
Coulson–Fischer theory Generalized valence bond Modern valence bond
Molecular orbital theory
Hartree–Fock method Semi-empirical quantum chemistry methods Møller–Plesset perturbation theory Configuration interaction Coupled cluster Multi-configurational self-consistent field Quantum chemistry composite methods Quantum Monte Carlo
Density functional theory
Time-dependent density functional theory Thomas–Fermi model Orbital-free density functional theory Linearized augmented-plane-wave method Projector augmented wave method
Electronic band structure
Nearly free electron model Tight binding Muffin-tin approximation k·p perturbation theory Empty lattice approximation GW approximation

In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.

The Hartree–Fock method often assumes that the exact N-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of N spin-orbitals. By invoking the variational method, one can derive a set of N-coupled equations for the N spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system.

Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "self-consistent" with the assumed initial field. Thus, self-consistency was a requirement of the solution. The solutions to the non-linear Hartree–Fock equations also behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below), and hence the terminology continued. The equations are almost universally solved by means of an iterative method, although the fixed-point iteration algorithm does not always converge. This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method.

The Hartree–Fock method finds its typical application in the solution of the Schrödinger equation for atoms, molecules, nanostructures and solids but it has also found widespread use in nuclear physics. (See Hartree–Fock–Bogoliubov method for a discussion of its application in nuclear structure theory). In atomic structure theory, calculations may be for a spectrum with many excited energy levels and consequently the Hartree–Fock method for atoms assumes the wave function is a single configuration state function with well-defined quantum numbers and that the energy level is not necessarily the ground state.

For both atoms and molecules, the Hartree–Fock solution is the central starting point for most methods that describe the many-electron system more accurately.

The rest of this article will focus on applications in electronic structure theory suitable for molecules with the atom as a special case. The discussion here is only for the Restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) doubly occupied. Open-shell systems, where some of the electrons are not paired, can be dealt with by either the restricted open-shell or the unrestricted Hartree–Fock methods.

Brief history

Early semi-empirical methods

The origin of the Hartree–Fock method dates back to the end of the 1920s, soon after the discovery of the Schrödinger equation in 1926. Douglas Hartree's methods were guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R. B. Lindsay, and himself) set in the old quantum theory of Bohr.

In the Bohr model of the atom, the energy of a state with principal quantum number n is given in atomic units as ${\displaystyle E=-1/n^{2}}$. It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defect d as an empirical parameter, the energy levels of a generic atom were well approximated by the formula ${\displaystyle E=-1/(n+d)^{2}}$, in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray region (for example, see the empirical discussion and derivation in Moseley's law). The existence of a non-zero quantum defect was attributed to electron–electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data.

Hartree method

Main article: Hartree equation

In 1927, D. R. Hartree introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions. Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., ab initio. His first proposed method of solution became known as the Hartree method, or Hartree product. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J. C. Slater and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the variational principle to an ansatz (trial wave function) as a product of single-particle functions.

In 1930, Slater and V. A. Fock independently pointed out that the Hartree method did not respect the principle of antisymmetry of the wave function. The Hartree method used the Pauli exclusion principle in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of quantum statistics.

Hartree–Fock

A solution to the lack of anti-symmetry in the Hartree method came when it was shown that a Slater determinant, a determinant of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric property of the exact solution and hence is a suitable ansatz for applying the variational principle. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting exchange. Fock's original method relied heavily on group theory and was too abstract for contemporary physicists to understand and implement. In 1935, Hartree reformulated the method to be more suitable for the purposes of calculation.

The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models. Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the central field approximation, to impose the condition that electrons in the same shell have the same radial part, and to restrict the variational solution to be a spin eigenfunction. Even so, calculating a solution by hand using the Hartree–Fock equations for a medium-sized atom was laborious; small molecules required computational resources far beyond what was available before 1950.

Hartree–Fock algorithm

The Hartree–Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the Born–Oppenheimer approximation. Since there are no known analytic solutions for many-electron systems (there are solutions for one-electron systems such as hydrogenic atoms and the diatomic hydrogen cation), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as iteration, which gives rise to the name "self-consistent field method".

Approximations

The Hartree–Fock method makes five major simplifications in order to deal with this task:

• The Born–Oppenheimer approximation is inherently assumed. The full molecular wave function is actually a function of the coordinates of each of the nuclei, in addition to those of the electrons.
• Typically, relativistic effects are completely neglected. The momentum operator is assumed to be completely non-relativistic.
• The variational solution is assumed to be a linear combination of a finite number of basis functions, which are usually (but not always) chosen to be orthogonal. The finite basis set is assumed to be approximately complete.
• Each energy eigenfunction is assumed to be describable by a single Slater determinant, an antisymmetrized product of one-electron wave functions (i.e., orbitals).
• The mean-field approximation is implied. Effects arising from deviations from this assumption are neglected. These effects are often collectively used as a definition of the term electron correlation. However, the label "electron correlation" strictly spoken encompasses both Coulomb correlation and Fermi correlation, and the latter is an effect of electron exchange, which is fully accounted for in the Hartree–Fock method. Stated in this terminology, the method only neglects the Coulomb correlation. However, this is an important flaw, accounting for (among others) Hartree–Fock's inability to capture London dispersion.

Relaxation of the last two approximations give rise to many so-called post-Hartree–Fock methods.

Variational optimization of orbitals

Algorithmic flowchart illustrating the Hartree–Fock method

The variational theorem states that for a time-independent Hamiltonian operator, any trial wave function will have an energy expectation value that is greater than or equal to the true ground-state wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground-state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the Hartree–Fock limit; i.e., the limit of the Hartree–Fock energy as the basis set approaches completeness. (The other is the full-CI limit, where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant.

The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as spin-orbitals. For an atomic orbital calculation, these are typically the orbitals for a hydrogen-like atom (an atom with only one electron, but the appropriate nuclear charge). For a molecular orbital or crystalline calculation, the initial approximate one-electron wave functions are typically a linear combination of atomic orbitals (LCAO).

The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a unitary transformation between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic-energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear–electronic Coulombic attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method and is equivalent to the fifth simplification in the above list.

Since the Fock operator depends on the orbitals used to construct the corresponding Fock matrix, the eigenfunctions of the Fock operator are in turn new orbitals, which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals is calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed from these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed.

Mathematical formulation

The Fock operator

Main article: Fock matrix

Because the electron–electron repulsion term of the molecular Hamiltonian involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation (outlined under Hartree–Fock algorithm), all of the terms of the exact Hamiltonian except the nuclear–nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below, for closed-shell atoms or molecules (with two electrons in each spatial orbital). The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature.

${\displaystyle {\hat {F}}[\{\phi _{j}\}](1)={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)],}$

where

${\displaystyle {\hat {F}}[\{\phi _{j}\}](1)}$

is the one-electron Fock operator generated by the orbitals ${\displaystyle \phi _{j}}$, and

${\displaystyle {\hat {H}}^{\text{core}}(1)=-{\frac {1}{2}}\nabla _{1}^{2}-\sum _{\alpha }{\frac {Z_{\alpha }}{r_{1\alpha }}}}$

is the one-electron core Hamiltonian. Also

${\displaystyle {\hat {J}}_{j}(1)}$

is the Coulomb operator, defining the electron–electron repulsion energy due to each of the two electrons in the j-th orbital. Finally,

${\displaystyle {\hat {K}}_{j}(1)}$

is the exchange operator, defining the electron exchange energy due to the antisymmetry of the total N-electron wave function. This "exchange energy" operator ${\displaystyle {\hat {K}}}$ is simply an artifact of the Slater determinant. Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation

${\displaystyle {\hat {F}}(1)\phi _{i}(1)=\epsilon _{i}\phi _{i}(1),}$

where ${\displaystyle \phi _{i}(1)}$ are a set of one-electron wave functions, called the Hartree–Fock molecular orbitals.

Linear combination of atomic orbitals

Main article: Basis set (chemistry)

Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a linear combination of atomic orbitals. These atomic orbitals are called Slater-type orbitals. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals, rather than Slater-type orbitals, in the interests of saving large amounts of computation time.

Various basis sets are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the Gram–Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan–Hall equations by converting the overlap matrix effectively to an identity matrix. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the generalized eigenvalue problem, of which the Roothaan–Hall equations are an example.

Numerical stability

Numerical stability can be a problem with this procedure and there are various ways of combatting this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single-electron wave function is calculated, it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used, the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations.

Weaknesses, extensions, and alternatives

Of the five simplifications outlined in the section "Hartree–Fock algorithm", the fifth is typically the most important. Neglect of electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called post-Hartree–Fock methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, Møller–Plesset perturbation theory, treats correlation as a perturbation of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as multi-configurational self-consistent field, configuration interaction, quadratic configuration interaction, and complete active space SCF (CASSCF). Still others (such as variational quantum Monte Carlo) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions.

An alternative to Hartree–Fock calculations used in some cases is density functional theory, which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such hybrid functional method. Another option is to use modern valence bond methods.

Software packages

For a list of software packages known to handle Hartree–Fock calculations, particularly for molecules and solids, see the list of quantum chemistry and solid state physics software.