Cooperative binding

From Wikipedia, the free encyclopedia

Cooperative binding occurs in molecular binding systems containing more than one type, or species, of molecule and in which one of the partners is not mono-valent and can bind more than one molecule of the other species. In general, molecular binding is an interaction between molecules that results in a stable physical association between those molecules.

Cooperative binding occurs in a molecular binding system where two or more ligand molecules can bind to a receptor molecule. Binding can be considered "cooperative" if the actual binding of the first molecule of the ligand to the receptor changes the binding affinity of the second ligand molecule. The binding of ligand molecules to the different sites on the receptor molecule do not constitute mutually independent events. Cooperativity can be positive or negative, meaning that it becomes more or less likely that successive ligand molecules will bind to the receptor molecule.

Cooperative binding is observed in many biopolymers, including proteins and nucleic acids. Cooperative binding has been shown to be the mechanism underlying a large range of biochemical and physiological processes.

History and mathematical formalisms

Christian Bohr and the concept of cooperative binding

In 1904, Christian Bohr studied hemoglobin binding to oxygen under different conditions. When plotting hemoglobin saturation with oxygen as a function of the partial pressure of oxygen, he obtained a sigmoidal (or "S-shaped") curve. This indicates that the more oxygen is bound to hemoglobin, the easier it is for more oxygen to bind - until all binding sites are saturated. In addition, Bohr noticed that increasing CO₂ pressure shifted this curve to the right - i.e. higher concentrations of CO₂ make it more difficult for hemoglobin to bind oxygen. This latter phenomenon, together with the observation that hemoglobin's affinity for oxygen increases with increasing pH, is known as the Bohr effect.

Original figure from Christian Bohr, showing the sigmoidal increase of oxyhemoglobin as a function of the partial pressure of oxygen.

A receptor molecule is said to exhibit cooperative binding if its binding to ligand scales non-linearly with ligand concentration. Cooperativity can be positive (if binding of a ligand molecule increases the receptor's apparent affinity, and hence increases the chance of another ligand molecule binding) or negative (if binding of a ligand molecule decreases affinity and hence makes binding of other ligand molecules less likely). The "fractional occupancy" ${\displaystyle \overline{Y}}$ of a receptor with a given ligand is defined as the quantity of ligand-bound binding sites divided by the total quantity of ligand binding sites:

${\displaystyle \overline{Y}=\frac{[\text{bound sites}]}{[\text{bound sites}]+[\text{unbound sites}]}=\frac{[\text{bound sites}]}{[\text{total sites}]}}$

If ${\displaystyle \overline{Y}=0}$, then the protein is completely unbound, and if ${\displaystyle \overline{Y}=1}$, it is completely saturated. If the plot of ${\displaystyle \overline{Y}}$ at equilibrium as a function of ligand concentration is sigmoidal in shape, as observed by Bohr for hemoglobin, this indicates positive cooperativity. If it is not, no statement can be made about cooperativity from looking at this plot alone.

The concept of cooperative binding only applies to molecules or complexes with more than one ligand binding sites. If several ligand binding sites exist, but ligand binding to any one site does not affect the others, the receptor is said to be non-cooperative. Cooperativity can be homotropic, if a ligand influences the binding of ligands of the same kind, or heterotropic, if it influences binding of other kinds of ligands. In the case of hemoglobin, Bohr observed homotropic positive cooperativity (binding of oxygen facilitates binding of more oxygen) and heterotropic negative cooperativity (binding of CO₂ reduces hemoglobin's facility to bind oxygen.)

Throughout the 20th century, various frameworks have been developed to describe the binding of a ligand to a protein with more than one binding site and the cooperative effects observed in this context.

The Hill equation

The first description of cooperative binding to a multi-site protein was developed by A.V. Hill. Drawing on observations of oxygen binding to hemoglobin and the idea that cooperativity arose from the aggregation of hemoglobin molecules, each one binding one oxygen molecule, Hill suggested a phenomenological equation that has since been named after him:

Hill plot of the Hill equation in red, showing the slope of the curve being the Hill coefficient and the intercept with the x-axis providing the apparent dissociation constant. The green line shows the non-cooperative curve.

${\displaystyle \overline{Y}=\frac{K\cdot [X{]}^n}{1+K\cdot [X{]}^n}=\frac{[X{]}^n}{K^{\ast }+[X{]}^n}=\frac{[X{]}^n}{K_d^n+[X{]}^n}}$

where ${\displaystyle n}$ is the "Hill coefficient", ${\displaystyle [X]}$ denotes ligand concentration, ${\displaystyle K}$ denotes an apparent association constant (used in the original form of the equation), ${\displaystyle K^{\ast }}$ is an empirical dissociation constant, and ${\displaystyle K_d}$ a microscopic dissociation constant (used in modern forms of the equation, and equivalent to an ${\displaystyle {\mathrm{E}\mathrm{C}}_{50}}$). If ${\displaystyle n<1}$, the system exhibits negative cooperativity, whereas cooperativity is positive if ${\displaystyle n>1}$. The total number of ligand binding sites is an upper bound for ${\displaystyle n}$. The Hill equation can be linearized as:

${\displaystyle \log \frac{\overline{Y}}{1-\overline{Y}}=n\cdot \log [X]-n\cdot \log K_d}$

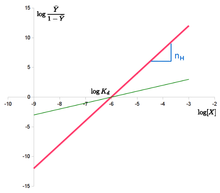
The "Hill plot" is obtained by plotting ${\displaystyle \log \frac{\overline{Y}}{1-\overline{Y}}}$ versus ${\displaystyle \log [X]}$. In the case of the Hill equation, it is a line with slope ${\displaystyle n_H}$ and intercept ${\displaystyle \log (K_d)}$. This means that cooperativity is assumed to be fixed, i.e. it does not change with saturation. It also means that binding sites always exhibit the same affinity, and cooperativity does not arise from an affinity increasing with ligand concentration.

The Adair equation

G.S. Adair found that the Hill plot for hemoglobin was not a straight line, and hypothesized that binding affinity was not a fixed term, but dependent on ligand saturation. Having demonstrated that hemoglobin contained four hemes (and therefore binding sites for oxygen), he worked from the assumption that fully saturated hemoglobin is formed in stages, with intermediate forms with one, two, or three bound oxygen molecules. The formation of each intermediate stage from unbound hemoglobin can be described using an apparent macroscopic association constant ${\displaystyle K_i}$. The resulting fractional occupancy can be expressed as:

${\displaystyle \overline{Y}=\frac{1}{4}\cdot \frac{K_I[X]+2K_{II}[X{]}^2+3K_{III}[X{]}^3+4K_{IV}[X{]}^4}{1+K_I[X]+K_{II}[X{]}^2+K_{III}[X{]}^3+K_{IV}[X{]}^4}}$

Or, for any protein with n ligand binding sites:

${\displaystyle \overline{Y}=\frac{1}{n}\frac{K_I[X]+2K_{II}[X{]}^2+\dots +n{K}_n[X{]}^n}{1+K_I[X]+K_{II}[X{]}^2+\dots +K_n[X{]}^n}}$

where n denotes the number of binding sites and each ${\displaystyle K_i}$ is a combined association constant, describing the binding of i ligand molecules. By combining the Adair treatment with the Hill plot, one arrives at the modern experimental definition of cooperativity (Hill, 1985, Abeliovich, 2005). The resultant Hill coefficient, or more correctly the slope of the Hill plot as calculated from the Adair Equation, can be shown to be the ratio between the variance of the binding number to the variance of the binding number in an equivalent system of non-interacting binding sites. Thus, the Hill coefficient defines cooperativity as a statistical dependence of one binding site on the state of other site(s).

The Klotz equation

Working on calcium binding proteins, Irving Klotz deconvoluted Adair's association constants by considering stepwise formation of the intermediate stages, and tried to express the cooperative binding in terms of elementary processes governed by mass action law. In his framework, ${\displaystyle K_1}$ is the association constant governing binding of the first ligand molecule, ${\displaystyle K_2}$ the association constant governing binding of the second ligand molecule (once the first is already bound) etc. For ${\displaystyle \overline{Y}}$, this gives:

${\displaystyle \overline{Y}=\frac{1}{n}\frac{K_1[X]+2K_1{K}_2[X{]}^2+\dots +n\left(K_1{K}_2\dots K_n\right)[X{]}^n}{1+K_1[X]+K_1{K}_2[X{]}^2+\dots +\left(K_1{K}_2\dots K_n\right)[X{]}^n}}$

It is worth noting that the constants ${\displaystyle K_1}$, ${\displaystyle K_2}$ and so forth do not relate to individual binding sites. They describe how many binding sites are occupied, rather than which ones. This form has the advantage that cooperativity is easily recognised when considering the association constants. If all ligand binding sites are identical with a microscopic association constant ${\displaystyle K}$, one would expect ${\displaystyle K_1=nK,K_2=\frac{n-1}{2}K,\dots K_n=\frac{1}{n}K}$ (that is ${\displaystyle K_i=\frac{n-i+1}{i}K}$) in the absence of cooperativity. We have positive cooperativity if ${\displaystyle K_i}$ lies above these expected values for ${\displaystyle i>1}$.

The Klotz equation (which is sometimes also called the Adair-Klotz equation) is still often used in the experimental literature to describe measurements of ligand binding in terms of sequential apparent binding constants.

Pauling equation

By the middle of the 20th century, there was an increased interest in models that would not only describe binding curves phenomenologically, but offer an underlying biochemical mechanism. Linus Pauling reinterpreted the equation provided by Adair, assuming that his constants were the combination of the binding constant for the ligand (${\displaystyle K}$ in the equation below) and energy coming from the interaction between subunits of the cooperative protein (${\displaystyle \alpha }$ below). Pauling actually derived several equations, depending on the degree of interaction between subunits. Based on wrong assumptions about the localization of hemes, he opted for the wrong one to describe oxygen binding by hemoglobin, assuming the subunit were arranged in a square. The equation below provides the equation for a tetrahedral structure, which would be more accurate in the case of hemoglobin:

${\displaystyle \overline{Y}=\frac{K[X]+3\alpha K^2[X{]}^2+3\alpha {}^3{K}^3[X{]}^3+\alpha {}^6{K}^4[X{]}^4}{1+4K[X]+6\alpha K^2[X{]}^2+4\alpha {}^3{K}^3[X{]}^3+\alpha {}^6{K}^4[X{]}^4}}$

The KNF model

Based on results showing that the structure of cooperative proteins changed upon binding to their ligand, Daniel Koshland and colleagues refined the biochemical explanation of the mechanism described by Pauling. The Koshland-Némethy-Filmer (KNF) model assumes that each subunit can exist in one of two conformations: active or inactive. Ligand binding to one subunit would induce an immediate conformational change of that subunit from the inactive to the active conformation, a mechanism described as "induced fit". Cooperativity, according to the KNF model, would arise from interactions between the subunits, the strength of which varies depending on the relative conformations of the subunits involved. For a tetrahedric structure (they also considered linear and square structures), they proposed the following formula:

${\displaystyle \overline{Y}=\frac{K_{AB}^3(K_X{K}_t[X])+3K_{AB}^4{K}_{BB}(K_X{K}_t[X]{)}^2+3K_{AB}^3{K}_{BB}^3(K_X{K}_t[X]{)}^3+K_{BB}^6(K_X{K}_t[X]{)}^4}{1+4K_{AB}^3(K_X{K}_t[X])+6K_{AB}^4{K}_{BB}(K_X{K}_t[X]{)}^2+4K_{AB}^3{K}_{BB}^3(K_X{K}_t[X]{)}^3+K_{BB}^6(K_X{K}_t[X]{)}^4}}$

Where ${\displaystyle K_X}$ is the constant of association for X, ${\displaystyle K_t}$ is the ratio of B and A states in the absence of ligand ("transition"), ${\displaystyle K_{AB}}$ and ${\displaystyle K_{BB}}$ are the relative stabilities of pairs of neighbouring subunits relative to a pair where both subunits are in the A state (Note that the KNF paper actually presents ${\displaystyle N_s}$, the number of occupied sites, which is here 4 times ${\displaystyle \overline{Y}}$).

The MWC model

Monod-Wyman-Changeux model reaction scheme of a protein made up of two protomers. The protomer can exist under two states, each with a different affinity for the ligand. L is the ratio of states in the absence of ligand, c is the ratio of affinities.

 

Energy diagram of a Monod-Wyman-Changeux model of a protein made up of two protomers. The larger affinity of the ligand for the R state means that the latter is preferentially stabilized by the binding.

The Monod-Wyman-Changeux (MWC) model for concerted allosteric transitions went a step further by exploring cooperativity based on thermodynamics and three-dimensional conformations. It was originally formulated for oligomeric proteins with symmetrically arranged, identical subunits, each of which has one ligand binding site. According to this framework, two (or more) interconvertible conformational states of an allosteric protein coexist in a thermal equilibrium. The states - often termed tense (T) and relaxed (R) - differ in affinity for the ligand molecule. The ratio between the two states is regulated by the binding of ligand molecules that stabilizes the higher-affinity state. Importantly, all subunits of a molecule change states at the same time, a phenomenon known as "concerted transition".

The allosteric isomerisation constant L describes the equilibrium between both states when no ligand molecule is bound: ${\displaystyle L=\frac{\left[T_0\right]}{\left[R_0\right]}}$. If L is very large, most of the protein exists in the T state in the absence of ligand. If L is small (close to one), the R state is nearly as populated as the T state. The ratio of dissociation constants for the ligand from the T and R states is described by the constant c: ${\displaystyle c=\frac{K_d^R}{K_d^T}}$. If ${\displaystyle c=1}$, both R and T states have the same affinity for the ligand and the ligand does not affect isomerisation. The value of c also indicates how much the equilibrium between T and R states changes upon ligand binding: the smaller c, the more the equilibrium shifts towards the R state after one binding. With ${\displaystyle \alpha =\frac{[X]}{K_d^R}}$, fractional occupancy is described as:

${\displaystyle \overline{Y}=\frac{\alpha (1+\alpha {)}^{n-1}+Lc\alpha (1+c\alpha {)}^{n-1}}{(1+\alpha {)}^n+L(1+c\alpha {)}^n}}$

The sigmoid Hill plot of allosteric proteins can then be analysed as a progressive transition from the T state (low affinity) to the R state (high affinity) as the saturation increases. The slope of the Hill plot also depends on saturation, with a maximum value at the inflexion point. The intercepts between the two asymptotes and the y-axis allow to determine the affinities of both states for the ligand.

Hill plot of the MWC binding function in red, of the pure T and R state in green. As the conformation shifts from T to R, so does the binding function. The intercepts with the x-axis provide the apparent dissociation constant as well as the microscopic dissociation constants of R and T states.

In proteins, conformational change is often associated with activity, or activity towards specific targets. Such activity is often what is physiologically relevant or what is experimentally measured. The degree of conformational change is described by the state function ${\displaystyle \overline{R}}$, which denotes the fraction of protein present in the ${\displaystyle R}$ state. As the energy diagram illustrates, ${\displaystyle \overline{R}}$ increases as more ligand molecules bind. The expression for ${\displaystyle \overline{R}}$ is:

${\displaystyle \overline{R}=\frac{(1+\alpha {)}^n}{(1+\alpha {)}^n+L(1+c\alpha {)}^n}}$

A crucial aspect of the MWC model is that the curves for ${\displaystyle \overline{Y}}$ and ${\displaystyle \overline{R}}$ do not coincide, i.e. fractional saturation is not a direct indicator of conformational state (and hence, of activity). Moreover, the extents of the cooperativity of binding and the cooperativity of activation can be very different: an extreme case is provide by the bacteria flagella motor with a Hill coefficient of 1.7 for the binding and 10.3 for the activation. The supra-linearity of the response is sometimes called ultrasensitivity.

If an allosteric protein binds to a target that also has a higher affinity for the R state, then target binding further stabilizes the R state, hence increasing ligand affinity. If, on the other hand, a target preferentially binds to the T state, then target binding will have a negative effect on ligand affinity. Such targets are called allosteric modulators.

Since its inception, the MWC framework has been extended and generalized. Variations have been proposed, for example to cater for proteins with more than two states, proteins that bind to several types of ligands or several types of allosteric modulators  and proteins with non-identical subunits or ligand-binding sites.

Examples

The list of molecular assemblies that exhibit cooperative binding of ligands is very large, but some examples are particularly notable for their historical interest, their unusual properties, or their physiological importance.

Cartoon representation of the protein hemoglobin in its two conformations: "tensed (T)" on the left corresponding to the deoxy form (derived from PDB id:11LFL) and "relaxed (R)" on the right corresponding to the oxy form (derived from PDB id:1LFT).

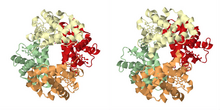
As described in the historical section, the most famous example of cooperative binding is hemoglobin. Its quaternary structure, solved by Max Perutz using X-ray diffraction, exhibits a pseudo-symmetrical tetrahedron carrying four binding sites (hemes) for oxygen. Many other molecular assemblies exhibiting cooperative binding have been studied in great detail.

Multimeric enzymes

The activity of many enzymes is regulated by allosteric effectors. Some of these enzymes are multimeric and carry several binding sites for the regulators.

Threonine deaminase was one of the first enzymes suggested to behave like hemoglobin and shown to bind ligands cooperatively. It was later shown to be a tetrameric protein.

Another enzyme that has been suggested early to bind ligands cooperatively is aspartate trans-carbamylase. Although initial models were consistent with four binding sites, its structure was later shown to be hexameric by William Lipscomb and colleagues.

Ion channels

Most ion channels are formed of several identical or pseudo-identical monomers or domains, arranged symmetrically in biological membranes. Several classes of such channels whose opening is regulated by ligands exhibit cooperative binding of these ligands.

It was suggested as early as 1967 (when the exact nature of those channels was still unknown) that the nicotinic acetylcholine receptors bound acetylcholine in a cooperative manner due to the existence of several binding sites. The purification of the receptor and its characterization demonstrated a pentameric structure with binding sites located at the interfaces between subunits, confirmed by the structure of the receptor binding domain.

Inositol triphosphate (IP3) receptors form another class of ligand-gated ion channels exhibiting cooperative binding. The structure of those receptors shows four IP3 binding sites symmetrically arranged.

Multi-site molecules

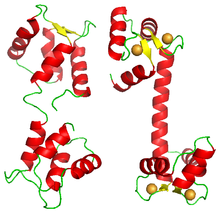
Although most proteins showing cooperative binding are multimeric complexes of homologous subunits, some proteins carry several binding sites for the same ligand on the same polypeptide. One such example is calmodulin. One molecule of calmodulin binds four calcium ions cooperatively. Its structure presents four EF-hand domains, each one binding one calcium ion. The molecule does not display a square or tetrahedron structure, but is formed of two lobes, each carrying two EF-hand domains.

Cartoon representation of the protein Calmodulin in its two conformation: "closed" on the left (derived from PDB id: 1CFD) and "open" on the right (derived from PDB id: 3CLN). The open conformation is represented bound with 4 calcium ions (orange spheres).

Transcription factors

Cooperative binding of proteins onto nucleic acids has also been shown. A classical example is the binding of the lambda phage repressor to its operators, which occurs cooperatively. Other examples of transcription factors exhibit positive cooperativity when binding their target, such as the repressor of the TtgABC pumps (n=1.6), as well as conditional cooperativity exhibited by the transcription factors HOXA11 and FOXO1.

Conversely, examples of negative cooperativity for the binding of transcription factors were also documented, as for the homodimeric repressor of the Pseudomonas putida cytochrome P450cam hydroxylase operon (n=0.56).

Conformational spread and binding cooperativity

Early on, it has been argued that some proteins, especially those consisting of many subunits, could be regulated by a generalized MWC mechanism, in which the transition between R and T state is not necessarily synchronized across the entire protein. In 1969, Wyman proposed such a model with "mixed conformations" (i.e. some protomers in the R state, some in the T state) for respiratory proteins in invertebrates.

Following a similar idea, the conformational spread model by Duke and colleagues subsumes both the KNF and the MWC model as special cases. In this model, a subunit does not automatically change conformation upon ligand binding (as in the KNF model), nor do all subunits in a complex change conformations together (as in the MWC model). Conformational changes are stochastic with the likelihood of a subunit switching states depending on whether or not it is ligand bound and on the conformational state of neighbouring subunits. Thus, conformational states can "spread" around the entire complex.

Impact of upstream and downstream components on module's ultrasensitivity

In a living cell, ultrasensitive modules are embedded in a bigger network with upstream and downstream components. This components may constrain the range of inputs that the module will receive as well as the range of the module's outputs that network will be able to detect. The sensitivity of a modular system is affected by these restrictions. The dynamic range limitations imposed by downstream components can produce effective sensitivities much larger than that of the original module when considered in isolation.

Creoles of color

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Creoles_of_color 

 

Total population
Indeterminable
Regions with significant populations
New Orleans, Louisiana, Texas, Nevada, Alabama, Maryland, Florida, Georgia, Detroit, Chicago, New York, Los Angeles and San Francisco
Languages
English, French, Spanish and Louisiana Creole (Kouri-Vini)
Religion
Predominantly Roman Catholic, Protestant; some practice Voodoo

The Creoles of color are a historic ethnic group of Creole people that developed in the former French and Spanish colonies of Louisiana (especially in the city of New Orleans), Mississippi, Alabama, and Northwestern Florida, in what is now the United States. French colonists in Louisiana first used the term "Creole" to refer to people born in the colony, rather than in France.

The term "Creoles of color" was typically applied to mixed-race Creoles born from the French and Spanish settlers intermarrying with Africans or from manumitted slaves, forming a class of Gens de couleur libres (free people of color). Today, many of these Creoles of color have assimilated into Black culture, while some chose to remain a separate yet inclusive subsection of the African American ethnic group.

Historical Context

Creole cartoonist George Herriman

Créole is derived from latin and means to "create", and was first used in the "New World" by the Portuguese to describe local goods and products, but was later used by the Spanish during colonial occupation to mean any native inhabitant of the New World. The term Créole was first used by French colonists to distinguish themselves from foreign-born settlers, and later as distinct from Anglo-American settlers. Créole referred to people born in Louisiana whose ancestors were not born in the territory. Colonial documents show that the term Créole was used variously at different times to refer to white people, mixed-race people, and black people, both free-born and enslaved. The "of color" is considered a necessary qualifier, as "Creole"(Créole) did not convey any racial connotation.

During French colonization, social order was divided into three distinct categories: Creole aristocrats (grands habitants); a prosperous, educated group of multi-racial Creoles of European, African and Native American descent (bourgeoisie); and the far larger class of African slaves and Creole peasants (petits habitants). French Law regulated interracial conduct within the colony. An example of such laws are the Louisiana Code Noir. Though interracial relations were legally forbidden, or heavily restricted, they were not uncommon. Mixed-race Creoles of color became identified as a distinct ethnic group, Gens de couleur libres (free persons of color), and were granted their free-person status by the Louisiana Supreme Court in 1810. Some have suggested certain social markers of creole identity as being of Catholic faith, having a strong work ethic, being an avid fan of literature, and being fluent in French-- standard French, Creole and Cajun are all considered acceptable versions of the French language. For many, being a descendant of the Gens de couleur libres is an identity marker specific to Creoles of color.

Many Creoles of color were free-born, and their descendants often enjoyed many of the same privileges that whites did, including (but not limited to) property ownership, formal education, and service in the militia. During the antebellum period, their society was structured along class lines and they tended to marry within their group. While it was not illegal, it was a social taboo for Creoles of color to marry slaves and it was a rare occurrence. Some of the wealthier and prosperous Creoles of color owned slaves themselves. Other Creoles of color, such as Thomy Lafon, used their social position to support the abolitionist cause.

Another Creole of color, wealthy planter Francis E. Dumas, emancipated all of his slaves in 1863 and organized them into a company in the Second Regiment of the Louisiana Native Guards, in which he served as an officer.

Migration

First Wave

The first wave of creole migration occurred between 1840 and 1890 with the majority of migrants fleeing to ethnic-dominant outskirts of larger U.S. cities and abroad where race was more fluid.

Second Wave

The reclassification of Creoles of color as black prompted the second migratory wave of Creoles of color between 1920 and 1940.

Military

Creoles of Color had been members of the militia for decades under both French and Spanish control of the colony of Louisiana. For example, around 80 free Creoles of Color were recruited into the militia that participated in the Battle of Baton Rouge in 1779. 69 After the United States made the Louisiana Purchase in 1803 and acquired the large territory west of the Mississippi, the Creoles of color in New Orleans volunteered their services and pledged their loyalty to their new country. They also took an oath of loyalty to William C. C. Claiborne, the Louisiana Territorial Governor appointed by President Thomas Jefferson.

Months after the colony became part of the United States, Claiborne's administration was faced with a dilemma previously unknown in the U.S.; integration in the military by incorporating entire units of previously established "colored" militia. In a February 20, 1804, letter, Secretary of War Henry Dearborn wrote to Claiborne saying, "…it would be prudent not to increase the Corps, but to diminish, if it could be done without giving offense…"  A decade later, the militia of color that remained volunteered to take up arms when the British began landing troops on American soil outside of New Orleans in December 1814. This was the commencement of the Battle of New Orleans.

After the Louisiana Purchase, many Creoles of color lost their favorable social status, despite their service to the militia and their social status prior to the U.S. takeover. The territory and New Orleans became the destination of many migrants from the United States, as well as new immigrants. Migrants from the South imposed their caste system. In this new caste system, all people with African ancestry or visible African features were classified as black, and therefore categorized as second class citizens, regardless of their education, property ownership, or previous status in French society. Former free Creoles of Color were relegated to the ranks of emancipated slaves.

Creole Marianne Celeste Dragon

A notable creole family was that of Andrea Dimitry. Dimitry was a Greek immigrant who married Marianne Céleste Dragon a woman of African and Greek ancestry around 1799. Their son creole author and educator Alexander Dimitry was the first person of color to represent the United States as Ambassador to Costa Rica and Nicaragua. He was also the first superintendent of schools in Louisiana. Andrea Dimitry's children were upper-class elite creole. They were mostly educated at Georgetown University. One of his daughters married into the English royal House of Stuart. Some of the creole children were prominent members of the Confederate Government during the American Civil War.

Activism

With the advantage of having been better educated than the new freedmen, many Creoles of color were active in the struggle for civil rights and served in political office during Reconstruction, helping to bring freedmen into the political system. During late Reconstruction, white Democrats regained political control of state legislatures across the former Confederate states by intimidation of blacks and other Republicans at the polls. Through the late nineteenth century, they worked to impose white supremacy under Jim Crow laws and customs. They disfranchised the majority of blacks, especially by creating barriers to voter registration through devices such as poll taxes, literacy tests, grandfather clauses, etc., stripping African Americans, including Creoles of color, of political power.

Creoles of color were among the African Americans who were limited when the U.S. Supreme Court ruled in the case of Plessy v. Ferguson in 1896, deciding that "separate but equal" accommodations were constitutional. It permitted states to impose Jim Crow rules on federal railways and later interstate buses.

On June 14, 2013, Louisiana Governor Bobby Jindal signed into law Act 276, creating the "prestige" license plate stating "I'm Creole", in honor of the Creoles' contributions, culture, and heritage.

Education

It was common for wealthy francophone Gens de couleur to study in Europe, with some opting to not return due to greater liberties in France. When not educated abroad, or in whites-only schools in the United States by virtue of passing, Creoles of color were often homeschooled or enrolled in private schools. These private schools were often financed and staffed by affluent Creoles of color. For example, L'Institute Catholique was financed by Madame Marie Couvent with writers Armand Lanusse and Jonnai Questy serving as educators.

In 1850 it was determined that 80% of all Gens de couleur libres were literate; a figure significantly higher than the white population of Louisiana at the time.

Contribution to the arts

Literature

During the antebellum period, well-educated francophone gens de couleur libres contributed extensively to literary collections, such as Les Cenelles, with a significant portion of these works dedicated to describing the conditions of their enslaved compatriots. One example of such texts is Le Mulatre (The Mulatto) by Victor Séjour, a Creole of color. Other themes approached aspects of love, religion and many texts were likened to French romanticism. In daily newspapers locally and abroad, pieces written by Creoles of color were prominent. Even during the ban on racial commentary during the antebellum period, pieces written by these creoles reformulated existing french themes to subtly critique race relations in Louisiana, while still gaining in popularity among all readers.

Music

Creole jazz musician Sidney Bechet, a virtuoso on the soprano saxophone

Some Creoles of color trained as classical musicians in 19th-century Louisiana. These musicians would often study with those associated with the French Opera House; some traveled to Paris to complete their studies. Creole composers of that time are discussed in Music and Some Highly Musical People by James Monroe Trotter, and Nos Hommes et Notre Histoire by Rodolphe Lucien Desdunes.

 

X-ray optics

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/X-ray_optics 

X-ray optics is the branch of optics that manipulates X-rays instead of visible light. It deals with focusing and other ways of manipulating the X-ray beams for research techniques such as X-ray crystallography, X-ray fluorescence, small-angle X-ray scattering, X-ray microscopy, X-ray phase-contrast imaging, and X-ray astronomy.

Since X-rays and visible light are both electromagnetic waves they propagate in space in the same way, but because of the much higher frequency and photon energy of X-rays they interact with matter very differently. Visible light is easily redirected using lenses and mirrors, but because the real part of the complex refractive index of all materials is very close to 1 for X-rays, they instead tend to initially penetrate and eventually get absorbed in most materials without changing direction much.

X-ray techniques

There are many different techniques used to redirect X-rays, most of them changing the directions by only minute angles. The most common principle used is reflection at grazing incidence angles, either using total external reflection at very small angles or multilayer coatings. Other principles used include diffraction and interference in the form of zone plates, refraction in compound refractive lenses that use many small X-ray lenses in series to compensate by their number for the minute index of refraction, Bragg reflection from a crystal plane in flat or bent crystals.

X-ray beams are often collimated or reduced in size using pinholes or movable slits typically made of tungsten or some other high-Z material. Narrow parts of an X-ray spectrum can be selected with monochromators based on one or multiple Bragg reflections by crystals. X-ray spectra can also be manipulated by having the X-rays pass through a filter (optics). This will typically reduce the low-energy part of the spectrum, and possibly parts above absorption edges of the elements used for the filter.

Focusing optics

Analytical X-ray techniques such as X-ray crystallography, small-angle X-ray scattering, wide-angle X-ray scattering, X-ray fluorescence, X-ray spectroscopy and X-ray photoelectron spectroscopy all benefit from high X-ray flux densities on the samples being investigated. This is achieved by focusing the divergent beam from the X-ray source onto the sample using one out of a range of focusing optical components. This is also useful for scanning probe techniques such as scanning transmission X-ray microscopy and scanning X-ray fluorescence imaging.

Polycapillary optics

A polycapillary lens for focusing X-rays

Polycapillary lenses are arrays of small hollow glass tubes that guide the X-rays with many total external reflections on the inside of the tubes. The array is tapered so that one end of the capillaries points at the X-ray source and the other at the sample. Polycapillary optics are achromatic and thus suitable for scanning fluorescence imaging and other applications where a broad X-ray spectrum is useful. They collect X-rays efficiently for photon energies of 0.1 to 30 keV and can achieve gains of 100 to 10000 in flux over using a pinhole at 100 mm from the X-ray source. Since only X-rays entering the capillaries within a very narrow angle will be totally internally reflected, only X-rays coming from a small spot will be transmitted through the optic. Polycapillary optics cannot image more than one point to another, so they are used for illumination and collection of X-rays.

Zone plates

Main article: Zone plate

Zone plates consist of a substrate with concentric zones of a phase-shifting or absorbing material with zones getting narrower the larger their radius. The zone widths are designed so that a transmitted wave gets constructive interference in a single point giving a focus. Zone plates can be used as condensers to collect light, but also for direct full-field imaging in e.g. an X-ray microscope. Zone plates are highly chromatic and usually designed only for a narrow energy span, making it necessary to have monochromatic X-rays for efficient collection and high-resolution imaging.

Compound refractive lenses

Main article: Compound refractive lens

Since refractive indices at X-ray wavelengths are so close to 1, the focal lengths of normal lenses get impractically long. To overcome this, lenses with very small radii of curvature are used, and they are stacked in long rows, so that the combined focusing power gets appreciable. Since the refractive index is less than 1 for X-rays, these lenses must be concave to achieve focusing, contrary to visible-light lenses, which are convex for a focusing effect. Radii of curvature are typically less than a millimeter, making the usable X-ray beam width at most about 1 mm. To reduce the absorption of X-rays in these stacks, materials with very low atomic number such as beryllium or lithium are typically used. Since the refractive index depends strongly on X-ray wavelength, these lenses are highly chromatic, and the variation of the focal length with wavelength must be taken into account for any application.

Reflection

Designs based on grazing-incidence reflection used in X-ray telescopes include that by Kirkpatrick–Baez, and several by Wolter (Wolter I–IV)

The basic idea is to reflect a beam of X-rays from a surface and to measure the intensity of X-rays reflected in the specular direction (reflected angle equal to incident angle). It has been shown that a reflection off a parabolic mirror followed by a reflection off a hyperbolic mirror leads to the focusing of X-rays. Since the incoming X-rays must strike the tilted surface of the mirror, the collecting area is small. It can, however, be increased by nesting arrangements of mirrors inside each other.

The ratio of reflected intensity to incident intensity is the X-ray reflectivity for the surface. If the interface is not perfectly sharp and smooth, the reflected intensity will deviate from that predicted by the Fresnel reflectivity law. The deviations can then be analyzed to obtain the density profile of the interface normal to the surface. For films with multiple layers, X-ray reflectivity may show oscillations with wavelength, analogous to the Fabry–Pérot effect. These oscillations can be used to infer layer thicknesses and other properties.

Diffraction

Symmetrically spaced atoms cause re-radiated X-rays to reinforce each other in the specific directions where their path-length difference 2d sin θ equals an integer multiple of the wavelength λ

In X-ray diffraction a beam strikes a crystal and diffracts into many specific directions. The angles and intensities of the diffracted beams indicate a three-dimensional density of electrons within the crystal. X-rays produce a diffraction pattern because their wavelength typically has the same order of magnitude (0.1–10.0 nm) as the spacing between the atomic planes in the crystal.

Each atom re-radiates a small portion of an incoming beam's intensity as a spherical wave. If the atoms are arranged symmetrically (as is found in a crystal) with a separation d, these spherical waves will be in phase (add constructively) only in directions where their path-length difference 2d sin θ is equal to an integer multiple of the wavelength λ. The incoming beam therefore appears to have been deflected by an angle 2θ, producing a reflection spot in the diffraction pattern.

X-ray diffraction is a form of elastic scattering in the forward direction; the outgoing X-rays have the same energy, and thus the same wavelength, as the incoming X-rays, only with altered direction. By contrast, inelastic scattering occurs when energy is transferred from the incoming X-ray to an inner-shell electron, exciting it to a higher energy level. Such inelastic scattering reduces the energy (or increases the wavelength) of the outgoing beam. Inelastic scattering is useful for probing such electron excitation, but not in determining the distribution of atoms within the crystal.

Longer-wavelength photons (such as ultraviolet radiation) would not have sufficient resolution to determine the atomic positions. At the other extreme, shorter-wavelength photons such as gamma rays are difficult to produce in large numbers, difficult to focus, and interact too strongly with matter, producing particle–antiparticle pairs.

Similar diffraction patterns can be produced by scattering electrons or neutrons. X-rays are usually not diffracted from atomic nuclei, but only from the electrons surrounding them.

Interference

X-ray interference is the addition (superposition) of two or more X-ray waves that results in a new wave pattern. X-ray interference usually refers to the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have the same or nearly the same frequency.

Two non-monochromatic X-ray waves are only fully coherent with each other if they both have exactly the same range of wavelengths and the same phase differences at each of the constituent wavelengths.

The total phase difference is derived from the sum of both the path difference and the initial phase difference (if the X-ray waves are generated from two or more different sources). It can then be concluded whether the X-ray waves reaching a point are in phase (constructive interference) or out of phase (destructive interference).

Technologies

There are a variety of techniques used to funnel X-ray photons to the appropriate location on an X-ray detector:

• Grazing incidence mirrors in a Wolter telescope, or a Kirkpatrick–Baez X-ray reflection microscope.
• Zone plates.
• Bent crystals.
• Normal-incidence mirrors making use of multilayer coatings.
• A normal-incidence lens much like an optical lens, such as a compound refractive lens.
• Microstructured optical arrays, namely, capillary/polycapillary optical systems.
• Coded aperture imaging.
• Modulation collimators.
• X-ray waveguides.

Most X-ray optical elements (with the exception of grazing-incidence mirrors) are very small and must be designed for a particular incident angle and energy, thus limiting their applications in divergent radiation. Although the technology has advanced rapidly, its practical uses outside research are still limited. Efforts are ongoing, however, to introduce X-ray optics in medical X-ray imaging. For instance, one of the applications showing greater promise is in enhancing both the contrast and resolution of mammographic images, compared to conventional anti-scatter grids. Another application is to optimize the energy distribution of the X-ray beam to improve contrast-to-noise ratio compared to conventional energy filtering.

Mirrors for X-ray optics

The mirrors can be made of glass, ceramic, or metal foil, coated by a reflective layer. The most commonly used reflective materials for X-ray mirrors are gold and iridium. Even with these the critical reflection angle is energy dependent. For gold at 1 keV, the critical reflection angle is 2.4°.

The use of X-ray mirrors simultaneously requires:

• the ability to determine the location of the arrival of an X-ray photon in two dimensions,
• a reasonable detection efficiency.

Multilayers for X-Rays

No material has substantial reflection for X-rays, except at very small grazing angles. Multilayers enhance the small reflectivity from a single boundary by adding the small reflected amplitudes from many boundaries coherently in phase. For example, if a single boundary has a reflectivity of R = 10⁻⁴ (amplitude r = 10⁻²), then the addition of 100 amplitudes from 100 boundaries can give reflectivity R close to one. The period Λ of the multilayer that provides the in-phase addition is that of the standing wave produced by the input and output beam, Λ = λ/2 sin θ, where λ is the wavelength, and 2θ the half angle between the two beams. For θ = 90°, or reflection at normal incidence, the period of the multilayer is Λ = λ/2. The shortest period that can be used in a multilayer is limited by the size of the atoms to about 2 nm, corresponding to wavelengths above 4 nm. For shorter wavelength a reduction of the incidence angle θ toward more grazing has to be used.

The materials for multilayers are selected to give the highest possible reflection at each boundary and the smallest absorption or the propagation through the structure. This is usually achieved by light, low-density materials for the spacer layer and a heavier material that produces high contrast. The absorption in the heavier material can be reduced by positioning it close to the nodes of the standing-wave field inside the structure. Good low-absorption spacer materials are Be, C, B, B₄C and Si. Some examples of the heavier materials with good contrast are W, Rh, Ru and Mo.

Applications include:

• normal and grazing-incidence optics for telescopes from EUV to hard X-rays,
• microscopes, beam lines at synchrotron and FEL facilities,
• EUV lithography.

Mo/Si is the material selection used for the near-normal incidence reflectors for EUV lithography.

Hard X-ray mirrors

An X-ray mirror optic for NuStar space telescope working up 79 keV was made using multilayered coatings, computer-aided manufacturing, and other techniques. The mirrors use a tungsten/silicon (W/Si) or platinum/silicon-carbide (Pt/SiC) multicoating on slumped glass, allowing a Wolter telescope design.

Infrared window

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Infrared_window 

 

As the main part of the 'window' spectrum, a clear electromagnetic spectral transmission 'window' can be seen between 8 and 14 μm. A fragmented part of the 'window' spectrum (one might say a louvred part of the 'window') can also be seen in the visible to mid-wavelength infrared between 0.2 and 5.5 μm.

The infrared atmospheric window refers to a region of the Infrared spectrum where there is relatively little absorption of terrestrial thermal radiation by atmospheric gases. The window plays an important role in the atmospheric greenhouse effect by maintaining the balance between incoming solar radiation and outgoing IR to space. In the Earth's atmosphere this window is roughly the region between 8 and 14 μm although it can be narrowed or closed at times and places of high humidity because of the strong absorption in the water vapor continuum or because of blocking by clouds. It covers a substantial part of the spectrum from surface thermal emission which starts at roughly 5 μm. Principally it is a large gap in the absorption spectrum of water vapor. Carbon dioxide plays an important role in setting the boundary at the long wavelength end. Ozone partly blocks transmission in the middle of the window.

The importance of the infrared atmospheric window in the atmospheric energy balance was discovered by George Simpson in 1928, based on G. Hettner's 1918 laboratory studies of the gap in the absorption spectrum of water vapor. In those days, computers were not available, and Simpson notes that he used approximations; he writes about the need for this in order to calculate outgoing IR radiation: "There is no hope of getting an exact solution; but by making suitable simplifying assumptions . . . ." Nowadays, accurate line-by-line computations are possible, and careful studies of the spectroscopy of infrared atmospheric gases have been published.

Mechanisms in the infrared atmospheric window

The principal natural greenhouse gases in order of their importance are water vapor H
₂O, carbon dioxide CO
₂, ozone O
₃, methane CH
₄ and nitrous oxide N
₂O. The concentration of the least common of these, N
₂O, is about 400 ppbV. Other gases which contribute to the greenhouse effect are present at pptV levels. These include the chlorofluorocarbons (CFCs) and hydrofluororcarbons (HFC and HCFCs). As discussed below, a major reason that they are so effective as greenhouse gases is that they have strong vibrational bands that fall in the infrared atmospheric window. IR absorption by CO
₂ at 14.7 μm sets the long wavelength limit of the infrared atmospheric window together with absorption by rotational transitions of H
₂O at slightly longer wavelengths. The short wavelength boundary of the atmospheric IR window is set by absorption in the lowest frequency vibrational bands of water vapor. There is a strong band of ozone at 9.6 μm in the middle of the window which is why it acts as such a strong greenhouse gas. Water vapor has a continuum absorption due to collisional broadening of absorption lines which extends through the window. Local very high humidity can completely block the infrared vibrational window.

Over the Atlas Mountains, interferometrically recorded spectra of outgoing longwave radiation show emission that has arisen from the land surface at a temperature of about 320 K and passed through the atmospheric window, and non-window emission that has arisen mainly from the troposphere at temperatures about 260 K.

Over Côte d'Ivoire, interferometrically recorded spectra of outgoing longwave radiation show emission that has arisen from the cloud tops at a temperature of about 265 K and passed through the atmospheric window, and non-window emission that has arisen mainly from the troposphere at temperatures about 240 K. This means that, at the scarcely absorbed continuum of wavelengths (8 to 14 μm), the radiation emitted, by the Earth's surface into a dry atmosphere, and by the cloud tops, mostly passes unabsorbed through the atmosphere, and is emitted directly to space; there is also partial window transmission in far infrared spectral lines between about 16 and 28 μm. Clouds are excellent emitters of infrared radiation. Window radiation from cloud tops arises at altitudes where the air temperature is low, but as seen from those altitudes, the water vapor content of the air above is much lower than that of the air at the land-sea surface. Moreover, the water vapour continuum absorptivity, molecule for molecule, decreases with pressure decrease. Thus water vapour above the clouds, besides being less concentrated, is also less absorptive than water vapour at lower altitudes. Consequently, the effective window as seen from the cloud-top altitudes is more open, with the result that the cloud tops are effectively strong sources of window radiation; that is to say, in effect the clouds obstruct the window only to a small degree (see another opinion about this, proposed by Ahrens (2009) on page 43).

Importance for life

Without the infrared atmospheric window, the Earth would become much too warm to support life, and possibly so warm that it would lose its water, as Venus did early in Solar System history. Thus, the existence of an atmospheric window is critical to Earth remaining a habitable planet.

As a proposed management strategy for global warming, passive daytime radiative cooling (PDRC) surfaces use the infrared window to send heat back into outer space with the aim of reversing rising temperature increases caused by climate change.

Threats

In recent decades, the existence of the infrared atmospheric window has become threatened by the development of highly unreactive gases containing bonds between fluorine and carbon, sulfur or nitrogen. The impact of these compounds was first discovered by Indian–American atmospheric scientist Veerabhadran Ramanathan in 1975, one year after Roland and Molina's much-more-celebrated paper on the ability of chlorofluorocarbons to destroy stratospheric ozone.

The "stretching frequencies" of bonds between fluorine and other light nonmetals are such that strong absorption in the atmospheric window will always be characteristic of compounds containing such bonds, although fluorides of nonmetals other than carbon, nitrogen or sulfur are short-lived due to hydrolysis. This absorption is strengthened because these bonds are highly polar due to the extreme electronegativity of the fluorine atom. Bonds to other halogens also absorb in the atmospheric window, though much less strongly.

Moreover, the unreactive nature of such compounds that makes them so valuable for many industrial purposes means that they are not removable in the natural circulation of the Earth's lower atmosphere. Extremely small natural sources created by means of radioactive oxidation of fluorite and subsequent reaction with sulfate or carbonate minerals produce via degassing atmospheric concentrations of about 40 ppt for all perfluorocarbons and 0.01 ppt for sulfur hexafluoride, but the only natural ceiling is via photolysis in the mesosphere and upper stratosphere. It is estimated that perfluorocarbons (CF
₄, C
₂F
₆, C
₃F
₈), originating from commercial production of anesthetics, refrigerants, and polymers can stay in the atmosphere for between two thousand six hundred and fifty thousand years.

This means that such compounds have an enormous global warming potential. One kilogram of sulfur hexafluoride will, for example, cause as much warming as 23 tonnes of carbon dioxide over 100 years. Perfluorocarbons are similar in this respect, and even carbon tetrachloride (CCl
₄) has a global warming potential of 1800 compared to carbon dioxide. These compounds still remain highly problematic with an ongoing effort to find substitutes for them.

Binding site

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Binding_site

 

Glucose binds to hexokinase in the active site at the beginning of glycolysis.

In biochemistry and molecular biology, a binding site is a region on a macromolecule such as a protein that binds to another molecule with specificity. The binding partner of the macromolecule is often referred to as a ligand. Ligands may include other proteins (resulting in a protein-protein interaction), enzyme substrates, second messengers, hormones, or allosteric modulators. The binding event is often, but not always, accompanied by a conformational change that alters the protein's function. Binding to protein binding sites is most often reversible (transient and non-covalent), but can also be covalent reversible or irreversible.

Function

Binding of a ligand to a binding site on protein often triggers a change in conformation in the protein and results in altered cellular function. Hence binding site on protein are critical parts of signal transduction pathways. Types of ligands include neurotransmitters, toxins, neuropeptides, and steroid hormones. Binding sites incur functional changes in a number of contexts, including enzyme catalysis, molecular pathway signaling, homeostatic regulation, and physiological function. Electric charge, steric shape and geometry of the site selectively allow for highly specific ligands to bind, activating a particular cascade of cellular interactions the protein is responsible for.

Catalysis

Activation energy is decreased in the presence of an enzyme to catalyze the reaction.

Enzymes incur catalysis by binding more strongly to transition states than substrates and products. At the catalytic binding site, several different interactions may act upon the substrate. These range from electric catalysis, acid and base catalysis, covalent catalysis, and metal ion catalysis. These interactions decrease the activation energy of a chemical reaction by providing favorable interactions to stabilize the high energy molecule. Enzyme binding allows for closer proximity and exclusion of substances irrelevant to the reaction. Side reactions are also discouraged by this specific binding.

Types of enzymes that can perform these actions include oxidoreductases, transferases, hydrolases, lyases, isomerases, and ligases.

For instance, the transferase hexokinase catalyzes the phosphorylation of glucose to make glucose-6-phosphate. Active site residues of hexokinase allow for stabilization of the glucose molecule in the active site and spur the onset of an alternative pathway of favorable interactions, decreasing the activation energy.

Inhibition

Protein inhibition by inhibitor binding may induce obstruction in pathway regulation, homeostatic regulation and physiological function.

Competitive inhibitors compete with substrate to bind to free enzymes at active sites and thus impede the production of the enzyme-substrate complex upon binding. For example, carbon monoxide poisoning is caused by the competitive binding of carbon monoxide as opposed to oxygen in hemoglobin.

Uncompetitive inhibitors, alternatively, bind concurrently with substrate at active sites. Upon binding to an enzyme substrate (ES) complex, an enzyme substrate inhibitor (ESI) complex is formed. Similar to competitive inhibitors, the rate at product formation is decreased also.

Lastly, mixed inhibitors are able to bind to both the free enzyme and the enzyme-substrate complex. However, in contrast to competitive and uncompetitive inhibitors, mixed inhibitors bind to the allosteric site. Allosteric binding induces conformational changes that may increase the protein's affinity for substrate. This phenomenon is called positive modulation. Conversely, allosteric binding that decreases the protein's affinity for substrate is negative modulation.

Types

Active site

Main article: Active site

At the active site, a substrate binds to an enzyme to induce a chemical reaction. Substrates, transition states, and products can bind to the active site, as well as any competitive inhibitors. For example, in the context of protein function, the binding of calcium to troponin in muscle cells can induce a conformational change in troponin. This allows for tropomyosin to expose the actin-myosin binding site to which the myosin head binds to form a cross-bridge and induce a muscle contraction.

In the context of the blood, an example of competitive binding is carbon monoxide which competes with oxygen for the active site on heme. Carbon monoxide's high affinity may outcompete oxygen in the presence of low oxygen concentration. In these circumstances, the binding of carbon monoxide induces a conformation change that discourages heme from binding to oxygen, resulting in carbon monoxide poisoning.

Competitive and noncompetitive enzyme binding at active and regulatory (allosteric) site respectively.

Allosteric site

At the regulatory site, the binding of a ligand may elicit amplified or inhibited protein function. The binding of a ligand to an allosteric site of a multimeric enzyme often induces positive cooperativity, that is the binding of one substrate induces a favorable conformation change and increases the enzyme's likelihood to bind to a second substrate. Regulatory site ligands can involve homotropic and heterotropic ligands, in which single or multiple types of molecule affects enzyme activity respectively.

Enzymes that are highly regulated are often essential in metabolic pathways. For example, phosphofructokinase (PFK), which phosphorylates fructose in glycolysis, is largely regulated by ATP. Its regulation in glycolysis is imperative because it is the committing and rate limiting step of the pathway. PFK also controls the amount of glucose designated to form ATP through the catabolic pathway. Therefore, at sufficient levels of ATP, PFK is allosterically inhibited by ATP. This regulation efficiently conserves glucose reserves, which may be needed for other pathways. Citrate, an intermediate of the citric acid cycle, also works as an allosteric regulator of PFK.

Single- and multi-chain binding sites

Binding sites can be characterized also by their structural features. Single-chain sites (of “monodesmic” ligands, μόνος: single, δεσμός: binding) are formed by a single protein chain, while multi-chain sites (of "polydesmic” ligands, πολοί: many) are frequent in protein complexes, and are formed by ligands that bind more than one protein chain, typically in or near protein interfaces. Recent research shows that binding site structure has profound consequences for the biology of protein complexes (evolution of function, allostery).

Cryptic binding sites

Cryptic binding sites are the binding sites that are transiently formed in an apo form or that are induced by ligand binding. Considering the cryptic binding sites increases the size of the potentially “druggable” human proteome from ~40% to ~78% of disease-associated proteins. The binding sites have been investigated by: support vector machine applied to "CryptoSite" data set, Extension of "CryptoSite" data set, long timescale molecular dynamics simulation with Markov state model and with biophysical experiments, and cryptic-site index that is based on relative accessible surface area.

Binding curves

Sigmoidal versus hyperbolic binding patterns demonstrate cooperative and noncooperative character of enzymes.

Binding curves describe the binding behavior of ligand to a protein. Curves can be characterized by their shape, sigmoidal or hyperbolic, which reflect whether or not the protein exhibits cooperative or noncooperative binding behavior respectively. Typically, the x-axis describes the concentration of ligand and the y-axis describes the fractional saturation of ligands bound to all available binding sites. The Michaelis Menten equation is usually used when determining the shape of the curve. The Michaelis Menten equation is derived based on steady-state conditions and accounts for the enzyme reactions taking place in a solution. However, when the reaction takes place while the enzyme is bound to a substrate, the kinetics play out differently.

Modeling with binding curves are useful when evaluating the binding affinities of oxygen to hemoglobin and myoglobin in the blood. Hemoglobin, which has four heme groups, exhibits cooperative binding. This means that the binding of oxygen to a heme group on hemoglobin induces a favorable conformation change that allows for increased binding favorability of oxygen for the next heme groups. In these circumstances, the binding curve of hemoglobin will be sigmoidal due to its increased binding favorability for oxygen. Since myoglobin has only one heme group, it exhibits noncooperative binding which is hyperbolic on a binding curve.

Applications

Biochemical differences between different organisms and humans are useful for drug development. For instance, penicillin kills bacteria by inhibiting the bacterial enzyme DD-transpeptidase, destroying the development of the bacterial cell wall and inducing cell death. Thus, the study of binding sites is relevant to many fields of research, including cancer mechanisms, drug formulation, and physiological regulation. The formulation of an inhibitor to mute a protein's function is a common form of pharmaceutical therapy.

Methotrexate inhibits dihydrofolate reductase by outcompeting the substrate folic acid. Binding site in blue, inhibitor in green, and substrate in black.

In the scope of cancer, ligands that are edited to have a similar appearance to the natural ligand are used to inhibit tumor growth. For example, Methotrexate, a chemotherapeutic, acts as a competitive inhibitor at the dihydrofolate reductase active site. This interaction inhibits the synthesis of tetrahydrofolate, shutting off production of DNA, RNA and proteins. Inhibition of this function represses neoplastic growth and improves severe psoriasis and adult rheumatoid arthritis.

In cardiovascular illnesses, drugs such as beta blockers are used to treat patients with hypertension. Beta blockers (β-Blockers) are antihypertensive agents that block the binding of the hormones adrenaline and noradrenaline to β1 and β2 receptors in the heart and blood vessels. These receptors normally mediate the sympathetic "fight or flight" response, causing constriction of the blood vessels.

Competitive inhibitors are also largely found commercially. Botulinum toxin, known commercially as Botox, is a neurotoxin causes flaccid paralysis in the muscle due to binding to acetylcholine dependent nerves. This interaction inhibits muscle contractions, giving the appearance of smooth muscle.

Prediction

A number of computational tools have been developed for the prediction of the location of binding sites on proteins. These can be broadly classified into sequence based or structure based. Sequence based methods rely on the assumption that the sequences of functionally conserved portions of proteins such as binding site are conserved. Structure based methods require the 3D structure of the protein. These methods in turn can be subdivided into template and pocket based methods. Template based methods search for 3D similarities between the target protein and proteins with known binding sites. The pocket based methods search for concave surfaces or buried pockets in the target protein that possess features such as hydrophobicity and hydrogen bonding capacity that would allow them to bind ligands with high affinity. Even though the term pocket is used here, similar methods can be used to predict binding sites used in protein-protein interactions that are usually more planar, not in pockets.