Magnetic nanoparticles

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Magnetic_nanoparticles

Magnetic nanoparticles are a class of nanoparticle that can be manipulated using magnetic fields. Such particles commonly consist of two components, a magnetic material, often iron, nickel and cobalt, and a chemical component that has functionality. While nanoparticles are smaller than 1 micrometer in diameter (typically 1–100 nanometers), the larger microbeads are 0.5–500 micrometer in diameter. Magnetic nanoparticle clusters that are composed of a number of individual magnetic nanoparticles are known as magnetic nanobeads with a diameter of 50–200 nanometers. Magnetic nanoparticle clusters are a basis for their further magnetic assembly into magnetic nanochains. The magnetic nanoparticles have been the focus of much research recently because they possess attractive properties which could see potential use in catalysis including nanomaterial-based catalysts, biomedicine and tissue specific targeting, magnetically tunable colloidal photonic crystals, microfluidics, magnetic resonance imaging, magnetic particle imaging, data storage, environmental remediation, nanofluids, optical filters, defect sensor, magnetic cooling and cation sensors.

Properties

The physical and chemical properties of magnetic nanoparticles largely depend on the synthesis method and chemical structure. In most cases, the particles range from 1 to 100 nm in size and may display superparamagnetism.

Types of magnetic nanoparticles

Oxides: ferrites

Ferrite nanoparticles or iron oxide nanoparticles (iron oxides in crystal structure of maghemite or magnetite) are the most explored magnetic nanoparticles up to date. Once the ferrite particles become smaller than 128 nm they become superparamagnetic which prevents self agglomeration since they exhibit their magnetic behavior only when an external magnetic field is applied. The magnetic moment of ferrite nanoparticles can be greatly increased by controlled clustering of a number of individual superparamagnetic nanoparticles into superparamagnetic nanoparticle clusters, namely magnetic nanobeads. With the external magnetic field switched off, the remanence falls back to zero. Just like non-magnetic oxide nanoparticles, the surface of ferrite nanoparticles is often modified by surfactants, silica, silicones or phosphoric acid derivatives to increase their stability in solution.

Ferrites with a shell

TEM image of a maghemite magnetic nanoparticle cluster with silica shell.

The surface of a maghemite or magnetite magnetic nanoparticle is relatively inert and does not usually allow strong covalent bonds with functionalization molecules. However, the reactivity of the magnetic nanoparticles can be improved by coating a layer of silica onto their surface. The silica shell can be easily modified with various surface functional groups via covalent bonds between organo-silane molecules and silica shell. In addition, some fluorescent dye molecules can be covalently bonded to the functionalized silica shell.

Ferrite nanoparticle clusters with narrow size distribution consisting of superparamagnetic oxide nanoparticles (~ 80 maghemite superparamagnetic nanoparticles per bead) coated with a silica shell have several advantages over metallic nanoparticles:

• Higher chemical stability (crucial for biomedical applications)
• Narrow size distribution (crucial for biomedical applications)
• Higher colloidal stability since they do not magnetically agglomerate
• Magnetic moment can be tuned with the nanoparticle cluster size
• Retained superparamagnetic properties (independent of the nanoparticle cluster size)
• Silica surface enables straightforward covalent functionalization

Metallic

Metallic nanoparticles may be beneficial for some technical applications due to their higher magnetic moment whereas oxides (maghemite, magnetite) would be beneficial for biomedical applications. This also implies that for the same moment, metallic nanoparticles can be made smaller than their oxide counterparts. On the other hand, metallic nanoparticles have the great disadvantage of being pyrophoric and reactive to oxidizing agents to various degrees. This makes their handling difficult and enables unwanted side reactions which makes them less appropriate for biomedical applications. Colloid formation for metallic particles is also much more challenging.

Metallic with a shell

Cobalt nanoparticle with graphene shell (note: The individual graphene layers are visible)

The metallic core of magnetic nanoparticles may be passivated by gentle oxidation, surfactants, polymers and precious metals. In an oxygen environment, Co nanoparticles form an anti-ferromagnetic CoO layer on the surface of the Co nanoparticle. Recently, work has explored the synthesis and exchange bias effect in these Co core CoO shell nanoparticles with a gold outer shell. Nanoparticles with a magnetic core consisting either of elementary Iron or Cobalt with a nonreactive shell made of graphene have been synthesized recently. The advantages compared to ferrite or elemental nanoparticles are:

• Higher magnetization
• Higher stability in acidic and basic solution as well as organic solvents
• Chemistry^[28] on the graphene surface via methods already known for carbon nanotubes

Synthesis

Several methods exist for preparing magnetic nanoparticle.

Co-precipitation

Main article: Co-precipitation

Co-precipitation is a facile and convenient way to synthesize iron oxides (either Fe₃O₄ or γ-Fe₂O₃) from aqueous Fe²⁺/Fe³⁺ salt solutions by the addition of a base under inert atmosphere at room temperature or at elevated temperature. The size, shape, and composition of the magnetic nanoparticles very much depends on the type of salts used (e.g.chlorides, sulfates, nitrates), the Fe²⁺/Fe³⁺ ratio, the reaction temperature, the pH value and ionic strength of the media, and the mixing rate with the base solution used to provoke the precipitation. The co-precipitation approach has been used extensively to produce ferrite nanoparticles of controlled sizes and magnetic properties. A variety of experimental arrangements have been reported to facilitate continuous and large–scale co–precipitation of magnetic particles by rapid mixing. Recently, the growth rate of the magnetic nanoparticles was measured in real-time during the precipitation of magnetite nanoparticles by an integrated AC magnetic susceptometer within the mixing zone of the reactants.

Thermal decomposition

Main article: Thermal decomposition

Magnetic nanocrystals with smaller size can essentially be synthesized through the thermal decomposition of alkaline organometallic compounds in high-boiling organic solvents containing stabilizing surfactants.

Microemulsion

Main article: Microemulsion

Using the microemulsion technique, metallic cobalt, cobalt/platinum alloys, and gold-coated cobalt/platinum nanoparticles have been synthesized in reverse micelles of cetyltrimethlyammonium bromide, using 1-butanol as the cosurfactant and octane as the oil phase.

Flame spray synthesis

Using flame spray pyrolysis and varying the reaction conditions, oxides, metal or carbon coated nanoparticles are produced at a rate of > 30 g/h .

Various flame spray conditions and their impact on the resulting nanoparticles

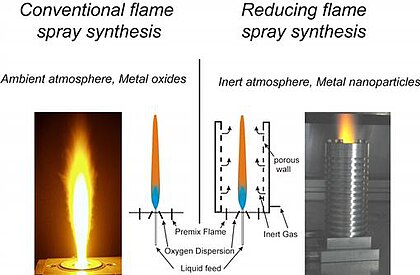Operational layout differences between conventional and reducing flame spray synthesis

Potential applications

A wide variety of potential applications have been envisaged. Since magnetic nanoparticles are expensive to produce, there is interest in their recycling or for highly specialized applications.

The potential and versatility of magnetic chemistry arises from the fast and easy separation of the magnetic nanoparticles, eliminating tedious and costly separation processes usually applied in chemistry. Furthermore, the magnetic nanoparticles can be guided via a magnetic field to the desired location which could, for example, enable pinpoint precision in fighting cancer.

Medical diagnostics and treatments

Magnetic nanoparticles have been examined for use in an experimental cancer treatment called magnetic hyperthermia in which an alternating magnetic field (AMF) is used to heat the nanoparticles. To achieve sufficient magnetic nanoparticle heating, the AMF typically has a frequency between 100–500 kHz, although significant research has been done at lower frequencies as well as frequencies as high as 10 MHz, with the amplitude of the field usually between 8-16kAm⁻¹.

Affinity ligands such as epidermal growth factor (EGF), folic acid, aptamers, lectins etc. can be attached to the magnetic nanoparticle surface with the use of various chemistries. This enables targeting of magnetic nanoparticles to specific tissues or cells. This strategy is used in cancer research to target and treat tumors in combination with magnetic hyperthermia or nanoparticle-delivered cancer drugs. Despite research efforts, however, the accumulation of nanoparticles inside of cancer tumors of all types is sub-optimal, even with affinity ligands. Willhelm et al. conducted a broad analysis of nanoparticle delivery to tumors and concluded that the median amount of injected dose reaching a solid tumor is only 0.7%. The challenge of accumulating large amounts of nanoparticles inside of tumors is arguably the biggest obstacle facing nanomedicine in general. While direct injection is used in some cases, intravenous injection is most often preferred to obtain a good distribution of particles throughout the tumor. Magnetic nanoparticles have a distinct advantage in that they can accumulate in desired regions via magnetically guided delivery, although this technique still needs further development to achieve optimal delivery to solid tumors.

Another potential treatment of cancer includes attaching magnetic nanoparticles to free-floating cancer cells, allowing them to be captured and carried out of the body. The treatment has been tested in the laboratory on mice and will be looked at in survival studies.

Magnetic nanoparticles can be used for the detection of cancer. Blood can be inserted onto a microfluidic chip with magnetic nanoparticles in it. These magnetic nanoparticles are trapped inside due to an externally applied magnetic field as the blood is free to flow through. The magnetic nanoparticles are coated with antibodies targeting cancer cells or proteins. The magnetic nanoparticles can be recovered and the attached cancer-associated molecules can be assayed to test for their existence.

Magnetic nanoparticles can be conjugated with carbohydrates and used for detection of bacteria. Iron oxide particles have been used for the detection of Gram negative bacteria like Escherichia coli and for detection of Gram positive bacteria like Streptococcus suis

Core-shell magnetic nanoparticles, particularly cobalt ferrite, possess antimicrobial properties against hazardous prokaryotic (E. coli, Staphylococcus aureus) and eukaryotic (Candida parapsilosis, Candida albicans) microorganisms. It is known that the size of the magnetic nanoparticles performs a critical role, as the smaller the particles, the more significant the antimicrobial effect.

Other diagnostic uses can be achieved by conjugation of the nanoparticles with oligonucleotides that can either be complementary to a DNA or RNA sequence of interest to detect them, such as pathogenic DNA or products of DNA amplification reactions in the presence of pathogenic DNA, or an aptamer recognizing a molecule of interest. This can lead to detection of pathogens such as virus or bacteria in humans or dangerous chemicals or other substances in the body.

Magnetic immunoassay

Magnetic immunoassay (MIA) is a novel type of diagnostic immunoassay utilizing magnetic nanobeads as labels in lieu of conventional, enzymes, radioisotopes or fluorescent moieties. This assay involves the specific binding of an antibody to its antigen, where a magnetic label is conjugated to one element of the pair. The presence of magnetic nanobeads is then detected by a magnetic reader (magnetometer) which measures the magnetic field change induced by the beads. The signal measured by the magnetometer is proportional to the analyte (virus, toxin, bacteria, cardiac marker, etc.) quantity in the initial sample.

Waste water treatment

Thanks to the easy separation by applying a magnetic field and the very large surface to volume ratio, magnetic nanoparticles have a potential for treatment of contaminated water. In this method, attachment of EDTA-like chelators to carbon coated metal nanomagnets results in a magnetic reagent for the rapid removal of heavy metals from solutions or contaminated water by three orders of magnitude to concentrations as low as micrograms per Litre. Magnetic nanobeads or nanoparticle clusters composed of FDA-approved oxide superparamagnetic nanoparticles (e.g. maghemite, magnetite) hold much potential for waste water treatment since they express excellent biocompatibility which concerning the environmental impacts of the material is an advantage compared to metallic nanoparticles.

Electrochemical sensing

Magneto-electrochemical assays are based on the use of magnetic nanoparticles in electrochemical sensing either by being distributed through a sample where they can collect and preconcentrate the analyte and handled by a magnetic field or by modifying an electrode surface enhancing its conductivity and the affinity with the analyte. Coated-magnetic nanoparticles have a key aspect in electrochemical sensing not only because it facilitates the collecting of analyte but also it allows MNPs to be part of the sensor transduction mechanism. For the manipulation of MNPs in electrochemical sensing has been used magnetic electrode shafts or disposable screen-printed electrodes integrating permanent bonded magnets, aiming to replace magnetic supports or any external magnetic field.

Supported enzymes and peptides

Enzymes, proteins, and other biologically and chemically active substances have been immobilized on magnetic nanoparticles. The immobilization of enzymes on inexpensive, non-toxic and easily synthesized iron magnetic nanoparticles (MNP) has shown great promise due to more stable proteins, better product yield, ease of protein purification and multiple usage as a result of their magnetic susceptibility. They are of interest as possible supports for solid phase synthesis.

This technology is potentially relevant to cellular labelling/cell separation, detoxification of biological fluids, tissue repair, drug delivery, magnetic resonance imaging, hyperthermia and magnetofection.

Random versus site-directed enzyme immobilization

Enzymes immobilized on magnetic nanoparticles (MNP) via random multipoint attachment, result in a heterogeneous protein population with reduced activity due to restriction of substrate access to the active site. Methods based on chemical modifications are now available where MNP can be linked to a protein molecule via a single specific amino acid (such as N- or C- termini), thus avoiding reduction in activity due to the free access of the substrate to the active site. Moreover, site-directed immobilization also avoids modifying catalytic residues. One such common method involves using Alkyne-Azide Click chemistry as both groups are absent in proteins.

Catalyst support

Magnetic nanoparticles are of potential use as a catalyst or catalyst supports. In chemistry, a catalyst support is the material, usually a solid with a high surface area, to which a catalyst is affixed. The reactivity of heterogeneous catalysts occurs at the surface atoms. Consequently, great effort is made to maximize the surface area of a catalyst by distributing it over the support. The support may be inert or participate in the catalytic reactions. Typical supports include various kinds of carbon, alumina, and silica. Immobilizing the catalytic center on top of nanoparticles with a large surface to volume ratio addresses this problem. In the case of magnetic nanoparticles it adds the property of facile a separation. An early example involved a rhodium catalysis attached to magnetic nanoparticles.

In another example, the stable radical TEMPO was attached to the graphene-coated cobalt nanoparticles via a diazonium reaction. The resulting catalyst was then used for the chemoselective oxidation of primary and secondary alcohols.

The catalytic reaction can be conducted in a continuous flow reactor instead of a batch reactor with no remains of the catalyst in the end product. Graphene coated cobalt nanoparticles have been used for that experiment since they exhibit a higher magnetization than Ferrite nanoparticles, which is essential for a fast and clean separation via external magnetic field.

Biomedical imaging

There are many applications for iron-oxide based nanoparticles in concert with magnetic resonance imaging. Magnetic CoPt nanoparticles are being used as an MRI contrast agent for transplanted neural stem cell detection.

Cancer therapy

In magnetic fluid hyperthermia, nanoparticles of different types like Iron oxide, magnetite, maghemite or even gold are injected in tumor and then subjected under a high frequency magnetic field. These nanoparticles produce heat that typically increases tumor temperature to 40-46 °C, which can kill cancer cells. Another major potential of magnetic nanoparticles is the ability to combine heat (hyperthermia) and drug release for a cancer treatment. Numerous studies have shown particle constructs that can be loaded with a drug cargo and magnetic nanoparticles. The most prevalent construct is the "Magnetoliposome", which is a liposome with magnetic nanoparticles typically embedded in the lipid bilayer. Under an alternating magnetic field, the magnetic nanoparticles are heated, and this heat permeabilizes the membrane. This causes release of the loaded drug. This treatment option has a lot of potential as the combination of hyperthermia and drug release is likely to treat tumors better than either option alone, but it is still under development.

Information storage

See also: MRAM

A promising candidate for high-density storage is the face-centered tetragonal phase FePt alloy. Grain sizes can be as small as 3 nanometers. If it's possible to modify the MNPs at this small scale, the information density that can be achieved with this media could easily surpass 1 Terabyte per square inch.

Genetic engineering

Magnetic nanoparticles can be used for a variety of genetics applications. One application is the rapid isolation of DNA and mRNA. In one application, the magnetic bead is attached to a poly T tail. When mixed with mRNA, the poly A tail of the mRNA will attach to the bead's poly T tail and the isolation takes place simply by placing a magnet on the side of the tube and pouring out the liquid. Magnetic beads have also been used in plasmid assembly. Rapid genetic circuit construction has been achieved by the sequential addition of genes onto a growing genetic chain, using nanobeads as an anchor. This method has been shown to be much faster than previous methods, taking less than an hour to create functional multi-gene constructs in vitro.

Physical modeling

There are a variety of mathematical models to describe the dynamics of the rotations of magnetic nanoparticles. Simple models include the Langevin function and the Stoner-Wohlfarth model which describe the magnetization of a nanoparticle at equilibrium. The Debye/Rosenszweig model can be used for low amplitude or high frequency oscillations of particles, which assumes linear response of the magnetization to an oscillating magnetic field. Non-equilibrium approaches include the Langevin equation formalism and the Fokker-Planck equation formalism, and these have been developed extensively to model applications such as magnetic nanoparticle hyperthermia, magnetic nanoparticle imaging (MPI), magnetic spectroscopy  and biosensing etc.

Natural number

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Natural_number

Example of a natural number: 6. There are 6 apples in this picture and 6 is shown as an arabic numeral.

In mathematics, the natural numbers are the numbers 1, 2, 3, etc., possibly including 0 as well. Some definitions, including the standard ISO 80000-2, begin the natural numbers with 0, corresponding to the non-negative integers 0, 1, 2, 3, ..., whereas others start with 1, corresponding to the positive integers 1, 2, 3, ... Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). In common language, particularly in primary school education, natural numbers may be called counting numbers to intuitively exclude the negative integers and zero, and also to contrast the discreteness of counting to the continuity of measurement—a hallmark characteristic of real numbers.

The natural numbers can be used for counting (as in "there are six coins on the table"), in which case they serve as cardinal numbers. They may also be used for ordering (as in "this is the third largest city in the country"), in which case they serve as ordinal numbers. Natural numbers are sometimes used as labels—also known as nominal numbers, (e.g. jersey numbers in sports)—which do not have the properties of numbers in a mathematical sense.

The natural numbers form a set, often symbolized as $\mathbb{N}$. Many other number sets are built by successively extending the set of natural numbers: the integers, by including an additive identity 0 (if not yet in) and an additive inverse −n for each nonzero natural number n; the rational numbers, by including a multiplicative inverse ${\displaystyle 1/n}$ for each nonzero integer n (and also the product of these inverses by integers); the real numbers by including the limits of Cauchy sequences of rationals; the complex numbers, by adjoining to the real numbers a square root of −1 (and also the sums and products thereof); and so on. This chain of extensions canonically embeds the natural numbers in the other number systems.

Properties of the natural numbers, such as divisibility and the distribution of prime numbers, are studied in number theory. Problems concerning counting and ordering, such as partitioning and enumerations, are studied in combinatorics.

History

Ancient roots

The Ishango bone (on exhibition at the Royal Belgian Institute of Natural Sciences)is believed to have been used 20,000 years ago for natural number arithmetic.

The most primitive method of representing a natural number is to put down a mark for each object. Later, a set of objects could be tested for equality, excess or shortage—by striking out a mark and removing an object from the set.

The first major advance in abstraction was the use of numerals to represent numbers. This allowed systems to be developed for recording large numbers. The ancient Egyptians developed a powerful system of numerals with distinct hieroglyphs for 1, 10, and all powers of 10 up to over 1 million. A stone carving from Karnak, dating back from around 1500 BCE and now at the Louvre in Paris, depicts 276 as 2 hundreds, 7 tens, and 6 ones; and similarly for the number 4,622. The Babylonians had a place-value system based essentially on the numerals for 1 and 10, using base sixty, so that the symbol for sixty was the same as the symbol for one—its value being determined from context.

A much later advance was the development of the idea that 0 can be considered as a number, with its own numeral. The use of a 0 digit in place-value notation (within other numbers) dates back as early as 700 BCE by the Babylonians, who omitted such a digit when it would have been the last symbol in the number. The Olmec and Maya civilizations used 0 as a separate number as early as the 1st century BCE, but this usage did not spread beyond Mesoamerica. The use of a numeral 0 in modern times originated with the Indian mathematician Brahmagupta in 628 CE. However, 0 had been used as a number in the medieval computus (the calculation of the date of Easter), beginning with Dionysius Exiguus in 525 CE, without being denoted by a numeral. Standard Roman numerals do not have a symbol for 0; instead, nulla (or the genitive form nullae) from nullus, the Latin word for "none", was employed to denote a 0 value.

The first systematic study of numbers as abstractions is usually credited to the Greek philosophers Pythagoras and Archimedes. Some Greek mathematicians treated the number 1 differently than larger numbers, sometimes even not as a number at all. Euclid, for example, defined a unit first and then a number as a multitude of units, thus by his definition, a unit is not a number and there are no unique numbers (e.g., any two units from indefinitely many units is a 2).

Independent studies on numbers also occurred at around the same time in India, China, and Mesoamerica.

Modern definitions

In 19th century Europe, there was mathematical and philosophical discussion about the exact nature of the natural numbers. Henri Poincaré stated that axioms can only be demonstrated in their finite application, and concluded that it is "the power of the mind" which allows conceiving of the indefinite repetition of the same act. Leopold Kronecker summarized his belief as "God made the integers, all else is the work of man".

The constructivists saw a need to improve upon the logical rigor in the foundations of mathematics. In the 1860s, Hermann Grassmann suggested a recursive definition for natural numbers, thus stating they were not really natural—but a consequence of definitions. Later, two classes of such formal definitions were constructed; later still, they were shown to be equivalent in most practical applications.

Set-theoretical definitions of natural numbers were initiated by Frege. He initially defined a natural number as the class of all sets that are in one-to-one correspondence with a particular set. However, this definition turned out to lead to paradoxes, including Russell's paradox. To avoid such paradoxes, the formalism was modified so that a natural number is defined as a particular set, and any set that can be put into one-to-one correspondence with that set is said to have that number of elements.

The second class of definitions was introduced by Charles Sanders Peirce, refined by Richard Dedekind, and further explored by Giuseppe Peano; this approach is now called Peano arithmetic. It is based on an axiomatization of the properties of ordinal numbers: each natural number has a successor and every non-zero natural number has a unique predecessor. Peano arithmetic is equiconsistent with several weak systems of set theory. One such system is ZFC with the axiom of infinity replaced by its negation. Theorems that can be proved in ZFC but cannot be proved using the Peano Axioms include Goodstein's theorem.

With all these definitions, it is convenient to include 0 (corresponding to the empty set) as a natural number. Including 0 is now the common convention among set theorists and logicians. Other mathematicians also include 0, and computer languages often start from zero when enumerating items like loop counters and string- or array-elements. On the other hand, many mathematicians have kept the older tradition to take 1 to be the first natural number.

Notation

The set of all natural numbers is standardly denoted N or ${\displaystyle \mathbb{N}.}$ Older texts have occasionally employed J as the symbol for this set.

Since natural numbers may contain 0 or not, it may be important to know which version is referred to. This is often specified by the context, but may also be done by using a subscript or a superscript in the notation, such as:

• Naturals without zero: ${\displaystyle \{1,2,...\}={\mathbb{N}}^{\ast }={\mathbb{N}}^{+}={\mathbb{N}}_0\setminus \{0\}={\mathbb{N}}_1}$
• Naturals with zero: ${\displaystyle \{0,1,2,...\}={\mathbb{N}}_0={\mathbb{N}}^0={\mathbb{N}}^{\ast }\cup \{0\}}$

Alternatively, since the natural numbers naturally form a subset of the integers (often denoted ${\displaystyle \mathbb{Z}}$), they may be referred to as the positive, or the non-negative integers, respectively. To be unambiguous about whether 0 is included or not, sometimes a superscript "${\displaystyle \ast }$" or "+" is added in the former case, and a subscript (or superscript) "0" is added in the latter case:

${\displaystyle \{1,2,3,\dots \}=\{x\in \mathbb{Z}:x>0\}={\mathbb{Z}}^{+}={\mathbb{Z}}_{>0}}$

${\displaystyle \{0,1,2,\dots \}=\{x\in \mathbb{Z}:x\ge 0\}={\mathbb{Z}}_0^{+}={\mathbb{Z}}_{\ge 0}}$

Properties

This section uses the convention ${\displaystyle \mathbb{N}={\mathbb{N}}_0={\mathbb{N}}^{\ast }\cup \{0\}}$.

Addition

Given the set ${\displaystyle \mathbb{N}}$ of natural numbers and the successor function ${\displaystyle S:\mathbb{N}\to \mathbb{N}}$ sending each natural number to the next one, one can define addition of natural numbers recursively by setting a + 0 = a and a + S(b) = S(a + b) for all a, b. Thus, a + 1 = a + S(0) = S(a+0) = S(a), a + 2 = a + S(1) = S(a+1) = S(S(a)), and so on. The algebraic structure ${\displaystyle (\mathbb{N},+)}$ is a commutative monoid with identity element 0. It is a free monoid on one generator. This commutative monoid satisfies the cancellation property, so it can be embedded in a group. The smallest group containing the natural numbers is the integers.

If 1 is defined as S(0), then b + 1 = b + S(0) = S(b + 0) = S(b). That is, b + 1 is simply the successor of b.

Multiplication

Analogously, given that addition has been defined, a multiplication operator ${\displaystyle \times }$ can be defined via a × 0 = 0 and a × S(b) = (a × b) + a. This turns ${\displaystyle ({\mathbb{N}}^{\ast },\times )}$ into a free commutative monoid with identity element 1; a generator set for this monoid is the set of prime numbers.

Relationship between addition and multiplication

Addition and multiplication are compatible, which is expressed in the distribution law: a × (b + c) = (a × b) + (a × c). These properties of addition and multiplication make the natural numbers an instance of a commutative semiring. Semirings are an algebraic generalization of the natural numbers where multiplication is not necessarily commutative. The lack of additive inverses, which is equivalent to the fact that ${\displaystyle \mathbb{N}}$ is not closed under subtraction (that is, subtracting one natural from another does not always result in another natural), means that ${\displaystyle \mathbb{N}}$ is not a ring; instead it is a semiring (also known as a rig).

If the natural numbers are taken as "excluding 0", and "starting at 1", the definitions of + and × are as above, except that they begin with a + 1 = S(a) and a × 1 = a. Furthermore, ${\displaystyle ({\mathbb{N}}^{\mathbb{\ast }},+)}$ has no identity element.

Order

In this section, juxtaposed variables such as ab indicate the product a × b, and the standard order of operations is assumed.

A total order on the natural numbers is defined by letting a ≤ b if and only if there exists another natural number c where a + c = b. This order is compatible with the arithmetical operations in the following sense: if a, b and c are natural numbers and a ≤ b, then a + c ≤ b + c and ac ≤ bc.

An important property of the natural numbers is that they are well-ordered: every non-empty set of natural numbers has a least element. The rank among well-ordered sets is expressed by an ordinal number; for the natural numbers, this is denoted as ω (omega).

Division

In this section, juxtaposed variables such as ab indicate the product a × b, and the standard order of operations is assumed.

While it is in general not possible to divide one natural number by another and get a natural number as result, the procedure of division with remainder or Euclidean division is available as a substitute: for any two natural numbers a and b with b ≠ 0 there are natural numbers q and r such that

${\displaystyle a=bq+r\text{ and }r<b.}$

The number q is called the quotient and r is called the remainder of the division of a by b. The numbers q and r are uniquely determined by a and b. This Euclidean division is key to the several other properties (divisibility), algorithms (such as the Euclidean algorithm), and ideas in number theory.

Algebraic properties satisfied by the natural numbers

The addition (+) and multiplication (×) operations on natural numbers as defined above have several algebraic properties:

• Closure under addition and multiplication: for all natural numbers a and b, both a + b and a × b are natural numbers.
• Associativity: for all natural numbers a, b, and c, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.
• Commutativity: for all natural numbers a and b, a + b = b + a and a × b = b × a.
• Existence of identity elements: for every natural number a, a + 0 = a and a × 1 = a.
  • If the natural numbers are taken as "excluding 0", and "starting at 1", then for every natural number a, a × 1 = a. However, the "existence of additive identity element" property is not satisfied
• Distributivity of multiplication over addition for all natural numbers a, b, and c, a × (b + c) = (a × b) + (a × c).
• No nonzero zero divisors: if a and b are natural numbers such that a × b = 0, then a = 0 or b = 0 (or both).
  • If the natural numbers are taken as "excluding 0", and "starting at 1", the "no nonzero zero divisors" property is not satisfied.

Generalizations

Two important generalizations of natural numbers arise from the two uses of counting and ordering: cardinal numbers and ordinal numbers.

• A natural number can be used to express the size of a finite set; more precisely, a cardinal number is a measure for the size of a set, which is even suitable for infinite sets. This concept of "size" relies on maps between sets, such that two sets have the same size, exactly if there exists a bijection between them. The set of natural numbers itself, and any bijective image of it, is said to be countably infinite and to have cardinality aleph-null (ℵ₀).
• Natural numbers are also used as linguistic ordinal numbers: "first", "second", "third", and so forth. This way they can be assigned to the elements of a totally ordered finite set, and also to the elements of any well-ordered countably infinite set. This assignment can be generalized to general well-orderings with a cardinality beyond countability, to yield the ordinal numbers. An ordinal number may also be used to describe the notion of "size" for a well-ordered set, in a sense different from cardinality: if there is an order isomorphism (more than a bijection) between two well-ordered sets, they have the same ordinal number. The first ordinal number that is not a natural number is expressed as ω; this is also the ordinal number of the set of natural numbers itself.

The least ordinal of cardinality ℵ₀ (that is, the initial ordinal of ℵ₀) is ω but many well-ordered sets with cardinal number ℵ₀ have an ordinal number greater than ω.

For finite well-ordered sets, there is a one-to-one correspondence between ordinal and cardinal numbers; therefore they can both be expressed by the same natural number, the number of elements of the set. This number can also be used to describe the position of an element in a larger finite, or an infinite, sequence.

A countable non-standard model of arithmetic satisfying the Peano Arithmetic (that is, the first-order Peano axioms) was developed by Skolem in 1933. The hypernatural numbers are an uncountable model that can be constructed from the ordinary natural numbers via the ultrapower construction.

Georges Reeb used to claim provocatively that "The naïve integers don't fill up" ${\displaystyle \mathbb{N}}$. Other generalizations are discussed in the article on numbers.

Formal definitions

There are two standard methods for formally defining natural numbers. The first one, named for Giuseppe Peano, consists of an autonomous axiomatic theory called Peano arithmetic, based on few axioms called Peano axioms.

The second definition is based on set theory. It defines the natural numbers as specific sets. More precisely, each natural number n is defined as an explicitly defined set, whose elements allow counting the elements of other sets, in the sense that the sentence "a set S has n elements" means that there exists a one to one correspondence between the two sets n and S.

The sets used to define natural numbers satisfy Peano axioms. It follows that every theorem that can be stated and proved in Peano arithmetic can also be proved in set theory. However, the two definitions are not equivalent, as there are theorems that can be stated in terms of Peano arithmetic and proved in set theory, which are not provable inside Peano arithmetic. A probable example is Fermat's Last Theorem.

The definition of the integers as sets satisfying Peano axioms provide a model of Peano arithmetic inside set theory. An important consequence is that, if set theory is consistent (as it is usually guessed), then Peano arithmetic is consistent. In other words, if a contradiction could be proved in Peano arithmetic, then set theory would be contradictory, and every theorem of set theory would be both true and wrong.

Peano axioms

Main article: Peano axioms

The five Peano axioms are the following:

1. 0 is a natural number.
2. Every natural number has a successor which is also a natural number.
3. 0 is not the successor of any natural number.
4. If the successor of ${\displaystyle x}$ equals the successor of ${\displaystyle y}$, then ${\displaystyle x}$ equals ${\displaystyle y}$.
5. The axiom of induction: If a statement is true of 0, and if the truth of that statement for a number implies its truth for the successor of that number, then the statement is true for every natural number.

These are not the original axioms published by Peano, but are named in his honor. Some forms of the Peano axioms have 1 in place of 0. In ordinary arithmetic, the successor of ${\displaystyle x}$ is ${\displaystyle x+1}$.

Set-theoretic definition

Main article: Set-theoretic definition of natural numbers

Intuitively, the natural number n is the common property of all sets that have n elements. So, it seems natural to define n as an equivalence class under the relation "can be made in one to one correspondence". Unfortunately, this does not work in set theory, as such an equivalence class would not be a set (because of Russell's paradox). The standard solution is to define a particular set with n elements that will be called the natural number n.

The following definition was first published by John von Neumann, although Levy attributes the idea to unpublished work of Zermelo in 1916. As this definition extends to infinite set as a definition of ordinal number, the sets considered below are sometimes called von Neumann ordinals.

The definition proceeds as follows:

• Call 0 = { }, the empty set.
• Define the successor S(a) of any set a by S(a) = a ∪ {a}.
• By the axiom of infinity, there exist sets which contain 0 and are closed under the successor function. Such sets are said to be inductive. The intersection of all inductive sets is still an inductive set.
• This intersection is the set of the natural numbers.

It follows that the natural numbers are defined iteratively as follows:

• 0 = { },
• 1 = 0 ∪ {0} = {0} = {{ }},
• 2 = 1 ∪ {1} = {0, 1} = {{ }, {{ }}},
• 3 = 2 ∪ {2} = {0, 1, 2} = {{ }, {{ }}, {{ }, {{ }}}},
• n = n−1 ∪ {n−1} = {0, 1, ..., n−1} = {{ }, {{ }}, ..., {{ }, {{ }}, ...}},
• etc.

It can be checked that the natural numbers satisfies the Peano axioms.

With this definition, given a natural number n, the sentence "a set S has n elements" can be formally defined as "there exists a bijection from n to S. This formalizes the operation of counting the elements of S. Also, n ≤ m if and only if n is a subset of m. In other words, the set inclusion defines the usual total order on the natural numbers. This order is a well-order.

It follows from the definition that each natural number is equal to the set of all natural numbers less than it. This definition, can be extended to the von Neumann definition of ordinals for defining all ordinal numbers, including the infinite ones: "each ordinal is the well-ordered set of all smaller ordinals."

If one does not accept the axiom of infinity, the natural numbers may not form a set. Nevertheless, the natural numbers can still be individually defined as above, and they still satisfy the Peano axioms.

There are other set theoretical constructions. In particular, Ernst Zermelo provided a construction that is nowadays only of historical interest, and is sometimes referred to as Zermelo ordinals. It consists in defining 0 as the empty set, and S(a) = {a}.

With this definition each natural number is a singleton set. So, the property of the natural numbers to represent cardinalities is not directly accessible; only the ordinal property (being the nth element of a sequence) is immediate. Unlike von Neumann's construction, the Zermelo ordinals do not extend to infinite ordinals.