Proton–proton chain

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Proton%E2%80%93proton_chain

Logarithm of the relative energy output (ε) of proton–proton (PP), CNO and Triple-α fusion processes at different temperatures (T). The dashed line shows the combined energy generation of the PP and CNO processes within a star. At the Sun's core temperature of 15.5 million K the PP process is dominant. The PP process and the CNO process are equal at around 20 MK.

Scheme of the proton–proton branch I reaction

The proton–proton chain, also commonly referred to as the p–p chain, is one of two known sets of nuclear fusion reactions by which stars convert hydrogen to helium. It dominates in stars with masses less than or equal to that of the Sun, whereas the CNO cycle, the other known reaction, is suggested by theoretical models to dominate in stars with masses greater than about 1.3 times that of the Sun.

In general, proton–proton fusion can occur only if the kinetic energy (temperature) of the protons is high enough to overcome their mutual electrostatic repulsion.

In the Sun, deuteron-producing events are rare. Diprotons are the much more common result of proton–proton reactions within the star, and diprotons almost immediately decay back into two protons. Since the conversion of hydrogen to helium is slow, the complete conversion of the hydrogen initially in the core of the Sun is calculated to take more than ten billion years.

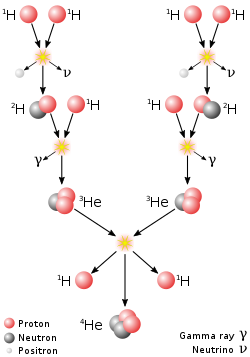
Although sometimes called the "proton–proton chain reaction", it is not a chain reaction in the normal sense. In most nuclear reactions, a chain reaction designates a reaction that produces a product, such as neutrons given off during fission, that quickly induces another such reaction. The proton–proton chain is, like a decay chain, a series of reactions. The product of one reaction is the starting material of the next reaction. There are two main chains leading from hydrogen to helium in the Sun. One chain has five reactions, the other chain has six.

History of the theory

The theory that proton–proton reactions are the basic principle by which the Sun and other stars burn was advocated by Arthur Eddington in the 1920s. At the time, the temperature of the Sun was considered to be too low to overcome the Coulomb barrier. After the development of quantum mechanics, it was discovered that tunneling of the wavefunctions of the protons through the repulsive barrier allows for fusion at a lower temperature than the classical prediction.

In 1939, Hans Bethe attempted to calculate the rates of various reactions in stars. Starting with two protons combining to give a deuterium nucleus and a positron he found what we now call Branch II of the proton–proton chain. But he did not consider the reaction of two ³
He nuclei (Branch I) which we now know to be important. This was part of the body of work in stellar nucleosynthesis for which Bethe won the Nobel Prize in Physics in 1967.

The proton–proton chain

The first step in all the branches is the fusion of two protons into a deuteron. As the protons fuse, one of them undergoes beta plus decay, converting into a neutron by emitting a positron and an electron neutrino (though a small amount of deuterium nuclei is produced by the "pep" reaction, see below):

p

+

p

→

2 1D

+

e+

+

ν e

+

0.42 MeV

The positron will annihilate with an electron from the environment into two gamma rays. Including this annihilation and the energy of the neutrino, the net reaction

p

+

p

+ e− → 2 1D

+

ν e

+

1.442 MeV

(which is the same as the PEP reaction, see below) has a Q value (released energy) of 1.442 MeV: The relative amounts of energy going to the neutrino and to the other products is variable.

This is the rate-limiting reaction and is extremely slow due to it being initiated by the weak nuclear force. The average proton in the core of the Sun waits 9 billion years before it successfully fuses with another proton. It has not been possible to measure the cross-section of this reaction experimentally because it is so low but it can be calculated from theory.

After it is formed, the deuteron produced in the first stage can fuse with another proton to produce the stable, light isotope of helium, ³
He
:

2 1D

+

1 1H

→

3 2He

+

γ

+

5.493 MeV

This process, mediated by the strong nuclear force rather than the weak force, is extremely fast by comparison to the first step. It is estimated that, under the conditions in the Sun's core, each newly created deuterium nucleus exists for only about one second before it is converted into helium-3.

In the Sun, each helium-3 nucleus produced in these reactions exists for only about 400 years before it is converted into helium-4. Once the helium-3 has been produced, there are four possible paths to generate ⁴
He
. In p–p I, helium-4 is produced by fusing two helium-3 nuclei; the p–p II and p–p III branches fuse ³
He
with pre-existing ⁴
He
to form beryllium-7, which undergoes further reactions to produce two helium-4 nuclei.

About 99% of the energy output of the sun comes from the various p–p chains, with the other 1% coming from the CNO cycle. According to one model of the sun, 83.3 percent of the ⁴
He
produced by the various p–p branches is produced via branch I while p–p II produces 16.68 percent and p–p III 0.02 percent. Since half the neutrinos produced in branches II and III are produced in the first step (synthesis of a deuteron), only about 8.35 percent of neutrinos come from the later steps (see below), and about 91.65 percent are from deuteron synthesis. However, another solar model from around the same time gives only 7.14 percent of neutrinos from the later steps and 92.86 percent from the synthesis of deuterium nuclei. The difference is apparently due to slightly different assumptions about the composition and metallicity of the sun.

There is also the extremely rare p–p IV branch. Other even rarer reactions may occur. The rate of these reactions is very low due to very small cross-sections, or because the number of reacting particles is so low that any reactions that might happen are statistically insignificant.

The overall reaction is:

4 ¹H⁺ + 2 e^- → ⁴He²⁺ + 2 ν_e

releasing 26.73 MeV of energy, some of which is lost to the neutrinos.

The p–p I branch

3 2He

+

3 2He

→

4 2He

+

2 1 1H

+

12.859 MeV

The complete chain releases a net energy of 26.732 MeV but 2.2 percent of this energy (0.59 MeV) is lost to the neutrinos that are produced. The p–p I branch is dominant at temperatures of 10 to 18 MK. Below 10 MK, the p–p chain proceeds at slow rate, resulting in a low production of ⁴
He
.

The p–p II branch

Proton–proton II chain

See also: Lithium burning

3 2He	+	4 2He	→	7 4Be	+	γ	+	1.59 MeV
7 4Be	+	e−	→	7 3Li	+	ν e	+	0.861 MeV	/	0.383 MeV
7 3Li	+	1 1H	→	24 2He			+	17.35 MeV

The p–p II branch is dominant at temperatures of 18 to 25 MK.

Note that the energies in the second reaction above are the energies of the neutrinos that are produced by the reaction. 90 percent of the neutrinos produced in the reaction of ⁷
Be
to ⁷
Li
carry an energy of 0.861 MeV, while the remaining 10 percent carry 0.383 MeV. The difference is whether the lithium-7 produced is in the ground state or an excited (metastable) state, respectively. The total energy released going from ⁷
Be to stable ⁷
Li is about 0.862 MeV, almost all of which is lost to the neutrino if the decay goes directly to the stable lithium.

The p–p III branch

Proton–proton III chain

3 2He	+	4 2He	→	7 4Be	+	γ			+	1.59 MeV
7 4Be	+	1 1H	→	8 5B	+	γ
8 5B			→	8 4Be	+	e+	+	ν e
8 4Be			→	2 4 2He

The last three stages of this chain, plus the positron annihilation, contribute a total of 18.209 MeV, though much of this is lost to the neutrino.

The p–p III chain is dominant if the temperature exceeds 25 MK.

The p–p III chain is not a major source of energy in the Sun, but it was very important in the solar neutrino problem because it generates very high energy neutrinos (up to 14.06 MeV).

The p–p IV (Hep) branch

This reaction is predicted theoretically, but it has never been observed due to its rarity (about 0.3 ppm in the Sun). In this reaction, helium-3 captures a proton directly to give helium-4, with an even higher possible neutrino energy (up to 18.8 MeV).

3 2He

+

1 1H

→

4 2He

+

e+

+

ν e

The mass–energy relationship gives 19.795 MeV for the energy released by this reaction plus the ensuing annihilation, some of which is lost to the neutrino.

Energy release

Comparing the mass of the final helium-4 atom with the masses of the four protons reveals that 0.7 percent of the mass of the original protons has been lost. This mass has been converted into energy, in the form of kinetic energy of produced particles, gamma rays, and neutrinos released during each of the individual reactions. The total energy yield of one whole chain is 26.73 MeV.

Energy released as gamma rays will interact with electrons and protons and heat the interior of the Sun. Also kinetic energy of fusion products (e.g. of the two protons and the ⁴
₂He
from the p–p I reaction) adds energy to the plasma in the Sun. This heating keeps the core of the Sun hot and prevents it from collapsing under its own weight as it would if the sun were to cool down.

Neutrinos do not interact significantly with matter and therefore do not heat the interior and thereby help support the Sun against gravitational collapse. Their energy is lost: the neutrinos in the p–p I, p–p II, and p–p III chains carry away 2.0%, 4.0%, and 28.3% of the energy in those reactions, respectively.

The following table calculates the amount of energy lost to neutrinos and the amount of "solar luminosity" coming from the three branches. "Luminosity" here means the amount of energy given off by the Sun as electromagnetic radiation rather than as neutrinos. The starting figures used are the ones mentioned higher in this article. The table concerns only the 99% of the power and neutrinos that come from the p–p reactions, not the 1% coming from the CNO cycle.

Luminosity production in the sun

Branch	Percent of helium-4 produced	Percent loss due to neutrino production	Relative amount of energy lost	Relative amount of luminosity produced	Percentage of total luminosity
Branch I	83.3	2	1.67	81.6	83.6
Branch II	16.68	4	0.67	16.0	16.4
Branch III	0.02	28.3	0.0057	0.014	0.015
Total	100		2.34	97.7	100

The PEP reaction

Proton–proton and electron-capture reactions in a star

A deuteron can also be produced by the rare pep (proton–electron–proton) reaction (electron capture):

1 1H

+

e−

+

1 1H

→

2 1D+

+

ν e

In the Sun, the frequency ratio of the pep reaction versus the p–p reaction is 1:400. However, the neutrinos released by the pep reaction are far more energetic: while neutrinos produced in the first step of the p–p reaction range in energy up to 0.42 MeV, the pep reaction produces sharp-energy-line neutrinos of 1.44 MeV. Detection of solar neutrinos from this reaction were reported by the Borexino collaboration in 2012.

Both the pep and p–p reactions can be seen as two different Feynman representations of the same basic interaction, where the electron passes to the right side of the reaction as a positron. This is represented in the figure of proton–proton and electron-capture reactions in a star, available at the NDM'06 web site.

Standard solar model

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Standard_solar_model

The standard solar model (SSM) is a mathematical treatment of the Sun as a spherical ball of gas (in varying states of ionisation, with the hydrogen in the deep interior being a completely ionised plasma). This model, technically the spherically symmetric quasi-static model of a star, has stellar structure described by several differential equations derived from basic physical principles. The model is constrained by boundary conditions, namely the luminosity, radius, age and composition of the Sun, which are well determined. The age of the Sun cannot be measured directly; one way to estimate it is from the age of the oldest meteorites, and models of the evolution of the Solar System. The composition in the photosphere of the modern-day Sun, by mass, is 74.9% hydrogen and 23.8% helium. All heavier elements, called metals in astronomy, account for less than 2 percent of the mass. The SSM is used to test the validity of stellar evolution theory. In fact, the only way to determine the two free parameters of the stellar evolution model, the helium abundance and the mixing length parameter (used to model convection in the Sun), are to adjust the SSM to "fit" the observed Sun.

A calibrated solar model

A star is considered to be at zero age (protostellar) when it is assumed to have a homogeneous composition and to be just beginning to derive most of its luminosity from nuclear reactions (so neglecting the period of contraction from a cloud of gas and dust). To obtain the SSM, a one solar mass (M_☉) stellar model at zero age is evolved numerically to the age of the Sun. The abundance of elements in the zero age solar model is estimated from primordial meteorites. Along with this abundance information, a reasonable guess at the zero-age luminosity (such as the present-day Sun's luminosity) is then converted by an iterative procedure into the correct value for the model, and the temperature, pressure and density throughout the model calculated by solving the equations of stellar structure numerically assuming the star to be in a steady state. The model is then evolved numerically up to the age of the Sun. Any discrepancy from the measured values of the Sun's luminosity, surface abundances, etc. can then be used to refine the model. For example, since the Sun formed, some of the helium and heavy elements have settled out of the photosphere by diffusion. As a result, the Solar photosphere now contains about 87% as much helium and heavy elements as the protostellar photosphere had; the protostellar Solar photosphere was 71.1% hydrogen, 27.4% helium, and 1.5% metals. A measure of heavy-element settling by diffusion is required for a more accurate model.

Numerical modelling of the stellar structure equations

Main article: Stellar structure

The differential equations of stellar structure, such as the equation of hydrostatic equilibrium, are integrated numerically. The differential equations are approximated by difference equations. The star is imagined to be made up of spherically symmetric shells and the numerical integration carried out in finite steps making use of the equations of state, giving relationships for the pressure, the opacity and the energy generation rate in terms of the density, temperature and composition.

Evolution of the Sun

Main article: Stellar evolution

Nuclear reactions in the core of the Sun change its composition, by converting hydrogen nuclei into helium nuclei by the proton–proton chain and (to a lesser extent in the Sun than in more massive stars) the CNO cycle. This increases the mean molecular weight in the core of the Sun, which should lead to a decrease in pressure. This does not happen as instead the core contracts. By the virial theorem half of the gravitational potential energy released by this contraction goes towards raising the temperature of the core, and the other half is radiated away. This increase in temperature also increases the pressure and restores the balance of hydrostatic equilibrium. The luminosity of the Sun is increased by the temperature rise, increasing the rate of nuclear reactions. The outer layers expand to compensate for the increased temperature and pressure gradients, so the radius also increases.

No star is completely static, but stars stay on the main sequence (burning hydrogen in the core) for long periods. In the case of the Sun, it has been on the main sequence for roughly 4.6 billion years, and will become a red giant in roughly 6.5 billion years for a total main sequence lifetime of roughly 11 billion (10¹⁰) years. Thus the assumption of steady state is a very good approximation. For simplicity, the stellar structure equations are written without explicit time dependence, with the exception of the luminosity gradient equation:

$${\displaystyle \frac{dL}{dr}=4\pi r^2\rho \left(\epsilon -{\epsilon }_{\nu }\right)}$$

Here L is the luminosity, ε is the nuclear energy generation rate per unit mass and ε_ν is the luminosity due to neutrino emission (see below for the other quantities). The slow evolution of the Sun on the main sequence is then determined by the change in the nuclear species (principally hydrogen being consumed and helium being produced). The rates of the various nuclear reactions are estimated from particle physics experiments at high energies, which are extrapolated back to the lower energies of stellar interiors (the Sun burns hydrogen rather slowly). Historically, errors in the nuclear reaction rates have been one of the biggest sources of error in stellar modelling. Computers are employed to calculate the varying abundances (usually by mass fraction) of the nuclear species. A particular species will have a rate of production and a rate of destruction, so both are needed to calculate its abundance over time, at varying conditions of temperature and density. Since there are many nuclear species, a computerised reaction network is needed to keep track of how all the abundances vary together.

According to the Vogt–Russell theorem, the mass and the composition structure throughout a star uniquely determine its radius, luminosity, and internal structure, as well as its subsequent evolution (though this "theorem" was only intended to apply to the slow, stable phases of stellar evolution and certainly does not apply to the transitions between stages and rapid evolutionary stages). The information about the varying abundances of nuclear species over time, along with the equations of state, is sufficient for a numerical solution by taking sufficiently small time increments and using iteration to find the unique internal structure of the star at each stage.

Purpose of the standard solar model

The SSM serves two purposes:

• it provides estimates for the helium abundance and mixing length parameter by forcing the stellar model to have the correct luminosity and radius at the Sun's age,
• it provides a way to evaluate more complex models with additional physics, such as rotation, magnetic fields and diffusion or improvements to the treatment of convection, such as modelling turbulence, and convective overshooting.

Like the Standard Model of particle physics and the standard cosmology model the SSM changes over time in response to relevant new theoretical or experimental physics discoveries.

Energy transport in the Sun

As described in the Sun article, the Sun has a radiative core and a convective outer envelope. In the core, the luminosity due to nuclear reactions is transmitted to outer layers principally by radiation. However, in the outer layers the temperature gradient is so great that radiation cannot transport enough energy. As a result, thermal convection occurs as thermal columns carry hot material to the surface (photosphere) of the Sun. Once the material cools off at the surface, it plunges back downward to the base of the convection zone, to receive more heat from the top of the radiative zone.

In a solar model, as described in stellar structure, one considers the density ${\displaystyle \rho (r)}$, temperature T(r), total pressure (matter plus radiation) P(r), luminosity l(r) and energy generation rate per unit mass ε(r) in a spherical shell of a thickness dr at a distance r from the center of the star.

Radiative transport of energy is described by the radiative temperature gradient equation:

$${\displaystyle \frac{dT}{dr}=-\frac{3\kappa \rho l}{16\pi r^2\sigma T^3},}$$

where κ is the opacity of the matter, σ is the Stefan–Boltzmann constant, and the Boltzmann constant is set to one.

Convection is described using mixing length theory and the corresponding temperature gradient equation (for adiabatic convection) is:

$${\displaystyle \frac{dT}{dr}=\left(1-\frac{1}{\gamma }\right)\frac{T}{P}\frac{dP}{dr},}$$

where γ = c_p / c_v is the adiabatic index, the ratio of specific heats in the gas. (For a fully ionized ideal gas, γ = 5/3.)

Near the base of the Sun's convection zone, the convection is adiabatic, but near the surface of the Sun, convection is not adiabatic.

Simulations of near-surface convection

A more realistic description of the uppermost part of the convection zone is possible through detailed three-dimensional and time-dependent hydrodynamical simulations, taking into account radiative transfer in the atmosphere. Such simulations successfully reproduce the observed surface structure of solar granulation, as well as detailed profiles of lines in the solar radiative spectrum, without the use of parametrized models of turbulence. The simulations only cover a very small fraction of the solar radius, and are evidently far too time-consuming to be included in general solar modeling. Extrapolation of an averaged simulation through the adiabatic part of the convection zone by means of a model based on the mixing-length description, demonstrated that the adiabat predicted by the simulation was essentially consistent with the depth of the solar convection zone as determined from helioseismology. An extension of mixing-length theory, including effects of turbulent pressure and kinetic energy, based on numerical simulations of near-surface convection, has been developed.

This section is adapted from the Christensen-Dalsgaard review of helioseismology, Chapter IV.

Equations of state

The numerical solution of the differential equations of stellar structure requires equations of state for the pressure, opacity and energy generation rate, as described in stellar structure, which relate these variables to the density, temperature and composition.

Helioseismology

Main article: Helioseismology

Helioseismology is the study of the wave oscillations in the Sun. Changes in the propagation of these waves through the Sun reveal inner structures and allow astrophysicists to develop extremely detailed profiles of the interior conditions of the Sun. In particular, the location of the convection zone in the outer layers of the Sun can be measured, and information about the core of the Sun provides a method, using the SSM, to calculate the age of the Sun, independently of the method of inferring the age of the Sun from that of the oldest meteorites. This is another example of how the SSM can be refined.

Neutrino production

Hydrogen is fused into helium through several different interactions in the Sun. The vast majority of neutrinos are produced through the pp chain, a process in which four protons are combined to produce two protons, two neutrons, two positrons, and two electron neutrinos. Neutrinos are also produced by the CNO cycle, but that process is considerably less important in the Sun than in other stars.

Most of the neutrinos produced in the Sun come from the first step of the pp chain but their energy is so low (<0.425 MeV) they are very difficult to detect. A rare side branch of the pp chain produces the "boron-8" neutrinos with a maximum energy of roughly 15 MeV, and these are the easiest neutrinos to detect. A very rare interaction in the pp chain produces the "hep" neutrinos, the highest energy neutrinos predicted to be produced by the Sun. They are predicted to have a maximum energy of about 18 MeV.

All of the interactions described above produce neutrinos with a spectrum of energies. The electron capture of ⁷Be produces neutrinos at either roughly 0.862 MeV (~90%) or 0.384 MeV (~10%).

Neutrino detection

The weakness of the neutrino's interactions with other particles means that most neutrinos produced in the core of the Sun can pass all the way through the Sun without being absorbed. It is possible, therefore, to observe the core of the Sun directly by detecting these neutrinos.

History

Main article: solar neutrino problem

The first experiment to successfully detect cosmic neutrinos was Ray Davis's chlorine experiment, in which neutrinos were detected by observing the conversion of chlorine nuclei to radioactive argon in a large tank of perchloroethylene. This was a reaction channel expected for neutrinos, but since only the number of argon decays was counted, it did not give any directional information, such as where the neutrinos came from. The experiment found about 1/3 as many neutrinos as were predicted by the standard solar model of the time, and this problem became known as the solar neutrino problem.

While it is now known that the chlorine experiment detected neutrinos, some physicists at the time were suspicious of the experiment, mainly because they did not trust such radiochemical techniques. Unambiguous detection of solar neutrinos was provided by the Kamiokande-II experiment, a water Cherenkov detector with a low enough energy threshold to detect neutrinos through neutrino-electron elastic scattering. In the elastic scattering interaction the electrons coming out of the point of reaction strongly point in the direction that the neutrino was travelling, away from the Sun. This ability to "point back" at the Sun was the first conclusive evidence that the Sun is powered by nuclear interactions in the core. While the neutrinos observed in Kamiokande-II were clearly from the Sun, the rate of neutrino interactions was again suppressed compared to theory at the time. Even worse, the Kamiokande-II experiment measured about 1/2 the predicted flux, rather than the chlorine experiment's 1/3.

The solution to the solar neutrino problem was finally experimentally determined by the Sudbury Neutrino Observatory (SNO). The radiochemical experiments were only sensitive to electron neutrinos, and the signal in the water Cerenkov experiments was dominated by the electron neutrino signal. The SNO experiment, by contrast, had sensitivity to all three neutrino flavours. By simultaneously measuring the electron neutrino and total neutrino fluxes the experiment demonstrated that the suppression was due to the MSW effect, the conversion of electron neutrinos from their pure flavour state into the second neutrino mass eigenstate as they passed through a resonance due to the changing density of the Sun. The resonance is energy dependent, and "turns on" near 2MeV. The water Cerenkov detectors only detect neutrinos above about 5MeV, while the radiochemical experiments were sensitive to lower energy (0.8MeV for chlorine, 0.2MeV for gallium), and this turned out to be the source of the difference in the observed neutrino rates at the two types of experiments.

Proton–proton chain

All neutrinos from the proton–proton chain reaction (PP neutrinos) have been detected except hep neutrinos (next point). Three techniques have been adopted: The radiochemical technique, used by Homestake, GALLEX, GNO and SAGE allowed to measure the neutrino flux above a minimum energy. The detector SNO used scattering on deuterium that allowed to measure the energy of the events, thereby identifying the single components of the predicted SSM neutrino emission. Finally, Kamiokande, Super-Kamiokande, SNO, Borexino and KamLAND used elastic scattering on electrons, which allows the measurement of the neutrino energy. Boron8 neutrinos have been seen by Kamiokande, Super-Kamiokande, SNO, Borexino, KamLAND. Beryllium7, pep, and PP neutrinos have been seen only by Borexino to date.

HEP neutrinos

The highest energy neutrinos have not yet been observed due to their small flux compared to the boron-8 neutrinos, so thus far only limits have been placed on the flux. No experiment yet has had enough sensitivity to observe the flux predicted by the SSM.

CNO cycle

Neutrinos from the CNO cycle of solar energy generation – i.e., the CNO-neutrinos – are also expected to provide observable events below 1 MeV. They have not yet been observed due to experimental noise (background). Ultra-pure scintillator detectors have the potential to probe the flux predicted by the SSM. This detection could be possible already in Borexino; the next scientific occasions will be in SNO+ and, on the longer term, in LENA and JUNO, three detectors that will be larger but will use the same principles of Borexino. The Borexino Collaboration has confirmed that the CNO cycle accounts for 1% of the energy generation within the Sun's core.

Future experiments

While radiochemical experiments have in some sense observed the pp and Be7 neutrinos they have measured only integral fluxes. The "holy grail" of solar neutrino experiments would detect the Be7 neutrinos with a detector that is sensitive to the individual neutrino energies. This experiment would test the MSW hypothesis by searching for the turn-on of the MSW effect. Some exotic models are still capable of explaining the solar neutrino deficit, so the observation of the MSW turn on would, in effect, finally solve the solar neutrino problem.

Core temperature prediction

The flux of boron-8 neutrinos is highly sensitive to the temperature of the core of the Sun, ${\displaystyle \varphi ({}^8\text{B})\propto T^{25}}$. For this reason, a precise measurement of the boron-8 neutrino flux can be used in the framework of the standard solar model as a measurement of the temperature of the core of the Sun. This estimate was performed by Fiorentini and Ricci after the first SNO results were published, and they obtained a temperature of ${\displaystyle T_{\text{sun}}=15.7\times {10}^6\text{K}\pm 1\mathrm{\%}}$ from a determined neutrino flux of 5.2×10⁶/cm²·s.

Lithium depletion at the solar surface

Stellar models of the Sun's evolution predict the solar surface chemical abundance pretty well except for lithium (Li). The surface abundance of Li on the Sun is 140 times less than the protosolar value (i.e. the primordial abundance at the Sun's birth), yet the temperature at the base of the surface convective zone is not hot enough to burn – and hence deplete – Li. This is known as the solar lithium problem. A large range of Li abundances is observed in solar-type stars of the same age, mass, and metallicity as the Sun. Observations of an unbiased sample of stars of this type with or without observed planets (exoplanets) showed that the known planet-bearing stars have less than one per cent of the primordial Li abundance, and of the remainder half had ten times as much Li. It is hypothesised that the presence of planets may increase the amount of mixing and deepen the convective zone to such an extent that the Li can be burned. A possible mechanism for this is the idea that the planets affect the angular momentum evolution of the star, thus changing the rotation of the star relative to similar stars without planets; in the case of the Sun slowing its rotation. More research is needed to discover where and when the fault in the modelling lies. Given the precision of helioseismic probes of the interior of the modern-day Sun, it is likely that the modelling of the protostellar Sun needs to be adjusted.

Stellar structure

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Stellar_structure 

Cross-section of the Sun

Stellar structure models describe the internal structure of a star in detail and make predictions about the luminosity, the color and the future evolution of the star. Different classes and ages of stars have different internal structures, reflecting their elemental makeup and energy transport mechanisms.

Energy transport

The different transport mechanisms of high-mass, intermediate-mass and low-mass stars

Different layers of the stars transport heat up and outwards in different ways, primarily convection and radiative transfer, but thermal conduction is important in white dwarfs.

Convection is the dominant mode of energy transport when the temperature gradient is steep enough so that a given parcel of gas within the star will continue to rise if it rises slightly via an adiabatic process. In this case, the rising parcel is buoyant and continues to rise if it is warmer than the surrounding gas; if the rising parcel is cooler than the surrounding gas, it will fall back to its original height. In regions with a low temperature gradient and a low enough opacity to allow energy transport via radiation, radiation is the dominant mode of energy transport.

The internal structure of a main sequence star depends upon the mass of the star.

In stars with masses of 0.3–1.5 solar masses (M_☉), including the Sun, hydrogen-to-helium fusion occurs primarily via proton–proton chains, which do not establish a steep temperature gradient. Thus, radiation dominates in the inner portion of solar mass stars. The outer portion of solar mass stars is cool enough that hydrogen is neutral and thus opaque to ultraviolet photons, so convection dominates. Therefore, solar mass stars have radiative cores with convective envelopes in the outer portion of the star.

In massive stars (greater than about 1.5 M_☉), the core temperature is above about 1.8×10⁷ K, so hydrogen-to-helium fusion occurs primarily via the CNO cycle. In the CNO cycle, the energy generation rate scales as the temperature to the 15th power, whereas the rate scales as the temperature to the 4th power in the proton-proton chains. Due to the strong temperature sensitivity of the CNO cycle, the temperature gradient in the inner portion of the star is steep enough to make the core convective. In the outer portion of the star, the temperature gradient is shallower but the temperature is high enough that the hydrogen is nearly fully ionized, so the star remains transparent to ultraviolet radiation. Thus, massive stars have a radiative envelope.

The lowest mass main sequence stars have no radiation zone; the dominant energy transport mechanism throughout the star is convection.

Equations of stellar structure

See also: Mass–luminosity relation and Polytrope

 

Temperature profile in the Sun

Mass inside a given radius in the Sun

Density profile in the Sun

 

Pressure profile in the Sun

The simplest commonly used model of stellar structure is the spherically symmetric quasi-static model, which assumes that a star is in a steady state and that it is spherically symmetric. It contains four basic first-order differential equations: two represent how matter and pressure vary with radius; two represent how temperature and luminosity vary with radius.

In forming the stellar structure equations (exploiting the assumed spherical symmetry), one considers the matter density ${\displaystyle \rho (r)}$, temperature ${\displaystyle T(r)}$, total pressure (matter plus radiation) ${\displaystyle P(r)}$, luminosity ${\displaystyle l(r)}$, and energy generation rate per unit mass ${\displaystyle ϵ(r)}$ in a spherical shell of a thickness ${\displaystyle \text{d}r}$ at a distance ${\displaystyle r}$ from the center of the star. The star is assumed to be in local thermodynamic equilibrium (LTE) so the temperature is identical for matter and photons. Although LTE does not strictly hold because the temperature a given shell "sees" below itself is always hotter than the temperature above, this approximation is normally excellent because the photon mean free path, ${\displaystyle \lambda }$, is much smaller than the length over which the temperature varies considerably, i. e. ${\displaystyle \lambda \ll T/|\mathrm{\nabla }T|}$.

First is a statement of hydrostatic equilibrium: the outward force due to the pressure gradient within the star is exactly balanced by the inward force due to gravity. This is sometimes referred to as stellar equilibrium.

${\displaystyle \frac{\text{d}P}{\text{d}r}=-\frac{Gm\rho }{r^2}}$,

where ${\displaystyle m(r)}$ is the cumulative mass inside the shell at ${\displaystyle r}$ and G is the gravitational constant. The cumulative mass increases with radius according to the mass continuity equation:

${\displaystyle \frac{\text{d}m}{\text{d}r}=4\pi r^2\rho .}$

Integrating the mass continuity equation from the star center (${\displaystyle r=0}$) to the radius of the star (${\displaystyle r=R}$) yields the total mass of the star.

Considering the energy leaving the spherical shell yields the energy equation:

${\displaystyle \frac{\text{d}l}{\text{d}r}=4\pi r^2\rho (ϵ-{ϵ}_{\nu })}$,

where ${\displaystyle {ϵ}_{\nu }}$ is the luminosity produced in the form of neutrinos (which usually escape the star without interacting with ordinary matter) per unit mass. Outside the core of the star, where nuclear reactions occur, no energy is generated, so the luminosity is constant.

The energy transport equation takes differing forms depending upon the mode of energy transport. For conductive energy transport (appropriate for a white dwarf), the energy equation is

${\displaystyle \frac{\text{d}T}{\text{d}r}=-\frac{1}{k}\frac{l}{4\pi r^2},}$

where k is the thermal conductivity.

In the case of radiative energy transport, appropriate for the inner portion of a solar mass main sequence star and the outer envelope of a massive main sequence star,

${\displaystyle \frac{\text{d}T}{\text{d}r}=-\frac{3\kappa \rho l}{64\pi r^2\sigma T^3},}$

where ${\displaystyle \kappa }$ is the opacity of the matter, ${\displaystyle \sigma }$ is the Stefan–Boltzmann constant, and the Boltzmann constant is set to one.

The case of convective energy transport does not have a known rigorous mathematical formulation, and involves turbulence in the gas. Convective energy transport is usually modeled using mixing length theory. This treats the gas in the star as containing discrete elements which roughly retain the temperature, density, and pressure of their surroundings but move through the star as far as a characteristic length, called the mixing length. For a monatomic ideal gas, when the convection is adiabatic, meaning that the convective gas bubbles don't exchange heat with their surroundings, mixing length theory yields

${\displaystyle \frac{\text{d}T}{\text{d}r}=\left(1-\frac{1}{\gamma }\right)\frac{T}{P}\frac{\text{d}P}{\text{d}r},}$

where ${\displaystyle \gamma =c_p/c_v}$ is the adiabatic index, the ratio of specific heats in the gas. (For a fully ionized ideal gas, ${\displaystyle \gamma =5/3}$.) When the convection is not adiabatic, the true temperature gradient is not given by this equation. For example, in the Sun the convection at the base of the convection zone, near the core, is adiabatic but that near the surface is not. The mixing length theory contains two free parameters which must be set to make the model fit observations, so it is a phenomenological theory rather than a rigorous mathematical formulation.

Also required are the equations of state, relating the pressure, opacity and energy generation rate to other local variables appropriate for the material, such as temperature, density, chemical composition, etc. Relevant equations of state for pressure may have to include the perfect gas law, radiation pressure, pressure due to degenerate electrons, etc. Opacity cannot be expressed exactly by a single formula. It is calculated for various compositions at specific densities and temperatures and presented in tabular form. Stellar structure codes (meaning computer programs calculating the model's variables) either interpolate in a density-temperature grid to obtain the opacity needed, or use a fitting function based on the tabulated values. A similar situation occurs for accurate calculations of the pressure equation of state. Finally, the nuclear energy generation rate is computed from nuclear physics experiments, using reaction networks to compute reaction rates for each individual reaction step and equilibrium abundances for each isotope in the gas.

Combined with a set of boundary conditions, a solution of these equations completely describes the behavior of the star. Typical boundary conditions set the values of the observable parameters appropriately at the surface (${\displaystyle r=R}$) and center (${\displaystyle r=0}$) of the star: ${\displaystyle P(R)=0}$, meaning the pressure at the surface of the star is zero; ${\displaystyle m(0)=0}$, there is no mass inside the center of the star, as required if the mass density remains finite; ${\displaystyle m(R)=M}$, the total mass of the star is the star's mass; and ${\displaystyle T(R)=T_{eff}}$, the temperature at the surface is the effective temperature of the star.

Although nowadays stellar evolution models describe the main features of color–magnitude diagrams, important improvements have to be made in order to remove uncertainties which are linked to the limited knowledge of transport phenomena. The most difficult challenge remains the numerical treatment of turbulence. Some research teams are developing simplified modelling of turbulence in 3D calculations.

Rapid evolution

The above simplified model is not adequate without modification in situations when the composition changes are sufficiently rapid. The equation of hydrostatic equilibrium may need to be modified by adding a radial acceleration term if the radius of the star is changing very quickly, for example if the star is radially pulsating. Also, if the nuclear burning is not stable, or the star's core is rapidly collapsing, an entropy term must be added to the energy equation.