Search This Blog

Tuesday, November 28, 2023

Mathematics and art

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Mathematics_and_art
Mathematics in art: Albrecht Dürer's copper plate engraving Melencolia I, 1514. Mathematical references include a compass for geometry, a magic square and a truncated rhombohedron, while measurement is indicated by the scales and hourglass.
Wireframe drawing of a vase as a solid of revolution by Paolo Uccello. 15th century

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.

Mathematics and art have a long historical relationship. Artists have used mathematics since the 4th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions conjectured to have been based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient art and architecture, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De divina proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of the golden ratio in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesburg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim. In Islamic art, symmetries are evident in forms as varied as Persian girih and Moroccan zellige tilework, Mughal jali pierced stone screens, and widespread muqarnas vaulting.

Mathematics has directly influenced art with conceptual tools such as linear perspective, the analysis of symmetry, and mathematical objects such as polyhedra and the Möbius strip. Magnus Wenninger creates colourful stellated polyhedra, originally as models for teaching. Mathematical concepts such as recursion and logical paradox can be seen in paintings by René Magritte and in engravings by M. C. Escher. Computer art often makes use of fractals including the Mandelbrot set, and sometimes explores other mathematical objects such as cellular automata. Controversially, the artist David Hockney has argued that artists from the Renaissance onwards made use of the camera lucida to draw precise representations of scenes; the architect Philip Steadman similarly argued that Vermeer used the camera obscura in his distinctively observed paintings.

Other relationships include the algorithmic analysis of artworks by X-ray fluorescence spectroscopy, the finding that traditional batiks from different regions of Java have distinct fractal dimensions, and stimuli to mathematics research, especially Filippo Brunelleschi's theory of perspective, which eventually led to Girard Desargues's projective geometry. A persistent view, based ultimately on the Pythagorean notion of harmony in music, holds that everything was arranged by Number, that God is the geometer of the world, and that therefore the world's geometry is sacred.

Origins: from ancient Greece to the Renaissance

Further information: Artistic canons of body proportions

Polykleitos's Canon and symmetria

Roman copy in marble of Doryphoros, originally a bronze by Polykleitos
Further information: Polykleitos

Polykleitos the elder (c. 450–420 BC) was a Greek sculptor from the school of Argos, and a contemporary of Phidias. His works and statues consisted mainly of bronze and were of athletes. According to the philosopher and mathematician Xenocrates, Polykleitos is ranked as one of the most important sculptors of classical antiquity for his work on the Doryphorus and the statue of Hera in the Heraion of Argos. While his sculptures may not be as famous as those of Phidias, they are much admired. In his Canon, a treatise he wrote designed to document the "perfect" body proportions of the male nude, Polykleitos gives us a mathematical approach towards sculpturing the human body.

The Canon itself has been lost but it is conjectured that Polykleitos used a sequence of proportions where each length is that of the diagonal of a square drawn on its predecessor, 1:√2 (about 1:1.4142).

The influence of the Canon of Polykleitos is immense in Classical Greek, Roman, and Renaissance sculpture, with many sculptors following Polykleitos's prescription. While none of Polykleitos's original works survive, Roman copies demonstrate his ideal of physical perfection and mathematical precision. Some scholars argue that Pythagorean thought influenced the Canon of Polykleitos. The Canon applies the basic mathematical concepts of Greek geometry, such as the ratio, proportion, and symmetria (Greek for "harmonious proportions") and turns it into a system capable of describing the human form through a series of continuous geometric progressions.

Perspective and proportion

Main article: Perspective (graphical)
Brunelleschi's experiment with linear perspective

In classical times, rather than making distant figures smaller with linear perspective, painters sized objects and figures according to their thematic importance. In the Middle Ages, some artists used reverse perspective for special emphasis. The Muslim mathematician Alhazen (Ibn al-Haytham) described a theory of optics in his Book of Optics in 1021, but never applied it to art. The Renaissance saw a rebirth of Classical Greek and Roman culture and ideas, among them the study of mathematics to understand nature and the arts. Two major motives drove artists in the late Middle Ages and the Renaissance towards mathematics. First, painters needed to figure out how to depict three-dimensional scenes on a two-dimensional canvas. Second, philosophers and artists alike were convinced that mathematics was the true essence of the physical world and that the entire universe, including the arts, could be explained in geometric terms.

The rudiments of perspective arrived with Giotto (1266/7 – 1337), who attempted to draw in perspective using an algebraic method to determine the placement of distant lines. In 1415, the Italian architect Filippo Brunelleschi and his friend Leon Battista Alberti demonstrated the geometrical method of applying perspective in Florence, using similar triangles as formulated by Euclid, to find the apparent height of distant objects. Brunelleschi's own perspective paintings are lost, but Masaccio's painting of the Holy Trinity shows his principles at work.

Paolo Uccello made innovative use of perspective in The Battle of San Romano (c. 1435–1460).

The Italian painter Paolo Uccello (1397–1475) was fascinated by perspective, as shown in his paintings of The Battle of San Romano (c. 1435–1460): broken lances lie conveniently along perspective lines.

The painter Piero della Francesca (c. 1415–1492) exemplified this new shift in Italian Renaissance thinking. He was an expert mathematician and geometer, writing books on solid geometry and perspective, including De prospectiva pingendi (On Perspective for Painting), Trattato d'Abaco (Abacus Treatise), and De quinque corporibus regularibus (On the Five Regular Solids). The historian Vasari in his Lives of the Painters calls Piero the "greatest geometer of his time, or perhaps of any time." Piero's interest in perspective can be seen in his paintings including the Polyptych of Perugia, the San Agostino altarpiece and The Flagellation of Christ. His work on geometry influenced later mathematicians and artists including Luca Pacioli in his De divina proportione and Leonardo da Vinci. Piero studied classical mathematics and the works of Archimedes. He was taught commercial arithmetic in "abacus schools"; his writings are formatted like abacus school textbooks, perhaps including Leonardo Pisano (Fibonacci)'s 1202 Liber Abaci. Linear perspective was just being introduced into the artistic world. Alberti explained in his 1435 De pictura: "light rays travel in straight lines from points in the observed scene to the eye, forming a kind of pyramid with the eye as vertex." A painting constructed with linear perspective is a cross-section of that pyramid.

In De Prospectiva Pingendi, Piero transforms his empirical observations of the way aspects of a figure change with point of view into mathematical proofs. His treatise starts in the vein of Euclid: he defines the point as "the tiniest thing that is possible for the eye to comprehend". He uses deductive logic to lead the reader to the perspective representation of a three-dimensional body.

The artist David Hockney argued in his book Secret Knowledge: Rediscovering the Lost Techniques of the Old Masters that artists started using a camera lucida from the 1420s, resulting in a sudden change in precision and realism, and that this practice was continued by major artists including Ingres, Van Eyck, and Caravaggio. Critics disagree on whether Hockney was correct. Similarly, the architect Philip Steadman argued controversially that Vermeer had used a different device, the camera obscura, to help him create his distinctively observed paintings.

In 1509, Luca Pacioli (c. 1447–1517) published De divina proportione on mathematical and artistic proportion, including in the human face. Leonardo da Vinci (1452–1519) illustrated the text with woodcuts of regular solids while he studied under Pacioli in the 1490s. Leonardo's drawings are probably the first illustrations of skeletonic solids. These, such as the rhombicuboctahedron, were among the first to be drawn to demonstrate perspective by being overlaid on top of each other. The work discusses perspective in the works of Piero della Francesca, Melozzo da Forlì, and Marco Palmezzano. Leonardo studied Pacioli's Summa, from which he copied tables of proportions. In Mona Lisa and The Last Supper, Leonardo's work incorporated linear perspective with a vanishing point to provide apparent depth. The Last Supper is constructed in a tight ratio of 12:6:4:3, as is Raphael's The School of Athens, which includes Pythagoras with a tablet of ideal ratios, sacred to the Pythagoreans. In Vitruvian Man, Leonardo expressed the ideas of the Roman architect Vitruvius, innovatively showing the male figure twice, and centring him in both a circle and a square.

As early as the 15th century, curvilinear perspective found its way into paintings by artists interested in image distortions. Jan van Eyck's 1434 Arnolfini Portrait contains a convex mirror with reflections of the people in the scene, while Parmigianino's Self-portrait in a Convex Mirror, c. 1523–1524, shows the artist's largely undistorted face at the centre, with a strongly curved background and artist's hand around the edge.

Three-dimensional space can be represented convincingly in art, as in technical drawing, by means other than perspective. Oblique projections, including cavalier perspective (used by French military artists to depict fortifications in the 18th century), were used continuously and ubiquitously by Chinese artists from the first or second centuries until the 18th century. The Chinese acquired the technique from India, which acquired it from Ancient Rome. Oblique projection is seen in Japanese art, such as in the Ukiyo-e paintings of Torii Kiyonaga (1752–1815).

Golden ratio

Further information: List of works designed with the golden ratio

The golden ratio (roughly equal to 1.618) was known to Euclid. The golden ratio has persistently been claimed in modern times to have been used in art and architecture by the ancients in Egypt, Greece and elsewhere, without reliable evidence. The claim may derive from confusion with "golden mean", which to the Ancient Greeks meant "avoidance of excess in either direction", not a ratio. Pyramidologists since the 19th century have argued on dubious mathematical grounds for the golden ratio in pyramid design. The Parthenon, a 5th-century BC temple in Athens, has been claimed to use the golden ratio in its façade and floor plan, but these claims too are disproved by measurement. The Great Mosque of Kairouan in Tunisia has similarly been claimed to use the golden ratio in its design, but the ratio does not appear in the original parts of the mosque. The historian of architecture Frederik Macody Lund argued in 1919 that the Cathedral of Chartres (12th century), Notre-Dame of Laon (1157–1205) and Notre Dame de Paris (1160) are designed according to the golden ratio, drawing regulator lines to make his case. Other scholars argue that until Pacioli's work in 1509, the golden ratio was unknown to artists and architects. For example, the height and width of the front of Notre-Dame of Laon have the ratio 8/5 or 1.6, not 1.618. Such Fibonacci ratios quickly become hard to distinguish from the golden ratio. After Pacioli, the golden ratio is more definitely discernible in artworks including Leonardo's Mona Lisa.

Another ratio, the only other morphic number, was named the plastic number in 1928 by the Dutch architect Hans van der Laan (originally named le nombre radiant in French). Its value is the solution of the cubic equation

,

an irrational number which is approximately 1.325. According to the architect Richard Padovan, this has characteristic ratios 3/4 and 1/7, which govern the limits of human perception in relating one physical size to another. Van der Laan used these ratios when designing the 1967 St. Benedictusberg Abbey church in the Netherlands.

Planar symmetries

Further information: Planar symmetry, Wallpaper group, Islamic geometric patterns, and Kilim
Powerful presence: carpet with double medallion. Central Anatolia (Konya – Karapınar), turn of the 16th/17th centuries. Alâeddin Mosque

Planar symmetries have for millennia been exploited in artworks such as carpets, lattices, textiles and tilings.

Many traditional rugs, whether pile carpets or flatweave kilims, are divided into a central field and a framing border; both can have symmetries, though in handwoven carpets these are often slightly broken by small details, variations of pattern and shifts in colour introduced by the weaver. In kilims from Anatolia, the motifs used are themselves usually symmetrical. The general layout, too, is usually present, with arrangements such as stripes, stripes alternating with rows of motifs, and packed arrays of roughly hexagonal motifs. The field is commonly laid out as a wallpaper with a wallpaper group such as pmm, while the border may be laid out as a frieze of frieze group pm11, pmm2 or pma2. Turkish and Central Asian kilims often have three or more borders in different frieze groups. Weavers certainly had the intention of symmetry, without explicit knowledge of its mathematics. The mathematician and architectural theorist Nikos Salingaros suggests that the "powerful presence" (aesthetic effect) of a "great carpet" such as the best Konya two-medallion carpets of the 17th century is created by mathematical techniques related to the theories of the architect Christopher Alexander. These techniques include making opposites couple; opposing colour values; differentiating areas geometrically, whether by using complementary shapes or balancing the directionality of sharp angles; providing small-scale complexity (from the knot level upwards) and both small- and large-scale symmetry; repeating elements at a hierarchy of different scales (with a ratio of about 2.7 from each level to the next). Salingaros argues that "all successful carpets satisfy at least nine of the above ten rules", and suggests that it might be possible to create a metric from these rules.

Elaborate lattices are found in Indian Jali work, carved in marble to adorn tombs and palaces. Chinese lattices, always with some symmetry, exist in 14 of the 17 wallpaper groups; they often have mirror, double mirror, or rotational symmetry. Some have a central medallion, and some have a border in a frieze group. Many Chinese lattices have been analysed mathematically by Daniel S. Dye; he identifies Sichuan as the centre of the craft.

Girih tiles

Symmetries are prominent in textile arts including quilting, knitting, cross-stitch, crochet, embroidery and weaving, where they may be purely decorative or may be marks of status. Rotational symmetry is found in circular structures such as domes; these are sometimes elaborately decorated with symmetric patterns inside and out, as at the 1619 Sheikh Lotfollah Mosque in Isfahan. Items of embroidery and lace work such as tablecloths and table mats, made using bobbins or by tatting, can have a wide variety of reflectional and rotational symmetries which are being explored mathematically.

Islamic art exploits symmetries in many of its artforms, notably in girih tilings. These are formed using a set of five tile shapes, namely a regular decagon, an elongated hexagon, a bow tie, a rhombus, and a regular pentagon. All the sides of these tiles have the same length; and all their angles are multiples of 36° (π/5 radians), offering fivefold and tenfold symmetries. The tiles are decorated with strapwork lines (girih), generally more visible than the tile boundaries. In 2007, the physicists Peter Lu and Paul Steinhardt argued that girih resembled quasicrystalline Penrose tilings. Elaborate geometric zellige tilework is a distinctive element in Moroccan architecture. Muqarnas vaults are three-dimensional but were designed in two dimensions with drawings of geometrical cells.

Polyhedra

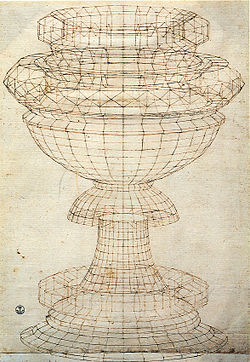
The Platonic solids and other polyhedra are a recurring theme in Western art. They are found, for instance, in a marble mosaic featuring the small stellated dodecahedron, attributed to Paolo Uccello, in the floor of the San Marco Basilica in Venice; in Leonardo da Vinci's diagrams of regular polyhedra drawn as illustrations for Luca Pacioli's 1509 book The Divine Proportion; as a glass rhombicuboctahedron in Jacopo de Barbari's portrait of Pacioli, painted in 1495; in the truncated polyhedron (and various other mathematical objects) in Albrecht Dürer's engraving Melencolia I; and in Salvador Dalí's painting The Last Supper in which Christ and his disciples are pictured inside a giant dodecahedron.

Albrecht Dürer (1471–1528) was a German Renaissance printmaker who made important contributions to polyhedral literature in his 1525 book, Underweysung der Messung (Education on Measurement), meant to teach the subjects of linear perspective, geometry in architecture, Platonic solids, and regular polygons. Dürer was likely influenced by the works of Luca Pacioli and Piero della Francesca during his trips to Italy. While the examples of perspective in Underweysung der Messung are underdeveloped and contain inaccuracies, there is a detailed discussion of polyhedra. Dürer is also the first to introduce in text the idea of polyhedral nets, polyhedra unfolded to lie flat for printing. Dürer published another influential book on human proportions called Vier Bücher von Menschlicher Proportion (Four Books on Human Proportion) in 1528.

Dürer's well-known engraving Melencolia I depicts a frustrated thinker sitting by a truncated triangular trapezohedron and a magic square. These two objects, and the engraving as a whole, have been the subject of more modern interpretation than the contents of almost any other print, including a two-volume book by Peter-Klaus Schuster, and an influential discussion in Erwin Panofsky's monograph of Dürer.

Salvador Dalí's 1954 painting Corpus Hypercubus uniquely depicts the cross of Christ as an unfolded three-dimensional net for a hypercube, also known as a tesseract: the unfolding of a tesseract into these eight cubes is analogous to unfolding the sides of a cube into a cross shape of six squares, here representing the divine perspective with a four-dimensional regular polyhedron. The painting shows the figure of Christ in front of the tessaract; he would normally be shown fixed with nails to the cross, but there are no nails in the painting. Instead, there are four small cubes in front of his body, at the corners of the frontmost of the eight tessaract cubes. The mathematician Thomas Banchoff states that Dalí was trying to go beyond the three-dimensional world, while the poet and art critic Kelly Grovier says that "The painting seems to have cracked the link between the spirituality of Christ's salvation and the materiality of geometric and physical forces. It appears to bridge the divide that many feel separates science from religion."

Fractal dimensions

Batiks from Surakarta, Java, like this parang klithik sword pattern, have a fractal dimension between 1.2 and 1.5.

Traditional Indonesian wax-resist batik designs on cloth combine representational motifs (such as floral and vegetal elements) with abstract and somewhat chaotic elements, including imprecision in applying the wax resist, and random variation introduced by cracking of the wax. Batik designs have a fractal dimension between 1 and 2, varying in different regional styles. For example, the batik of Cirebon has a fractal dimension of 1.1; the batiks of Yogyakarta and Surakarta (Solo) in Central Java have a fractal dimension of 1.2 to 1.5; and the batiks of Lasem on the north coast of Java and of Tasikmalaya in West Java have a fractal dimension between 1.5 and 1.7.

The drip painting works of the modern artist Jackson Pollock are similarly distinctive in their fractal dimension. His 1948 Number 14 has a coastline-like dimension of 1.45, while his later paintings had successively higher fractal dimensions and accordingly more elaborate patterns. One of his last works, Blue Poles, took six months to create, and has the fractal dimension of 1.72.

A complex relationship

The astronomer Galileo Galilei in his Il Saggiatore wrote that "[The universe] is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures." Artists who strive and seek to study nature must first, in Galileo's view, fully understand mathematics. Mathematicians, conversely, have sought to interpret and analyse art through the lens of geometry and rationality. The mathematician Felipe Cucker suggests that mathematics, and especially geometry, is a source of rules for "rule-driven artistic creation", though not the only one. Some of the many strands of the resulting complex relationship are described below.

The mathematician G. H. Hardy defined a set of criteria for mathematical beauty.

Mathematics as an art

Main article: Mathematical beauty

The mathematician Jerry P. King describes mathematics as an art, stating that "the keys to mathematics are beauty and elegance and not dullness and technicality", and that beauty is the motivating force for mathematical research. King cites the mathematician G. H. Hardy's 1940 essay A Mathematician's Apology. In it, Hardy discusses why he finds two theorems of classical times as first rate, namely Euclid's proof there are infinitely many prime numbers, and the proof that the square root of 2 is irrational. King evaluates this last against Hardy's criteria for mathematical elegance: "seriousness, depth, generality, unexpectedness, inevitability, and economy" (King's italics), and describes the proof as "aesthetically pleasing". The Hungarian mathematician Paul Erdős agreed that mathematics possessed beauty but considered the reasons beyond explanation: "Why are numbers beautiful? It's like asking why is Beethoven's Ninth Symphony beautiful. If you don't see why, someone can't tell you. I know numbers are beautiful."

Mathematical tools for art

Further information: List of mathematical artists, fractal art, and computer art

Mathematics can be discerned in many of the arts, such as music, dance, painting, architecture, and sculpture. Each of these is richly associated with mathematics. Among the connections to the visual arts, mathematics can provide tools for artists, such as the rules of linear perspective as described by Brook Taylor and Johann Lambert, or the methods of descriptive geometry, now applied in software modelling of solids, dating back to Albrecht Dürer and Gaspard Monge. Artists from Luca Pacioli in the Middle Ages and Leonardo da Vinci and Albrecht Dürer in the Renaissance have made use of and developed mathematical ideas in the pursuit of their artistic work. The use of perspective began, despite some embryonic usages in the architecture of Ancient Greece, with Italian painters such as Giotto in the 13th century; rules such as the vanishing point were first formulated by Brunelleschi in about 1413, his theory influencing Leonardo and Dürer. Isaac Newton's work on the optical spectrum influenced Goethe's Theory of Colours and in turn artists such as Philipp Otto Runge, J. M. W. Turner, the Pre-Raphaelites and Wassily Kandinsky. Artists may also choose to analyse the symmetry of a scene. Tools may be applied by mathematicians who are exploring art, or artists inspired by mathematics, such as M. C. Escher (inspired by H. S. M. Coxeter) and the architect Frank Gehry, who more tenuously argued that computer aided design enabled him to express himself in a wholly new way.

Octopod by Mikael Hvidtfeldt Christensen. Algorithmic art produced with the software Structure Synth

The artist Richard Wright argues that mathematical objects that can be constructed can be seen either "as processes to simulate phenomena" or as works of "computer art". He considers the nature of mathematical thought, observing that fractals were known to mathematicians for a century before they were recognised as such. Wright concludes by stating that it is appropriate to subject mathematical objects to any methods used to "come to terms with cultural artifacts like art, the tension between objectivity and subjectivity, their metaphorical meanings and the character of representational systems." He gives as instances an image from the Mandelbrot set, an image generated by a cellular automaton algorithm, and a computer-rendered image, and discusses, with reference to the Turing test, whether algorithmic products can be art. Sasho Kalajdzievski's Math and Art: An Introduction to Visual Mathematics takes a similar approach, looking at suitably visual mathematics topics such as tilings, fractals and hyperbolic geometry.

Some of the first works of computer art were created by Desmond Paul Henry's "Drawing Machine 1", an analogue machine based on a bombsight computer and exhibited in 1962. The machine was capable of creating complex, abstract, asymmetrical, curvilinear, but repetitive line drawings. More recently, Hamid Naderi Yeganeh has created shapes suggestive of real world objects such as fish and birds, using formulae that are successively varied to draw families of curves or angled lines. Artists such as Mikael Hvidtfeldt Christensen create works of generative or algorithmic art by writing scripts for a software system such as Structure Synth: the artist effectively directs the system to apply a desired combination of mathematical operations to a chosen set of data.

From mathematics to art

Proto-Cubism: Pablo Picasso's 1907 painting Les Demoiselles d'Avignon uses a fourth dimension projection to show a figure both full face and in profile.
Further information: Proto-Cubism, tessellation, M. C. Escher, Mathematics of paper folding, and Mathematics and fiber arts

The mathematician and theoretical physicist Henri Poincaré's Science and Hypothesis was widely read by the Cubists, including Pablo Picasso and Jean Metzinger. Being thoroughly familiar with Bernhard Riemann's work on non-Euclidean geometry, Poincaré was more than aware that Euclidean geometry is just one of many possible geometric configurations, rather than as an absolute objective truth. The possible existence of a fourth dimension inspired artists to question classical Renaissance perspective: non-Euclidean geometry became a valid alternative. The concept that painting could be expressed mathematically, in colour and form, contributed to Cubism, the art movement that led to abstract art. Metzinger, in 1910, wrote that: "[Picasso] lays out a free, mobile perspective, from which that ingenious mathematician Maurice Princet has deduced a whole geometry". Later, Metzinger wrote in his memoirs:

Maurice Princet joined us often ... it was as an artist that he conceptualized mathematics, as an aesthetician that he invoked n-dimensional continuums. He loved to get the artists interested in the new views on space that had been opened up by Schlegel and some others. He succeeded at that.

The impulse to make teaching or research models of mathematical forms naturally creates objects that have symmetries and surprising or pleasing shapes. Some of these have inspired artists such as the Dadaists Man Ray, Marcel Duchamp and Max Ernst, and following Man Ray, Hiroshi Sugimoto.

Enneper surfaces as Dadaism: Man Ray's 1934 Objet mathematique

Man Ray photographed some of the mathematical models in the Institut Henri Poincaré in Paris, including Objet mathematique (Mathematical object). He noted that this represented Enneper surfaces with constant negative curvature, derived from the pseudo-sphere. This mathematical foundation was important to him, as it allowed him to deny that the object was "abstract", instead claiming that it was as real as the urinal that Duchamp made into a work of art. Man Ray admitted that the object's [Enneper surface] formula "meant nothing to me, but the forms themselves were as varied and authentic as any in nature." He used his photographs of the mathematical models as figures in his series he did on Shakespeare's plays, such as his 1934 painting Antony and Cleopatra. The art reporter Jonathan Keats, writing in ForbesLife, argues that Man Ray photographed "the elliptic paraboloids and conic points in the same sensual light as his pictures of Kiki de Montparnasse", and "ingeniously repurposes the cool calculations of mathematics to reveal the topology of desire". Twentieth century sculptors such as Henry Moore, Barbara Hepworth and Naum Gabo took inspiration from mathematical models. Moore wrote of his 1938 Stringed Mother and Child: "Undoubtedly the source of my stringed figures was the Science Museum ... I was fascinated by the mathematical models I saw there ... It wasn't the scientific study of these models but the ability to look through the strings as with a bird cage and to see one form within another which excited me."

Theo van Doesburg's Six Moments in the Development of Plane to Space, 1926 or 1929

The artists Theo van Doesburg and Piet Mondrian founded the De Stijl movement, which they wanted to "establish a visual vocabulary comprised of elementary geometrical forms comprehensible by all and adaptable to any discipline". Many of their artworks visibly consist of ruled squares and triangles, sometimes also with circles. De Stijl artists worked in painting, furniture, interior design and architecture. After the breakup of De Stijl, Van Doesburg founded the Avant-garde Art Concret movement, describing his 1929–1930 Arithmetic Composition, a series of four black squares on the diagonal of a squared background, as "a structure that can be controlled, a definite surface without chance elements or individual caprice", yet "not lacking in spirit, not lacking the universal and not ... empty as there is everything which fits the internal rhythm". The art critic Gladys Fabre observes that two progressions are at work in the painting, namely the growing black squares and the alternating backgrounds.

The mathematics of tessellation, polyhedra, shaping of space, and self-reference provided the graphic artist M. C. Escher (1898—1972) with a lifetime's worth of materials for his woodcuts. In the Alhambra Sketch, Escher showed that art can be created with polygons or regular shapes such as triangles, squares, and hexagons. Escher used irregular polygons when tiling the plane and often used reflections, glide reflections, and translations to obtain further patterns. Many of his works contain impossible constructions, made using geometrical objects which set up a contradiction between perspective projection and three dimensions, but are pleasant to the human sight. Escher's Ascending and Descending is based on the "impossible staircase" created by the medical scientist Lionel Penrose and his son the mathematician Roger Penrose.

Some of Escher's many tessellation drawings were inspired by conversations with the mathematician H. S. M. Coxeter on hyperbolic geometry. Escher was especially interested in five specific polyhedra, which appear many times in his work. The Platonic solids—tetrahedrons, cubes, octahedrons, dodecahedrons, and icosahedrons—are especially prominent in Order and Chaos and Four Regular Solids. These stellated figures often reside within another figure which further distorts the viewing angle and conformation of the polyhedrons and provides a multifaceted perspective artwork.

The visual intricacy of mathematical structures such as tessellations and polyhedra have inspired a variety of mathematical artworks. Stewart Coffin makes polyhedral puzzles in rare and beautiful woods; George W. Hart works on the theory of polyhedra and sculpts objects inspired by them; Magnus Wenninger makes "especially beautiful" models of complex stellated polyhedra.

The distorted perspectives of anamorphosis have been explored in art since the sixteenth century, when Hans Holbein the Younger incorporated a severely distorted skull in his 1533 painting The Ambassadors. Many artists since then, including Escher, have make use of anamorphic tricks.

The mathematics of topology has inspired several artists in modern times. The sculptor John Robinson (1935–2007) created works such as Gordian Knot and Bands of Friendship, displaying knot theory in polished bronze. Other works by Robinson explore the topology of toruses. Genesis is based on Borromean rings – a set of three circles, no two of which link but in which the whole structure cannot be taken apart without breaking. The sculptor Helaman Ferguson creates complex surfaces and other topological objects. His works are visual representations of mathematical objects; The Eightfold Way is based on the projective special linear group PSL(2,7), a finite group of 168 elements. The sculptor Bathsheba Grossman similarly bases her work on mathematical structures. The artist Nelson Saiers incorporates mathematical concepts and theorems in his art from toposes and schemes to the four color theorem and the irrationality of π.

A liberal arts inquiry project examines connections between mathematics and art through the Möbius strip, flexagons, origami and panorama photography.

Mathematical objects including the Lorenz manifold and the hyperbolic plane have been crafted using fiber arts including crochet. The American weaver Ada Dietz wrote a 1949 monograph Algebraic Expressions in Handwoven Textiles, defining weaving patterns based on the expansion of multivariate polynomials. The mathematician Daina Taimiņa demonstrated features of the hyperbolic plane by crocheting in 2001. This led Margaret and Christine Wertheim to crochet a coral reef, consisting of many marine animals such as nudibranchs whose shapes are based on hyperbolic planes. The mathematician J. C. P. Miller used the Rule 90 cellular automaton to design tapestries depicting both trees and abstract patterns of triangles. The "mathekniticians" Pat Ashforth and Steve Plummer use knitted versions of mathematical objects such as hexaflexagons in their teaching, though their Menger sponge proved too troublesome to knit and was made of plastic canvas instead. Their "mathghans" (Afghans for Schools) project introduced knitting into the British mathematics and technology curriculum.

Semiotic joke: René Magritte's La condition humaine 1933

Illustrating mathematics

Front face of Giotto's Stefaneschi Triptych, 1320 illustrates recursion.
Detail of Cardinal Stefaneschi holding the triptych

Modelling is far from the only possible way to illustrate mathematical concepts. Giotto's Stefaneschi Triptych, 1320, illustrates recursion in the form of mise en abyme; the central panel of the triptych contains, lower left, the kneeling figure of Cardinal Stefaneschi, holding up the triptych as an offering. Giorgio de Chirico's metaphysical paintings such as his 1917 Great Metaphysical Interior explore the question of levels of representation in art by depicting paintings within his paintings.

Art can exemplify logical paradoxes, as in some paintings by the surrealist René Magritte, which can be read as semiotic jokes about confusion between levels. In La condition humaine (1933), Magritte depicts an easel (on the real canvas), seamlessly supporting a view through a window which is framed by "real" curtains in the painting. Similarly, Escher's Print Gallery (1956) is a print which depicts a distorted city which contains a gallery which recursively contains the picture, and so ad infinitum. Magritte made use of spheres and cuboids to distort reality in a different way, painting them alongside an assortment of houses in his 1931 Mental Arithmetic as if they were children's building blocks, but house-sized. The Guardian observed that the "eerie toytown image" prophesied Modernism's usurpation of "cosy traditional forms", but also plays with the human tendency to seek patterns in nature.

Diagram of the apparent paradox embodied in M. C. Escher's 1956 lithograph Print Gallery, as discussed by Douglas Hofstadter in his 1980 book Gödel, Escher, Bach

Salvador Dalí's last painting, The Swallow's Tail (1983), was part of a series inspired by René Thom's catastrophe theory. The Spanish painter and sculptor Pablo Palazuelo (1916–2007) focused on the investigation of form. He developed a style that he described as the geometry of life and the geometry of all nature. Consisting of simple geometric shapes with detailed patterning and coloring, in works such as Angular I and Automnes, Palazuelo expressed himself in geometric transformations.

The artist Adrian Gray practises stone balancing, exploiting friction and the centre of gravity to create striking and seemingly impossible compositions.

Lithograph Print Gallery by M. C. Escher, 1956

Artists, however, do not necessarily take geometry literally. As Douglas Hofstadter writes in his 1980 reflection on human thought, Gödel, Escher, Bach, by way of (among other things) the mathematics of art: "The difference between an Escher drawing and non-Euclidean geometry is that in the latter, comprehensible interpretations can be found for the undefined terms, resulting in a comprehensible total system, whereas for the former, the end result is not reconcilable with one's conception of the world, no matter how long one stares at the pictures." Hofstadter discusses the seemingly paradoxical lithograph Print Gallery by M. C. Escher; it depicts a seaside town containing an art gallery which seems to contain a painting of the seaside town, there being a "strange loop, or tangled hierarchy" to the levels of reality in the image. The artist himself, Hofstadter observes, is not seen; his reality and his relation to the lithograph are not paradoxical. The image's central void has also attracted the interest of mathematicians Bart de Smit and Hendrik Lenstra, who propose that it could contain a Droste effect copy of itself, rotated and shrunk; this would be a further illustration of recursion beyond that noted by Hofstadter.

Analysis of art history

Algorithmic analysis of images of artworks, for example using X-ray fluorescence spectroscopy, can reveal information about art. Such techniques can uncover images in layers of paint later covered over by an artist; help art historians to visualize an artwork before it cracked or faded; help to tell a copy from an original, or distinguish the brushstroke style of a master from those of his apprentices.

Max Ernst making Lissajous figures, New York, 1942

Jackson Pollock's drip painting style has a definite fractal dimension; among the artists who may have influenced Pollock's controlled chaos, Max Ernst painted Lissajous figures directly by swinging a punctured bucket of paint over a canvas.

The computer scientist Neil Dodgson investigated whether Bridget Riley's stripe paintings could be characterised mathematically, concluding that while separation distance could "provide some characterisation" and global entropy worked on some paintings, autocorrelation failed as Riley's patterns were irregular. Local entropy worked best, and correlated well with the description given by the art critic Robert Kudielka.

The American mathematician George Birkhoff's 1933 Aesthetic Measure proposes a quantitative metric of the aesthetic quality of an artwork. It does not attempt to measure the connotations of a work, such as what a painting might mean, but is limited to the "elements of order" of a polygonal figure. Birkhoff first combines (as a sum) five such elements: whether there is a vertical axis of symmetry; whether there is optical equilibrium; how many rotational symmetries it has; how wallpaper-like the figure is; and whether there are unsatisfactory features such as having two vertices too close together. This metric, O, takes a value between −3 and 7. The second metric, C, counts elements of the figure, which for a polygon is the number of different straight lines containing at least one of its sides. Birkhoff then defines his aesthetic measure of an object's beauty as O/C. This can be interpreted as a balance between the pleasure looking at the object gives, and the amount of effort needed to take it in. Birkhoff's proposal has been criticized in various ways, not least for trying to put beauty in a formula, but he never claimed to have done that.

Stimuli to mathematical research

Further information: Projective geometry and Mathematics of paper folding

Art has sometimes stimulated the development of mathematics, as when Brunelleschi's theory of perspective in architecture and painting started a cycle of research that led to the work of Brook Taylor and Johann Heinrich Lambert on the mathematical foundations of perspective drawing, and ultimately to the mathematics of projective geometry of Girard Desargues and Jean-Victor Poncelet.

The Japanese paper-folding art of origami has been reworked mathematically by Tomoko Fusé using modules, congruent pieces of paper such as squares, and making them into polyhedra or tilings. Paper-folding was used in 1893 by T. Sundara Rao in his Geometric Exercises in Paper Folding to demonstrate geometrical proofs. The mathematics of paper folding has been explored in Maekawa's theorem, Kawasaki's theorem, and the Huzita–Hatori axioms.

Illusion to Op art

Further information: Op art
The Fraser spiral illusion, named for Sir James Fraser who discovered it in 1908.

Optical illusions such as the Fraser spiral strikingly demonstrate limitations in human visual perception, creating what the art historian Ernst Gombrich called a "baffling trick." The black and white ropes that appear to form spirals are in fact concentric circles. The mid-twentieth century Op art or optical art style of painting and graphics exploited such effects to create the impression of movement and flashing or vibrating patterns seen in the work of artists such as Bridget Riley, Spyros Horemis, and Victor Vasarely.

Sacred geometry

Further information: Sacred geometry and Mathematics and music

A strand of art from Ancient Greece onwards sees God as the geometer of the world, and the world's geometry therefore as sacred. The belief that God created the universe according to a geometric plan has ancient origins. Plutarch attributed the belief to Plato, writing that "Plato said God geometrizes continually" (Convivialium disputationum, liber 8,2). This image has influenced Western thought ever since. The Platonic concept derived in its turn from a Pythagorean notion of harmony in music, where the notes were spaced in perfect proportions, corresponding to the lengths of the lyre's strings; indeed, the Pythagoreans held that everything was arranged by Number. In the same way, in Platonic thought, the regular or Platonic solids dictate the proportions found in nature, and in art. An illumination in the 13th-century Codex Vindobonensis shows God drawing out the universe with a pair of compasses, which may refer to a verse in the Old Testament: "When he established the heavens I was there: when he set a compass upon the face of the deep" (Proverbs 8:27), . In 1596, the mathematical astronomer Johannes Kepler modelled the universe as a set of nested Platonic solids, determining the relative sizes of the orbits of the planets. William Blake's Ancient of Days (depicting Urizen, Blake's embodiment of reason and law) and his painting of the physicist Isaac Newton, naked, hunched and drawing with a compass, use the symbolism of compasses to critique conventional reason and materialism as narrow-minded. Salvador Dalí's 1954 Crucifixion (Corpus Hypercubus) depicts the cross as a hypercube, representing the divine perspective with four dimensions rather than the usual three. In Dalí's The Sacrament of the Last Supper (1955) Christ and his disciples are pictured inside a giant dodecahedron.

at

Bytecode

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Bytecode
 
Bytecode (also called portable code or p-code) is a form of instruction set designed for efficient execution by a software interpreter. Unlike human-readable source code, bytecodes are compact numeric codes, constants, and references (normally numeric addresses) that encode the result of compiler parsing and performing semantic analysis of things like type, scope, and nesting depths of program objects.

The name bytecode stems from instruction sets that have one-byte opcodes followed by optional parameters. Intermediate representations such as bytecode may be output by programming language implementations to ease interpretation, or it may be used to reduce hardware and operating system dependence by allowing the same code to run cross-platform, on different devices. Bytecode may often be either directly executed on a virtual machine (a p-code machine, i.e., interpreter), or it may be further compiled into machine code for better performance.

Since bytecode instructions are processed by software, they may be arbitrarily complex, but are nonetheless often akin to traditional hardware instructions: virtual stack machines are the most common, but virtual register machines have been built also. Different parts may often be stored in separate files, similar to object modules, but dynamically loaded during execution.

Execution

A bytecode program may be executed by parsing and directly executing the instructions, one at a time. This kind of bytecode interpreter is very portable. Some systems, called dynamic translators, or just-in-time (JIT) compilers, translate bytecode into machine code as necessary at runtime. This makes the virtual machine hardware-specific but does not lose the portability of the bytecode. For example, Java and Smalltalk code is typically stored in bytecode format, which is typically then JIT compiled to translate the bytecode to machine code before execution. This introduces a delay before a program is run, when the bytecode is compiled to native machine code, but improves execution speed considerably compared to interpreting source code directly, normally by around an order of magnitude (10x).

Because of its performance advantage, today many language implementations execute a program in two phases, first compiling the source code into bytecode, and then passing the bytecode to the virtual machine. There are bytecode based virtual machines of this sort for Java, Raku, Python, PHP,[a] Tcl, mawk and Forth (however, Forth is seldom compiled via bytecodes in this way, and its virtual machine is more generic instead). The implementation of Perl and Ruby 1.8 instead work by walking an abstract syntax tree representation derived from the source code.

More recently, the authors of V8 and Dart have challenged the notion that intermediate bytecode is needed for fast and efficient VM implementation. Both of these language implementations currently do direct JIT compiling from source code to machine code with no bytecode intermediary.

Examples

(disassemble '(lambda (x) (print x)))
; disassembly for (LAMBDA (X))
; 2436F6DF:       850500000F22     TEST EAX, [#x220F0000]     ; no-arg-parsing entry point
;       E5:       8BD6             MOV EDX, ESI
;       E7:       8B05A8F63624     MOV EAX, [#x2436F6A8]      ; #<FDEFINITION object for PRINT>
;       ED:       B904000000       MOV ECX, 4
;       F2:       FF7504           PUSH DWORD PTR [EBP+4]
;       F5:       FF6005           JMP DWORD PTR [EAX+5]
;       F8:       CC0A             BREAK 10                   ; error trap
;       FA:       02               BYTE #X02
;       FB:       18               BYTE #X18                  ; INVALID-ARG-COUNT-ERROR
;       FC:       4F               BYTE #X4F                  ; ECX
Compiled code can be analysed and investigated using a built-in tool for debugging the low-level bytecode. The tool can be initialized from the shell, for example:
>>> import dis # "dis" - Disassembler of Python byte code into mnemonics.
>>> dis.dis('print("Hello, World!")')
  1           0 LOAD_NAME                0 (print)
              2 LOAD_CONST               0 ('Hello, World!')
              4 CALL_FUNCTION            1
              6 RETURN_VALUE
at

Monday, November 27, 2023

Programmable logic controller

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Programmable_logic_controller

PLCs for a monitoring system in the pharmaceutical industry

A programmable logic controller (PLC) or programmable controller is an industrial computer that has been ruggedized and adapted for the control of manufacturing processes, such as assembly lines, machines, robotic devices, or any activity that requires high reliability, ease of programming, and process fault diagnosis.

PLCs can range from small modular devices with tens of inputs and outputs (I/O), in a housing integral with the processor, to large rack-mounted modular devices with thousands of I/O, and which are often networked to other PLC and SCADA systems. They can be designed for many arrangements of digital and analog I/O, extended temperature ranges, immunity to electrical noise, and resistance to vibration and impact.

PLCs were first developed in the automobile manufacturing industry to provide flexible, rugged and easily programmable controllers to replace hard-wired relay logic systems. Dick Morley who invented the first PLC, the Modicon 084, for General Motors in 1968, is considered the father of PLC.

A PLC is an example of a hard real-time system since output results must be produced in response to input conditions within a limited time, otherwise unintended operation may result. Programs to control machine operation are typically stored in battery-backed-up or non-volatile memory.

Invention and early development

PLC originated in the late 1960s in the automotive industry in the US and were designed to replace relay logic systems. Before, control logic for manufacturing was mainly composed of relays, cam timers, drum sequencers, and dedicated closed-loop controllers.

The hard-wired nature made it difficult for design engineers to alter the automation process. Changes would require rewiring and careful updating of the documentation. If even one wire were out of place, or one relay failed, the whole system would become faulty. Often technicians would spend hours troubleshooting by examining the schematics and comparing them to existing wiring. When general-purpose computers became available, they were soon applied to control logic in industrial processes. These early computers were unreliable and required specialist programmers and strict control of working conditions, such as temperature, cleanliness, and power quality.

The PLC provided several advantages over earlier automation systems. It tolerated the industrial environment better than computers and was more reliable, compact and required less maintenance than relay systems. It was easily extensible with additional I/O modules, while relay systems required complicated hardware changes in case of reconfiguration. This allowed for easier iteration over manufacturing process design. With a simple programming language focused on logic and switching operations, it was more user-friendly than computers using general-purpose programming languages. It also permitted its operation to be monitored. Early PLCs were programmed in ladder logic, which strongly resembled a schematic diagram of relay logic.

Modicon

In 1968, GM Hydramatic (the automatic transmission division of General Motors) issued a request for proposals for an electronic replacement for hard-wired relay systems based on a white paper written by engineer Edward R. Clark. The winning proposal came from Bedford Associates from Bedford, Massachusetts. The result was the first PLC—built in 1969–designated the 084, because it was Bedford Associates' eighty-fourth project.

Bedford Associates started a company dedicated to developing, manufacturing, selling, and servicing this new product, which they named Modicon (standing for modular digital controller). One of the people who worked on that project was Dick Morley, who is considered to be the "father" of the PLC. The Modicon brand was sold in 1977 to Gould Electronics and later to Schneider Electric, the current owner. About this same time, Modicon created Modbus, a data communications protocol used with its PLCs. Modbus has since become a standard open protocol commonly used to connect many industrial electrical devices.

One of the first 084 models built is now on display at Schneider Electric's facility in North Andover, Massachusetts. It was presented to Modicon by GM, when the unit was retired after nearly twenty years of uninterrupted service. Modicon used the 84 moniker at the end of its product range until the 984 made its appearance.

Allen-Bradley

In a parallel development Odo Josef Struger is sometimes known as the "father of the programmable logic controller" as well. He was involved in the invention of the Allen‑Bradley programmable logic controller and is credited with inventing the PLC initialism. Allen-Bradley (now a brand owned by Rockwell Automation) became a major PLC manufacturer in the United States during his tenure. Struger played a leadership role in developing IEC 61131-3 PLC programming language standards.

Early methods of programming

Many early PLCs were not capable of graphical representation of the logic, and so it was instead represented as a series of logic expressions in some kind of Boolean format, similar to Boolean algebra. As programming terminals evolved, it became more common for ladder logic to be used, because it was a familiar format used for electro-mechanical control panels. Newer formats, such as state logic and Function Block (which is similar to the way logic is depicted when using digital integrated logic circuits) exist, but they are still not as popular as ladder logic. A primary reason for this is that PLCs solve the logic in a predictable and repeating sequence, and ladder logic allows the person writing the logic to see any issues with the timing of the logic sequence more easily than would be possible in other formats.

Up to the mid-1990s, PLCs were programmed using proprietary programming panels or special-purpose programming terminals, which often had dedicated function keys representing the various logical elements of PLC programs. Some proprietary programming terminals displayed the elements of PLC programs as graphic symbols, but plain ASCII character representations of contacts, coils, and wires were common. Programs were stored on cassette tape cartridges. Facilities for printing and documentation were minimal due to a lack of memory capacity. The oldest PLCs used non-volatile magnetic core memory.

Architecture

A PLC is an industrial microprocessor-based controller with programmable memory used to store program instructions and various functions. It consists of:

  • A processor unit (CPU) which interprets inputs, executes the control program stored in memory and sends output signals,
  • A power supply unit which converts AC voltage to DC,
  • A memory unit storing data from inputs and program to be executed by the processor,
  • An input and output interface, where the controller receives and sends data from/to external devices,
  • A communications interface to receive and transmit data on communication networks from/to remote PLCs.

PLCs require programming device which is used to develop and later download the created program into the memory of the controller.

Modern PLCs generally contain a real-time operating system, such as OS-9 or VxWorks.

Mechanical design

Compact PLC with 8 inputs and 4 outputs
Modular PLC with EtherNet/IP module, digital and analog I/O, with some slots being empty.
Modular PLC with EtherNet/IP module, discrete and analog I/O, with some slots being empty

There are two types of mechanical design for PLC systems. A single box, or a brick is a small programmable controller that fits all units and interfaces into one compact casing, although, typically, additional expansion modules for inputs and outputs are available. Second design type – a modular PLC – has a chassis (also called a rack) that provides space for modules with different functions, such as power supply, processor, selection of I/O modules and communication interfaces – which all can be customized for the particular application. Several racks can be administered by a single processor and may have thousands of inputs and outputs. Either a special high-speed serial I/O link or comparable communication method is used so that racks can be distributed away from the processor, reducing the wiring costs for large plants. Options are also available to mount I/O points directly to the machine and utilize quick disconnecting cables to sensors and valves, saving time for wiring and replacing components.

Discrete and analog signals

Discrete (digital) signals can only take on or off value (1 or 0, true or false). Examples of devices providing a discrete signal include limit switches, photoelectric sensors and encoders.

Analog signals can use voltage or current that is proportional to the size of the monitored variable and can take any value within their scale. Pressure, temperature, flow, and weight are often represented by analog signals. These are typically interpreted as integer values with various ranges of accuracy depending on the device and the number of bits available to store the data. For example, an analog 0 to 10 V or 4-20 mA current loop input would be converted into an integer value of 0 to 32,767. The PLC will take this value and transpose it into the desired units of the process so the operator or program can read it. Proper integration will also include filter times to reduce noise as well as high and low limits to report faults. Current inputs are less sensitive to electrical noise (e.g. from welders or electric motor starts) than voltage inputs. Distance from the device and the controller is also a concern as the maximum traveling distance of a good quality 0-10 V signal is very short compared to the 4-20 mA signal. The 4-20 mA signal can also report if the wire is disconnected along the path as a <4 mA signal would indicate an error.

Redundancy

Some special processes need to work permanently with minimum unwanted downtime. Therefore, it is necessary to design a system that is fault-tolerant and capable of handling the process with faulty modules. In such cases to increase the system availability in the event of hardware component failure, redundant CPU or I/O modules with the same functionality can be added to hardware configuration for preventing total or partial process shutdown due to hardware failure. Other redundancy scenarios could be related to safety-critical processes, for example, large hydraulic presses could require that both PLCs turn on output before the press can come down in case one output does not turn off properly.

Programming

Example of a ladder diagram logic

Programmable logic controllers are intended to be used by engineers without a programming background. For this reason, a graphical programming language called Ladder Diagram (LD, LAD) was first developed. It resembles the schematic diagram of a system built with electromechanical relays and was adopted by many manufacturers and later standardized in the IEC 61131-3 control systems programming standard. As of 2015, it is still widely used, thanks to its simplicity.

As of 2015, the majority of PLC systems adhere to the IEC 61131-3 standard that defines 2 textual programming languages: Structured Text (ST; similar to Pascal) and Instruction List (IL); as well as 3 graphical languages: Ladder Diagram, Function Block Diagram (FBD) and Sequential Function Chart (SFC). Instruction List (IL) was deprecated in the third edition of the standard.

Modern PLCs can be programmed in a variety of ways, from the relay-derived ladder logic to programming languages such as specially adapted dialects of BASIC and C.

While the fundamental concepts of PLC programming are common to all manufacturers, differences in I/O addressing, memory organization, and instruction sets mean that PLC programs are never perfectly interchangeable between different makers. Even within the same product line of a single manufacturer, different models may not be directly compatible.

Programming device

PLC programs are typically written in a programming device, which can take the form of a desktop console, special software on a personal computer, or a handheld programming device. Then, the program is downloaded to the PLC directly or over a network. It is stored either in non-volatile flash memory or battery-backed-up RAM. In some programmable controllers, the program is transferred from a personal computer to the PLC through a programming board that writes the program into a removable chip, such as EPROM.

Manufacturers develop programming software for their controllers. In addition to being able to program PLCs in multiple languages, they provide common features like hardware diagnostics and maintenance, software debugging, and offline simulation.

Simulation

PLC simulation is a feature often found in PLC programming software. It allows for testing and debugging early in a project's development.

Incorrectly programmed PLC can result in lost productivity and dangerous conditions. Testing the project in simulation improves its quality, increases the level of safety associated with equipment and can save costly downtime during the installation and commissioning of automated control applications since many scenarios can be tried and tested before the system is activated.

Functionality

PLC system in a rack, left-to-right: power supply unit (PSU), CPU, interface module (IM) and communication processor (CP)
Control panel with PLC (gray elements in the center). The unit consists of separate elements, from left to right: power supply, controller, relay units for input and output.

The main difference from most other computing devices is that PLCs are intended-for and therefore tolerant-of more severe conditions (such as dust, moisture, heat, cold), while offering extensive input/output (I/O) to connect the PLC to sensors and actuators. PLC input can include simple digital elements such as limit switches, analog variables from process sensors (such as temperature and pressure), and more complex data such as that from positioning or machine vision systems. PLC output can include elements such as indicator lamps, sirens, electric motors, pneumatic or hydraulic cylinders, magnetic relays, solenoids, or analog outputs. The input/output arrangements may be built into a simple PLC, or the PLC may have external I/O modules attached to a fieldbus or computer network that plugs into the PLC.

The functionality of the PLC has evolved over the years to include sequential relay control, motion control, process control, distributed control systems, and networking. The data handling, storage, processing power, and communication capabilities of some modern PLCs are approximately equivalent to desktop computers. PLC-like programming combined with remote I/O hardware, allows a general-purpose desktop computer to overlap some PLCs in certain applications. Desktop computer controllers have not been generally accepted in heavy industry because desktop computers run on less stable operating systems than PLCs, and because the desktop computer hardware is typically not designed to the same levels of tolerance to temperature, humidity, vibration, and longevity as the processors used in PLCs. Operating systems such as Windows do not lend themselves to deterministic logic execution, with the result that the controller may not always respond to changes of input status with the consistency in timing expected from PLCs. Desktop logic applications find use in less critical situations, such as laboratory automation and use in small facilities where the application is less demanding and critical.

Basic functions

The most basic function of a programmable controller is to emulate the functions of electromechanical relays. Discrete inputs are given a unique address, and a PLC instruction can test if the input state is on or off. Just as a series of relay contacts perform a logical AND function, not allowing current to pass unless all the contacts are closed, so a series of "examine if on" instructions will energize its output storage bit if all the input bits are on. Similarly, a parallel set of instructions will perform a logical OR. In an electromechanical relay wiring diagram, a group of contacts controlling one coil is called a "rung" of a "ladder diagram ", and this concept is also used to describe PLC logic. Some models of PLC limit the number of series and parallel instructions in one "rung" of logic. The output of each rung sets or clears a storage bit, which may be associated with a physical output address or which may be an "internal coil" with no physical connection. Such internal coils can be used, for example, as a common element in multiple separate rungs. Unlike physical relays, there is usually no limit to the number of times an input, output or internal coil can be referenced in a PLC program.

Some PLCs enforce a strict left-to-right, top-to-bottom execution order for evaluating the rung logic. This is different from electro-mechanical relay contacts, which, in a sufficiently complex circuit, may either pass current left-to-right or right-to-left, depending on the configuration of surrounding contacts. The elimination of these "sneak paths" is either a bug or a feature, depending on the programming style.

More advanced instructions of the PLC may be implemented as functional blocks, which carry out some operation when enabled by a logical input and which produce outputs to signal, for example, completion or errors, while manipulating variables internally that may not correspond to discrete logic.

Communication

PLCs use built-in ports, such as USB, Ethernet, RS-232, RS-485, or RS-422 to communicate with external devices (sensors, actuators) and systems (programming software, SCADA, HMI). Communication is carried over various industrial network protocols, like Modbus, or EtherNet/IP. Many of these protocols are vendor specific.

PLCs used in larger I/O systems may have peer-to-peer (P2P) communication between processors. This allows separate parts of a complex process to have individual control while allowing the subsystems to co-ordinate over the communication link. These communication links are also often used for HMI devices such as keypads or PC-type workstations.

Formerly, some manufacturers offered dedicated communication modules as an add-on function where the processor had no network connection built-in.

User interface

See also: User interface and List of human-computer interaction topics
Control panel with a PLC user interface for thermal oxidizer regulation

PLCs may need to interact with people for the purpose of configuration, alarm reporting, or everyday control. A human-machine interface (HMI) is employed for this purpose. HMIs are also referred to as man-machine interfaces (MMIs) and graphical user interfaces (GUIs). A simple system may use buttons and lights to interact with the user. Text displays are available as well as graphical touch screens. More complex systems use programming and monitoring software installed on a computer, with the PLC connected via a communication interface.

Process of a scan cycle

A PLC works in a program scan cycle, where it executes its program repeatedly. The simplest scan cycle consists of 3 steps:

  1. Read inputs.
  2. Execute the program.
  3. Write outputs.

The program follows the sequence of instructions. It typically takes a time span of tens of milliseconds for the processor to evaluate all the instructions and update the status of all outputs. If the system contains remote I/O—for example, an external rack with I/O modules—then that introduces additional uncertainty in the response time of the PLC system.

As PLCs became more advanced, methods were developed to change the sequence of ladder execution, and subroutines were implemented.

Special-purpose I/O modules may be used where the scan time of the PLC is too long to allow predictable performance. Precision timing modules, or counter modules for use with shaft encoders, are used where the scan time would be too long to reliably count pulses or detect the sense of rotation of an encoder. This allows even a relatively slow PLC to still interpret the counted values to control a machine, as the accumulation of pulses is done by a dedicated module that is unaffected by the speed of program execution.

Security

In his book from 1998, E. A. Parr pointed out that even though most programmable controllers require physical keys and passwords, the lack of strict access control and version control systems, as well as an easy-to-understand programming language make it likely that unauthorized changes to programs will happen and remain unnoticed.

Prior to the discovery of the Stuxnet computer worm in June 2010, the security of PLCs received little attention. Modern programmable controllers generally contain a real-time operating systems, which can be vulnerable to exploits in a similar way as desktop operating systems, like Microsoft Windows. PLCs can also be attacked by gaining control of a computer they communicate with. Since 2011, these concerns have grown as networking is becoming more commonplace in the PLC environment connecting the previously separate plant floor networks and office networks.

In February 2021, Rockwell Automation publicly disclosed a critical vulnerability affecting its Logix controllers family. Secret cryptographic key used to verify communication between the PLC and workstation can be extracted from Studio 5000 Logix Designer programming software and used to remotely change program code and configuration of connected controller. The vulnerability was given a severity score of 10 out of 10 on the CVSS vulnerability scale. At the time of writing, the mitigation of the vulnerability was to limit network access to affected devices.

Safety PLCs

Safety PLCs can be either a standalone model or a safety-rated hardware and functionality added to existing controller architectures (Allen-Bradley Guardlogix, Siemens F-series etc.). These differ from conventional PLC types by being suitable for safety-critical applications for which PLCs have traditionally been supplemented with hard-wired safety relays and areas of the memory dedicated to the safety instructions. The standard of safety level is the SIL.

A safety PLC might be used to control access to a robot cell with trapped-key access, or to manage the shutdown response to an emergency stop on a conveyor production line. Such PLCs typically have a restricted regular instruction set augmented with safety-specific instructions designed to interface with emergency stops, light screens, and so forth.

The flexibility that such systems offer has resulted in rapid growth of demand for these controllers.

PLC compared with other control systems

PLC installed in a control panel
Control center with a PLC for a RTO

PLCs are well adapted to a range of automation tasks. These are typically industrial processes in manufacturing where the cost of developing and maintaining the automation system is high relative to the total cost of the automation, and where changes to the system would be expected during its operational life. PLCs contain input and output devices compatible with industrial pilot devices and controls; little electrical design is required, and the design problem centers on expressing the desired sequence of operations. PLC applications are typically highly customized systems, so the cost of a packaged PLC is low compared to the cost of a specific custom-built controller design. On the other hand, in the case of mass-produced goods, customized control systems are economical. This is due to the lower cost of the components, which can be optimally chosen instead of a "generic" solution, and where the non-recurring engineering charges are spread over thousands or millions of units.

Programmable controllers are widely used in motion, positioning, or torque control. Some manufacturers produce motion control units to be integrated with PLC so that G-code (involving a CNC machine) can be used to instruct machine movements.

PLC Chip / Embedded Controller

Nano ACE PLC & Chip PLC for small machine builders / small or medium volumes

For small machines with low or medium volume. PLCs that can execute PLC languages such as Ladder, Flow-Chart/Grafcet,... Similar to traditional PLCs, but their small size allows developers to design them into custom printed circuit boards like a microcontroller, without computer programming knowledge, but with a language that is easy to use, modify and maintain. It is between the classic PLC / Micro-PLC and the Microcontrollers.

Microcontrollers

A microcontroller-based design would be appropriate where hundreds or thousands of units will be produced and so the development cost (design of power supplies, input/output hardware, and necessary testing and certification) can be spread over many sales, and where the end-user would not need to alter the control. Automotive applications are an example; millions of units are built each year, and very few end-users alter the programming of these controllers. However, some specialty vehicles such as transit buses economically use PLCs instead of custom-designed controls, because the volumes are low and the development cost would be uneconomical.

Single-board computers

Very complex process control, such as those used in the chemical industry, may require algorithms and performance beyond the capability of even high-performance PLCs. Very high-speed or precision controls may also require customized solutions; for example, aircraft flight controls. Single-board computers using semi-customized or fully proprietary hardware may be chosen for very demanding control applications where the high development and maintenance cost can be supported. "Soft PLCs" running on desktop-type computers can interface with industrial I/O hardware while executing programs within a version of commercial operating systems adapted for process control needs.

The rising popularity of single board computers has also had an influence on the development of PLCs. Traditional PLCs are generally closed platforms, but some newer PLCs (e.g. groov EPIC from Opto 22, ctrlX from Bosch Rexroth, PFC200 from Wago, PLCnext from Phoenix Contact, and Revolution Pi from Kunbus) provide the features of traditional PLCs on an open platform.

Programmable logic relays (PLR)

In more recent years, small products called programmable logic relays (PLRs) or smart relays, have become more common and accepted. These are similar to PLCs and are used in light industries where only a few points of I/O are needed, and low cost is desired. These small devices are typically made in a common physical size and shape by several manufacturers and branded by the makers of larger PLCs to fill their low-end product range. Most of these have 8 to 12 discrete inputs, 4 to 8 discrete outputs, and up to 2 analog inputs. Most such devices include a tiny postage-stamp-sized LCD screen for viewing simplified ladder logic (only a very small portion of the program being visible at a given time) and status of I/O points, and typically these screens are accompanied by a 4-way rocker push-button plus four more separate push-buttons, similar to the key buttons on a VCR remote control, and used to navigate and edit the logic. Most have a small plug for connecting via RS-232 or RS-485 to a personal computer so that programmers can use simple applications in general-purpose OS like MS Windows, macOS or Linux, that have user-friendly (G)UIs, for programming instead of being forced to use the tiny LCD and push-button set for this purpose. Unlike regular PLCs that are usually modular and greatly expandable, the PLRs are usually not modular or expandable, but their price can be two orders of magnitude less than a PLC, and they still offer robust design and deterministic execution of the logic.

A variant of PLCs, used in remote locations is the remote terminal unit or RTU. An RTU is typically a low power, ruggedized PLC whose key function is to manage the communications links between the site and the central control system (typically SCADA) or in some modern systems, "The Cloud". Unlike factory automation using high-speed Ethernet, communications links to remote sites are often radio-based and are less reliable. To account for the reduced reliability, RTU will buffer messages or switch to alternate communications paths. When buffering messages, the RTU will timestamp each message so that a full history of site events can be reconstructed. RTUs, being PLCs, have a wide range of I/O and are fully programmable, typically with languages from the IEC 61131-3 standard that is common to many PLCs, RTUs and DCSs. In remote locations, it is common to use an RTU as a gateway for a PLC, where the PLC is performing all site control and the RTU is managing communications, time-stamping events and monitoring ancillary equipment. On sites with only a handful of I/O, the RTU may also be the site PLC and will perform both communications and control functions.

at
Subscribe to: Posts (Atom)

Introduction to entropy

From Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Introduct...

  • Islamic State and the Levant
    From Wikipedia, the free encyclopedia Islamic State of Iraq and the Levant الدولة الإسلامية في العراق والشام   ( ...
  • Heart Sutra
    From Wikipedia, the free encyclopedia A reproduction of the palm -leaf manuscript in Siddham script ...
  • Slum
    From Wikipedia, the free encyclopedia ...