Linear programming

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Linear_programming

 

For the retronym referring to television broadcasting, see Broadcast programming.

A pictorial representation of a simple linear program with two variables and six inequalities. The set of feasible solutions is depicted in yellow and forms a polygon, a 2-dimensional polytope. The optimum of the linear cost function is where the red line intersects the polygon. The red line is a level set of the cost function, and the arrow indicates the direction in which we are optimizing.

A closed feasible region of a problem with three variables is a convex polyhedron. The surfaces giving a fixed value of the objective function are planes (not shown). The linear programming problem is to find a point on the polyhedron that is on the plane with the highest possible value.

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization).

More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polytope, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where this function has the largest (or smallest) value if such a point exists.

Linear programs are problems that can be expressed in standard form as

${\displaystyle \begin{array}{rlrl}& \text{Find a vector}& & \mathbf{x}\\ & \text{that maximizes}& & {\mathbf{c}}^{\mathsf{T}}\mathbf{x}\\ & \text{subject to}& & A\mathbf{x}\le \mathbf{b}\\ & \text{and}& & \mathbf{x}\ge \mathbf{0}.\end{array}}$

Here the components of ${\displaystyle \mathbf{x}}$ are the variables to be determined, ${\displaystyle \mathbf{c}}$ and ${\displaystyle \mathbf{b}}$ are given vectors, and ${\displaystyle A}$ is a given matrix. The function whose value is to be maximized (${\displaystyle \mathbf{x}\mapsto {\mathbf{c}}^{\mathsf{T}}\mathbf{x}}$ in this case) is called the objective function. The constraints ${\displaystyle A\mathbf{x}\le \mathbf{b}}$ and ${\displaystyle \mathbf{x}\ge \mathbf{0}}$ specify a convex polytope over which the objective function is to be optimized.

Linear programming can be applied to various fields of study. It is widely used in mathematics and, to a lesser extent, in business, economics, and some engineering problems. Industries that use linear programming models include transportation, energy, telecommunications, and manufacturing. It has proven useful in modeling diverse types of problems in planning, routing, scheduling, assignment, and design.

History

Leonid Kantorovich

John von Neumann

The problem of solving a system of linear inequalities dates back at least as far as Fourier, who in 1827 published a method for solving them, and after whom the method of Fourier–Motzkin elimination is named.

In the late 1930s, Soviet mathematician Leonid Kantorovich and American economist Wassily Leontief independently delved into the practical applications of linear programming. Kantorovich focused on manufacturing schedules, while Leontief explored economic applications. Their groundbreaking work was largely overlooked for decades.

The turning point came during World War II when linear programming emerged as a vital tool. It found extensive use in addressing complex wartime challenges, including transportation logistics, scheduling, and resource allocation. Linear programming proved invaluable in optimizing these processes while considering critical constraints such as costs and resource availability.

Despite its initial obscurity, the wartime successes propelled linear programming into the spotlight. Post-WWII, the method gained widespread recognition and became a cornerstone in various fields, from operations research to economics. The overlooked contributions of Kantorovich and Leontief in the late 1930s eventually became foundational to the broader acceptance and utilization of linear programming in optimizing decision-making processes.

Kantorovich's work was initially neglected in the USSR. About the same time as Kantorovich, the Dutch-American economist T. C. Koopmans formulated classical economic problems as linear programs. Kantorovich and Koopmans later shared the 1975 Nobel prize in economics. In 1941, Frank Lauren Hitchcock also formulated transportation problems as linear programs and gave a solution very similar to the later simplex method. Hitchcock had died in 1957, and the Nobel prize is not awarded posthumously.

From 1946 to 1947 George B. Dantzig independently developed general linear programming formulation to use for planning problems in the US Air Force. In 1947, Dantzig also invented the simplex method that, for the first time efficiently, tackled the linear programming problem in most cases. When Dantzig arranged a meeting with John von Neumann to discuss his simplex method, Neumann immediately conjectured the theory of duality by realizing that the problem he had been working in game theory was equivalent. Dantzig provided formal proof in an unpublished report "A Theorem on Linear Inequalities" on January 5, 1948. Dantzig's work was made available to public in 1951. In the post-war years, many industries applied it in their daily planning.

Dantzig's original example was to find the best assignment of 70 people to 70 jobs. The computing power required to test all the permutations to select the best assignment is vast; the number of possible configurations exceeds the number of particles in the observable universe. However, it takes only a moment to find the optimum solution by posing the problem as a linear program and applying the simplex algorithm. The theory behind linear programming drastically reduces the number of possible solutions that must be checked.

The linear programming problem was first shown to be solvable in polynomial time by Leonid Khachiyan in 1979, but a larger theoretical and practical breakthrough in the field came in 1984 when Narendra Karmarkar introduced a new interior-point method for solving linear-programming problems.

Uses

Linear programming is a widely used field of optimization for several reasons. Many practical problems in operations research can be expressed as linear programming problems. Certain special cases of linear programming, such as network flow problems and multicommodity flow problems, are considered important enough to have much research on specialized algorithms. A number of algorithms for other types of optimization problems work by solving linear programming problems as sub-problems. Historically, ideas from linear programming have inspired many of the central concepts of optimization theory, such as duality, decomposition, and the importance of convexity and its generalizations. Likewise, linear programming was heavily used in the early formation of microeconomics, and it is currently utilized in company management, such as planning, production, transportation, and technology. Although the modern management issues are ever-changing, most companies would like to maximize profits and minimize costs with limited resources. Google also uses linear programming to stabilize YouTube videos.

Standard form

Standard form is the usual and most intuitive form of describing a linear programming problem. It consists of the following three parts:

• A linear (or affine) function to be maximized

e.g. ${\displaystyle f(x_1,x_2)=c_1{x}_1+c_2{x}_2}$

• Problem constraints of the following form

e.g.

${\displaystyle \begin{array}{cc}{a}_{11}{x}_1+a_{12}{x}_2& \le b_1\\ a_{21}{x}_1+a_{22}{x}_2& \le b_2\\ a_{31}{x}_1+a_{32}{x}_2& \le b_3\end{array}}$

• Non-negative variables

e.g.

${\displaystyle \begin{array}{c}{x}_1\ge 0\\ x_2\ge 0\end{array}}$

The problem is usually expressed in matrix form, and then becomes:

${\displaystyle max\{{\mathbf{c}}^{\mathsf{T}}\mathbf{x}\mid \mathbf{x}\in {\mathbb{R}}^n\wedge A\mathbf{x}\le \mathbf{b}\wedge \mathbf{x}\ge 0\}}$

Other forms, such as minimization problems, problems with constraints on alternative forms, and problems involving negative variables can always be rewritten into an equivalent problem in standard form.

Example

Graphical solution to the farmer example – after shading regions violating the conditions, the vertex of the unshaded region with the dashed line farthest from the origin gives the optimal combination (its lying on the pesticide and land lines implies that pesticide and land limit revenue)

Suppose that a farmer has a piece of farm land, say L km², to be planted with either wheat or barley or some combination of the two. The farmer has a limited amount of fertilizer, F kilograms, and pesticide, P kilograms. Every square kilometer of wheat requires F₁ kilograms of fertilizer and P₁ kilograms of pesticide, while every square kilometer of barley requires F₂ kilograms of fertilizer and P₂ kilograms of pesticide. Let S₁ be the selling price of wheat per square kilometer, and S₂ be the selling price of barley. If we denote the area of land planted with wheat and barley by x₁ and x₂ respectively, then profit can be maximized by choosing optimal values for x₁ and x₂. This problem can be expressed with the following linear programming problem in the standard form:

Maximize: ${\displaystyle S_1\cdot x_1+S_2\cdot x_2}$		(maximize the revenue (the total wheat sales plus the total barley sales) – revenue is the "objective function")
Subject to:	${\displaystyle x_1+x_2\le L}$	(limit on total area)
	${\displaystyle F_1\cdot x_1+F_2\cdot x_2\le F}$	(limit on fertilizer)
	${\displaystyle P_1\cdot x_1+P_2\cdot x_2\le P}$	(limit on pesticide)
	${\displaystyle x_1\ge 0,x_2\ge 0}$	(cannot plant a negative area).

In matrix form this becomes:

maximize ${\displaystyle \left[\begin{array}{cc}{S}_1& S_2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]}$

subject to ${\displaystyle \left[\begin{array}{cc}1& 1\\ F_1& F_2\\ P_1& P_2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\le \left[\begin{array}{c}L\\ F\\ P\end{array}\right],\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\ge \left[\begin{array}{c}0\\ 0\end{array}\right].}$

Augmented form (slack form)

Linear programming problems can be converted into an augmented form in order to apply the common form of the simplex algorithm. This form introduces non-negative slack variables to replace inequalities with equalities in the constraints. The problems can then be written in the following block matrix form:

Maximize ${\displaystyle z}$:

${\displaystyle \left[\begin{array}{ccc}1& -{\mathbf{c}}^{\mathsf{T}}& 0\\ 0& \mathbf{A}& \mathbf{I}\end{array}\right]\left[\begin{array}{c}z\\ \mathbf{x}\\ \mathbf{s}\end{array}\right]=\left[\begin{array}{c}0\\ \mathbf{b}\end{array}\right]}$

${\displaystyle \mathbf{x}\ge 0,\mathbf{s}\ge 0}$

where ${\displaystyle \mathbf{s}}$ are the newly introduced slack variables, ${\displaystyle \mathbf{x}}$ are the decision variables, and ${\displaystyle z}$ is the variable to be maximized.

Example

The example above is converted into the following augmented form:

Maximize: ${\displaystyle S_1\cdot x_1+S_2\cdot x_2}$		(objective function)
subject to:	${\displaystyle x_1+x_2+x_3=L}$	(augmented constraint)
	${\displaystyle F_1\cdot x_1+F_2\cdot x_2+x_4=F}$	(augmented constraint)
	${\displaystyle P_1\cdot x_1+P_2\cdot x_2+x_5=P}$	(augmented constraint)
	${\displaystyle x_1,x_2,x_3,x_4,x_5\ge 0.}$

where ${\displaystyle x_3,x_4,x_5}$ are (non-negative) slack variables, representing in this example the unused area, the amount of unused fertilizer, and the amount of unused pesticide.

In matrix form this becomes:

Maximize ${\displaystyle z}$:

$${\displaystyle \left[\begin{array}{cccccc}1& -S_1& -S_2& 0& 0& 0\\ 0& 1& 1& 1& 0& 0\\ 0& F_1& F_2& 0& 1& 0\\ 0& P_1& P_2& 0& 0& 1\end{array}\right]\left[\begin{array}{c}z\\ x_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]=\left[\begin{array}{c}0\\ L\\ F\\ P\end{array}\right],\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]\ge 0.}$$

Duality

Main article: Dual linear program

Every linear programming problem, referred to as a primal problem, can be converted into a dual problem, which provides an upper bound to the optimal value of the primal problem. In matrix form, we can express the primal problem as:

Maximize c^Tx subject to Ax ≤ b, x ≥ 0;

with the corresponding symmetric dual problem,

Minimize b^Ty subject to A^Ty ≥ c, y ≥ 0.

An alternative primal formulation is:

Maximize c^Tx subject to Ax ≤ b;

with the corresponding asymmetric dual problem,

Minimize b^Ty subject to A^Ty = c, y ≥ 0.

There are two ideas fundamental to duality theory. One is the fact that (for the symmetric dual) the dual of a dual linear program is the original primal linear program. Additionally, every feasible solution for a linear program gives a bound on the optimal value of the objective function of its dual. The weak duality theorem states that the objective function value of the dual at any feasible solution is always greater than or equal to the objective function value of the primal at any feasible solution. The strong duality theorem states that if the primal has an optimal solution, x^*, then the dual also has an optimal solution, y^*, and c^Tx^*=b^Ty^*.

A linear program can also be unbounded or infeasible. Duality theory tells us that if the primal is unbounded then the dual is infeasible by the weak duality theorem. Likewise, if the dual is unbounded, then the primal must be infeasible. However, it is possible for both the dual and the primal to be infeasible. See dual linear program for details and several more examples.

Variations

Covering/packing dualities

Covering/packing-problem pairs
Covering problems Packing problems Minimum set cover Maximum set packing Minimum edge cover Maximum matching Minimum vertex cover Maximum independent set Bin covering Bin packing Polygon covering Rectangle packing

A covering LP is a linear program of the form:

Minimize: b^Ty,

subject to: A^Ty ≥ c, y ≥ 0,

such that the matrix A and the vectors b and c are non-negative.

The dual of a covering LP is a packing LP, a linear program of the form:

Maximize: c^Tx,

subject to: Ax ≤ b, x ≥ 0,

such that the matrix A and the vectors b and c are non-negative.

Examples

Covering and packing LPs commonly arise as a linear programming relaxation of a combinatorial problem and are important in the study of approximation algorithms. For example, the LP relaxations of the set packing problem, the independent set problem, and the matching problem are packing LPs. The LP relaxations of the set cover problem, the vertex cover problem, and the dominating set problem are also covering LPs.

Finding a fractional coloring of a graph is another example of a covering LP. In this case, there is one constraint for each vertex of the graph and one variable for each independent set of the graph.

Complementary slackness

It is possible to obtain an optimal solution to the dual when only an optimal solution to the primal is known using the complementary slackness theorem. The theorem states:

Suppose that x = (x₁, x₂, ... , x_n) is primal feasible and that y = (y₁, y₂, ... , y_m) is dual feasible. Let (w₁, w₂, ..., w_m) denote the corresponding primal slack variables, and let (z₁, z₂, ... , z_n) denote the corresponding dual slack variables. Then x and y are optimal for their respective problems if and only if

• x_j z_j = 0, for j = 1, 2, ... , n, and
• w_i y_i = 0, for i = 1, 2, ... , m.

So if the i-th slack variable of the primal is not zero, then the i-th variable of the dual is equal to zero. Likewise, if the j-th slack variable of the dual is not zero, then the j-th variable of the primal is equal to zero.

This necessary condition for optimality conveys a fairly simple economic principle. In standard form (when maximizing), if there is slack in a constrained primal resource (i.e., there are "leftovers"), then additional quantities of that resource must have no value. Likewise, if there is slack in the dual (shadow) price non-negativity constraint requirement, i.e., the price is not zero, then there must be scarce supplies (no "leftovers").

Theory

Existence of optimal solutions

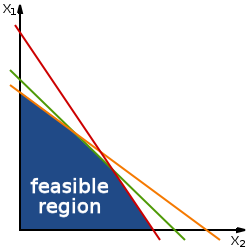
Geometrically, the linear constraints define the feasible region, which is a convex polytope. A linear function is a convex function, which implies that every local minimum is a global minimum; similarly, a linear function is a concave function, which implies that every local maximum is a global maximum.

An optimal solution need not exist, for two reasons. First, if the constraints are inconsistent, then no feasible solution exists: For instance, the constraints x ≥ 2 and x ≤ 1 cannot be satisfied jointly; in this case, we say that the LP is infeasible. Second, when the polytope is unbounded in the direction of the gradient of the objective function (where the gradient of the objective function is the vector of the coefficients of the objective function), then no optimal value is attained because it is always possible to do better than any finite value of the objective function.

Optimal vertices (and rays) of polyhedra

Otherwise, if a feasible solution exists and if the constraint set is bounded, then the optimum value is always attained on the boundary of the constraint set, by the maximum principle for convex functions (alternatively, by the minimum principle for concave functions) since linear functions are both convex and concave. However, some problems have distinct optimal solutions; for example, the problem of finding a feasible solution to a system of linear inequalities is a linear programming problem in which the objective function is the zero function (i.e., the constant function taking the value zero everywhere). For this feasibility problem with the zero-function for its objective-function, if there are two distinct solutions, then every convex combination of the solutions is a solution.

The vertices of the polytope are also called basic feasible solutions. The reason for this choice of name is as follows. Let d denote the number of variables. Then the fundamental theorem of linear inequalities implies (for feasible problems) that for every vertex x^* of the LP feasible region, there exists a set of d (or fewer) inequality constraints from the LP such that, when we treat those d constraints as equalities, the unique solution is x^*. Thereby we can study these vertices by means of looking at certain subsets of the set of all constraints (a discrete set), rather than the continuum of LP solutions. This principle underlies the simplex algorithm for solving linear programs.

Algorithms

See also: List of numerical analysis topics § Linear programming

In a linear programming problem, a series of linear constraints produces a convex feasible region of possible values for those variables. In the two-variable case this region is in the shape of a convex simple polygon.

Basis exchange algorithms

Simplex algorithm of Dantzig

The simplex algorithm, developed by George Dantzig in 1947, solves LP problems by constructing a feasible solution at a vertex of the polytope and then walking along a path on the edges of the polytope to vertices with non-decreasing values of the objective function until an optimum is reached for sure. In many practical problems, "stalling" occurs: many pivots are made with no increase in the objective function. In rare practical problems, the usual versions of the simplex algorithm may actually "cycle". To avoid cycles, researchers developed new pivoting rules.

In practice, the simplex algorithm is quite efficient and can be guaranteed to find the global optimum if certain precautions against cycling are taken. The simplex algorithm has been proved to solve "random" problems efficiently, i.e. in a cubic number of steps, which is similar to its behavior on practical problems.

However, the simplex algorithm has poor worst-case behavior: Klee and Minty constructed a family of linear programming problems for which the simplex method takes a number of steps exponential in the problem size. In fact, for some time it was not known whether the linear programming problem was solvable in polynomial time, i.e. of complexity class P.

Criss-cross algorithm

Like the simplex algorithm of Dantzig, the criss-cross algorithm is a basis-exchange algorithm that pivots between bases. However, the criss-cross algorithm need not maintain feasibility, but can pivot rather from a feasible basis to an infeasible basis. The criss-cross algorithm does not have polynomial time-complexity for linear programming. Both algorithms visit all 2^D corners of a (perturbed) cube in dimension D, the Klee–Minty cube, in the worst case.

Interior point

In contrast to the simplex algorithm, which finds an optimal solution by traversing the edges between vertices on a polyhedral set, interior-point methods move through the interior of the feasible region.

Ellipsoid algorithm, following Khachiyan

This is the first worst-case polynomial-time algorithm ever found for linear programming. To solve a problem which has n variables and can be encoded in L input bits, this algorithm runs in ${\displaystyle O(n^{6}L)}$ time. Leonid Khachiyan solved this long-standing complexity issue in 1979 with the introduction of the ellipsoid method. The convergence analysis has (real-number) predecessors, notably the iterative methods developed by Naum Z. Shor and the approximation algorithms by Arkadi Nemirovski and D. Yudin.

Projective algorithm of Karmarkar

Main article: Karmarkar's algorithm

Khachiyan's algorithm was of landmark importance for establishing the polynomial-time solvability of linear programs. The algorithm was not a computational break-through, as the simplex method is more efficient for all but specially constructed families of linear programs.

However, Khachiyan's algorithm inspired new lines of research in linear programming. In 1984, N. Karmarkar proposed a projective method for linear programming. Karmarkar's algorithm improved on Khachiyan's worst-case polynomial bound (giving ${\displaystyle O(n^{3.5}L)}$). Karmarkar claimed that his algorithm was much faster in practical LP than the simplex method, a claim that created great interest in interior-point methods. Since Karmarkar's discovery, many interior-point methods have been proposed and analyzed.

Vaidya's 87 algorithm

In 1987, Vaidya proposed an algorithm that runs in ${\displaystyle O(n^3)}$ time.

Vaidya's 89 algorithm

In 1989, Vaidya developed an algorithm that runs in ${\displaystyle O(n^{2.5})}$ time. Formally speaking, the algorithm takes ${\displaystyle O((n+d{)}^{1.5}nL)}$ arithmetic operations in the worst case, where ${\displaystyle d}$ is the number of constraints, ${\displaystyle n}$ is the number of variables, and ${\displaystyle L}$ is the number of bits.

Input sparsity time algorithms

In 2015, Lee and Sidford showed that, it can be solved in ${\displaystyle \tilde{O}((nnz(A)+d^2)\sqrt{d}L)}$ time, where ${\displaystyle nnz(A)}$ represents the number of non-zero elements, and it remains taking ${\displaystyle O(n^{2.5}L)}$ in the worst case.

Current matrix multiplication time algorithm

In 2019, Cohen, Lee and Song improved the running time to ${\displaystyle \tilde{O}((n^{\omega }+n^{2.5-\alpha /2}+n^{2+1/6})L)}$ time, ${\displaystyle \omega }$ is the exponent of matrix multiplication and ${\displaystyle \alpha }$ is the dual exponent of matrix multiplication. ${\displaystyle \alpha }$ is (roughly) defined to be the largest number such that one can multiply an ${\displaystyle n\times n}$ matrix by a ${\displaystyle n\times n^{\alpha }}$ matrix in ${\displaystyle O(n^2)}$ time. In a followup work by Lee, Song and Zhang, they reproduce the same result via a different method. These two algorithms remain ${\displaystyle \tilde{O}(n^{2+1/6}L)}$ when ${\displaystyle \omega =2}$ and ${\displaystyle \alpha =1}$. The result due to Jiang, Song, Weinstein and Zhang improved ${\displaystyle \tilde{O}(n^{2+1/6}L)}$ to ${\displaystyle \tilde{O}(n^{2+1/18}L)}$.

Comparison of interior-point methods and simplex algorithms

The current opinion is that the efficiencies of good implementations of simplex-based methods and interior point methods are similar for routine applications of linear programming. However, for specific types of LP problems, it may be that one type of solver is better than another (sometimes much better), and that the structure of the solutions generated by interior point methods versus simplex-based methods are significantly different with the support set of active variables being typically smaller for the latter one.

Open problems and recent work

Unsolved problem in computer science:

Does linear programming admit a strongly polynomial-time algorithm?

There are several open problems in the theory of linear programming, the solution of which would represent fundamental breakthroughs in mathematics and potentially major advances in our ability to solve large-scale linear programs.

• Does LP admit a strongly polynomial-time algorithm?
• Does LP admit a strongly polynomial-time algorithm to find a strictly complementary solution?
• Does LP admit a polynomial-time algorithm in the real number (unit cost) model of computation?

This closely related set of problems has been cited by Stephen Smale as among the 18 greatest unsolved problems of the 21st century. In Smale's words, the third version of the problem "is the main unsolved problem of linear programming theory." While algorithms exist to solve linear programming in weakly polynomial time, such as the ellipsoid methods and interior-point techniques, no algorithms have yet been found that allow strongly polynomial-time performance in the number of constraints and the number of variables. The development of such algorithms would be of great theoretical interest, and perhaps allow practical gains in solving large LPs as well.

Although the Hirsch conjecture was recently disproved for higher dimensions, it still leaves the following questions open.

• Are there pivot rules which lead to polynomial-time simplex variants?
• Do all polytopal graphs have polynomially bounded diameter?

These questions relate to the performance analysis and development of simplex-like methods. The immense efficiency of the simplex algorithm in practice despite its exponential-time theoretical performance hints that there may be variations of simplex that run in polynomial or even strongly polynomial time. It would be of great practical and theoretical significance to know whether any such variants exist, particularly as an approach to deciding if LP can be solved in strongly polynomial time.

The simplex algorithm and its variants fall in the family of edge-following algorithms, so named because they solve linear programming problems by moving from vertex to vertex along edges of a polytope. This means that their theoretical performance is limited by the maximum number of edges between any two vertices on the LP polytope. As a result, we are interested in knowing the maximum graph-theoretical diameter of polytopal graphs. It has been proved that all polytopes have subexponential diameter. The recent disproof of the Hirsch conjecture is the first step to prove whether any polytope has superpolynomial diameter. If any such polytopes exist, then no edge-following variant can run in polynomial time. Questions about polytope diameter are of independent mathematical interest.

Simplex pivot methods preserve primal (or dual) feasibility. On the other hand, criss-cross pivot methods do not preserve (primal or dual) feasibility – they may visit primal feasible, dual feasible or primal-and-dual infeasible bases in any order. Pivot methods of this type have been studied since the 1970s. Essentially, these methods attempt to find the shortest pivot path on the arrangement polytope under the linear programming problem. In contrast to polytopal graphs, graphs of arrangement polytopes are known to have small diameter, allowing the possibility of strongly polynomial-time criss-cross pivot algorithm without resolving questions about the diameter of general polytopes.

Integer unknowns

If all of the unknown variables are required to be integers, then the problem is called an integer programming (IP) or integer linear programming (ILP) problem. In contrast to linear programming, which can be solved efficiently in the worst case, integer programming problems are in many practical situations (those with bounded variables) NP-hard. 0–1 integer programming or binary integer programming (BIP) is the special case of integer programming where variables are required to be 0 or 1 (rather than arbitrary integers). This problem is also classified as NP-hard, and in fact the decision version was one of Karp's 21 NP-complete problems.

If only some of the unknown variables are required to be integers, then the problem is called a mixed integer (linear) programming (MIP or MILP) problem. These are generally also NP-hard because they are even more general than ILP programs.

There are however some important subclasses of IP and MIP problems that are efficiently solvable, most notably problems where the constraint matrix is totally unimodular and the right-hand sides of the constraints are integers or – more general – where the system has the total dual integrality (TDI) property.

Advanced algorithms for solving integer linear programs include:

• cutting-plane method
• Branch and bound
• Branch and cut
• Branch and price
• if the problem has some extra structure, it may be possible to apply delayed column generation.

Such integer-programming algorithms are discussed by Padberg and in Beasley.

Integral linear programs

Further information: Integral polytope

A linear program in real variables is said to be integral if it has at least one optimal solution which is integral, i.e., made of only integer values. Likewise, a polyhedron ${\displaystyle P=\{x\mid Ax\ge 0\}}$ is said to be integral if for all bounded feasible objective functions c, the linear program ${\displaystyle \{maxcx\mid x\in P\}}$ has an optimum ${\displaystyle x^{\ast }}$ with integer coordinates. As observed by Edmonds and Giles in 1977, one can equivalently say that the polyhedron ${\displaystyle P}$ is integral if for every bounded feasible integral objective function c, the optimal value of the linear program ${\displaystyle \{maxcx\mid x\in P\}}$ is an integer.

Integral linear programs are of central importance in the polyhedral aspect of combinatorial optimization since they provide an alternate characterization of a problem. Specifically, for any problem, the convex hull of the solutions is an integral polyhedron; if this polyhedron has a nice/compact description, then we can efficiently find the optimal feasible solution under any linear objective. Conversely, if we can prove that a linear programming relaxation is integral, then it is the desired description of the convex hull of feasible (integral) solutions.

Terminology is not consistent throughout the literature, so one should be careful to distinguish the following two concepts,

• in an integer linear program, described in the previous section, variables are forcibly constrained to be integers, and this problem is NP-hard in general,
• in an integral linear program, described in this section, variables are not constrained to be integers but rather one has proven somehow that the continuous problem always has an integral optimal value (assuming c is integral), and this optimal value may be found efficiently since all polynomial-size linear programs can be solved in polynomial time.

One common way of proving that a polyhedron is integral is to show that it is totally unimodular. There are other general methods including the integer decomposition property and total dual integrality. Other specific well-known integral LPs include the matching polytope, lattice polyhedra, submodular flow polyhedra, and the intersection of two generalized polymatroids/g-polymatroids – e.g. see Schrijver 2003.

Power system simulation

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Power_system_simulation

Electrical power system simulation involves power system modeling and network simulation in order to analyze electrical power systems using design/offline or real-time data. Power system simulation software's are a class of computer simulation programs that focus on the operation of electrical power systems. These types of computer programs are used in a wide range of planning and operational situations for electric power systems.

Applications of power system simulation include: long-term generation and transmission expansion planning, short-term operational simulations, and market analysis (e.g. price forecasting). These programs typically make use of mathematical optimization techniques such linear programming, quadratic programming, and mixed integer programming.

Multiple elements of a power system can be modelled. A power-flow study calculates the loading on transmission lines and the power necessary to be generated at generating stations, given the required loads to be served. A short circuit study or fault analysis calculates the short-circuit current that would flow at various points of interest in the system under study, for short-circuits between phases or from energized wires to ground. A coordination study allows selection and setting of protective relays and fuses to rapidly clear a short-circuit fault while minimizing effects on the rest of the power system. Transient or dynamic stability studies show the effect of events such as sudden load changes, short-circuits, or accidental disconnection of load on the synchronization of the generators in the system. Harmonic or power quality studies show the effect of non-linear loads such as lighting on the waveform of the power system, and allow recommendations to be made to mitigate severe distortion. An optimal power-flow study establishes the best combination of generating plant output to meet a given load requirement, so as to minimize production cost while maintaining desired stability and reliability; such models may be updated in near-real-time to allow guidance to system operators on the lowest-cost way to achieve economic dispatch.

There are many power simulation software packages in commercial and non-commercial forms that range from utility-scale software to study tools.

Load flow calculation

The load-flow calculation is the most common network analysis tool for examining the undisturbed and disturbed network within the scope of operational and strategic planning.

Using network topology, transmission line parameters, transformer parameters, generator location and limits, and load location and compensation, the load-flow calculation can provide voltage magnitudes and angles for all nodes and loading of network components, such as cables and transformers. With this information, compliance to operating limitations such as those stipulated by voltage ranges and maximum loads, can be examined. This is, for example, important for determining the transmission capacity of underground cables, where the influence of cable bundling on the load capability of each cable has to be taken also into account.

Due to the ability to determine losses and reactive-power allocation, load-flow calculation also supports the planning engineer in the investigation of the most economical operation mode of the network.

When changing over from single and/or multi-phase infeed low-voltage meshed networks to isolated networks, load-flow calculation is essential for operational and economical reasons. Load-flow calculation is also the basis of all further network studies, such as motor start-up or investigation of scheduled or unscheduled outages of equipment within the outage simulation.

Especially when investigating motor start-up, the load-flow calculation results give helpful hints, for example, of whether the motor can be started in spite of the voltage drop caused by the start-up current.

Short circuit analysis

Short circuit analysis analyzes the power flow after a fault occurs in a power network. The faults may be three-phase short circuit, one-phase grounded, two-phase short circuit, two-phase grounded, one-phase break, two-phase break or complex faults. Results of such an analysis may help determine the following:

1. Magnitude of the fault current
2. Circuit breaker capacity
3. Rise in voltage in a single line due to ground fault
4. Residual voltage and relay settings
5. Interference due to power line.

Transient stability simulation

The goal of transient stability simulation of power systems is to analyse the stability of a power system from sub-second to several tens of seconds. Stability in this aspect is the ability of the system to quickly return to a stable operating condition after being exposed to a disturbance such as for example a tree falling over an overhead line resulting in the automatic disconnection of that line by its protection systems. In engineering terms, a power system is deemed stable if the substation voltage levels and the rotational speeds of motors and generators return to their normal values in a quick and continuous manner.

Figure 1. Specifies the acceptable amount of time it takes grid voltages return to their intended levels, which may vary depending on the magnitude of voltage disturbance.

Models typically use the following inputs:

• Number, size and type of generators with any available mechanical, electrical, and control (governor, voltage regulation, etc.) parameters,
• a mix of residential, commercial and industrial load at each bus,
• location and specifications for distributed control devices such as tap-changing transformers, switched shunt compensation, static Var compensators, flexible AC transmission systems, etc.,
• location and specifications for protection devices such as relays and load shedding, and
• location and specifications of any other relevant control and/or protection devices.

The acceptable amount of time it takes grid voltages return to their intended levels is dependent on the magnitude of voltage disturbance, and the most common standard is specified by the CBEMA curve in Figure. 1. This curve informs both electronic equipment design and grid stability data reporting.

Unit commitment

Main article: Unit commitment problem in electrical power production

The problem of unit commitment involves finding the least-cost dispatch of available generation resources to meet the electrical load.

Generating resources can include a wide range of types:

1. Nuclear
2. Thermal (using coal, gas, other fossil fuels, or biomass)
3. Renewables (including hydro, wind, wave-power, and solar)

The key decision variables that are decided by the computer program are:

1. Generation level (in megawatts)
2. Number of generating units on

The latter decisions are binary {0,1}, which means that the mathematical problem is not continuous.

In addition, generating plants are subject to a number of complex technical constraints, including:

1. Minimum stable operating level
2. Maximum rate of ramping up or down
3. Minimum time period the unit is up and/or down

These constraints have many different variants; all this gives rise to a large class of mathematical optimization problems.

Optimal power flow

Electricity flows through an AC network according to Kirchhoff's Laws. Transmission lines are subject to thermal limits (simple megawatt limits on flow), as well as voltage and electrical stability constraints.

The simulator must calculate the flows in the AC network that result from any given combination of unit commitment and generator megawatt dispatch, and ensure that AC line flows are within both the thermal limits and the voltage and stability constraints. This may include contingencies such as the loss of any one transmission or generation element - a so-called security-constrained optimal power flow (SCOPF), and if the unit commitment is optimized inside this framework we have a security-constrained unit commitment (SCUC).

In optimal power flow (OPF) the generalised scalar objective to be minimised is given by:

${\displaystyle f(u_0,x_0)}$

where u is a set of the control variables, x is a set of independent variables, and the subscript 0 indicates that the variable refers to the pre-contingency power system.

The SCOPF is bound by equality and inequality constraint limits. The equality constraint limits are given by the pre and post contingency power-flow equations, where k refers to the kth contingency case:

${\displaystyle g^k(u^k,x^k)=0\text{for }k=1,2,\dots ,n}$

The equipment and operating limits are given by the following inequalities:

${\displaystyle U_{min}^k\le U^k\le U_{max}^k}$ represent hard constraints on controls

${\displaystyle h_{min}^k\le X^k\le X_{max}^k}$ represents hard/soft constraints on variables

${\displaystyle h^k(u^k,x^k)\le 0\text{ for }k=0,1,\dots ,n}$ represents other constraints such as reactive reserve limits

The objective function in OPF can take on different forms relating to active or reactive power quantities that we wish to either minimise or maximise. For example we may wish to minimise transmission losses or minimise real power generation costs on a power network.

Other power flow solution methods like stochastic optimization incorporate the uncertainty found in modeling power systems by using the probability distributions of certain variables whose exact values are not known. When uncertainties in the constraints are present, such as for dynamic line ratings, chance constrained optimization can be used where the probability of violating a constraint is limited to a certain value. Another technique to model variability is the Monte Carlo method, in which different combinations of inputs and resulting outputs are considered based on the probability of their occurrence in the real world. This method can be applied to simulations for system security and unit commitment risk, and it is increasingly being used to model probabilistic load flow with renewable and/or distributed generation.

Models of competitive behavior

The cost of producing a megawatt of electrical energy is a function of:

1. fuel price
2. generation efficiency (the rate at which potential energy in the fuel is converted to electrical energy)
3. operations and maintenance costs

In addition to this, generating plant incur fixed costs including:

1. plant construction costs, and
2. fixed operations and maintenance costs

Assuming perfect competition, the market-based price of electricity would be based purely on the cost of producing the next megawatt of power, the so-called short-run marginal cost (SRMC). This price however might not be sufficient to cover the fixed costs of generation, and thus power market prices rarely show purely SRMC pricing. In most established power markets, generators are free to offer their generation capacity at prices of their choosing. Competition and use of financial contracts keeps these prices close to SRMC, but inevitably offers price above SRMC do occur (for example during the California energy crisis of 2001).

In the context of power system simulation, a number of techniques have been applied to simulate imperfect competition in electrical power markets:

1. Cournot competition
2. Bertrand competition
3. Supply function equilibrium
4. Residual Supply Index analysis

Various heuristics have also been applied to this problem. The aim is to provide realistic forecasts of power market prices, given the forecast supply-demand situation.

Long-term optimization

Power system long-term optimization focuses on optimizing the multi-year expansion and retirement plan for generation, transmission, and distribution facilities. The optimization problem will typically consider the long term investment cash flow and a simplified version of OPF / UC (Unit commitment), to make sure the power system operates in a secure and economic way. This area can be categorized as:

1. Generation expansion optimization
2. Transmission expansion optimization
3. Generation-transmission expansion co-optimization
4. Distribution network optimization

Study specifications

A well-defined power systems study requirement is critical to the success of any project as it will reduce the challenge of selecting the qualified service provider and the right analysis software. The system study specification describes the project scope, analysis types, and the required deliverable. The study specification must be written to match the specific project and industry requirements and will vary based on the type of analysis.

Power system simulation software

General Electric's MAPS (Multi-Area Production Simulation) is a production simulation model used by various Regional Transmission Organizations and Independent System Operators in the United States to plan for the economic impact of proposed electric transmission and generation facilities in FERC-regulated electric wholesale markets. Portions of the model may also be used for the commitment and dispatch phase (updated on 5 minute intervals) in operation of wholesale electric markets for RTO and ISO regions. Hitachi Energy's PROMOD is a similar software package. These ISO and RTO regions also utilize a GE software package called MARS (Multi-Area Reliability Simulation) to ensure the power system meets reliability criteria (a loss of load expectation (LOLE) of no greater than 0.1 days per year). Further, a GE software package called PSLF (Positive Sequence Load Flow), Siemens software packages called PSSE (Power System Simulation for Engineering) as well as PSS SINCAL (Siemens Network Calculator), and Electrical Transient Analyzer Program (ETAP) by Operation Technology Inc. analyzes load flow on the power system for short-circuits and stability during preliminary planning studies by RTOs and ISOs.

Zero-emissions vehicle

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Zero-emissions_vehicle 

Critical Mass cylists, San Francisco, April 29, 2005, and Muni Metro electric tram on J Church line

The Nissan Leaf electric car is a zero emission vehicle (ZEV).

A so-called zero-emission vehicle, or ZEV, is a vehicle that does not emit exhaust gas or other pollutants from the onboard source of power but still emits pollutants during its construction phase, production of energy carrier etc. Therefore, the term "zero-emission" has been described as abusive or greenwashing.

The California definition also adds that this includes under any and all possible operational modes and conditions. This is because under cold-start conditions for example, internal combustion engines tend to produce the maximum amount of pollutants. In a number of countries and states, transport is cited as the main source of greenhouse gases (GHG) and other pollutants. The desire to reduce this is thus politically strong.

Terminology

Harmful pollutants to the health and the environment include particulates (soot), hydrocarbons, carbon monoxide, ozone, lead, and various oxides of nitrogen. Although not considered emission pollutants by the original California Air Resources Board (CARB) or U.S. Environmental Protection Agency (EPA) definitions, the most recent common use of the term also includes volatile organic compounds, several air toxics (most notably 1,3-Butadiene), and global pollutants such as carbon dioxide and other greenhouse gases.

Examples of zero-emission vehicle with different power sources can include muscle-powered vehicles such as bicycles, electric bicycles, and gravity racers.

Motor vehicles

Also other battery electric vehicles, which may shift emissions to the location where the electricity is generated (if the electricity comes from coal or natural gas power plants—as opposed to hydro-electric, wind power, solar power or nuclear power plants); and fuel cell vehicles powered by hydrogen, which may shift emissions to the location where the hydrogen is generated. It does not include hydrogen internal combustion engine vehicles because these do generate some emissions (although being near-emissionless). It also does not include vehicles running on 100% biofuel as these also emit exhaust gases, despite being carbon neutral overall.

Emissions from the manufacturing process are thus not included in this definition, and it has been argued that the emissions that are created during manufacture are currently of an order of magnitude that is comparable to the emissions that are created during a vehicle's operating lifetime.

However, these vehicles are in the early stages of their development; the manufacturing emissions may decrease by the development of technology, industry, shifting toward mass production and the ever-increasing use of renewable energy throughout the supply-chains.

History

The Indian REVA electric car is a zero emissions vehicle (ZEV).

The Honda FCX Clarity, launched in 2008, is a fuel cell hydrogen vehicle compliant with the ZEV standard and sold in Japan and in the U.S. (only in Los Angeles).

Well-to-wheel emissions

The term zero-emissions or ZEV, as originally coined by the California Air Resources Board (CARB), refers only to motor vehicle emissions from the onboard source of power. Therefore, CARB's definition is accounting only for pollutants emitted at the point of the vehicle operation, and the clean air benefits are usually local because depending on the source of the electricity used to recharge the batteries, air pollutant emissions are shifted to the location of the electricity generation plants. In a broader perspective, the electricity used to recharge the batteries must be generated from renewable or clean sources such as wind, solar, hydroelectric, or nuclear power for ZEVs to have almost none or zero well-to-wheel emissions. In other words, if ZEVs are recharged from electricity generated by fossil fuel plants, they cannot be considered as zero emissions.

However, the spread of electrical-powered vehicles can help the development of systems for charging the EV batteries from excess electricity which cannot be used otherwise. For instance, electricity demand is lowest at night and the excess generated electricity at this time can be used for recharging the EVs' batteries. It's worth mentioning that renewable sources such as wind turbines or solar panels are less controllable in terms of the amount of generated electricity compared to fossil fuel power plants; most renewable energy sources are intermittent energy sources. Therefore, development of these resources will lead to excess energy which can be better used by development of EVs. Moreover, most EVs can benefit from regenerative brakes and other optimization systems which increases the energy efficiency in these vehicles.

Fuel cell vehicles (FCVs) can help even more in terms of the development of sustainable energy sources because these cars use hydrogen as their fuel. Compressed hydrogen can be used as an energy storage element, while electricity must be stored in batteries. The hydrogen can be produced by electricity through electrolysis, and this electricity can come from green sources. Hydrogen can be produced in situ, e.g. excess at wind farm when the generated electricity is not needed, or it can be connected to the grid to use the excess electricity from the grid and produce electricity, e.g. at hydrogen pump stations. As a result, development of FCVs can be a big step toward sustainable development and reducing GHG emission in a long-term perspective.

Other countries have a different definition of ZEV, noteworthy the more recent inclusion of greenhouse gases, as many European rules now regulate CO₂ emissions. CARB's role in regulating greenhouse gases began in 2004 based on the 2002 Pavley Act (AB 1493), but was blocked by lawsuits and by the EPA in 2007, by rejecting the required waiver. Additional responsibilities were granted to CARB by California's Global Warming Solutions Act of 2006 (AB 32), which includes the mandate to set low-carbon fuel standards.

As a result of an investigation into false advertising regarding "zero-emissions" claims, the Advertising Standards Authority (ASA) in the UK ruled in March 2010 to ban an advertisement from Renault UK regarding its "zero-emission vehicles" because the ad breached CAP (Broadcast) TV Code rules 5.1.1, 5.1.2 (Misleading advertising) and 5.2.1 (Misleading advertising- Evidence) and 5.2.6 (Misleading advertising-Environmental claims.)

Greenhouse gasses and other pollutant emissions are generated by vehicle manufacturing processes. The emissions from manufacturing are many factors larger than the emissions from tailpipes, even in gasoline engine vehicles. Most reports on ZEVs' impact to the climate do not take into account these manufacturing emissions, though over the lifetime of the car the emissions from manufacturing are relatively small.

Considering the current U.S. energy mix, a ZEV would produce an average 58% reduction in carbon dioxide emissions per mile driven. Given the current energy mixes in other countries, it has been predicted that such emissions would decrease by 40% in the U.K. and 19% in China.

Types of zero-emission vehicles

Further information: Railway electrification system

The Tesla Model S electric car is a zero-emission vehicle (ZEV) declared 2013 World Green Car of the Year.

Apart from animal-powered and human-powered vehicles, battery electric vehicles (which include cars, aircraft and boats) also do not emit any of the above pollutants, nor any CO₂ gases during use. This is a particularly important quality in densely populated areas, where the health of residents can be severely affected. However, the production of the fuels that power ZEVs, such as the production of hydrogen from fossil fuels, may produce more emissions per mile than the emissions produced from a conventional fossil fueled vehicle. A well-to-wheel life cycle assessment is necessary to understand the emissions implications associated with operating a ZEV.

Bicycles

Main articles: Bicycle and Electric bicycles

 

In the mid-19th century, bicycle ownership became common (during the bike boom)—predating mass car ownership. In the 1960s, the Flying Pigeon bicycle became the single most popular mechanized vehicle on the planet. Some 210 million electric bikes are on the road in China.

Motor vehicles

Segway Personal Transporters are two-wheeled, self-balancing, battery-powered machines that are eleven times more energy-efficient than the average American car. Operating on two lithium-ion batteries, the Segway PT produces zero emissions during operation, and utilizes a negligible amount of electricity while charging via a standard wall outlet.

Marine

See also: Electric boat and Sailboat

PlanetSolar

Wind-powered land vehicles operating on wind exist (using wind turbines and kites). For boats and other watercraft, regular and special sails (as rotorsails, wing sails, turbo sails, skysails) exist that can propel them without emissions.

Lloyd's Register has partnered with a consortium of companies to develop an ammonia-fuelled ship.

Air

Solar Impulse 2

Main article: Electric aircraft

An electric aircraft is an aircraft powered by electric motors. Electricity may be supplied by a variety of methods including batteries, ground power cables, solar cells, ultracapacitors, fuel cells and power beaming. Between 2015 and 2016, Solar Impulse 2 completed a circumnavigation of the Earth using solar power.

Incentives

See also: Subsidies and tax incentives by country

Subsidies for public transport

Japanese public transport is being driven in the direction of zero emissions due to growing environmental concern. Honda has launched a conceptual bus which features exercise machines to the rear of the vehicle to generate kinetic energy used for propulsion.

Due to the stop-start nature of idling in public transport, regenerative braking may be a possibility for public transport systems of the future.

Subsidies for development of electric cars

In an attempt to curb carbon emissions as well as noise pollution in South African cities, the South African Department of Science & Technology (DST), as well as other private investments, have made US$5 million available through the Innovation Fund for the development of the Joule. The Joule is a five-seater car, planned to be released in 2014. However the company ceased trading in 2012.

Low and zero emission zones

Several cities have implemented low-emission zones. Launched in 2019 and set to expand in 2023, the implementation of London's Ultra Low Emission Zone (ULEZ) incentivizes and accelerates the widespread adoption of cleaner vehicles through setting daily charge rates for driving vehicles that are non-compliant with ULEZ emission standards.