After compensating for varying signal delays resulting from the changing distance between an observer and a moving clock (i.e. Doppler effect), the observer will measure the moving clock as ticking more slowly than a clock at rest in the observer's own reference frame. In addition, a clock that is close to a massive body (and which therefore is at lower gravitational potential) will record less elapsed time than a clock situated farther from the same massive body (and which is at a higher gravitational potential).
These predictions of the theory of relativity have been repeatedly confirmed by experiment, and they are of practical concern, for instance in the operation of satellite navigation systems such as GPS and Galileo.
History
Time dilation by the Lorentz factor was predicted by several authors at the turn of the 20th century. Joseph Larmor (1897) wrote that, at least for those orbiting a nucleus, individual electrons describe corresponding parts of their orbits in times shorter for the [rest] system in the ratio: . Emil Cohn (1904) specifically related this formula to the rate of clocks. In the context of special relativity it was shown by Albert Einstein (1905) that this effect concerns the nature of time itself, and he was also the first to point out its reciprocity or symmetry. Subsequently, Hermann Minkowski (1907) introduced the concept of proper time which further clarified the meaning of time dilation.
Time dilation caused by a relative velocity
Special relativity indicates that, for an observer in an inertial frame of reference, a clock that is moving relative to the observer will be measured to tick slower than a clock at rest in the observer's frame of reference. This is sometimes called special relativistic time dilation. The faster the relative velocity, the greater the time dilation between them, with time slowing to a stop as one clock approaches the speed of light (299,792,458 m/s).
In theory, time dilation would make it possible for passengers in a fast-moving vehicle to advance into the future in a short period of their own time. With sufficiently high speeds, the effect would be dramatic. For example, one year of travel might correspond to ten years on Earth. Indeed, a constant 1 g acceleration would permit humans to travel through the entire known Universe in one human lifetime.
With current technology severely limiting the velocity of space travel, the differences experienced in practice are minuscule. After 6 months on the International Space Station (ISS), orbiting Earth at a speed of about 7,700 m/s, an astronaut would have aged about 0.005 seconds less than he would have on Earth. The cosmonauts Sergei Krikalev and Sergei Avdeyev both experienced time dilation of about 20 milliseconds compared to time that passed on Earth.
Simple inference
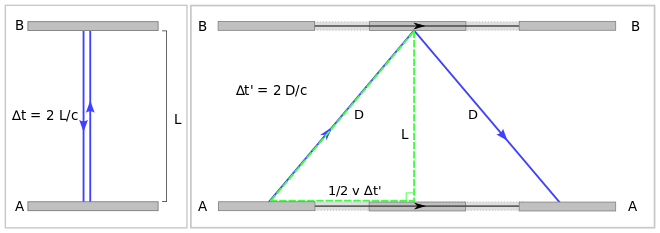
Right: Events according to an observer moving to the left of the setup: bottom mirror A when signal is generated at time t'=0, top mirror B when signal gets reflected at time t'=D/c, bottom mirror A when signal returns at time t'=2D/c
Time dilation can be inferred from the observed constancy of the speed of light in all reference frames dictated by the second postulate of special relativity. This constancy of the speed of light means that, counter to intuition, the speeds of material objects and light are not additive. It is not possible to make the speed of light appear greater by moving towards or away from the light source.
Consider then, a simple vertical clock consisting of two mirrors A and B, between which a light pulse is bouncing. The separation of the mirrors is L and the clock ticks once each time the light pulse hits mirror A.
In the frame in which the clock is at rest (see left part of the diagram), the light pulse traces out a path of length 2L and the time period between the ticks of the clock is equal to 2L divided by the speed of light c:
From the frame of reference of a moving observer traveling at the speed v relative to the resting frame of the clock (right part of diagram), the light pulse is seen as tracing out a longer, angled path 2D. Keeping the speed of light constant for all inertial observers requires a lengthening (that is dilation) of the time period between the ticks of this clock from the moving observer's perspective. That is to say, as measured in a frame moving relative to the local clock, this clock will be running (that is ticking) more slowly, since tick rate equals one over the time period between ticks 1/.
Straightforward application of the Pythagorean theorem leads to the well-known prediction of special relativity:
The total time for the light pulse to trace its path is given by:
The length of the half path can be calculated as a function of known quantities as:
Elimination of the variables D and L from these three equations results in:
which expresses the fact that the moving observer's period of the clock is longer than the period in the frame of the clock itself. The Lorentz factor gamma (γ) is defined as
Because all clocks that have a common period in the resting frame should have a common period when observed from the moving frame, all other clocks—mechanical, electronic, optical (such as an identical horizontal version of the clock in the example)—should exhibit the same velocity-dependent time dilation.
Reciprocity

Given a certain frame of reference, and the "stationary" observer described earlier, if a second observer accompanied the "moving" clock, each of the observers would perceive the other's clock as ticking at a slower rate than their own local clock, due to them both perceiving the other to be the one that is in motion relative to their own stationary frame of reference.
Common sense would dictate that, if the passage of time has slowed for a moving object, said object would observe the external world's time to be correspondingly sped up. Counterintuitively, special relativity predicts the opposite. When two observers are in motion relative to each other, each will measure the other's clock slowing down, in concordance with them being in motion relative to the observer's frame of reference.

While this seems self-contradictory, a similar oddity occurs in everyday life. If two persons A and B observe each other from a distance, B will appear small to A, but at the same time, A will appear small to B. Being familiar with the effects of perspective, there is no contradiction or paradox in this situation.
The reciprocity of the phenomenon also leads to the so-called twin paradox where the aging of twins, one staying on Earth and the other embarking on space travel, is compared, and where the reciprocity suggests that both persons should have the same age when they reunite. On the contrary, at the end of the round-trip, the traveling twin will be younger than the sibling on Earth. The dilemma posed by the paradox can be explained by the fact that situation is not symmetric. The twin staying on Earth is in a single inertial frame, and the traveling twin is in two different inertial frames: one on the way out and another on the way back. See also Twin paradox#Role of acceleration.
Experimental testing
Moving particles
- A comparison of muon lifetimes at different speeds is possible. In the laboratory, slow muons are produced; and in the atmosphere, very fast-moving muons are introduced by cosmic rays. Taking the muon lifetime at rest as the laboratory value of 2.197 μs, the lifetime of a cosmic-ray-produced muon traveling at 98% of the speed of light is about five times longer, in agreement with observations. An example is Rossi and Hall (1941), who compared the population of cosmic-ray-produced muons at the top of a mountain to that observed at sea level.
- The lifetime of particles produced in particle accelerators are longer due to time dilation. In such experiments, the "clock" is the time taken by processes leading to muon decay, and these processes take place in the moving muon at its own "clock rate", which is much slower than the laboratory clock. This is routinely taken into account in particle physics, and many dedicated measurements have been performed. For instance, in the muon storage ring at CERN the lifetime of muons circulating with γ = 29.327 was found to be dilated to 64.378 μs, confirming time dilation to an accuracy of 0.9 ± 0.4 parts per thousand.
Doppler effect
- The stated purpose by Ives and Stilwell (1938, 1941) of these
experiments was to verify the time dilation effect, predicted by
Larmor–Lorentz ether theory, due to motion through the ether using
Einstein's suggestion that Doppler effect in canal rays would provide a suitable experiment. These experiments measured the Doppler shift of the radiation emitted from cathode rays,
when viewed from directly in front and from directly behind. The high
and low frequencies detected were not the classically predicted values:The high and low frequencies of the radiation from the moving sources were measured as:as deduced by Einstein (1905) from the Lorentz transformation, when the source is running slow by the Lorentz factor.
- Hasselkamp, Mondry, and Scharmann
(1979) measured the Doppler shift from a source moving at right angles
to the line of sight. The most general relationship between frequencies
of the radiation from the moving sources is given by:as deduced by Einstein (1905). For ϕ = 90° (cos ϕ = 0) this reduces to fdetected = frestγ. This lower frequency from the moving source can be attributed to the time dilation effect and is often called the transverse Doppler effect and was predicted by relativity.
- In 2010 time dilation was observed at speeds of less than 10 metres per second using optical atomic clocks connected by 75 metres of optical fiber.
Proper time and Minkowski diagram
In the Minkowski diagram from the first image on the right, clock C resting in inertial frame S′ meets clock A at d and clock B at f (both resting in S). All three clocks simultaneously start to tick in S. The worldline of A is the ct-axis, the worldline of B intersecting f is parallel to the ct-axis, and the worldline of C is the ct′-axis. All events simultaneous with d in S are on the x-axis, in S′ on the x′-axis.
The proper time between two events is indicated by a clock present at both events. It is invariant, i.e., in all inertial frames it is agreed that this time is indicated by that clock. Interval df is, therefore, the proper time of clock C, and is shorter with respect to the coordinate times ef=dg of clocks B and A in S. Conversely, also proper time ef of B is shorter with respect to time if in S′, because event e was measured in S′ already at time i due to relativity of simultaneity, long before C started to tick.
From that it can be seen, that the proper time between two events indicated by an unaccelerated clock present at both events, compared with the synchronized coordinate time measured in all other inertial frames, is always the minimal time interval between those events. However, the interval between two events can also correspond to the proper time of accelerated clocks present at both events. Under all possible proper times between two events, the proper time of the unaccelerated clock is maximal, which is the solution to the twin paradox.
Derivation and formulation
In addition to the light clock used above, the formula for time dilation can be more generally derived from the temporal part of the Lorentz transformation. Let there be two events at which the moving clock indicates and , thus:
Since the clock remains at rest in its inertial frame, it follows , thus the interval is given by:
where Δt is the time interval between two co-local events (i.e. happening at the same place) for an observer in some inertial frame (e.g. ticks on their clock), known as the proper time, Δt′ is the time interval between those same events, as measured by another observer, inertially moving with velocity v with respect to the former observer, v is the relative velocity between the observer and the moving clock, c is the speed of light, and the Lorentz factor (conventionally denoted by the Greek letter gamma or γ) is:
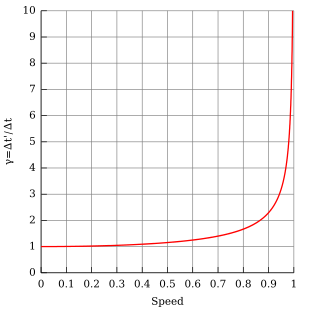
Thus the duration of the clock cycle of a moving clock is found to be increased: it is measured to be "running slow". The range of such variances in ordinary life, where v ≪ c, even considering space travel, are not great enough to produce easily detectable time dilation effects and such vanishingly small effects can be safely ignored for most purposes. As an approximate threshold, time dilation may become important when an object approaches speeds on the order of 30,000 km/s (1/10 the speed of light).
Hyperbolic motion
In special relativity, time dilation is most simply described in circumstances where relative velocity is unchanging. Nevertheless, the Lorentz equations allow one to calculate proper time and movement in space for the simple case of a spaceship which is applied with a force per unit mass, relative to some reference object in uniform (i.e. constant velocity) motion, equal to g throughout the period of measurement.
Let t be the time in an inertial frame subsequently called the rest frame. Let x be a spatial coordinate, and let the direction of the constant acceleration as well as the spaceship's velocity (relative to the rest frame) be parallel to the x-axis. Assuming the spaceship's position at time t = 0 being x = 0 and the velocity being v0 and defining the following abbreviation:
the following formulas hold:
Position:
Velocity:
Proper time as function of coordinate time:
In the case where v(0) = v0 = 0 and τ(0) = τ0 = 0 the integral can be expressed as a logarithmic function or, equivalently, as an inverse hyperbolic function:
As functions of the proper time of the ship, the following formulae hold:
Position:
Velocity:
Coordinate time as function of proper time:
Clock hypothesis
The clock hypothesis is the assumption that the rate at which a clock is affected by time dilation does not depend on its acceleration but only on its instantaneous velocity. This is equivalent to stating that a clock moving along a path measures the proper time, defined by:
The clock hypothesis was implicitly (but not explicitly) included in Einstein's original 1905 formulation of special relativity. Since then, it has become a standard assumption and is usually included in the axioms of special relativity, especially in light of experimental verification up to very high accelerations in particle accelerators.
Time dilation caused by gravity or acceleration


Gravitational time dilation is experienced by an observer that, at a certain altitude within a gravitational potential well, finds that their local clocks measure less elapsed time than identical clocks situated at higher altitude (and which are therefore at higher gravitational potential).
Gravitational time dilation is at play e.g. for ISS astronauts. While the astronauts' relative velocity slows down their time, the reduced gravitational influence at their location speeds it up, although to a lesser degree. Also, a climber's time is theoretically passing slightly faster at the top of a mountain compared to people at sea level. It has also been calculated that due to time dilation, the core of the Earth is 2.5 years younger than the crust. "A clock used to time a full rotation of the Earth will measure the day to be approximately an extra 10 ns/day longer for every km of altitude above the reference geoid." Travel to regions of space where extreme gravitational time dilation is taking place, such as near (but not beyond the event horizon of) a black hole, could yield time-shifting results analogous to those of near-lightspeed space travel.
Contrarily to velocity time dilation, in which both observers measure the other as aging slower (a reciprocal effect), gravitational time dilation is not reciprocal. This means that with gravitational time dilation both observers agree that the clock nearer the center of the gravitational field is slower in rate, and they agree on the ratio of the difference.
Experimental testing
- In 1959, Robert Pound and Glen A. Rebka measured the very slight gravitational redshift in the frequency of light emitted at a lower height, where Earth's gravitational field is relatively more intense. The results were within 10% of the predictions of general relativity. In 1964, Pound and J. L. Snider measured a result within 1% of the value predicted by gravitational time dilation. (See Pound–Rebka experiment)
- In 2010, gravitational time dilation was measured at the Earth's surface with a height difference of only one meter, using optical atomic clocks.
Combined effect of velocity and gravitational time dilation

High-accuracy timekeeping, low-Earth-orbit satellite tracking, and pulsar timing are applications that require the consideration of the combined effects of mass and motion in producing time dilation. Practical examples include the International Atomic Time standard and its relationship with the Barycentric Coordinate Time standard used for interplanetary objects.
Relativistic time dilation effects for the solar system and the Earth can be modeled very precisely by the Schwarzschild solution to the Einstein field equations. In the Schwarzschild metric, the interval is given by:
where:
- is a small increment of proper time (an interval that could be recorded on an atomic clock),
- is a small increment in the coordinate (coordinate time),
- are small increments in the three coordinates of the clock's position,
- represents the sum of the Newtonian gravitational potentials due to the masses in the neighborhood, based on their distances from the clock. This sum includes any tidal potentials.
The coordinate velocity of the clock is given by:
The coordinate time is the time that would be read on a hypothetical "coordinate clock" situated infinitely far from all gravitational masses (), and stationary in the system of coordinates (). The exact relation between the rate of proper time and the rate of coordinate time for a clock with a radial component of velocity is:
where:
- is the radial velocity,
- is the escape speed,
- , and are velocities as a percentage of speed of light c,
- is the Newtonian potential; hence equals half the square of the escape speed.
The above equation is exact under the assumptions of the Schwarzschild solution. It reduces to velocity time dilation equation in the presence of motion and absence of gravity, i.e. . It reduces to gravitational time dilation equation in the absence of motion and presence of gravity, i.e. .
Experimental testing

- Hafele and Keating, in 1971, flew caesium atomic clocks east and west around the Earth in commercial airliners, to compare the elapsed time against that of a clock that remained at the U.S. Naval Observatory. Two opposite effects came into play. The clocks were expected to age more quickly (show a larger elapsed time) than the reference clock since they were in a higher (weaker) gravitational potential for most of the trip (c.f. Pound–Rebka experiment). But also, contrastingly, the moving clocks were expected to age more slowly because of the speed of their travel. From the actual flight paths of each trip, the theory predicted that the flying clocks, compared with reference clocks at the U.S. Naval Observatory, should have lost 40±23 nanoseconds during the eastward trip and should have gained 275±21 nanoseconds during the westward trip. Relative to the atomic time scale of the U.S. Naval Observatory, the flying clocks lost 59±10 nanoseconds during the eastward trip and gained 273±7 nanoseconds during the westward trip (where the error bars represent standard deviation). In 2005, the National Physical Laboratory in the United Kingdom reported their limited replication of this experiment. The NPL experiment differed from the original in that the caesium clocks were sent on a shorter trip (London–Washington, D.C. return), but the clocks were more accurate. The reported results are within 4% of the predictions of relativity, within the uncertainty of the measurements.
- The Global Positioning System can be considered a continuously operating experiment in both special and general relativity. The in-orbit clocks are corrected for both special and general relativistic time dilation effects as described above, so that (as observed from the Earth's surface) they run at the same rate as clocks on the surface of the Earth.
In popular culture
Velocity and gravitational time dilation have been the subject of science fiction works in a variety of media. Some examples in film are the movies Interstellar and Planet of the Apes. In Interstellar, a key plot point involves a planet, which is close to a rotating black hole and on the surface of which one hour is equivalent to seven years on Earth due to time dilation. Physicist Kip Thorne collaborated in making the film and explained its scientific concepts in the book The Science of Interstellar.
Time dilation was used in the Doctor Who episodes "World Enough and Time" and "The Doctor Falls", which take place on a spaceship in the vicinity of a black hole. Due to the immense gravitational pull of the black hole and the ship's length (400 miles), time moves faster at one end than the other. When The Doctor's companion, Bill, gets taken away to the other end of the ship, she waits years for him to rescue her; in his time, only minutes pass. Furthermore, the dilation allows the Cybermen to evolve at a "faster" rate than previously seen in the show.
Tau Zero, a novel by Poul Anderson, is an early example of the concept in science fiction literature. In the novel, a spacecraft uses a Bussard ramjet to accelerate to high enough speeds that the crew spends five years on board, but thirty-three years pass on the Earth before they arrive at their destination. The velocity time dilation is explained by Anderson in terms of the tau factor which decreases closer and closer to zero as the ship approaches the speed of light—hence the title of the novel. Due to an accident, the crew is unable to stop accelerating the spacecraft, causing such extreme time dilation that the crew experiences the Big Crunch at the end of the universe. Other examples in literature, such as Rocannon's World, Hyperion and The Forever War, similarly make use of relativistic time dilation as a scientifically plausible literary device to have certain characters age slower than the rest of the universe.