Search This Blog

Saturday, October 31, 2015

Volcanic Caldera


From Wikipedia, the free encyclopedia


Example of the formation of a caldera, the pictures show Mount Mazama's eruption timeline

A caldera is a cauldron-like volcanic feature on large central volcanoes, a special sort of volcanic crater (from one to several kilometers in diameter), formed when a magma chamber was emptied. The depression then originated either in very big explosive eruptions or in erosion and collapse of the magma chamber roof. The previous emptying of this magma chamber is often accomplished during a series of effusive eruptions in the volcanic system, even kilometers away from the magma chamber itself.

Etymology

The word comes from Spanish caldera, and this from Latin caldaria, meaning "cooking pot". In some texts the English term cauldron is also used.The term caldera was introduced into the geological vocabulary by the German geologist Leopold von Buch when he published his memoirs of his 1815 visit to the Canary Islands,[note 1] where he first saw the Las Cañadas caldera on Tenerife, with Montaña Teide dominating the landscape, and then the Caldera de Taburiente on La Palma.

Caldera formation


Animation of analogue experiment showing origin of volcanic caldera in box filled with flour.

Landsat image of Lake Toba, on the island of Sumatra, Indonesia. A resurgent dome formed the island of Samosir. (100 km/62 mi long and 30 km/19 mi wide, a caldera of the world's largest class)

A collapse is triggered by the emptying of the magma chamber beneath the volcano, sometimes as the result of a large explosive volcanic eruption (see Tambora in 1815), but also during effusive eruptions on the flanks of a volcano (see Piton de la Fournaise in 2007) or in a connected fissure system (see Bárðarbunga in 2014/15). If enough magma is ejected, the emptied chamber is unable to support the weight of the volcanic edifice above it. A roughly circular fracture, the "ring fault", develops around the edge of the chamber. Ring fractures serve as feeders for fault intrusions which are also known as ring dykes. Secondary volcanic vents may form above the ring fracture. As the magma chamber empties, the center of the volcano within the ring fracture begins to collapse. The collapse may occur as the result of a single cataclysmic eruption, or it may occur in stages as the result of a series of eruptions. The total area that collapses may be hundreds or thousands of square kilometers.

Mineralization

Some calderas are known to host rich ore deposits. One of the world's best-preserved mineralized calderas is the Sturgeon Lake Caldera in northeastern Ontario, Canada, which formed during the Neoarchean era[1] about 2,700 million years ago.[2]

Explosive caldera eruptions

If the magma is rich in silica, the caldera is often filled in with ignimbrite, tuff, rhyolite, and other igneous rocks. Silica-rich magma has a high viscosity, and therefore does not flow easily like basalt. 
As a result, gases tend to become trapped at high pressure within the magma. When the magma approaches the surface of the Earth, the rapid off-loading of overlying material causes the trapped gases to decompress rapidly, thus triggering explosive destruction of the magma and spreading volcanic ash over wide areas. Further lava flows may be erupted.
If volcanic activity continues, the center of the caldera may be uplifted in the form of a resurgent dome such as is seen at Cerro Galán, Lake Toba, Yellowstone, etc., by subsequent intrusion of magma. A silicic or rhyolitic caldera may erupt hundreds or even thousands of cubic kilometers of material in a single event. Even small caldera-forming eruptions, such as Krakatoa in 1883 or Mount Pinatubo in 1991, may result in significant local destruction and a noticeable drop in temperature around the world. Large calderas may have even greater effects.

When Yellowstone Caldera last erupted some 650,000 years ago, it released about 1,000 km3 of material (as measured in dense rock equivalent (DRE)), covering a substantial part of North America in up to two metres of debris. By comparison, when Mount St. Helens erupted in 1980, it released ~1.2 km3 (DRE) of ejecta. The ecological effects of the eruption of a large caldera can be seen in the record of the Lake Toba eruption in Indonesia.

Toba

About 74,000 years ago, this Indonesian volcano released about 2,800 km3 DRE of ejecta, the largest known eruption within the Quaternary Period (last 1.8 million years) and the largest known explosive eruption within the last 25 million years. In the late 1990s, anthropologist Stanley Ambrose[3] proposed that a volcanic winter induced by this eruption reduced the human population to about 2,000 - 20,000 individuals, resulting in a population bottleneck (see Toba catastrophe theory). More recently several geneticists, including Lynn Jorde and Henry Harpending have proposed that the human race was reduced to approximately five to ten thousand people.[4] However, there is no direct evidence that the theory is correct. And there is no evidence for any other animal decline or extinction, even in environmentally sensitive species.[5] There is evidence that human habitation continued in India after the eruption.[6] The theory in its strongest form may be incorrect.

Eruptions forming even larger calderas are known, especially La Garita Caldera in the San Juan Mountains of Colorado, where the 5,000-km3 Fish Canyon Tuff was blasted out in a single major eruption about 27.8 million years ago.

At some points in geological time, rhyolitic calderas have appeared in distinct clusters. The remnants of such clusters may be found in places such as the San Juan Mountains of Colorado (formed during the Oligocene, Miocene, and Pliocene periods) or the Saint Francois Mountain Range of Missouri (erupted during the Proterozoic).


Satellite photograph of the summit caldera on Fernandina Island in the Galapagos archipelago.

Oblique aerial photo of Nemrut Caldera, Van Lake, Eastern Turkey

Non-explosive calderas


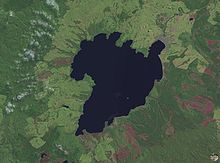
Sollipulli Caldera, located in central Chile near the border with Argentina, filled with ice. The volcano sits in the southern Andes Mountains within Chile’s Parque Nacional Villarica.[7]

Some volcanoes, such as shield volcanoes Kīlauea and Mauna Loa (respectively the most active and second largest on Earth, are both on the island of Hawaii), form calderas in a different fashion. The magma feeding these volcanoes is basalt which is silica poor. As a result, the magma is much less viscous than the magma of a rhyolitic volcano, and the magma chamber is drained by large lava flows rather than by explosive events. The resulting calderas are also known as subsidence calderas, and can form more gradually than explosive calderas. For instance, the caldera atop Fernandina Island underwent a collapse in 1968, when parts of the caldera floor dropped 350 meters.[8] Kilauea Caldera has an inner crater known as Halema‘uma‘u, which has often been filled by a lava lake.

In April 2007, during the eruption, the summit floor of the Piton de la Fournaise on the island of Réunion the floor of the main crater suddenly dropped about 300 m. This was attributed to the withdrawal of magma which was being erupted through a vent lower down on the southern flank of the volcano.

Another process that may allow a caldera to form can occur if molten lava can escape through a breach on the caldera's rim.

Extraterrestrial calderas

Since the early 1960s, it has been known that volcanism has occurred on other planets and moons in the Solar System. Through the use of manned and unmanned spacecraft, volcanism has been discovered on Venus, Mars, the Moon, and Io, a satellite of Jupiter. None of these worlds have plate tectonics, which contributes approximately 60% of the Earth's volcanic activity (the other 40% is attributed to hotspot volcanism).[9] Caldera structure is similar on all of these planetary bodies, though the size varies considerably. The average caldera diameter on Venus is 68 km. The average caldera diameter on Io is close to 40 km, and the mode is 6 km; Tvashtar Paterae is likely the largest caldera with a diameter of 290 km. The average caldera diameter on Mars is 48 km, smaller than Venus. Calderas on Earth are the smallest of all planetary bodies and vary from 1.6 to 80 km as a maximum.[10]

The Moon

The Moon has an outer shell of low-density crystalline rock that is a few hundred kilometers thick, which formed due to a rapid creation. The craters of the moon have been well preserved through time and were once thought to have been the result of extreme volcanic activity, but actually were formed by meteorites, nearly all of which took place in the first few hundred million years after the Moon formed. Around 500 million years afterward, the Moon's mantle was able to be extensively melted due to the decay of radioactive elements. Massive basaltic eruptions took place generally at the base of large impact craters. Also, eruptions may have taken place due to a magma reservoir at the base of the crust. This forms a dome, possibly the same morphology of a shield volcano where calderas universally are known to form.[9] Although caldera-like structures are rare on the Moon, they are not completely absent. The Compton-Belkovich Volcanic Complex on the far side of the Moon is thought to be a caldera, possibly an ash-flow caldera.[11]

Mars

The volcanic activity of Mars is concentrated in two major provinces: Tharsis and Elysium. Each province contains a series of giant shield volcanoes that are similar to what we see on Earth and likely are the result of mantle hot spots. The surfaces are dominated by lava flows, and all have one or more collapse calderas.[9] Mars has the largest volcano in the Solar System, Olympus Mons, which is more than three times the height of Mount Everest, with a diameter of 520 km (323 miles). The summit of the mountain has six nested calderas.[12]

Venus

Because there are no plate tectonics on Venus, heat is only lost by conduction through the lithosphere. This causes enormous lava flows, accounting for 80% of Venus' surface area. Many of the mountains are large shield volcanoes that range in size from 150–400 km in diameter and 2–4 km high. More than 80 of these large shield volcanoes have summit calderas averaging 60 km across.[9]

Io

Io, unusually, is heated by solid flexing due to the tidal influence of Jupiter and Io's orbital resonance with neighboring large moons Europa and Ganymede, which keeps its orbit slightly eccentric. Unlike any of the planets mentioned, Io is continuously volcanically active. For example, the NASA Voyager 1 and Voyager 2 spacecraft detected nine erupting volcanoes while passing Io in 1979. Io has many calderas with diameters tens of kilometers across.[9]

List of volcanic calderas

Erosion calderas


at

Friday, October 30, 2015

Solar irradiance


From Wikipedia, the free encyclopedia

Solar irradiance (also Insolation, from Latin insolare, to expose to the sun)[1][2] is the power per unit area produced by the Sun in the form of electromagnetic radiation. Irradiance may be measured in space or at the Earth's surface after atmospheric absorption and scattering. Total solar irradiance (TSI), is a measure of the solar radiative power per unit area normal to the rays, incident on the Earth's upper atmosphere. The solar constant is a conventional measure of mean TSI at a distance of one Astronomical Unit (AU). Irradiance is a function of distance from the Sun, the solar cycle, and cross-cycle changes.[3] Irradiance on Earth is most intense at points directly facing (normal to) the Sun.


Annual mean insolation at the top of Earth's atmosphere (TOA) and at the planet's surface

Units

The unit recommended by the World Meteorological Organization is the megajoule per square metre (MJ/m2) or joule per square millimetre (J/mm2).[4]

An alternate unit of measure is the Langley (1 thermochemical calorie per square centimeter or 41,840 J/m2) or irradiance per unit time.

The solar energy business uses watt-hour per square metre (Wh/m2). Divided by the recording time, this measure becomes insolation, another unit of irradiance.

Insolation can be measured in space, at the edge of the atmosphere or at a terrestrial object.
Insolation can also be expressed in Suns, where one Sun equals 1000 W/m2 at the point of arrival, with kWh/m2/day expressed as hours/day.[5]

Absorption and reflection[edit source | edit]

Solar irradiance spectrum above atmosphere and at surface

Reaching an object, part of the irradiance is absorbed and the remainder reflected. Usually the absorbed radiation is converted to thermal energy, increasing the object's temperature. Manmade or natural systems, however, can convert part of the absorbed radiation into another form such as electricity or chemical bonds, as in the case of photovoltaic cells or plants. The proportion of reflected radiation is the object's reflectivity or albedo.

Projection effect


One sunbeam one mile wide shines on the ground at a 90° angle, and another at a 30° angle. The oblique sunbeam distributes its light energy over twice as much area.

Insolation onto a surface is largest when the surface directly faces (is normal to) the sun. As the angle between the surface and the Sun moves from normal, the insolation is reduced in proportion to the angle's Cosine; see Effect of sun angle on climate.

In the figure, the angle shown is between the ground and the sunbeam rather than between the vertical direction and the sunbeam; hence the sine rather than the cosine is appropriate. A sunbeam one mile (1.6 km) wide arrives from directly overhead, and another at a 30° angle to the horizontal. The Sine of a 30° angle is 1/2, whereas the sine of a 90° angle is 1. Therefore, the angled sunbeam spreads the light over twice the area. Consequently, half as much light falls on each square mile.

This 'projection effect' is the main reason why Earth's polar regions are much colder than equatorial regions. On an annual average the poles receive less insolation than does the equator, because the poles are always angled more away from the sun than the tropics. At a lower angle the light must travel through more atmosphere. This attenuates it (by absorption and scattering) further reducing insolation.

Categories


Solar potential – global horizontal irradiation

Direct insolation is measured at a given location with a surface element perpendicular to the Sun. It excludes diffuse insolation (radiation that is scattered or reflected by atmospheric components). Direct insolation is equal to the Solar constant minus the atmospheric losses due to absorption and scattering. While the solar constant varies, losses depend on time of day (length of light's path through the atmosphere depending on the Solar elevation angle), Cloud cover, Moisture content and other contents. Insolation affects plant metabolism and animal behavior.[6]

Diffuse insolation is the contribution of light scattered by the atmosphere to total insolation.

Earth

Average annual solar radiation arriving at the top of the Earth's atmosphere is roughly 1366 W/m2.[7][8] The radiation is distributed across the Electromagnetic spectrum, although most is Visible light. The Sun's rays are attenuated as they pass through the Atmosphere, leaving maximum normal surface irradiance at approximately 1000 W /m2 at Sealevel on a clear day.[clarification needed]


A Pyranometer, a component of a temporary remote meteorological station, measures insolation on Skagit Bay, Washington.

The actual figure varies with the Sun's angle and atmospheric circumstances. Ignoring clouds, the daily average irradiance for the Earth is approximately 6 kWh/m2 = 21.6 MJ/m2. The output of, for example, a photovoltaic panel, partly depends on the angle of the sun relative to the panel. One Sun is a unit of power flux, not a standard value for actual insolation. Sometimes this unit is referred to as a Sol, not to be confused with a sol, meaning one solar day.[9]

Solar potential maps

  • North America
  • South America
  • Europe
  • Africa and Middle East
  • South and South-East Asia
  • Australia

Top of the atmosphere


Spherical triangle for application of the spherical law of cosines for the calculation the solar zenith angle Θ for observer at latitude φ and longitude λ from knowledge of the hour angle h and solar declination δ. (δ is latitude of subsolar point, and h is relative longitude of subsolar point).

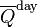\overline{Q}^{\mathrm{day}}, the theoretical daily-average insolation at the top of the atmosphere, where θ is the polar angle of the Earth's orbit, and θ = 0 at the vernal equinox, and θ = 90° at the summer solstice; φ is the latitude of the Earth. The calculation assumed conditions appropriate for 2000 A.D.: a solar constant of S0 = 1367 W m−2, obliquity of ε = 23.4398°, longitude of perihelion of ϖ = 282.895°, eccentricity e = 0.016704. Contour labels (green) are in units of W m−2.

The distribution of solar radiation at the top of the atmosphere is determined by Earth's sphericity and orbital parameters. This applies to any unidirectional beam incident to a rotating sphere. Insolation is essential for numerical weather prediction and understanding seasons and climate change. Application to ice ages is known as Milankovitch cycles.

Distribution is based on a fundamental identity from Spherical trigonometry, the spherical law of cosines:
\cos(c) = \cos(a) \cos(b) + \sin(a) \sin(b) \cos(C) \,
 
where a, b and c are arc lengths, in radians, of the sides of a spherical triangle. C is the angle in the vertex opposite the side which has arc length c. Applied to the calculation of Solar zenith angle Θ, the following applies to the Spherical law of cosines:
C=h \,
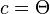
c=\Theta \,
a=\tfrac{1}{2}\pi-\phi \,
b=\tfrac{1}{2}\pi-\delta \,
\cos(\Theta) = \sin(\phi) \sin(\delta) + \cos(\phi) \cos(\delta) \cos(h) \,
The separation of Earth from the sun can be denoted RE and the mean distance can be denoted R0, approximately 1 AU. The solar constant is denoted S0. The solar flux density (insolation) onto a plane tangent to the sphere of the Earth, but above the bulk of the atmosphere (elevation 100 km or greater) is:
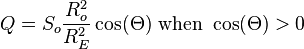
Q = S_o \frac{R_o^2}{R_E^2}\cos(\Theta)\text{ when }\cos(\Theta)>0
and
Q=0\text{ when }\cos(\Theta)\le 0 \,
The average of Q over a day is the average of Q over one rotation, or the hour angle progressing from h = π to h = −π:
\overline{Q}^{\text{day}} = -\frac{1}{2\pi}{\int_{\pi}^{-\pi}Q\,dh}
Let h0 be the hour angle when Q becomes positive. This could occur at sunrise when \Theta=\tfrac{1}{2}\pi, or for h0 as a solution of
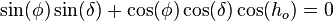
\sin(\phi) \sin(\delta) + \cos(\phi) \cos(\delta) \cos(h_o) = 0 \,
or
\cos(h_o)=-\tan(\phi)\tan(\delta)
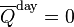If tan(φ)tan(δ) > 1, then the sun does not set and the sun is already risen at h = π, so ho = π. If tan(φ)tan(δ) < −1, the sun does not rise and \overline{Q}^{\mathrm{day}}=0.
\frac{R_o^2}{R_E^2}
is nearly constant over the course of a day, and can be taken outside the integral
\int_\pi^{-\pi}Q\,dh = \int_{h_o}^{-h_o}Q\,dh = S_o\frac{R_o^2}{R_E^2}\int_{h_o}^{-h_o}\cos(\Theta)\, dh
\int_\pi^{-\pi}Q\,dh = S_o\frac{R_o^2}{R_E^2}\left[ h \sin(\phi)\sin(\delta) + \cos(\phi)\cos(\delta)\sin(h) \right]_{h=h_o}^{h=-h_o}
\int_\pi^{-\pi}Q\,dh = -2 S_o\frac{R_o^2}{R_E^2}\left[ h_o \sin(\phi) \sin(\delta) + \cos(\phi) \cos(\delta) \sin(h_o) \right]
\overline{Q}^{\text{day}} = \frac{S_o}{\pi}\frac{R_o^2}{R_E^2}\left[ h_o \sin(\phi) \sin(\delta) + \cos(\phi) \cos(\delta) \sin(h_o) \right]
Let θ be the conventional polar angle describing a planetary orbit. Let θ = 0 at the vernal equinox. The declination δ as a function of orbital position is
\sin \delta = \sin \varepsilon~\sin(\theta - \varpi )\,
where ε is the obliquity. The conventional longitude of perihelion ϖ is defined relative to the vernal equinox, so for the elliptical orbit:
R_E=\frac{R_o}{1+e\cos(\theta-\varpi)}
or
\frac{R_o}{R_E}={1+e\cos(\theta-\varpi)}
With knowledge of ϖ, ε and e from astrodynamical calculations [10] and So from a consensus of observations or theory, \overline{Q}^{\mathrm{day}}can be calculated for any latitude φ and θ. Because of the elliptical orbit, and as a consequence of Kepler's second law, θ does not progress uniformly with time. Nevertheless, θ = 0° is exactly the time of the vernal equinox, θ = 90° is exactly the time of the summer solstice, θ = 180° is exactly the time of the autumnal equinox and θ = 270° is exactly the time of the winter solstice.

Variation

Total irradiance

Total solar irradiance (TSI)[11] changes slowly on decadal and longer timescales. The variation during solar cycle 21 was about 0.1% (peak-to-peak).[12] In contrast to older reconstructions,[13] most recent TSI reconstructions point to an increase of only about 0.05% to 0.1% between the Maunder Minimum and the present.[14][15][16]

Ultraviolet irradiance

Ultraviolet irradiance (EUV) varies by approximately 1.5 percent from solar maxima to minima, for 200 to 300 nm wavelengths.[17] However, a proxy study estimated that UV has increased by 3.0% since the Maunder Minimum.[18]

Milankovitch cycles

Milankovitch Variations.png

Some variations in insolation are not due to solar changes but rather due to the Earth moving between its perigee and apogee, or changes in the latitudinal distribution of radiation. These orbital changes or Milankovitch cycles have caused radiance variations of as much as 25% (locally; global average changes are much smaller) over long periods. The most recent significant event was an axial tilt of 24° during boreal summer near the Holocene climatic optimum.

Obtaining a time series for a \overline{Q}^{\mathrm{day}} for a particular time of year, and particular latitude, is a useful application in the theory of Milankovitch cycles. For example, at the summer solstice, the declination δ is equal to the obliquity ε. The distance from the sun is
\frac{R_o}{R_E} = 1+e\cos(\theta-\varpi) = 1+e\cos(\tfrac{\pi}{2}-\varpi) = 1 + e \sin(\varpi)
For this summer solstice calculation, the role of the elliptical orbit is entirely contained within the important product e \sin(\varpi), the precession index, whose variation dominates the variations in insolation at 65° N when eccentricity is large. For the next 100,000 years, with variations in eccentricity being relatively small, variations in obliquity dominate.

Measurement

The space-based TSI record comprises measurements from more than ten radiometers spanning three solar cycles.

Technique

All modern TSI satellite instruments employ active cavity electrical substitution radiometry. This technique applies measured electrical heating to maintain an absorptive blackened cavity in thermal equilibrium while incident sunlight passes through a precision aperture of calibrated area. The aperture is modulated via a shutter. Accuracy uncertainties of <0.01% are required to detect long term solar irradiance variations, because expected changes are in the range 0.05 to 0.15 W m−2 per century.[19]

Intertemporal calibration

In orbit, radiometric calibrations drift for reasons including solar degradation of the cavity, electronic degradation of the heater, surface degradation of the precision aperture and varying surface emissions and temperatures that alter thermal backgrounds. These calibrations require compensation to preserve consistent measurements.[19]

For various reasons, the sources do not always agree. The Solar Radiation and Climate Experiment/Total Irradiance Measurement (SORCE/TIM) TSI values are lower than prior measurements by the Earth Radiometer Budget Experiment (ERBE) on the Earth Radiation Budget Satellite (ERBS), VIRGO on the Solar Heliospheric Observatory (SoHO) and the ACRIM instruments on the Solar Maximum Mission (SMM), Upper Atmosphere Research Satellite (UARS) and ACRIMSat. Pre-launch ground calibrations relied on component rather than system level measurements, since irradiance standards lacked absolute accuracies.[19]

Measurement stability involves exposing different radiometer cavities to different accumulations of solar radiation to quantify exposure-dependent degradation effects. These effects are then compensated for in final data. Observation overlaps permits corrections for both absolute offsets and validation of instrumental drifts.[19]

Uncertainties of individual observations exceed irradiance variability (∼0.1%). Thus, instrument stability and measurement continuity are relied upon to compute real variations.

Long-term radiometer drifts can be mistaken for irradiance variations that can be misinterpreted as affecting climate. Examples include the issue of the irradiance increase between cycle minima in 1986 and 1996, evident only in the ACRIM composite (and not the model) and the low irradiance levels in the PMOD composite during the 2008 minimum.

Despite the fact that ACRIM I, ACRIM II, ACRIM III, VIRGO and TIM all track degradation with redundant cavities, notable and unexplained differences remain in irradiance and the modeled influences of sunspots and faculae.

Persistent inconsistencies

Disagreement among overlapping observations indicates unresolved drifts that suggest the TSI record is not sufficiently stable to discern solar changes on decadal time scales. Only the ACRIM composite shows irradiance increasing by ∼1 W m−2 between 1986 and 1996; this change is also absent in the model.[19]

Recommendations to resolve the instrument discrepancies include validating optical measurement accuracy by comparing ground-based instruments to laboratory references, such as those at National Institute of Science and Technology (NIST); NIST validation of aperture area calibrations uses spares from each instrument; and applying diffraction corrections from the view-limiting aperture.[19]

For ACRIM, NIST determined that diffraction from the view-limiting aperture contributes a 0.13% signal not accounted for in the three ACRIM instruments. This correction lowers the reported ACRIM values, bringing ACRIM closer to TIM. In ACRIM and all other instruments, the aperture is deep inside the instrument, with a larger view-limiting aperture at the front. Depending on edge imperfections this can directly scatter light into the cavity. This design admits two to three times the amount of light intended to be measured; if not completely absorbed or scattered, this additional light produces erroneously high signals. In contrast, TIM's design places the precision aperture at the front so that only desired light enters.[19]

Variations from other sources likely include an annual cycle that is nearly in phase with the Sun-Earth distance in ACRIM III data and 90-day spikes in the VIRGO data coincident with SoHO spacecraft maneuvers that were most apparent during the 2008 solar minimum.

TSI Radiometer Facility

TIM's high absolute accuracy creates new opportunities for measuring climate variables. TSI Radiometer Facility (TRF) is a cryogenic radiometer that operates in a vacuum with controlled light sources. L-1 Standards and Technology (LASP) designed and built the system, completed in 2008. It was calibrated for optical power against the NIST Primary Optical Watt Radiometer, a cryogenic radiometer that maintains the NIST radiant power scale to an uncertainty of 0.02% (1σ). As of 2011 TRF was the only facility that approached the desired <0.01% uncertainty for pre-launch validation of solar radiometers measuring irradiance (rather than merely optical power) at solar power levels and under vacuum conditions.[19]

TRF encloses both the reference radiometer and the instrument under test in a common vacuum system that contains a stationary, spatially uniform illuminating beam. A precision aperture with area calibrated to 0.0031% (1σ) determines the beam's measured portion. The test instrument's precision aperture is positioned in the same location, without optically altering the beam, for direct comparison to the reference. Variable beam power provides linearity diagnostics, and variable beam diameter diagnoses scattering from different instrument components.[19]

The Glory/TIM and PICARD/PREMOS flight instrument absolute scales are now traceable to the TRF in both optical power and irradiance. The resulting high accuracy reduces the consequences of any future gap in the solar irradiance record.[19]

Difference Relative to TRF[19]
Instrument Irradiance: View-Limiting Aperture Overfilled Irradiance: Precision Aperture Overfilled Difference Attributable To Scatter Error Measured Optical Power Error Residual Irradiance Agreement Uncertainty
SORCE/TIM ground NA −0.037% NA −0.037% 0.000% 0.032%
Glory/TIM flight NA −0.012% NA −0.029% 0.017% 0.020%
PREMOS-1 ground −0.005% −0.104% 0.098% −0.049% −0.104% ∼0.038%
PREMOS-3 flight 0.642% 0.605% 0.037% 0.631% −0.026% ∼0.027%
VIRGO-2 ground 0.897% 0.743% 0.154% 0.730% 0.013% ∼0.025%

2011 reassessment

The most probable value of TSI representative of solar minimum is 1360.8 ± 0.5 W m−2, lower than the earlier accepted value of 1365.4 ± 1.3 W m−2, established in the 1990s. The new value came from SORCE/TIM and radiometric laboratory tests. Scattered light is a primary cause of the higher irradiance values measured by earlier satellites in which the precision aperture is located behind a larger, view-limiting aperture. The TIM uses a view-limiting aperture that is smaller than precision aperture that precludes this spurious signal. The new estimate is from better measurement rather than a change in solar output.[19]

A regression model-based split of the relative proportion of sunspot and facular influences from SORCE/TIM data accounts for 92% of observed variance and tracks the observed trends to within TIM's stability band. This agreement provides further evidence that TSI variations are primarily due to solar surface magnetic activity.[19]

Instrument inaccuracies add a significant uncertainty in determining Earth's energy balance. The energy imbalance has been variously measured (during a deep solar minimum of 2005–2010) to be +0.58 ± 0.15 W/m²),[20] +0.60 ± 0.17 W/m²[21] and +0.85 W m−2. Estimates from space-based measurements range from +3 to 7 W m−2. SORCE/TIM's lower TSI value reduces this discrepancy by 1 W m−2. This difference between the new lower TIM value and earlier TSI measurements corresponds to a climate forcing of −0.8 W m−2, which is comparable to the energy imbalance.[19]

2014 reassessment

In 2014 a new ACRIM composite was developed using the updated ACRIM3 record. It added corrections for scattering and diffraction revealed during recent testing at TRF and two algorithm updates. The algorithm updates more accurately account for instrument thermal behavior and parsing of shutter cycle data. These corrected a component of the quasi-annual signal and increased the signal to noise ratio, respectively. The net effect of these corrections decreased the average ACRIM3 TSI value without affecting the trending in the ACRIM Composite TSI.[22]

Differences between ACRIM and PMOD TSI composites are evident, but the most significant is the solar minimum-to-minimum trends during solar cycles 21-23. ACRIM established an increase of +0.037%/decade from 1980 to 2000 and a decrease thereafter. PMOD instead presents a steady decrease since 1978. Significant differences can also be seen during the peak of solar cycles 21 and 22. These arise from the fact that ACRIM uses the original TSI results published by the satellite experiment teams while PMOD significantly modifies some results to conform them to specific TSI proxy models. The implications of increasing TSI during the global warming of the last two decades of the 20th century are that solar forcing may be a significantly larger factor in climate change than represented in the CMIP5 general circulation climate models.[22]

Applications

Buildings

In construction, insolation is an important consideration when designing a building for a particular site.[23]


Insolation variation by month; 1984–1993 averages for January (top) and April (bottom)

The projection effect can be used to design buildings that are cool in summer and warm in winter, by providing vertical windows on the equator-facing side of the building (the south face in the northern hemisphere, or the north face in the southern hemisphere): this maximizes insolation in the winter months when the Sun is low in the sky and minimizes it in the summer when the Sun is high. (The Sun's north/south path through the sky spans 47 degrees through the year).

Solar power

Insolation figures are used as an input to worksheets to size solar power systems.[24] Because (except for asphalt solar collectors)[25] panels are almost always mounted at an angle[26] towards the sun, insolation must be adjusted to prevent estimates that are inaccurately low for winter and inaccurately high for summer.[27] In many countries the figures can be obtained from an insolation map or from insolation tables that reflect data over the prior 30–50 years. Photovoltaic panels are rated under standard conditions to determine the Wp rating (watts peak),[28] which can then be used with insolation to determine the expected output, adjusted by factors such as tilt, tracking and shading (which can be included to create the installed Wp rating).[29] Insolation values range from 800 to 950 kWh/(kWp·y) in Norway to up to 2,900 in Australia.

Climate research

Irradiance plays a part in climate modeling and weather forecasting. A non-zero average global net radiation at the top of the atmosphere is indicative of Earth's thermal disequilibrium as imposed by climate forcing.

The impact of the lower 2014 TSI value on climate models is unknown. A few tenths of a percent change in the absolute TSI level is typically considered to be of minimal consequence for climate simulations. The new measurements require climate model parameter adjustments.

Experiments with GISS Model 3 investigated the sensitivity of model performance to the TSI absolute value during present and pre-industrial epochs, and describe, for example, how the irradiance reduction is partitioned between the atmosphere and surface and the effects on outgoing radiation.[19]

Assessing the impact of long-term irradiance changes on climate requires greater instrument stability[19] combined with reliable global surface temperature observations to quantify climate response processes to radiative forcing on decadal time scales. The observed 0.1% irradiance increase imparts 0.22 W m−2 climate forcing, which suggests a transient climate response of 0.6 °C per W m−2. This response is larger by a factor of 2 or more than in the IPCC-assessed 2008 models, possibly appearing in the models' heat uptake by the ocean.[19]

Space travel

Insolation is the primary variable affecting equilibrium temperature in spacecraft design and planetology.

Solar activity and irradiance measurement is a concern for space travel. For example, the American space agency, NASA, launched its Solar Radiation and Climate Experiment (SORCE) satellite with Solar Irradiance Monitors.[3]

Civil engineering

In civil engineering and hydrology, numerical models of snowmelt runoff use observations of insolation. This permits estimation of the rate at which water is released from a melting snowpack. Field measurement is accomplished using a pyranometer.

Conversion factor (multiply top row by factor to obtain side column)
W/m2 kW·h/(m2·day) sun hours/day kWh/(m2·y) kWh/(kWp·y)
W/m2 1 41.66666 41.66666 0.1140796 0.1521061
kW·h/(m2·day) 0.024 1 1 0.0027379 0.0036505
sun hours/day 0.024 1 1 0.0027379 0.0036505
kWh/(m2·y) 8.765813 365.2422 365.2422 1 1.333333
kWh/(kWp·y) 6.574360 273.9316 273.9316 0.75 1
at
Subscribe to: Posts (Atom)

Representation of a Lie group

From Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Representation_of_a_Lie_group...

  • Islamic State and the Levant
    From Wikipedia, the free encyclopedia Islamic State of Iraq and the Levant الدولة الإسلامية في العراق والشام   ( ...
  • Heart Sutra
    From Wikipedia, the free encyclopedia A reproduction of the palm -leaf manuscript in Siddham script ...
  • Slum
    From Wikipedia, the free encyclopedia ...