Argument maps are commonly used in the context of teaching and applying critical thinking. The purpose of mapping is to uncover the logical structure of arguments, identify unstated assumptions, evaluate the support an argument offers for a conclusion, and aid understanding of debates. Argument maps are often designed to support deliberation of issues, ideas and arguments in wicked problems.
An argument map is not to be confused with a concept map or a mind map, two other kinds of node–link diagram which have different constraints on nodes and links.
Key features
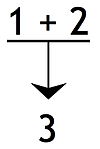
A number of different kinds of argument maps have been proposed but the most common, which Chris Reed and Glenn Rowe called the standard diagram, consists of a tree structure with each of the reasons leading to the conclusion. There is no consensus as to whether the conclusion should be at the top of the tree with the reasons leading up to it or whether it should be at the bottom with the reasons leading down to it. Another variation diagrams an argument from left to right.
According to Douglas N. Walton and colleagues, an argument map has two basic components: "One component is a set of circled numbers arrayed as points. Each number represents a proposition (premise or conclusion) in the argument being diagrammed. The other component is a set of lines or arrows joining the points. Each line (arrow) represents an inference. The whole network of points and lines represents a kind of overview of the reasoning in the given argument..." With the introduction of software for producing argument maps, it has become common for argument maps to consist of boxes containing the actual propositions rather than numbers referencing those propositions.
There is disagreement on the terminology to be used when describing argument maps, but the standard diagram contains the following structures:
Dependent premises or co-premises, where at least one of the joined premises requires another premise before it can give support to the conclusion: An argument with this structure has been called a linked argument.
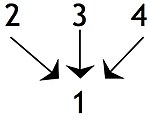
Independent premises, where the premise can support the conclusion on its own: Although independent premises may jointly make the conclusion more convincing, this is to be distinguished from situations where a premise gives no support unless it is joined to another premise. Where several premises or groups of premises lead to a final conclusion the argument might be described as convergent. This is distinguished from a divergent argument where a single premise might be used to support two separate conclusions.
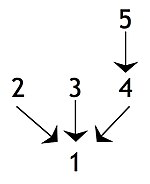
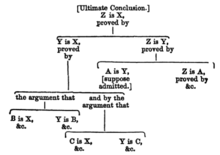
Intermediate conclusions or sub-conclusions, where a claim is supported by another claim that is used in turn to support some further claim, i.e. the final conclusion or another intermediate conclusion: In the following diagram, statement 4 is an intermediate conclusion in that it is a conclusion in relation to statement 5 but is a premise in relation to the final conclusion, i.e. statement 1. An argument with this structure is sometimes called a complex argument. If there is a single chain of claims containing at least one intermediate conclusion, the argument is sometimes described as a serial argument or a chain argument.
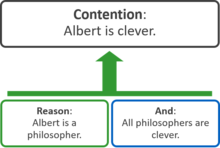
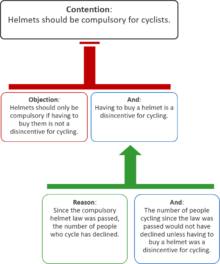
Each of these structures can be represented by the equivalent "box and line" approach to argument maps. In the following diagram, the contention is shown at the top, and the boxes linked to it represent supporting reasons, which comprise one or more premises. The green arrow indicates that the two reasons support the contention:
Argument maps can also represent counterarguments. In the following diagram, the two objections weaken the contention, while the reasons support the premise of the objection:
Representing an argument as an argument map
Diagramming written text
A written text can be transformed into an argument map by following a sequence of steps. Monroe Beardsley's 1950 book Practical Logic recommended the following procedure:
- Separate statements by brackets and number them.
- Put circles around the logical indicators.
- Supply, in parenthesis, any logical indicators that are left out.
- Set out the statements in a diagram in which arrows show the relationships between statements.
Beardsley gave the first example of a text being analysed in this way:
- Though ① [people who talk about the "social significance" of the arts don’t like to admit it], ② [music and painting are bound to suffer when they are turned into mere vehicles for propaganda]. For ③ [propaganda appeals to the crudest and most vulgar feelings]: (for) ④ [look at the academic monstrosities produced by the official Nazi painters]. What is more important, ⑤ [art must be an end in itself for the artist], because ⑥ [the artist can do the best work only in an atmosphere of complete freedom].
Beardsley said that the conclusion in this example is statement ②. Statement ④ needs to be rewritten as a declarative sentence, e.g. "Academic monstrosities [were] produced by the official Nazi painters." Statement ① points out that the conclusion isn't accepted by everyone, but statement ① is omitted from the diagram because it doesn't support the conclusion. Beardsley said that the logical relation between statement ③ and statement ④ is unclear, but he proposed to diagram statement ④ as supporting statement ③.
More recently, philosophy professor Maralee Harrell recommended the following procedure:
- Identify all the claims being made by the author.
- Rewrite them as independent statements, eliminating non-essential words.
- Identify which statements are premises, sub-conclusions, and the main conclusion.
- Provide missing, implied conclusions and implied premises. (This is optional depending on the purpose of the argument map.)
- Put the statements into boxes and draw a line between any boxes that are linked.
- Indicate support from premise(s) to (sub)conclusion with arrows.
Diagramming as thinking
Argument maps are useful not only for representing and analyzing existing writings, but also for thinking through issues as part of a problem-structuring process or writing process. The use of such argument analysis for thinking through issues has been called "reflective argumentation".
An argument map, unlike a decision tree, does not tell how to make a decision, but the process of choosing a coherent position (or reflective equilibrium) based on the structure of an argument map can be represented as a decision tree.
History
The philosophical origins and tradition of argument mapping
In the Elements of Logic, published in 1826 and issued in many subsequent editions, Archbishop Richard Whately gave probably the first form of an argument map, introducing it with the suggestion that "many students probably will find it a very clear and convenient mode of exhibiting the logical analysis of the course of argument, to draw it out in the form of a Tree, or Logical Division".
However, the technique did not become widely used, possibly because for complex arguments, it involved much writing and rewriting of the premises.
Legal philosopher and theorist John Henry Wigmore produced maps of legal arguments using numbered premises in the early 20th century, based in part on the ideas of 19th century philosopher Henry Sidgwick who used lines to indicate relations between terms.
Anglophone argument diagramming in the 20th century
Dealing with the failure of formal reduction of informal argumentation, English speaking argumentation theory developed diagrammatic approaches to informal reasoning over a period of fifty years.
Monroe Beardsley proposed a form of argument diagram in 1950. His method of marking up an argument and representing its components with linked numbers became a standard and is still widely used. He also introduced terminology that is still current describing convergent, divergent and serial arguments.
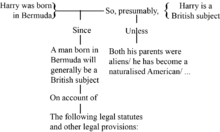
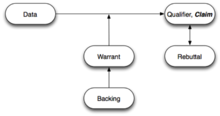
Stephen Toulmin, in his groundbreaking and influential 1958 book The Uses of Argument, identified several elements to an argument which have been generalized. The Toulmin diagram is widely used in educational critical teaching. Whilst Toulmin eventually had a significant impact on the development of informal logic he had little initial impact and the Beardsley approach to diagramming arguments along with its later developments became the standard approach in this field. Toulmin introduced something that was missing from Beardsley's approach. In Beardsley, "arrows link reasons and conclusions (but) no support is given to the implication itself between them. There is no theory, in other words, of inference distinguished from logical deduction, the passage is always deemed not controversial and not subject to support and evaluation". Toulmin introduced the concept of warrant which "can be considered as representing the reasons behind the inference, the backing that authorizes the link".
Beardsley's approach was refined by Stephen N. Thomas, whose 1973 book Practical Reasoning In Natural Language introduced the term linked to describe arguments where the premises necessarily worked together to support the conclusion. However, the actual distinction between dependent and independent premises had been made prior to this. The introduction of the linked structure made it possible for argument maps to represent missing or "hidden" premises. In addition, Thomas suggested showing reasons both for and against a conclusion with the reasons against being represented by dotted arrows. Thomas introduced the term argument diagram and defined basic reasons as those that were not supported by any others in the argument and the final conclusion as that which was not used to support any further conclusion.
Michael Scriven further developed the Beardsley-Thomas approach in his 1976 book Reasoning. Whereas Beardsley had said "At first, write out the statements...after a little practice, refer to the statements by number alone" Scriven advocated clarifying the meaning of the statements, listing them and then using a tree diagram with numbers to display the structure. Missing premises (unstated assumptions) were to be included and indicated with an alphabetical letter instead of a number to mark them off from the explicit statements. Scriven introduced counterarguments in his diagrams, which Toulmin had defined as rebuttal. This also enabled the diagramming of "balance of consideration" arguments.
In 1998 a series of large-scale argument maps released by Robert E. Horn stimulated widespread interest in argument mapping.
Development of computer-supported argument visualization
Human–computer interaction pioneer Douglas Engelbart, in a famous 1962 technical report on intelligence augmentation, envisioned in detail something like argument-mapping software as an integral part of future intelligence-augmenting computer interfaces:
You usually think of an argument as a serial sequence of steps of reason, beginning with known facts, assumptions, etc., and progressing toward a conclusion. Well, we do have to think through these steps serially, and we usually do list the steps serially when we write them out because that is pretty much the way our papers and books have to present them—they are pretty limiting in the symbol structuring they enable us to use. ... To help us get better comprehension of the structure of an argument, we can also call forth a schematic or graphical display. Once the antecedent-consequent links have been established, the computer can automatically construct such a display for us.
— Douglas Engelbart, "Augmenting human intellect: a conceptual framework" (1962)
In the middle to late 1980s, hypertext software applications that supported argument visualization were developed, including NoteCards and gIBIS; the latter generated an on-screen graphical hypertextual map of an issue-based information system, a model of argumentation developed by Werner Kunz and Horst Rittel in the 1970s. In the 1990s, Tim van Gelder and colleagues developed a series of software applications that permitted an argument map's premises to be fully stated and edited in the diagram, rather than in a legend. Van Gelder's first program, Reason!Able, was superseded by two subsequent programs, bCisive and Rationale.
Throughout the 1990s and 2000s, many other software applications were developed for argument visualization. By 2013, more than 60 such software systems existed. In a 2010 survey of computer-supported argumentation, Oliver Scheuer and colleagues noted that one of the differences between these software systems is whether collaboration is supported. In their survey, single-user argumentation systems included Convince Me, iLogos, LARGO, Athena, Araucaria, and Carneades; small group argumentation systems included Digalo, QuestMap, Compendium, Belvedere, and AcademicTalk; community argumentation systems included Debategraph and Collaboratorium.
Applications
Argument maps have been applied in many areas, but foremost in educational, academic and business settings, including design rationale. Argument maps are also used in forensic science, law, and artificial intelligence. It has also been proposed that argument mapping has a great potential to improve how we understand and execute democracy, in reference to the ongoing evolution of e-democracy.
Difficulties with the philosophical tradition
It has traditionally been hard to separate teaching critical thinking from the philosophical tradition of teaching logic and method, and most critical thinking textbooks have been written by philosophers. Informal logic textbooks are replete with philosophical examples, but it is unclear whether the approach in such textbooks transfers to non-philosophy students. There appears to be little statistical effect after such classes. Argument mapping, however, has a measurable effect according to many studies. For example, instruction in argument mapping has been shown to improve the critical thinking skills of business students.
Evidence that argument mapping improves critical thinking ability
There is empirical evidence that the skills developed in argument-mapping-based critical thinking courses substantially transfer to critical thinking done without argument maps. Alvarez's meta-analysis found that such critical thinking courses produced gains of around 0.70 SD, about twice as much as standard critical-thinking courses. The tests used in the reviewed studies were standard critical-thinking tests.
Limitations
When used with students in school, argument maps have limitations. They can "end up looking overly complex" and can increase cognitive load beyond what is optimal for learning the course content. Creating maps requires extensive coaching and feedback from an experienced argument mapper. Depending on the learning objectives, the time spent coaching students to create good maps may be better spent learning the course content instead of learning to diagram. When the goal is to prompt students to consider other perspectives and counterarguments, the goal may be more easily accomplished with other methods such as discussion, rubrics, and a simple argument framework or simple graphic organizer such as a vee diagram. To maximize the strengths of argument mapping and minimize its limitations in the classroom requires considering at what point in a learning progression the potential benefits of argument mapping would outweigh its potential disadvantages.
Standards
Argument Interchange Format
The Argument Interchange Format, AIF, is an international effort to develop a representational mechanism for exchanging argument resources between research groups, tools, and domains using a semantically rich language. AIF-RDF is the extended ontology represented in the Resource Description Framework Schema (RDFS) semantic language. Though AIF is still something of a moving target, it is settling down.
Legal Knowledge Interchange Format
The Legal Knowledge Interchange Format (LKIF) was developed in the European ESTRELLA project and designed with the goal of becoming a standard for representing and interchanging policy, legislation and cases, including their justificatory arguments, in the legal domain. LKIF builds on and uses the Web Ontology Language (OWL) for representing concepts and includes a reusable basic ontology of legal concepts.
Argdown
Argdown is a Markdown-inspired lightweight markup language for complex argumentation. It is intended for exchanging arguments and argument reconstructions in a universally accessible and highly human-readable way. The Argdown syntax is accompanied by tools that facilitate coding and transform Argdown documents into argument maps.