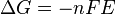From Wikipedia, the free encyclopedia
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature. The negative of the difference in the Helmholtz energy is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. If the volume is not held constant, part of this work will be performed as boundary work. The Helmholtz energy is commonly used for systems held at constant volume. Since in this case no work is performed on the environment, the drop in the Helmholtz energy is equal to the maximum amount of useful work that can be extracted from the system. For a system at constant temperature and volume, the Helmholtz energy is minimized at equilibrium.
The Helmholtz free energy was developed by Hermann von Helmholtz, a German physicist, and is usually denoted by the letter A (from the German “Arbeit” or work), or the letter F . The IUPAC recommends the letter A as well as the use of name Helmholtz energy.[1] In physics, the letter F can also be used to denote the Helmholtz energy, as Helmholtz energy is sometimes referred to as the Helmholtz function, Helmholtz free energy, or simply free energy (not to be confused with Gibbs free energy).
While Gibbs free energy is most commonly used as a measure of thermodynamic potential, especially in the field of chemistry, it is inconvenient for some applications that do not occur at constant pressure. For example, in explosives research, Helmholtz free energy is often used since explosive reactions by their nature induce pressure changes. It is also frequently used to define fundamental equations of state of pure substances.
 is the internal energy,
is the internal energy,  is the energy added by heating and
is the energy added by heating and 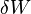 is the work done by the system. From the second law of thermodynamics, for a reversible process we may say that
is the work done by the system. From the second law of thermodynamics, for a reversible process we may say that  . Also, in case of a reversible change, the work done can be expressed as
. Also, in case of a reversible change, the work done can be expressed as 
The expression for the internal energy becomes
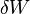 becomes dW) . dW includes all reversible work, mechanical (pressure-volume) work and non-mechanical work (e. g. electrical work).
becomes dW) . dW includes all reversible work, mechanical (pressure-volume) work and non-mechanical work (e. g. electrical work).
The maximum energy that can be freed for work is the negative of the change in A. The process is nominally isothermal, but it is only required that the system has the same initial and final temperature, and not that the temperature stays constant along the process.
Now, imagine that our system is also kept at constant volume to prevent work from being done. If temperature and volume are kept constant, then dA = 0; this is a necessary, but not sufficient condition for equilibrium. For any spontaneous process, the change in Helmholtz free energy must be negative, that is . Therefore, to prevent a spontaneous change, we must also require that A be at a minimum.
. Therefore, to prevent a spontaneous change, we must also require that A be at a minimum.
Since the thermodynamical variables of the system are well defined in the initial state and the final state, the internal energy increase, , the entropy increase
, the entropy increase  , and the total amount of work that can be extracted, performed by the system,
, and the total amount of work that can be extracted, performed by the system,  , are well-defined quantities. Conservation of energy implies:
, are well-defined quantities. Conservation of energy implies:
This result seems to contradict the equation , as keeping T and V constant seems to imply
, as keeping T and V constant seems to imply 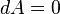 and hence
and hence  . In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that
. In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that  where the
where the  are different thermodynamic functions of state.
are different thermodynamic functions of state.
One can imagine that the spontaneous change is carried out in a sequence of infinitesimally small steps. To describe such a system thermodynamically, one needs to enlarge the thermodynamical state space of the system. In case of a chemical reaction, one must specify the number of particles of each type. The differential of the free energy then generalizes to:
 are the numbers of particles of type j and the
are the numbers of particles of type j and the 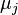 are the corresponding chemical potentials. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.
are the corresponding chemical potentials. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.
In case there are other external parameters the above equation generalizes to:
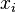 are the external variables and the
are the external variables and the  the corresponding generalized forces.
the corresponding generalized forces.
The average internal energy of the system is the expectation value of the energy and can be expressed in terms of Z as follows:
 . Then changing the system's temperature parameter by
. Then changing the system's temperature parameter by 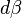 and the external variable by
and the external variable by 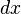 will lead to a change in
will lead to a change in  :
:
 as:
as:
 where
where 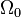 is the ground state degeneracy. The partition function in this limit is
is the ground state degeneracy. The partition function in this limit is  where
where  is the ground state energy. Thus, we see that
is the ground state energy. Thus, we see that  and that:
and that:
Suppose we replace the real Hamiltonian of the model by a trial Hamiltonian
of the model by a trial Hamiltonian  , which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
, which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
 , then
, then
 is the free energy of the original Hamiltonian and
is the free energy of the original Hamiltonian and  is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
The Bogoliubov inequality is often formulated in a slightly different but equivalent way. If we write the Hamiltonian as:
 is exactly solvable, then we can apply the above inequality by defining
is exactly solvable, then we can apply the above inequality by defining
 to be the average of X over the canonical ensemble defined by
to be the average of X over the canonical ensemble defined by  . Since
. Since  defined this way differs from
defined this way differs from  by a constant, we have in general
by a constant, we have in general
 is the free energy of the model defined by
is the free energy of the model defined by  plus
plus  . This means that
. This means that
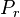 and
and 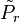 , respectively. The inequality:
, respectively. The inequality:
We can write the inequality as:
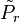 . If we now substitute in here the expressions for the probability distributions:
. If we now substitute in here the expressions for the probability distributions:
 and
and  are, by assumption, identical we have:
are, by assumption, identical we have:
We can easily generalize this proof to the case of quantum mechanical models. We denote the eigenstates of by
by 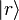 . We denote the diagonal components of the density matrices for the canonical distributions for
. We denote the diagonal components of the density matrices for the canonical distributions for  and
and  in this basis as:
in this basis as:
 are the eigenvalues of
are the eigenvalues of 
We assume again that the averages of H and in the canonical ensemble defined by
in the canonical ensemble defined by  are the same:
are the same:
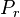 and the
and the 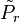 sum to 1. On the l.h.s. we can replace:
sum to 1. On the l.h.s. we can replace:
 are the same then leads to the same conclusion as in the classical case:
are the same then leads to the same conclusion as in the classical case:
 ) must be replaced by the product of volume, stress, and an infinitesimal strain:[3]
) must be replaced by the product of volume, stress, and an infinitesimal strain:[3]
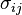 is the stress tensor, and
is the stress tensor, and  is the strain tensor. In the case of linear elastic materials that obey Hooke's Law, the stress is related to the strain by:
is the strain tensor. In the case of linear elastic materials that obey Hooke's Law, the stress is related to the strain by:
 to obtain the Helmholtz energy:
to obtain the Helmholtz energy:
The Helmholtz free energy was developed by Hermann von Helmholtz, a German physicist, and is usually denoted by the letter A (from the German “Arbeit” or work), or the letter F . The IUPAC recommends the letter A as well as the use of name Helmholtz energy.[1] In physics, the letter F can also be used to denote the Helmholtz energy, as Helmholtz energy is sometimes referred to as the Helmholtz function, Helmholtz free energy, or simply free energy (not to be confused with Gibbs free energy).
While Gibbs free energy is most commonly used as a measure of thermodynamic potential, especially in the field of chemistry, it is inconvenient for some applications that do not occur at constant pressure. For example, in explosives research, Helmholtz free energy is often used since explosive reactions by their nature induce pressure changes. It is also frequently used to define fundamental equations of state of pure substances.
Definition
The Helmholtz energy is defined as:[2]- A is the Helmholtz free energy (SI: joules, CGS: ergs),
- U is the internal energy of the system (SI: joules, CGS: ergs),
- T is the absolute temperature (kelvins),
- S is the entropy (SI: joules per kelvin, CGS: ergs per kelvin).
Mathematical development
From the first law of thermodynamics (with a constant number of particles) we have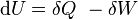 ,
,
 is the internal energy,
is the internal energy,  is the energy added by heating and
is the energy added by heating and 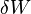 is the work done by the system. From the second law of thermodynamics, for a reversible process we may say that
is the work done by the system. From the second law of thermodynamics, for a reversible process we may say that  . Also, in case of a reversible change, the work done can be expressed as
. Also, in case of a reversible change, the work done can be expressed as 
 ,
,
Work in an Isothermal Process and Equilibrium Conditions
The fundamental thermodynamic relation isThe expression for the internal energy becomes
 (isothermal process)
(isothermal process)
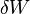 becomes dW) . dW includes all reversible work, mechanical (pressure-volume) work and non-mechanical work (e. g. electrical work).
becomes dW) . dW includes all reversible work, mechanical (pressure-volume) work and non-mechanical work (e. g. electrical work).The maximum energy that can be freed for work is the negative of the change in A. The process is nominally isothermal, but it is only required that the system has the same initial and final temperature, and not that the temperature stays constant along the process.
Now, imagine that our system is also kept at constant volume to prevent work from being done. If temperature and volume are kept constant, then dA = 0; this is a necessary, but not sufficient condition for equilibrium. For any spontaneous process, the change in Helmholtz free energy must be negative, that is
 . Therefore, to prevent a spontaneous change, we must also require that A be at a minimum.
. Therefore, to prevent a spontaneous change, we must also require that A be at a minimum.Minimum free energy and maximum work principles
The laws of thermodynamics are only directly applicable to systems in thermal equilibrium. If we wish to describe phenomena like chemical reactions, then the best we can do is to consider suitably chosen initial and final states in which the system is in (metastable) thermal equilibrium. If the system is kept at fixed volume and is in contact with a heat bath at some constant temperature, then we can reason as follows.Since the thermodynamical variables of the system are well defined in the initial state and the final state, the internal energy increase,
 , the entropy increase
, the entropy increase  , and the total amount of work that can be extracted, performed by the system,
, and the total amount of work that can be extracted, performed by the system,  , are well-defined quantities. Conservation of energy implies:
, are well-defined quantities. Conservation of energy implies:This result seems to contradict the equation
 , as keeping T and V constant seems to imply
, as keeping T and V constant seems to imply 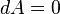 and hence
and hence  . In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that
. In reality there is no contradiction. After the spontaneous change, the system, as described by thermodynamics, is a different system with a different free energy function than it was before the spontaneous change. Thus, we can say that  where the
where the  are different thermodynamic functions of state.
are different thermodynamic functions of state.One can imagine that the spontaneous change is carried out in a sequence of infinitesimally small steps. To describe such a system thermodynamically, one needs to enlarge the thermodynamical state space of the system. In case of a chemical reaction, one must specify the number of particles of each type. The differential of the free energy then generalizes to:
 are the numbers of particles of type j and the
are the numbers of particles of type j and the 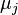 are the corresponding chemical potentials. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.
are the corresponding chemical potentials. This equation is then again valid for both reversible and non-reversible changes. In case of a spontaneous change at constant T and V, the last term will thus be negative.In case there are other external parameters the above equation generalizes to:
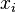 are the external variables and the
are the external variables and the  the corresponding generalized forces.
the corresponding generalized forces.Relation to the canonical partition function
A system kept at constant volume, temperature, and particle number is described by the canonical ensemble. The probability to find the system in some energy eigenstate r is given by:The average internal energy of the system is the expectation value of the energy and can be expressed in terms of Z as follows:
 . Then changing the system's temperature parameter by
. Then changing the system's temperature parameter by 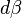 and the external variable by
and the external variable by 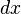 will lead to a change in
will lead to a change in  :
: as:
as: where
where 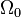 is the ground state degeneracy. The partition function in this limit is
is the ground state degeneracy. The partition function in this limit is  where
where  is the ground state energy. Thus, we see that
is the ground state energy. Thus, we see that  and that:
and that:Bogoliubov inequality
Computing the free energy is an intractable problem for all but the simplest models in statistical physics. A powerful approximation method is mean field theory, which is a variational method based on the Bogoliubov inequality. This inequality can be formulated as follows.Suppose we replace the real Hamiltonian
 of the model by a trial Hamiltonian
of the model by a trial Hamiltonian  , which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that
, which has different interactions and may depend on extra parameters that are not present in the original model. If we choose this trial Hamiltonian such that , then
, then is the free energy of the original Hamiltonian and
is the free energy of the original Hamiltonian and  is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.
is the free energy of the trial Hamiltonian. By including a large number of parameters in the trial Hamiltonian and minimizing the free energy we can expect to get a close approximation to the exact free energy.The Bogoliubov inequality is often formulated in a slightly different but equivalent way. If we write the Hamiltonian as:
 is exactly solvable, then we can apply the above inequality by defining
is exactly solvable, then we can apply the above inequality by defining to be the average of X over the canonical ensemble defined by
to be the average of X over the canonical ensemble defined by  . Since
. Since  defined this way differs from
defined this way differs from  by a constant, we have in general
by a constant, we have in general is the free energy of the model defined by
is the free energy of the model defined by  plus
plus  . This means that
. This means thatProof
For a classical model we can prove the Bogoliubov inequality as follows. We denote the canonical probability distributions for the Hamiltonian and the trial Hamiltonian by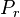 and
and 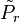 , respectively. The inequality:
, respectively. The inequality:We can write the inequality as:
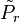 . If we now substitute in here the expressions for the probability distributions:
. If we now substitute in here the expressions for the probability distributions: and
and  are, by assumption, identical we have:
are, by assumption, identical we have:We can easily generalize this proof to the case of quantum mechanical models. We denote the eigenstates of
 by
by 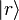 . We denote the diagonal components of the density matrices for the canonical distributions for
. We denote the diagonal components of the density matrices for the canonical distributions for  and
and  in this basis as:
in this basis as: are the eigenvalues of
are the eigenvalues of 
We assume again that the averages of H and
 in the canonical ensemble defined by
in the canonical ensemble defined by  are the same:
are the same: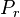 and the
and the 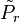 sum to 1. On the l.h.s. we can replace:
sum to 1. On the l.h.s. we can replace: are the same then leads to the same conclusion as in the classical case:
are the same then leads to the same conclusion as in the classical case:Generalized Helmholtz energy
In the more general case, the mechanical term ( ) must be replaced by the product of volume, stress, and an infinitesimal strain:[3]
) must be replaced by the product of volume, stress, and an infinitesimal strain:[3]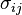 is the stress tensor, and
is the stress tensor, and  is the strain tensor. In the case of linear elastic materials that obey Hooke's Law, the stress is related to the strain by:
is the strain tensor. In the case of linear elastic materials that obey Hooke's Law, the stress is related to the strain by: to obtain the Helmholtz energy:
to obtain the Helmholtz energy: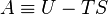
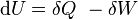 ,
,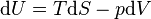
 ,
,





 (isothermal process)
(isothermal process)
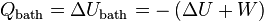







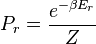














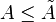


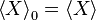





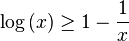


![P_{r}=\frac{\exp\left[-\beta H\left(r\right)\right]}{Z}\,](http://upload.wikimedia.org/math/5/d/2/5d21c9e5be02a1b14c0c32b6ea517d50.png)
![\tilde{P}_{r}=\frac{\exp\left[-\beta\tilde{H}\left(r\right)\right]}{\tilde{Z}}\,](http://upload.wikimedia.org/math/e/5/5/e55b932bbdfd68e905e27d0715f36a22.png)
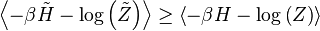

![P_{r}=\left\langle r\left|\frac{\exp\left[-\beta H\right]}{Z}\right|r\right\rangle\,](http://upload.wikimedia.org/math/c/1/3/c134d454990cfb0d8a3d392796f4e2ef.png)
![\tilde{P}_{r}=\left\langle r\left|\frac{\exp\left[-\beta\tilde{H}\right]}{\tilde{Z}}\right|r\right\rangle=\frac{\exp\left(-\beta\tilde{E}_{r}\right)}{\tilde{Z}}\,](http://upload.wikimedia.org/math/f/8/d/f8dc0d4f04021c2fb9b0b77a5a498adb.png)
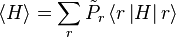
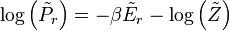

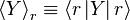
![\log\left[\left\langle\exp\left(X\right)\right\rangle_{r}\right]\geq\left\langle X\right\rangle_{r}\,](http://upload.wikimedia.org/math/3/1/3/313d7ba7a25528c08240d40cbc98ebf4.png)
![\log\left(P_{r}\right)=\log\left[\left\langle\exp\left(-\beta H - \log\left(Z\right)\right)\right\rangle_{r}\right]\geq\left\langle -\beta H - \log\left(Z\right)\right\rangle_{r}\,](http://upload.wikimedia.org/math/b/c/b/bcb635db154784912155f10a34df24d6.png)



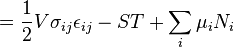







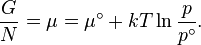
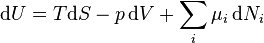 .
. .
.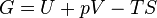 .
. .
.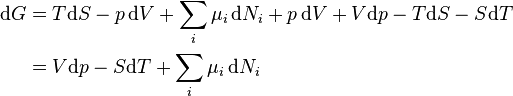 .
. .
.
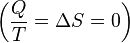 process.
process. .
.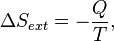 corresponds to the entropy change of the surroundings.
corresponds to the entropy change of the surroundings.



 (eq.1)
(eq.1) favoured reaction (Spontaneous)
favoured reaction (Spontaneous) Neither the forward nor the reverse reaction prevails (
Neither the forward nor the reverse reaction prevails ( disfavoured reaction (Nonspontaneous)
disfavoured reaction (Nonspontaneous) (eq.2)
(eq.2)

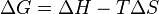 (for constant temperature)
(for constant temperature) (for a system at equilibrium)
(for a system at equilibrium) (see
(see