Nash equilibrium

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Nash_equilibrium 

 

Nash equilibrium

In game theory, a Nash equilibrium is a situation where no player could gain more by changing their own strategy (holding all other players' strategies fixed) in a game. Nash equilibrium is the most commonly used solution concept for non-cooperative games.

If each player has chosen a strategy – an action plan based on what has happened so far in the game – and no one can increase one's own expected payoff by changing one's strategy while the other players keep theirs unchanged, then the current set of strategy choices constitutes a Nash equilibrium.

If two players Alice and Bob choose strategies A and B, (A, B) is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and Bob has no other strategy available that does better than B at maximizing his payoff in response to Alice choosing A. In a game in which Carol and Dan are also players, (A, B, C, D) is a Nash equilibrium if A is Alice's best response to (B, C, D), B is Bob's best response to (A, C, D), and so forth.

The idea of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to his model of competition in an oligopoly. John Nash showed that there is a Nash equilibrium, possibly in mixed strategies, for every finite game.

Applications

Game theorists use Nash equilibrium to analyze the outcome of the strategic interaction of several decision makers. In a strategic interaction, the outcome for each decision-maker depends on the decisions of the others as well as their own. The simple insight underlying Nash's idea is that one cannot predict the choices of multiple decision makers if one analyzes those decisions in isolation. Instead, one must ask what each player would do taking into account what the player expects the others to do. Nash equilibrium is achieved when no player can improve their outcome by changing their decision, assuming the other players' choices remain unchanged.

The concept has been used to analyze hostile situations such as wars and arms races (see prisoner's dilemma), and also how conflict may be mitigated by repeated interaction (see tit-for-tat). It has also been used to study to what extent people with different preferences can cooperate (see battle of the sexes), and whether they will take risks to achieve a cooperative outcome (see stag hunt). It has been used to study the adoption of technical standards, and also the occurrence of bank runs and currency crises (see coordination game). Other applications include traffic flow (see Wardrop's principle), how to organize auctions (see auction theory), the outcome of efforts exerted by multiple parties in the education process, regulatory legislation such as environmental regulations (see tragedy of the commons), natural resource management, analysing strategies in marketing, penalty kicks in football (I.e. soccer; see matching pennies), robot navigation in crowds, energy systems, transportation systems, evacuation problems and wireless communications.

History

Nash equilibrium is named after American mathematician John Forbes Nash Jr. The same idea was used in a particular application in 1838 by Antoine Augustin Cournot in his theory of oligopoly. In Cournot's theory, each of several firms choose how much output to produce to maximize its profit. The best output for one firm depends on the outputs of the others. A Cournot equilibrium occurs when each firm's output maximizes its profits given the output of the other firms, which is a pure-strategy Nash equilibrium. Cournot also introduced the concept of best response dynamics in his analysis of the stability of equilibrium. Cournot did not use the idea in any other applications, however, or define it generally.

The modern concept of Nash equilibrium is instead defined in terms of mixed strategies, where players choose a probability distribution over possible pure strategies (which might put 100% of the probability on one pure strategy; such pure strategies are a subset of mixed strategies). The concept of a mixed-strategy equilibrium was introduced by John von Neumann and Oskar Morgenstern in their 1944 book The Theory of Games and Economic Behavior, but their analysis was restricted to the special case of zero-sum games. They showed that a mixed-strategy Nash equilibrium will exist for any zero-sum game with a finite set of actions. The contribution of Nash in his 1951 article "Non-Cooperative Games" was to define a mixed-strategy Nash equilibrium for any game with a finite set of actions and prove that at least one (mixed-strategy) Nash equilibrium must exist in such a game. The key to Nash's ability to prove existence far more generally than von Neumann lay in his definition of equilibrium. According to Nash, "an equilibrium point is an n-tuple such that each player's mixed strategy maximizes [their] payoff if the strategies of the others are held fixed. Thus each player's strategy is optimal against those of the others." Putting the problem in this framework allowed Nash to employ the Kakutani fixed-point theorem in his 1950 paper to prove existence of equilibria. His 1951 paper used the simpler Brouwer fixed-point theorem for the same purpose.

Game theorists have discovered that in some circumstances Nash equilibrium makes invalid predictions or fails to make a unique prediction. They have proposed many solution concepts ('refinements' of Nash equilibria) designed to rule out implausible Nash equilibria. One particularly important issue is that some Nash equilibria may be based on threats that are not 'credible'. In 1965 Reinhard Selten proposed subgame perfect equilibrium as a refinement that eliminates equilibria which depend on non-credible threats. Other extensions of the Nash equilibrium concept have addressed what happens if a game is repeated, or what happens if a game is played in the absence of complete information. However, subsequent refinements and extensions of Nash equilibrium share the main insight on which Nash's concept rests: the equilibrium is a set of strategies such that each player's strategy is optimal given the choices of the others.

Definitions

A strategy profile is a set of strategies, one for each player. Informally, a strategy profile is a Nash equilibrium if no player can do better by unilaterally changing their strategy. To see what this means, imagine that each player is told the strategies of the others. Suppose then that each player asks themselves: "Knowing the strategies of the other players, and treating the strategies of the other players as set in stone, can I benefit by changing my strategy?"

For instance if a player prefers "Yes", then that set of strategies is not a Nash equilibrium. But if every player prefers not to switch (or is indifferent between switching and not) then the strategy profile is a Nash equilibrium. Thus, each strategy in a Nash equilibrium is a best response to the other players' strategies in that equilibrium.

Formally, let ${\displaystyle S_i}$ be the set of all possible strategies for player ${\displaystyle i}$, where ${\displaystyle i=1,\dots ,N}$. Let ${\displaystyle s^{\ast }=(s_i^{\ast },s_{-i}^{\ast })}$ be a strategy profile, a set consisting of one strategy for each player, where ${\displaystyle s_{-i}^{\ast }}$ denotes the ${\displaystyle N-1}$ strategies of all the players except ${\displaystyle i}$. Let ${\displaystyle u_i(s_i,s_{-i}^{\ast })}$ be player i's payoff as a function of the strategies. The strategy profile ${\displaystyle s^{\ast }}$ is a Nash equilibrium if $${\displaystyle u_i(s_i^{\ast },s_{-i}^{\ast })\ge u_i(s_i,s_{-i}^{\ast })\text{for all}{s}_i\in S_i.}$$

A game can have more than one Nash equilibrium. Even if the equilibrium is unique, it might be weak: a player might be indifferent among several strategies given the other players' choices. It is unique and called a strict Nash equilibrium if the inequality is strict so one strategy is the unique best response: $${\displaystyle u_i(s_i^{\ast },s_{-i}^{\ast })>u_i(s_i,s_{-i}^{\ast })\text{for all}{s}_i\in S_i,s_i\ne s_i^{\ast }.}$$

The strategy set ${\displaystyle S_i}$ can be different for different players, and its elements can be a variety of mathematical objects. Most simply, a player might choose between two strategies, e.g. ${\displaystyle S_i=\{\text{Yes},\text{No}\}.}$ Or the strategy set might be a finite set of conditional strategies responding to other players, e.g. ${\displaystyle S_i=\{\text{Yes}\mid p=\text{Low},\text{No}\mid p=\text{High}\}.}$ Or it might be an infinite set, a continuum or unbounded, e.g. ${\displaystyle S_i=\{\text{Price}\}}$ such that ${\displaystyle \text{Price}}$ is a non-negative real number. Nash's existing proofs assume a finite strategy set, but the concept of Nash equilibrium does not require it.

Variants

Pure/mixed equilibrium

A game can have a pure-strategy or a mixed-strategy Nash equilibrium. In the latter, not every player always plays the same strategy. Instead, there is a probability distribution over different strategies.

Strict/non-strict equilibrium

Suppose that in the Nash equilibrium, each player asks themselves: "Knowing the strategies of the other players, and treating the strategies of the other players as set in stone, would I suffer a loss by changing my strategy?"

If every player's answer is "Yes", then the equilibrium is classified as a strict Nash equilibrium.

If instead, for some player, there is exact equality between the strategy in Nash equilibrium and some other strategy that gives exactly the same payout (i.e. the player is indifferent between switching and not), then the equilibrium is classified as a weak or non-strict Nash equilibrium.

Equilibria for coalitions

The Nash equilibrium defines stability only in terms of individual player deviations. In cooperative games such a concept is not convincing enough. Strong Nash equilibrium allows for deviations by every conceivable coalition. Formally, a strong Nash equilibrium is a Nash equilibrium in which no coalition, taking the actions of its complements as given, can cooperatively deviate in a way that benefits all of its members. However, the strong Nash concept is sometimes perceived as too "strong" in that the environment allows for unlimited private communication. In fact, strong Nash equilibrium has to be weakly Pareto efficient. As a result of these requirements, strong Nash is too rare to be useful in many branches of game theory. However, in games such as elections with many more players than possible outcomes, it can be more common than a stable equilibrium.

A refined Nash equilibrium known as coalition-proof Nash equilibrium (CPNE) occurs when players cannot do better even if they are allowed to communicate and make "self-enforcing" agreement to deviate. Every correlated strategy supported by iterated strict dominance and on the Pareto frontier is a CPNE. Further, it is possible for a game to have a Nash equilibrium that is resilient against coalitions less than a specified size, k. CPNE is related to the theory of the core.

Existence

Nash proved that if mixed strategies (where a player chooses probabilities of using various pure strategies) are allowed, then every game with a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium, which might be a pure strategy for each player or might be a probability distribution over strategies for each player.

Nash equilibria need not exist if the set of choices is infinite and non-compact. For example:

• A game where two players simultaneously name a number and the player naming the larger number wins does not have a NE, as the set of choices is not compact because it is unbounded.
• Each of two players chooses a real number strictly less than 5 and the winner is whoever has the biggest number; no biggest number strictly less than 5 exists (if the number could equal 5, the Nash equilibrium would have both players choosing 5 and tying the game). Here, the set of choices is not compact because it is not closed.

However, a Nash equilibrium exists if the set of choices is compact with each player's payoff continuous in the strategies of all the players.

Generalizations

Nash's existence theorem has been extended to more general classes of games.

Games with coupled constraints

In Nash's model, the set of strategies available to each player is fixed and does not depend on the other players' strategies. A more general model allows these sets to depend on other players' strategies; this is often called coupled constraints. In Nash's model, the set of possible strategy-profiles is a Cartesian product of the players' strategy sets, whereas in the more general model it can be an arbitrary set. When there are coupled constraints, the equilibrium is often called Generalized Nash equilibrium (GNE).

Rosen proved that, if the set of strategy-profiles is any convex set, and the utility function of each player is continuous in all strategies and a concave function of the player's own strategy, then a GNE exists; see concave games.

Non-atomic games

Nash considered games with finitely many players, in non-atomic games the set of players is infinite - there is a continuum of players David Schmeidler proved that an equilibrium exists under certain conditions.

Rationality

The Nash equilibrium may sometimes appear non-rational in a third-person perspective. This is because a Nash equilibrium is not necessarily Pareto optimal.

Nash equilibrium may also have non-rational consequences in sequential games because players may "threaten" each other with threats they would not actually carry out. For such games the subgame perfect Nash equilibrium may be more meaningful as a tool of analysis.

Examples

Coordination game

Main article: Coordination game

 

A coordination game showing payoffs for player 1 (row) and player 2 (column)

Player 1 strategy	Player 2 strategy
	A	B
A	4 4	3 1
B	1 3	2 2

The coordination game is a classic two-player, two-strategy game, as shown in the example payoff matrix to the right. There are two pure-strategy equilibria, (A,A) with payoff 4 for each player and (B,B) with payoff 2 for each. The combination (B,B) is a Nash equilibrium because if either player unilaterally changes their strategy from B to A, their payoff will fall from 2 to 1.

The stag hunt

Player 1 strategy	Player 2 strategy
	Hunt stag	Hunt rabbit
Hunt stag	2 2	1 0
Hunt rabbit	0 1	1 1

A famous example of a coordination game is the stag hunt. Two players may choose to hunt a stag or a rabbit, the stag providing more meat (4 utility units, 2 for each player) than the rabbit (1 utility unit). The caveat is that the stag must be cooperatively hunted, so if one player attempts to hunt the stag, while the other hunts the rabbit, the stag hunter will totally fail, for a payoff of 0, whereas the rabbit hunter will succeed, for a payoff of 1. The game has two equilibria, (stag, stag) and (rabbit, rabbit), because a player's optimal strategy depends on their expectation on what the other player will do. If one hunter trusts that the other will hunt the stag, they should hunt the stag; however if they think the other will hunt the rabbit, they too will hunt the rabbit. This game is used as an analogy for social cooperation, since much of the benefit that people gain in society depends upon people cooperating and implicitly trusting one another to act in a manner corresponding with cooperation.

Driving on a road against an oncoming car, and having to choose either to swerve on the left or to swerve on the right of the road, is also a coordination game. For example, with payoffs 10 meaning no crash and 0 meaning a crash, the coordination game can be defined with the following payoff matrix:

The driving game

Player 1 strategy	Player 2 strategy
	Drive on the left	Drive on the right
Drive on the left	10 10	0 0
Drive on the right	0 0	10 10

In this case there are two pure-strategy Nash equilibria, when both choose to either drive on the left or on the right. If we admit mixed strategies (where a pure strategy is chosen at random, subject to some fixed probability), then there are three Nash equilibria for the same case: two we have seen from the pure-strategy form, where the probabilities are (0%, 100%) for player one, (0%, 100%) for player two; and (100%, 0%) for player one, (100%, 0%) for player two respectively. We add another where the probabilities for each player are (50%, 50%).

Network traffic

See also: Braess's paradox

Sample network graph. Values on edges are the travel time experienced by a "car" traveling down that edge. ${\displaystyle x}$ is the number of cars traveling via that edge.

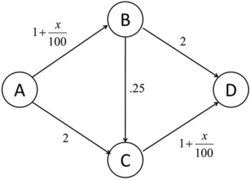
An application of Nash equilibria is in determining the expected flow of traffic in a network. Consider the graph on the right. If we assume that there are ${\displaystyle x}$ "cars" traveling from A to D, what is the expected distribution of traffic in the network?

This situation can be modeled as a "game", where every traveler has a choice of 3 strategies and where each strategy is a route from A to D (one of ABD, ABCD, or ACD). The "payoff" of each strategy is the travel time of each route. In the graph on the right, a car travelling via ABD experiences travel time of ${\displaystyle 1+\frac{x}{100}+2}$, where ${\displaystyle x}$ is the number of cars traveling on edge AB. Thus, payoffs for any given strategy depend on the choices of the other players, as is usual. However, the goal, in this case, is to minimize travel time, not maximize it. Equilibrium will occur when the time on all paths is exactly the same. When that happens, no single driver has any incentive to switch routes, since it can only add to their travel time. For the graph on the right, if, for example, 100 cars are travelling from A to D, then equilibrium will occur when 25 drivers travel via ABD, 50 via ABCD, and 25 via ACD. Every driver now has a total travel time of 3.75 (to see this, a total of 75 cars take the AB edge, and likewise, 75 cars take the CD edge).

Notice that this distribution is not, actually, socially optimal. If the 100 cars agreed that 50 travel via ABD and the other 50 through ACD, then travel time for any single car would actually be 3.5, which is less than 3.75. This is also the Nash equilibrium if the path between B and C is removed, which means that adding another possible route can decrease the efficiency of the system, a phenomenon known as Braess's paradox.

Competition game

A competition game

Player 1 strategy	Player 2 strategy
	Choose "0"	Choose "1"	Choose "2"	Choose "3"
Choose "0"	0, 0	2, −2	2, −2	2, −2
Choose "1"	−2, 2	1, 1	3, −1	3, −1
Choose "2"	−2, 2	−1, 3	2, 2	4, 0
Choose "3"	−2, 2	−1, 3	0, 4	3, 3

This can be illustrated by a two-player game in which both players simultaneously choose an integer from 0 to 3 and they both win the smaller of the two numbers in points. In addition, if one player chooses a larger number than the other, then they have to give up two points to the other.

This game has a unique pure-strategy Nash equilibrium: both players choosing 0 (highlighted in light red). Any other strategy can be improved by a player switching their number to one less than that of the other player. In the adjacent table, if the game begins at the green square, it is in player 1's interest to move to the purple square and it is in player 2's interest to move to the blue square. Although it would not fit the definition of a competition game, if the game is modified so that the two players win the named amount if they both choose the same number, and otherwise win nothing, then there are 4 Nash equilibria: (0,0), (1,1), (2,2), and (3,3).

Nash equilibria in a payoff matrix

There is an easy numerical way to identify Nash equilibria on a payoff matrix. It is especially helpful in two-person games where players have more than two strategies. In this case formal analysis may become too long. This rule does not apply to the case where mixed (stochastic) strategies are of interest. The rule goes as follows: if the first payoff number, in the payoff pair of the cell, is the maximum of the column of the cell and if the second number is the maximum of the row of the cell – then the cell represents a Nash equilibrium.

We can apply this rule to a 3×3 matrix:

A payoff matrix – Nash equilibria in bold

Player 1 strategy	Player 2 strategy
	Option A	Option B	Option C
Option A	0, 0	25, 40	5, 10
Option B	40, 25	0, 0	5, 15
Option C	10, 5	15, 5	10, 10

Using the rule, we can very quickly (much faster than with formal analysis) see that the Nash equilibria cells are (B,A), (A,B), and (C,C). Indeed, for cell (B,A), 40 is the maximum of the first column and 25 is the maximum of the second row. For (A,B), 25 is the maximum of the second column and 40 is the maximum of the first row; the same applies for cell (C,C). For other cells, either one or both of the duplet members are not the maximum of the corresponding rows and columns.

This said, the actual mechanics of finding equilibrium cells is obvious: find the maximum of a column and check if the second member of the pair is the maximum of the row. If these conditions are met, the cell represents a Nash equilibrium. Check all columns this way to find all NE cells. An N×N matrix may have between 0 and N×N pure-strategy Nash equilibria.

Stability

The concept of stability, useful in the analysis of many kinds of equilibria, can also be applied to Nash equilibria.

A Nash equilibrium for a mixed-strategy game is stable if a small change (specifically, an infinitesimal change) in probabilities for one player leads to a situation where two conditions hold:

1. the player who did not change has no better strategy in the new circumstance
2. the player who did change is now playing with a strictly worse strategy.

If these cases are both met, then a player with the small change in their mixed strategy will return immediately to the Nash equilibrium. The equilibrium is said to be stable. If condition one does not hold then the equilibrium is unstable. If only condition one holds then there are likely to be an infinite number of optimal strategies for the player who changed.

In the "driving game" example above there are both stable and unstable equilibria. The equilibria involving mixed strategies with 100% probabilities are stable. If either player changes their probabilities slightly, they will be both at a disadvantage, and their opponent will have no reason to change their strategy in turn. The (50%,50%) equilibrium is unstable. If either player changes their probabilities (which would neither benefit or damage the expectation of the player who did the change, if the other player's mixed strategy is still (50%,50%)), then the other player immediately has a better strategy at either (0%, 100%) or (100%, 0%).

Stability is crucial in practical applications of Nash equilibria, since the mixed strategy of each player is not perfectly known, but has to be inferred from statistical distribution of their actions in the game. In this case unstable equilibria are very unlikely to arise in practice, since any minute change in the proportions of each strategy seen will lead to a change in strategy and the breakdown of the equilibrium.

Finally in the eighties, building with great depth on such ideas Mertens-stable equilibria were introduced as a solution concept. Mertens stable equilibria satisfy both forward induction and backward induction. In a game theory context stable equilibria now usually refer to Mertens stable equilibria.^{[citation needed]}

Occurrence

If a game has a unique Nash equilibrium and is played among players under certain conditions, then the NE strategy set will be adopted. Sufficient conditions to guarantee that the Nash equilibrium is played are:

1. The players all will do their utmost to maximize their expected payoff as described by the game.
2. The players are flawless in execution.
3. The players have sufficient intelligence to deduce the solution.
4. The players know the planned equilibrium strategy of all of the other players.
5. The players believe that a deviation in their own strategy will not cause deviations by any other players.
6. There is common knowledge that all players meet these conditions, including this one. So, not only must each player know the other players meet the conditions, but also they must know that they all know that they meet them, and know that they know that they know that they meet them, and so on.

Where the conditions are not met

Examples of game theory problems in which these conditions are not met:

1. The first condition is not met if the game does not correctly describe the quantities a player wishes to maximize. In this case there is no particular reason for that player to adopt an equilibrium strategy. For instance, the prisoner's dilemma is not a dilemma if either player is happy to be jailed indefinitely.
2. Intentional or accidental imperfection in execution. For example, a computer capable of flawless logical play facing a second flawless computer will result in equilibrium. Introduction of imperfection will lead to its disruption either through loss to the player who makes the mistake, or through negation of the common knowledge criterion leading to possible victory for the player. (An example would be a player suddenly putting the car into reverse in the game of chicken, ensuring a no-loss no-win scenario).
3. In many cases, the third condition is not met because, even though the equilibrium must exist, it is unknown due to the complexity of the game, for instance in Chinese chess. Or, if known, it may not be known to all players, as when playing tic-tac-toe with a small child who desperately wants to win (meeting the other criteria).
4. The criterion of common knowledge may not be met even if all players do, in fact, meet all the other criteria. Players wrongly distrusting each other's rationality may adopt counter-strategies to expected irrational play on their opponents’ behalf. This is a major consideration in "chicken" or an arms race, for example.

Where the conditions are met

In his Ph.D. dissertation, John Nash proposed two interpretations of his equilibrium concept, with the objective of showing how equilibrium points can be connected with observable phenomenon.

(...) One interpretation is rationalistic: if we assume that players are rational, know the full structure of the game, the game is played just once, and there is just one Nash equilibrium, then players will play according to that equilibrium.

This idea was formalized by R. Aumann and A. Brandenburger, 1995, Epistemic Conditions for Nash Equilibrium, Econometrica, 63, 1161-1180 who interpreted each player's mixed strategy as a conjecture about the behaviour of other players and have shown that if the game and the rationality of players is mutually known and these conjectures are commonly known, then the conjectures must be a Nash equilibrium (a common prior assumption is needed for this result in general, but not in the case of two players. In this case, the conjectures need only be mutually known).

A second interpretation, that Nash referred to by the mass action interpretation, is less demanding on players:

[i]t is unnecessary to assume that the participants have full knowledge of the total structure of the game, or the ability and inclination to go through any complex reasoning processes. What is assumed is that there is a population of participants for each position in the game, which will be played throughout time by participants drawn at random from the different populations. If there is a stable average frequency with which each pure strategy is employed by the average member of the appropriate population, then this stable average frequency constitutes a mixed strategy Nash equilibrium.

For a formal result along these lines, see Kuhn, H. and et al., 1996, "The Work of John Nash in Game Theory", Journal of Economic Theory, 69, 153–185.

Due to the limited conditions in which NE can actually be observed, they are rarely treated as a guide to day-to-day behaviour, or observed in practice in human negotiations. However, as a theoretical concept in economics and evolutionary biology, the NE has explanatory power. The payoff in economics is utility (or sometimes money), and in evolutionary biology is gene transmission; both are the fundamental bottom line of survival. Researchers who apply games theory in these fields claim that strategies failing to maximize these for whatever reason will be competed out of the market or environment, which are ascribed the ability to test all strategies. This conclusion is drawn from the "stability" theory above. In these situations the assumption that the strategy observed is actually a NE has often been borne out by research.

NE and non-credible threats

Extensive and normal-form illustrations that show the difference between SPNE and other NE. The blue equilibrium is not subgame perfect because player two makes a non-credible threat at 2(2) to be unkind (U).

The Nash equilibrium is a superset of the subgame perfect Nash equilibrium. The subgame perfect equilibrium in addition to the Nash equilibrium requires that the strategy also is a Nash equilibrium in every subgame of that game. This eliminates all non-credible threats, that is, strategies that contain non-rational moves in order to make the counter-player change their strategy.

The image to the right shows a simple sequential game that illustrates the issue with subgame imperfect Nash equilibria. In this game player one chooses left(L) or right(R), which is followed by player two being called upon to be kind (K) or unkind (U) to player one, However, player two only stands to gain from being unkind if player one goes left. If player one goes right the rational player two would de facto be kind to her/him in that subgame. However, The non-credible threat of being unkind at 2(2) is still part of the blue (L, (U,U)) Nash equilibrium. Therefore, if rational behavior can be expected by both parties the subgame perfect Nash equilibrium may be a more meaningful solution concept when such dynamic inconsistencies arise.

Proof of existence

Proof using the Kakutani fixed-point theorem

Nash's original proof (in his thesis) used Brouwer's fixed-point theorem (e.g., see below for a variant). This section presents a simpler proof via the Kakutani fixed-point theorem, following Nash's 1950 paper (he credits David Gale with the observation that such a simplification is possible).

To prove the existence of a Nash equilibrium, let ${\displaystyle r_i({\sigma }_{-i})}$ be the best response of player i to the strategies of all other players. $${\displaystyle r_i({\sigma }_{-i})=\underset{{\sigma }_i}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}{u}_i({\sigma }_i,{\sigma }_{-i})}$$

Here, ${\displaystyle \sigma \in \mathrm{\Sigma }}$, where ${\displaystyle \mathrm{\Sigma }={\mathrm{\Sigma }}_i\times {\mathrm{\Sigma }}_{-i}}$, is a mixed-strategy profile in the set of all mixed strategies and ${\displaystyle u_i}$ is the payoff function for player i. Define a set-valued function ${\displaystyle r:\mathrm{\Sigma }\to 2^{\mathrm{\Sigma }}}$ such that ${\displaystyle r=r_i({\sigma }_{-i})\times r_{-i}({\sigma }_i)}$. The existence of a Nash equilibrium is equivalent to ${\displaystyle r}$ having a fixed point.

Kakutani's fixed point theorem guarantees the existence of a fixed point if the following four conditions are satisfied.

1. ${\displaystyle \mathrm{\Sigma }}$ is compact, convex, and nonempty.
2. ${\displaystyle r(\sigma )}$ is nonempty.
3. ${\displaystyle r(\sigma )}$ is upper hemicontinuous
4. ${\displaystyle r(\sigma )}$ is convex.

Condition 1. is satisfied from the fact that ${\displaystyle \mathrm{\Sigma }}$ is a simplex and thus compact. Convexity follows from players' ability to mix strategies. ${\displaystyle \mathrm{\Sigma }}$ is nonempty as long as players have strategies.

Condition 2. and 3. are satisfied by way of Berge's maximum theorem. Because ${\displaystyle u_i}$ is continuous and compact, ${\displaystyle r({\sigma }_i)}$ is non-empty and upper hemicontinuous.

Condition 4. is satisfied as a result of mixed strategies. Suppose ${\displaystyle {\sigma }_i,{\sigma }_i^{\prime }\in r({\sigma }_{-i})}$, then ${\displaystyle \lambda {\sigma }_i+(1-\lambda ){\sigma }_i^{\prime }\in r({\sigma }_{-i})}$. i.e. if two strategies maximize payoffs, then a mix between the two strategies will yield the same payoff.

Therefore, there exists a fixed point in ${\displaystyle r}$ and a Nash equilibrium.

When Nash made this point to John von Neumann in 1949, von Neumann famously dismissed it with the words, "That's trivial, you know. That's just a fixed-point theorem." (See Nasar, 1998, p. 94.)

Alternate proof using the Brouwer fixed-point theorem

We have a game ${\displaystyle G=(N,A,u)}$ where ${\displaystyle N}$ is the number of players and ${\displaystyle A=A_1\times \cdots \times A_N}$ is the action set for the players. All of the action sets ${\displaystyle A_i}$ are finite. Let ${\displaystyle \mathrm{\Delta }={\mathrm{\Delta }}_1\times \cdots \times {\mathrm{\Delta }}_N}$ denote the set of mixed strategies for the players. The finiteness of the ${\displaystyle A_i}$s ensures the compactness of ${\displaystyle \mathrm{\Delta }}$.

We can now define the gain functions. For a mixed strategy ${\displaystyle \sigma \in \mathrm{\Delta }}$, we let the gain for player ${\displaystyle i}$ on action ${\displaystyle a\in A_i}$ be $${\displaystyle {\text{Gain}}_i(\sigma ,a)=max\{0,u_i(a,{\sigma }_{-i})-u_i({\sigma }_i,{\sigma }_{-i})\}.}$$

The gain function represents the benefit a player gets by unilaterally changing their strategy. We now define ${\displaystyle g=(g_1,\dots ,g_N)}$ where $${\displaystyle g_i(\sigma )(a)={\sigma }_i(a)+{\text{Gain}}_i(\sigma ,a)}$$ for ${\displaystyle \sigma \in \mathrm{\Delta },a\in A_i}$. We see that $${\displaystyle \sum _{a\in A_i}{g}_i(\sigma )(a)=\sum _{a\in A_i}{\sigma }_i(a)+{\text{Gain}}_i(\sigma ,a)=1+\sum _{a\in A_i}{\text{Gain}}_i(\sigma ,a)>0.}$$

Next we define: $${\displaystyle \{\begin{array}{l}f=(f_1,\cdots ,f_N):\mathrm{\Delta }\to \mathrm{\Delta }\\ f_i(\sigma )(a)=\frac{g_i(\sigma )(a)}{\sum _{b\in A_i}{g}_i(\sigma )(b)}& a\in A_i\end{array}}$$

It is easy to see that each ${\displaystyle f_i}$ is a valid mixed strategy in ${\displaystyle {\mathrm{\Delta }}_i}$. It is also easy to check that each ${\displaystyle f_i}$ is a continuous function of ${\displaystyle \sigma }$, and hence ${\displaystyle f}$ is a continuous function. As the cross product of a finite number of compact convex sets, ${\displaystyle \mathrm{\Delta }}$ is also compact and convex. Applying the Brouwer fixed point theorem to ${\displaystyle f}$ and ${\displaystyle \mathrm{\Delta }}$ we conclude that ${\displaystyle f}$ has a fixed point in ${\displaystyle \mathrm{\Delta }}$, call it ${\displaystyle {\sigma }^{\ast }}$. We claim that ${\displaystyle {\sigma }^{\ast }}$ is a Nash equilibrium in ${\displaystyle G}$. For this purpose, it suffices to show that $${\displaystyle \mathrm{\forall }i\in \{1,\cdots ,N\},\mathrm{\forall }a\in A_i:{\text{Gain}}_i({\sigma }^{\ast },a)=0.}$$

This simply states that each player gains no benefit by unilaterally changing their strategy, which is exactly the necessary condition for a Nash equilibrium.

Now assume that the gains are not all zero. Therefore, ${\displaystyle \mathrm{\exists }i\in \{1,\cdots ,N\},}$ and ${\displaystyle a\in A_i}$ such that ${\displaystyle {\text{Gain}}_i({\sigma }^{\ast },a)>0}$. Then $${\displaystyle \sum _{a\in A_i}{g}_i({\sigma }^{\ast },a)=1+\sum _{a\in A_i}{\text{Gain}}_i({\sigma }^{\ast },a)>1.}$$

So let $${\displaystyle C=\sum _{a\in A_i}{g}_i({\sigma }^{\ast },a).}$$

Also we shall denote ${\displaystyle \text{Gain}(i,\cdot )}$ as the gain vector indexed by actions in ${\displaystyle A_i}$. Since ${\displaystyle {\sigma }^{\ast }}$ is the fixed point we have: $${\displaystyle \begin{array}{rl}{\sigma }^{\ast }=f({\sigma }^{\ast })& \Rightarrow {\sigma }_i^{\ast }=f_i({\sigma }^{\ast })\\ & \Rightarrow {\sigma }_i^{\ast }=\frac{g_i({\sigma }^{\ast })}{\sum _{a\in A_i}{g}_i({\sigma }^{\ast })(a)}\\ & \Rightarrow {\sigma }_i^{\ast }=\frac{1}{C}\left({\sigma }_i^{\ast }+{\text{Gain}}_i({\sigma }^{\ast },\cdot )\right)\\ & \Rightarrow C{\sigma }_i^{\ast }={\sigma }_i^{\ast }+{\text{Gain}}_i({\sigma }^{\ast },\cdot )\\ & \Rightarrow \left(C-1\right){\sigma }_i^{\ast }={\text{Gain}}_i({\sigma }^{\ast },\cdot )\\ & \Rightarrow {\sigma }_i^{\ast }=\left(\frac{1}{C-1}\right){\text{Gain}}_i({\sigma }^{\ast },\cdot ).\end{array}}$$

Since ${\displaystyle C>1}$ we have that ${\displaystyle {\sigma }_i^{\ast }}$ is some positive scaling of the vector ${\displaystyle {\text{Gain}}_i({\sigma }^{\ast },\cdot )}$. Now we claim that $${\displaystyle \mathrm{\forall }a\in A_i:{\sigma }_i^{\ast }(a)(u_i(a_i,{\sigma }_{-i}^{\ast })-u_i({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast }))={\sigma }_i^{\ast }(a){\text{Gain}}_i({\sigma }^{\ast },a)}$$

To see this, first if ${\displaystyle {\text{Gain}}_i({\sigma }^{\ast },a)>0}$ then this is true by definition of the gain function. Now assume that ${\displaystyle {\text{Gain}}_i({\sigma }^{\ast },a)=0}$. By our previous statements we have that $${\displaystyle {\sigma }_i^{\ast }(a)=\left(\frac{1}{C-1}\right){\text{Gain}}_i({\sigma }^{\ast },a)=0}$$

and so the left term is zero, giving us that the entire expression is ${\displaystyle 0}$ as needed.

So we finally have that $${\displaystyle \begin{array}{rl}0& =u_i({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast })-u_i({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast })\\ & =\left(\sum _{a\in A_i}{\sigma }_i^{\ast }(a)u_i(a_i,{\sigma }_{-i}^{\ast })\right)-u_i({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast })\\ & =\sum _{a\in A_i}{\sigma }_i^{\ast }(a)(u_i(a_i,{\sigma }_{-i}^{\ast })-u_i({\sigma }_i^{\ast },{\sigma }_{-i}^{\ast }))\\ & =\sum _{a\in A_i}{\sigma }_i^{\ast }(a){\text{Gain}}_i({\sigma }^{\ast },a)& & \text{ by the previous statements }\\ & =\sum _{a\in A_i}\left(C-1\right){\sigma }_i^{\ast }(a{)}^2>0\end{array}}$$

where the last inequality follows since ${\displaystyle {\sigma }_i^{\ast }}$ is a non-zero vector. But this is a clear contradiction, so all the gains must indeed be zero. Therefore, ${\displaystyle {\sigma }^{\ast }}$ is a Nash equilibrium for ${\displaystyle G}$ as needed.

Computing Nash equilibria

Main article: Nash equilibrium computation

If a player A has a dominant strategy ${\displaystyle s_A}$ then there exists a Nash equilibrium in which A plays ${\displaystyle s_A}$. In the case of two players A and B, there exists a Nash equilibrium in which A plays ${\displaystyle s_A}$ and B plays a best response to ${\displaystyle s_A}$. If ${\displaystyle s_A}$ is a strictly dominant strategy, A plays ${\displaystyle s_A}$ in all Nash equilibria. If both A and B have strictly dominant strategies, there exists a unique Nash equilibrium in which each plays their strictly dominant strategy.

In games with mixed-strategy Nash equilibria, the probability of a player choosing any particular (so pure) strategy can be computed by assigning a variable to each strategy that represents a fixed probability for choosing that strategy. In order for a player to be willing to randomize, their expected payoff for each (pure) strategy should be the same. In addition, the sum of the probabilities for each strategy of a particular player should be 1. This creates a system of equations from which the probabilities of choosing each strategy can be derived.

Examples

Matching pennies

Player A plays	Player B plays
	H	T
H	−1, +1	+1, −1
T	+1, −1	−1, +1

In the matching pennies game, player A loses a point to B if A and B play the same strategy and wins a point from B if they play different strategies. To compute the mixed-strategy Nash equilibrium, assign A the probability ${\displaystyle p}$ of playing H and ${\displaystyle (1-p)}$ of playing T, and assign B the probability ${\displaystyle q}$ of playing H and ${\displaystyle (1-q)}$ of playing T.

$${\displaystyle \begin{array}{rl}& \mathbb{E}[\text{payoff for A playing H}]=(-1)q+(+1)(1-q)=1-2q,\\ & \mathbb{E}[\text{payoff for A playing T}]=(+1)q+(-1)(1-q)=2q-1,\\ & \mathbb{E}[\text{payoff for A playing H}]=\mathbb{E}[\text{payoff for A playing T}]⟹1-2q=2q-1⟹q=\frac{1}{2}.\\ & \mathbb{E}[\text{payoff for B playing H}]=(+1)p+(-1)(1-p)=2p-1,\\ & \mathbb{E}[\text{payoff for B playing T}]=(-1)p+(+1)(1-p)=1-2p,\\ & \mathbb{E}[\text{payoff for B playing H}]=\mathbb{E}[\text{payoff for B playing T}]⟹2p-1=1-2p⟹p=\frac{1}{2}.\end{array}}$$

Thus, a mixed-strategy Nash equilibrium in this game is for each player to randomly choose H or T with ${\displaystyle p=\frac{1}{2}}$ and ${\displaystyle q=\frac{1}{2}}$.

Oddness of equilibrium points

Free money game

Player A votes	Player B votes
	Yes	No
Yes	1, 1	0, 0
No	0, 0	0, 0

In 1971, Robert Wilson came up with the "oddness theorem", which says that "almost all" finite games have a finite and odd number of Nash equilibria. In 1973, Harsanyi published an alternative proof of the result. "Almost all" here means that any game with an infinite or even number of equilibria is very special in the sense that if its payoffs were even slightly randomly perturbed, with probability one it would have an odd number of equilibria instead.

The prisoner's dilemma, for example, has one equilibrium, while the battle of the sexes has three—two pure and one mixed, and this remains true even if the payoffs change slightly. The free money game is an example of a "special" game with an even number of equilibria. In it, two players have to both vote "yes" rather than "no" to get a reward and the votes are simultaneous. There are two pure-strategy Nash equilibria, (yes, yes) and (no, no), and no mixed strategy equilibria, because the strategy "yes" weakly dominates "no". "Yes" is as good as "no" regardless of the other player's action, but if there is any chance the other player chooses "yes" then "yes" is the best reply. Under a small random perturbation of the payoffs, however, the probability that any two payoffs would remain tied, whether at 0 or some other number, is vanishingly small, and the game would have either one or three equilibria instead.

Phytochemical

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Phytochemical 

Red, blue, and purple colors of berries derive mainly from polyphenol phytochemicals called anthocyanins.

Cucurbita fruits, including squash and pumpkin, typically have high content of the phytochemical pigments called carotenoids.

Phytochemicals are naturally occurring chemicals present in or extracted from plants. Some phytochemicals are nutrients for the plant, while others are metabolites produced to enhance plant survivability and reproduction.

The fields of extracting phytochemicals for manufactured products or applying scientific methods to study phytochemical properties are called phytochemistry. An individual who uses phytochemicals in food chemistry manufacturing or research is a phytochemist.

Phytochemicals without a nutrient definition have no confirmed biological activities or proven health benefits when consumed in plant foods. Once phytochemicals in a food enter the digestion process, the fate of individual phytochemicals in the body is unknown due to extensive metabolism of the food in the gastrointestinal tract, producing phytochemical metabolites with different biological properties from those of the parent compound that may have been tested in vitro. Further, the bioavailability of many phytochemical metabolites appears to be low, as they are rapidly excreted from the body within minutes. Other than for dietary fiber, no non-nutrient phytochemicals have sufficient scientific evidence for providing a health benefit.

Some ingested phytochemicals may be toxic, and some may be used in cosmetics, drug discovery, or traditional medicine.

Etymology

Phytochemical derives by compounding the Ancient Greek word for plant (phytón, phyto) with chemical, as first used in English for plant chemistry and organic chemistry around 1850.

Definition

Phytochemicals are chemicals produced by plants through primary or secondary metabolism. They generally have biological activity in the plant host and play a role in plant growth or defense against competitors, pathogens, or predators. As components of plants, all individual phytochemicals make up the whole plant as it exists in nature.

Phytochemicals are generally regarded as research compounds rather than essential nutrients because proof of their possible health effects has not been established yet. Phytochemicals under research can be classified into major categories, such as carotenoids and polyphenols, which include phenolic acids, flavonoids, stilbenes or lignans. Flavonoids can be further divided into groups based on their similar chemical structure, such as anthocyanins, flavones, flavanones, isoflavones, and flavanols. Flavanols are further classified as catechins, epicatechins, and proanthocyanidins. In total, between 50,000 and 130,000 phytochemicals have been discovered.

Phytochemists study phytochemicals by first extracting and isolating compounds from the origin plant, followed by defining their structure or testing in laboratory model systems, such as in vitro studies or in vivo studies using laboratory animals. Challenges in that field include isolating specific compounds and determining their structures, which are often complex, and identifying what specific phytochemical is primarily responsible for any given biological activity.

Further, upon consuming phytochemicals in a food entering the digestion process, the fate of individual phytochemicals in the body is unknown due to extensive metabolism in the gastrointestinal tract, producing smaller phytochemical metabolites with different biological properties from those of the parent compound, and with low bioavailability and rapid excretion. Other than for dietary fiber, no non-nutrient phytochemical has sufficient scientific evidence in humans for an approved health claim.

History of uses

Berries of Atropa belladonna, also called deadly nightshade, containing the toxic phytochemicals, tropane alkaloids

Without specific knowledge of their cellular actions or mechanisms, phytochemicals can be toxic or used in traditional medicine. For example, salicin, having anti-inflammatory and pain-relieving properties, was originally extracted from the bark of the white willow tree and later synthetically produced to become the common, over-the-counter drug, aspirin. The tropane alkaloids of Atropa belladonna were used as poisons, and early humans made poisonous arrows from the plant. Other uses include perfumes, such as the sesquiterpene santolols, from sandalwood.

The English yew tree was long known to be extremely and immediately toxic to animals that grazed on its leaves or children who ate its berries; however, in 1971, paclitaxel was isolated from it, subsequently becoming a cancer drug.

Functions

The biological activities for most phytochemicals are unknown or poorly understood, in isolation or as part of foods. Phytochemicals with established roles in the body are classified as essential nutrients.

The phytochemical category includes compounds recognized as essential nutrients, which are naturally contained in plants and are required for normal physiological functions, so must be obtained from the diet in humans.

Some phytochemicals are known phytotoxins that are toxic to humans; for example aristolochic acid is carcinogenic at low doses. Some phytochemicals are antinutrients that interfere with the absorption of nutrients. Others, such as some polyphenols and flavonoids, may be pro-oxidants in high ingested amounts.

Non-digestible dietary fibers from plant foods, often considered as a phytochemical, are generally regarded as a nutrient group having approved health claims for reducing the risk of some types of cancer and coronary heart disease.

Phytochemical dietary supplements are neither recommended by health authorities for improving health nor are they approved by regulatory agencies for health claims on product labels.

Consumer and industry guidance

While health authorities encourage consumers to eat diets rich in fruit, vegetables, whole grains, legumes, and nuts to improve and maintain health, evidence that such effects result from specific, non-nutrient phytochemicals is limited or absent. For example, systematic reviews and/or meta-analyses indicate weak or no evidence for phytochemicals from plant food consumption having an effect on breast, lung, or bladder cancers. Further, in the United States, regulations exist to limit the language on product labels for how plant food consumption may affect cancers, excluding mention of any phytochemical except for those with established health benefits against cancer, such as dietary fiber, vitamin A, and vitamin C.

Phytochemicals, such as polyphenols, have been specifically discouraged from food labeling in Europe and the United States because there is no evidence for a cause-and-effect relationship between dietary polyphenols and inhibition or prevention of any disease.

Among carotenoids such as the tomato phytochemical, lycopene, the US Food and Drug Administration found insufficient evidence for its effects on any of several cancer types, resulting in limited language for how products containing lycopene can be described on labels.

Effects of food processing

Phytochemicals in freshly harvested plant foods may be degraded by processing techniques, including cooking. The main cause of phytochemical loss from cooking is thermal decomposition.

A converse exists in the case of carotenoids, such as lycopene present in tomatoes, which may remain stable or increase in content from cooking due to liberation from cellular membranes in the cooked food. Food processing techniques like mechanical processing can also free carotenoids and other phytochemicals from the food matrix, increasing dietary intake.

In some cases, processing of food is necessary to remove phytotoxins or antinutrients; for example societies that use cassava as a staple have traditional practices that involve some processing (soaking, cooking, fermentation), which are necessary to avoid illness from cyanogenic glycosides present in unprocessed cassava.

Seppuku

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Seppuku

Staged seppuku with ritual attire and kaishakunin assistant, 1897

Seppuku (切腹, lit. 'cutting [the] belly'), also called harakiri (腹切り, lit. 'abdomen/belly cutting', a native Japanese kun reading), is a form of Japanese ritualistic suicide by disembowelment. It was originally reserved for samurai in their code of honor, but was also practiced by other Japanese people during the Shōwa era (particularly officers near the end of World War II) to restore honor for themselves or for their families.

The practice dates back as far as the Heian period (794 to 1185), when it was done by samurai who were about to fall into the hands of their enemies and likely be tortured. By the time of the Meiji era (1868 to 1912), it had taken on an association with honor, and had also become a capital punishment for samurai who had committed serious offenses, sometimes involving a ritual imitation of cutting oneself (with a wooden dirk). The ceremonial disembowelment, which is usually part of a more elaborate ritual and performed in front of spectators, consists of plunging a short blade, traditionally a tantō, into the belly and drawing the blade from left to right, slicing the belly open. If the cut is deep enough, it can sever the abdominal aorta, causing death by rapid exsanguination.

One of the earliest recorded cases of seppuku was that of Minamoto no Tametomo, who had fought in the Hōgen war and, after being defeated, was exiled to Ōshima. He decided to try to take over the island. Minamoto's enemies sent troops to suppress his rebellion, so facing defeat, he committed seppuku in 1177. The ritual of seppuku was more concretely established when, in the early years of the Genpei war, Minamoto no Yorimasa committed seppuku after composing a poem.

Sometimes a daimyō was called upon to perform seppuku as the basis of a peace agreement. This weakened the defeated clan so that resistance effectively ceased. Toyotomi Hideyoshi used an enemy's suicide in this way on several occasions, the most dramatic of which effectively ended a dynasty of daimyōs. When the Hōjō clan were defeated at Odawara in 1590, Hideyoshi insisted on the suicide of the retired daimyō Hōjō Ujimasa and the exile of his son Ujinao. With this act of suicide, the most powerful daimyō family in eastern Japan was completely defeated.

Etymology

Samurai about to perform seppuku

The term seppuku is derived from the two Sino-Japanese roots setsu 切 ("to cut", from Middle Chinese tset; compare Mandarin qiē and Cantonese chit) and fuku 腹 ("belly", from MC pjuwk; compare Mandarin fù and Cantonese fūk). It is also known as harakiri (腹切り, "cutting the stomach"; often misspelled or mispronounced "hiri-kiri" or "hari-kari" by American English speakers. Harakiri is written with the same kanji as seppuku, but in reverse order with an okurigana. In Japanese, the more formal seppuku, a Chinese on'yomi reading, is typically used in writing, while harakiri, a native kun'yomi reading, is used in speech. As Ross notes,

It is commonly pointed out that hara-kiri is a vulgarism, but this is a misunderstanding. Hara-kiri is a Japanese reading or Kun-yomi of the characters; as it became customary to prefer Chinese readings in official announcements, only the term seppuku was ever used in writing. So hara-kiri is a spoken term, but only to commoners and seppuku a written term, but spoken amongst higher classes for the same act.

While harakiri refers to the act of disemboweling oneself, seppuku refers to the ritual and usually would involve decapitation after the act as a sign of mercy.

The practice of performing seppuku at the death of one's master, known as oibara (追腹 or 追い腹, the kun'yomi or Japanese reading) or tsuifuku (追腹, the on'yomi or Chinese reading), follows a similar ritual.

The word jigai (自害) means "suicide" in Japanese. The modern word for suicide is jisatsu (自殺); related words include jiketsu (自決), jijin (自尽) and jijin (自刃). In some popular western texts, such as martial arts magazines, the term is associated with the suicide of samurai wives. The term was introduced into English by Lafcadio Hearn in his Japan: An Attempt at Interpretation, an understanding which has since been translated into Japanese. Joshua S. Mostow notes that Hearn misunderstood the term jigai to be the female equivalent of seppuku. Mostow's context is analysis of Giacomo Puccini's Madame Butterfly and the original Cio-Cio San story by John Luther Long. Though both Long's story and Puccini's opera predate Hearn's use of the term jigai, the term has been used in relation to western Japonisme, which is the influence of Japanese culture on the western arts.

Ritual

A tantō prepared for seppuku

The practice of seppuku was not standardized until the 17th century. In the 12th and 13th centuries, such as with the seppuku of Minamoto no Yorimasa, the practice of a kaishakunin had not yet emerged; thus, the rite was considered far more painful. The defining characteristic was plunging either the tachi (longsword), wakizashi (shortsword) or tantō (knife) into the gut and slicing the abdomen horizontally. In the absence of a kaishakunin, the samurai would then remove the blade and stab himself in the throat, or fall onto the blade from a standing position with it positioned against his heart.

During the Edo period (1600–1867), carrying out seppuku came to involve an elaborate, detailed ritual. This was usually performed in front of spectators if it was planned, as opposed to one performed on a battlefield. A samurai was bathed in cold water (to prevent excessive bleeding), dressed in a white kimono called the shiro-shōzoku (白装束), and served his favorite foods for a last meal. When he had finished, the knife and cloth were placed on a sanbo and given to the warrior. Dressed ceremonially, with his sword placed in front of him and sometimes seated on special clothes, the warrior would prepare for death by writing a death poem. He would probably consume a ceremonial drink of sake and would also give his attendant a cup meant for sake.

With his selected kaishakunin standing by, he would open his kimono, take up his tantō – held by the blade with a cloth wrapped around so that it would not cut his hand and cause him to lose his grip – and plunge it into his abdomen, making a left-to-right cut. The kaishakunin would then perform kaishaku, a cut in which the warrior was partially decapitated. The maneuver should be done in the manners of dakikubi (lit. 'embraced head'), in which a slight band of flesh is left attaching the head to the body so that the head can dangle in front as if embraced. Because of the precision necessary for such a maneuver, the kaishakunin was a skilled swordsman. The principal and the kaishakunin agreed in advance when the latter was to make his cut. Usually, dakikubi would occur as soon as the dagger was plunged into the abdomen.

Over time, the process became so highly ritualized that as soon as the samurai reached for his blade, the kaishakunin would strike. Eventually, even the blade became unnecessary and the samurai could reach for something symbolic like a fan, and this alone would trigger the killing stroke from his kaishakunin. A fan was likely used when the samurai was too old to use a blade or in situations where it was too dangerous to give him a weapon.

This elaborate ritual evolved after seppuku had ceased being mainly a battlefield or wartime practice and became a para-judicial institution. The kaishakunin was usually, but not always, a friend. If a defeated warrior had fought honorably and well, an opponent who wanted to salute his bravery would volunteer to act as his kaishakunin.

In the Hagakure, Yamamoto Tsunetomo wrote:

From ages past it has been considered an ill-omen by samurai to be requested as kaishaku. The reason for this is that one gains no fame even if the job is well done. Further, if one should blunder, it becomes a lifetime disgrace. In the practice of past times, there were instances when the head flew off. It was said that it was best to cut leaving a little skin remaining so that it did not fly off in the direction of the verifying officials.

A specialized form of seppuku in feudal times was known as kanshi (諫死; lit. 'remonstration death or death of understanding'), in which a retainer would commit suicide in protest of a lord's decision. The retainer would make one deep, horizontal cut into his abdomen, then quickly bandage the wound. After this, the person would then appear before his lord, give a speech in which he announced the protest of the lord's action, then reveal his mortal wound. This is not to be confused with funshi (憤死; lit. 'indignation death'), which is any suicide made to protest or state dissatisfaction.

Some samurai chose to perform a considerably more taxing form of seppuku known as jūmonji giri (十文字切り; lit. 'cross-shaped cut'), in which there is no kaishakunin to put a quick end to the samurai's suffering. It involves a second and more painful vertical cut on the belly. A samurai performing jūmonji giri was expected to bear his suffering quietly until he bled to death, dying with his hands over his face.

Female ritual suicide

Female ritual suicide (incorrectly referred to in some English sources as jigai) was practiced by the wives of samurai who had performed seppuku or brought dishonour.

Some women belonging to samurai families died by suicide by cutting the arteries of the neck with one stroke, using a knife such as a tantō or kaiken. The main purpose was to achieve a quick and certain death in order to avoid capture or rape. Before dying, a woman would often tie her knees together so her body would be found in a "dignified" pose, despite the convulsions of death. Invading armies would often enter homes to find the lady of the house seated alone, facing away from the door. On approaching her, they would find that she had ended her life long before they reached her.

The wife of Onodera Junai, one of the Forty-seven Ronin, prepares for her suicide; note the legs tied together, a feature of female seppuku to ensure a decent posture in death

History

Stephen R. Turnbull provides extensive evidence for the practice of female ritual suicide, notably of samurai wives, in pre-modern Japan. One of the largest mass suicides was the 25 April 1185 final defeat of Taira no Tomomori. The wife of Onodera Junai, one of the Forty-seven Ronin, is a notable example of a wife following seppuku of a samurai husband. A large number of "honour suicides" marked the defeat of the Aizu clan in the Boshin War of 1869, leading into the Meiji era. For example, in the family of Saigō Tanomo, who survived, a total of twenty-two female honor suicides are recorded among one extended family.

Religious and social context

Voluntary death by drowning was a common form of ritual or honor suicide. The religious context of thirty-three Jōdo Shinshū adherents at the funeral of Abbot Jitsunyo in 1525 was faith in Amida Buddha and belief in rebirth in his Pure Land, but male seppuku did not have a specifically religious context. By way of contrast, the religious beliefs of Hosokawa Gracia, the Christian wife of daimyō Hosokawa Tadaoki, prevented her from committing suicide.

As capital punishment

While voluntary seppuku is the best known form, in practice, the most common form of seppuku was obligatory seppuku, used as a form of capital punishment for disgraced samurai, especially for those who committed a serious offense such as rape, robbery, corruption, unprovoked murder, or treason. The samurai were generally told of their offense in full and given a set time for them to commit seppuku, usually before sunset on a given day. On occasion, if the sentenced individuals were uncooperative, seppuku could be carried out by an executioner, or more often, the actual execution was carried out solely by decapitation while retaining only the trappings of seppuku; even the tantō laid out in front of the uncooperative offender could be replaced with a fan (to prevent uncooperative offenders from using the tantō as a weapon against the observers or the executioner). This form of involuntary seppuku was considered shameful and undignified. Unlike voluntary seppuku, seppuku carried out as capital punishment by executioners did not necessarily absolve or pardon the offender's family of the crime. Depending on the severity of the crime, all or part of the property of the condemned could be confiscated, and the family would be punished by being stripped of rank, sold into long-term servitude, or executed.

Seppuku was considered the most honorable capital punishment apportioned to samurai. Zanshu (斬首) and sarashikubi (晒し首), decapitation followed by a display of the head, was considered harsher and was reserved for samurai who committed greater crimes. The harshest punishments, usually involving death by torturous methods like kamayude (釜茹で) (death by boiling), were reserved for commoner offenders.

Forced seppuku came to be known as "conferred death" over time as it was used for punishment of criminal samurai.

Recorded events

Ōishi Yoshio was sentenced to commit seppuku in 1703.

On February 15, 1868, eleven French sailors of the Dupleix entered the town of Sakai without official permission. Their presence caused panic among the residents. Security forces were dispatched to turn the sailors back to their ship, but a fight broke out and the sailors were shot dead. Upon the protest of the French representative, financial compensation was paid, and those responsible were sentenced to death. Captain Abel-Nicolas Bergasse du Petit-Thouars was present to observe the execution. As each samurai committed ritual disembowelment, the violent act shocked the captain, and he requested a pardon, as a result of which nine of the samurai were spared. This incident was dramatized in a famous short story, "Sakai Jiken", by Mori Ōgai.

In the 1860s, the British Ambassador to Japan, Bertram Freeman-Mitford (Lord Redesdale), lived within sight of Sengaku-ji where the Forty-seven Ronin are buried. In his book Tales of Old Japan, he describes a man who had come to the graves to kill himself:

I will add one anecdote to show the sanctity which is attached to the graves of the Forty-seven. In the month of September 1868, a certain man came to pray before the grave of Oishi Chikara. Having finished his prayers, he deliberately performed hara-kiri, and, the belly wound not being mortal, dispatched himself by cutting his throat. Upon his person were found papers setting forth that, being a Ronin and without means of earning a living, he had petitioned to be allowed to enter the clan of the Prince of Choshiu, which he looked upon as the noblest clan in the realm; his petition having been refused, nothing remained for him but to die, for to be a Ronin was hateful to him, and he would serve no other master than the Prince of Choshiu: what more fitting place could he find in which to put an end to his life than the graveyard of these Braves? This happened at about two hundred yards' distance from my house, and when I saw the spot an hour or two later, the ground was all bespattered with blood, and disturbed by the death-struggles of the man.

Mitford also describes his friend's eyewitness account of a seppuku:

Illustration titled Harakiri: Condemnation of a nobleman to suicide; drawing by L. Crépon adapted from a Japanese painting, 1867

There are many stories on record of extraordinary heroism being displayed in the harakiri. The case of a young fellow, only twenty years old, of the Choshiu clan, which was told me the other day by an eye-witness, deserves mention as a marvellous instance of determination. Not content with giving himself the one necessary cut, he slashed himself thrice horizontally and twice vertically. Then he stabbed himself in the throat until the dirk protruded on the other side, with its sharp edge to the front; setting his teeth in one supreme effort, he drove the knife forward with both hands through his throat, and fell dead.

During the Meiji Restoration, the Tokugawa shogun's aide performed seppuku:

One more story and I have done. During the revolution, when the Taikun (Supreme Commander), beaten on every side, fled ignominiously to Yedo, he is said to have determined to fight no more, but to yield everything. A member of his second council went to him and said, "Sir, the only way for you now to retrieve the honor of the family of Tokugawa is to disembowel yourself; and to prove to you that I am sincere and disinterested in what I say, I am here ready to disembowel myself with you." The Taikun flew into a great rage, saying that he would listen to no such nonsense, and left the room. His faithful retainer, to prove his honesty, retired to another part of the castle, and solemnly performed the harakiri.

In his book Tales of Old Japan, Mitford describes witnessing a hara-kiri:

As a corollary to the above elaborate statement of the ceremonies proper to be observed at the harakiri, I may here describe an instance of such an execution which I was sent officially to witness. The condemned man was Taki Zenzaburo, an officer of the Prince of Bizen, who gave the order to fire upon the foreign settlement at Hyōgo in the month of February 1868, – an attack to which I have alluded in the preamble to the story of the Eta Maiden and the Hatamoto. Up to that time no foreigner had witnessed such an execution, which was rather looked upon as a traveler's fable.

The ceremony, which was ordered by the Mikado (Emperor) himself, took place at 10:30 at night in the temple of Seifukuji, the headquarters of the Satsuma troops at Hiogo. A witness was sent from each of the foreign legations. We were seven foreigners in all. After another profound obeisance, Taki Zenzaburo, in a voice which betrayed just so much emotion and hesitation as might be expected from a man who is making a painful confession, but with no sign of either in his face or manner, spoke as follows:

I, and I alone, unwarrantably gave the order to fire on the foreigners at Kobe, and again as they tried to escape. For this crime I disembowel myself, and I beg you who are present to do me the honour of witnessing the act.

Bowing once more, the speaker allowed his upper garments to slip down to his girdle, and remained naked to the waist. Carefully, according to custom, he tucked his sleeves under his knees to prevent himself from falling backwards; for a noble Japanese gentleman should die falling forwards. Deliberately, with a steady hand, he took the dirk that lay before him; he looked at it wistfully, almost affectionately; for a moment he seemed to collect his thoughts for the last time, and then stabbing himself deeply below the waist on the left-hand side, he drew the dirk slowly across to the right side, and, turning it in the wound, gave a slight cut upwards. During this sickeningly painful operation he never moved a muscle of his face. When he drew out the dirk, he leaned forward and stretched out his neck; an expression of pain for the first time crossed his face, but he uttered no sound. At that moment the kaishaku, who, still crouching by his side, had been keenly watching his every movement, sprang to his feet, poised his sword for a second in the air; there was a flash, a heavy, ugly thud, a crashing fall; with one blow the head had been severed from the body.

A dead silence followed, broken only by the hideous noise of the blood throbbing out of the inert heap before us, which but a moment before had been a brave and chivalrous man. It was horrible.

The kaishaku made a low bow, wiped his sword with a piece of rice paper which he had ready for the purpose, and retired from the raised floor; and the stained dirk was solemnly borne away, a bloody proof of the execution. The two representatives of the Mikado then left their places, and, crossing over to where the foreign witnesses sat, called us to witness that the sentence of death upon Taki Zenzaburo had been faithfully carried out. The ceremony being at an end, we left the temple. The ceremony, to which the place and the hour gave an additional solemnity, was characterized throughout by that extreme dignity and punctiliousness which are the distinctive marks of the proceedings of Japanese gentlemen of rank; and it is important to note this fact, because it carries with it the conviction that the dead man was indeed the officer who had committed the crime, and no substitute. While profoundly impressed by the terrible scene it was impossible at the same time not to be filled with admiration of the firm and manly bearing of the sufferer, and of the nerve with which the kaishaku performed his last duty to his master.

In modern Japan

Seppuku as judicial punishment was abolished in 1873, shortly after the Meiji Restoration, but voluntary seppuku did not completely die out. It persisted still among the armed forces, with a famous example being the seppuku of General Nogi Maresuke and his wife on the death of Emperor Meiji in 1912. It also occurred during World War II. The practice had been widely praised in army propaganda, which featured a soldier captured by the Chinese in the Shanghai Incident (1932) who returned to the site of his capture to perform seppuku. Many high-ranking military officials of Imperial Japan committed seppuku toward the latter half of World War II in 1944 and 1945, as the tide of the war turned against the Japanese, and it became clear that a Japanese victory of the war was not achievable.

In 1970, ultranationalist author Yukio Mishima and one of his followers performed public seppuku at the Japan Self-Defense Forces headquarters following an unsuccessful attempt to incite the armed forces to stage a coup d'état. Mishima performed seppuku in the office of General Kanetoshi Mashita. His kaishakunin, a 25-year-old man named Masakatsu Morita, tried three times to ritually behead Mishima but failed, and his head was finally severed by Hiroyasu Koga, a former kendo champion. Morita then attempted to perform seppuku himself, but when his own cuts were too shallow to be fatal, he gave the signal and was beheaded by Koga.

Notable cases

List of notable seppuku cases in chronological order.

• Minamoto no Tametomo (1170)
• Minamoto no Yorimasa (1180)
• Minamoto no Yoshitsune (1189)
• Hōjō Takatoki (1333)
• Ashikaga Mochiuji (1439)
• Azai Nagamasa (1573)
• Oda Nobunaga (1582)
• Takeda Katsuyori (1582)
• Shibata Katsuie (1583)
• Sassa Narimasa (1588)
• Hōjō Ujimasa (1590)
• Sen no Rikyū (1591)
• Toyotomi Hidetsugu (1595)
• Torii Mototada (1600)
• Tokugawa Tadanaga (1634)
• Forty-six of the Forty-seven rōnin (1703)
• Watanabe Kazan (1841)
• Tanaka Shinbei (1863)
• Takechi Hanpeita (1865)
• Yamanami Keisuke (1865)
• Byakkotai (group of samurai youths) (1868)
• Saigō Takamori (1877)

• Nogi Maresuke and Nogi Shizuko (1912)
• Chujiro Hayashi (1940)
• Seigō Nakano (1943)
• Yoshitsugu Saitō (1944)
• Hideyoshi Obata (1944)
• Kunio Nakagawa (1944)
• Mitsuru Ushijima (1945)
• Isamu Chō (1945)
• Korechika Anami (1945)
• Takijirō Ōnishi (1945)
• Chikahiko Koizumi (1945)
• Yukio Mishima (1970)
• Masakatsu Morita (1970)
• Isao Inokuma (2001)

In popular culture

In Joseph Keppler's cartoon published in Frank Leslie's Illustrated Newspaper on March 8, 1873, Uncle Sam is shown directing U.S. Senators implicated in the Crédit Mobilier Scandal to commit "Hari-Kari", clearly showing that by that time the general American public was already familiar with the Japanese ritual and its social implications.

The story of the forty-seven rōnin (Chūshingura), who commit mass seppuku after avenging their lord, has inspired numerous works of Japanese art including bunraku puppet plays, kabuki plays and at least six film adaptations, as well as the Hollywood movie 47 Ronin.

The expected honor suicide of the samurai wife is frequently referenced in Japanese literature and film, such as in Taiko by Eiji Yoshikawa, Humanity and Paper Balloons, and Rashomon.

In Puccini's 1904 opera Madame Butterfly, wronged child-bride Cio-Cio-san commits seppuku in the final moments of the opera, after hearing that the father of her child—although he has finally returned to Japan, much to her initial delight—had in the meantime married an American lady and has come to take her child away from her.

Seppuku is referenced and described multiple times in the 1975 James Clavell novel, Shōgun; its subsequent 1980 miniseries Shōgun brought the term and the concept to mainstream Western attention. The 2024 adaptation also follows suit in this vein, in greater graphic detail.

Collective behavior

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Collective_behavior

Collective behavior constitutes social processes and events which do not reflect existing social structure (laws, conventions, and institutions), but which emerge in a "spontaneous" way. More broadly, it can include the behavior of cells, social animals like birds and fish, and insects including ants.

Collective behavior takes many forms but generally violates societal norms. Collective behavior can be destructive, as with riots or mob violence, silly, as with fads, or anywhere in between. Collective behavior is always driven by group dynamics, encouraging people to engage in acts they might consider unthinkable under typical social circumstances.

Defining the field

Further information: Collective animal behavior

The concept was introduced by Franklin Henry Giddings and employed later by Robert Park and Ernest Burgess, Herbert Blumer, Ralph H. Turner and Lewis Killian, and Neil Smelser.

Turner and Killian were the first sociologists to back their theoretical propositions with visual evidence in the form of photographs and motion pictures of collective behavior in action. Prior to that sociologists relied heavily upon eyewitness accounts, which turned out to be far less reliable than one would hope.

Turner and Killian's approach is based largely upon the arguments of Blumer, who argued that social "forces" are not really forces. The actor is active: He creates an interpretation of the acts of others, and acts on the basis of this interpretation.

Examples

Here are some instances of collective behavior: the Los Angeles riot of 1992, the hula-hoop fad of 1958, the stock market crashes of 1929, and the "phantom gasser" episodes in Virginia in 1933–34 and Mattoon, IL in 1944. The claim that such diverse episodes all belong to a single field of inquiry is a theoretical assertion, and not all sociologists would agree with it. But Blumer and Neil Smelser did agree, as did others, indicating that the formulation has satisfied some leading sociological thinkers.

Four forms

Although there are several other schema that may be used to classify forms of collective behavior the following four categories from Blumer are generally considered useful by most sociologists.

The crowd

Scholars differ about what classes of social events fall under the rubric of collective behavior. In fact, the only class of events which all authors include is crowds. Clark McPhail is one of those who treats crowds and collective behavior as synonyms. Although some consider McPhail's work overly simplistic, his important contribution is to have gone beyond the speculations of others to carry out pioneering empirical studies of crowds. He finds them to form an elaborate set of types.

The classic treatment of crowds is Gustave LeBon, The Crowd: A Study of the Popular Mind, in which the author interpreted the crowds of the French Revolution as irrational reversions to animal emotion, and inferred from this that such reversion is characteristic of crowds in general. LeBon believed that crowds somehow induced people to lose their ability to think rationally and to somehow recover this ability once they had left the crowd. He speculated, but could not explain how this might occur. Freud expressed a similar view in Group Psychology and the Analysis of the Ego. Such authors have thought that their ideas were confirmed by various kinds of crowds, one of these being the economic bubble. In Holland, during the tulip mania (1637), the prices of tulip bulbs rose to astronomical heights. An array of such crazes and other historical oddities is narrated in Charles MacKay's Extraordinary Popular Delusions and the Madness of Crowds.

At the University of Chicago, Robert Park and Herbert Blumer agreed with the speculations of LeBon and other that crowds are indeed emotional. But to them a crowd is capable of any emotion, not only the negative ones of anger and fear.

A number of authors modify the common-sense notion of the crowd to include episodes during which the participants are not assembled in one place but are dispersed over a large area. Turner and Killian refer to such episodes as diffuse crowds, examples being Billy Graham's revivals, panics about sexual perils, witch hunts and Red scares. Their expanded definition of the crowd is justified if propositions which hold true among compact crowds do so for diffuse crowds as well.

Some psychologists have claimed that there are three fundamental human emotions: fear, joy, and anger. Neil Smelser, John Lofland, and others have proposed three corresponding forms of the crowd: the panic (an expression of fear), the craze (an expression of joy), and the hostile outburst (an expression of anger). Each of the three emotions can characterize either a compact or a diffuse crowd, the result being a scheme of six types of crowds. Lofland has offered the most explicit discussion of these types.

The public

Boom distinguishes the crowd, which expresses a common emotion, from a public, which discusses a single issue. Thus, a public is not equivalent to all of the members of a society. Obviously, this is not the usual use of the word, "public." To Park and Blumer, there are as many publics as there are issues. A public comes into being when discussion of an issue begins, and ceases to be when it reaches a decision on it.

The mass

To the crowd and the public Blumer adds a third form of collective behavior, the mass. It differs from both the crowd and the public in that it is defined not by a form of interaction but by the efforts of those who use the mass media to address an audience. The first mass medium was printing.

The social movement

Main article: Social movement

We change intellectual gears when we confront Blumer's final form of collective behavior, the social movement. He identifies several types of these, among which are active social movements such as the French Revolution and expressive ones such as Alcoholics Anonymous. An active movement tries to change society; an expressive one tries to change its own members.

The social movement is the form of collective behavior which satisfies least well the first definition of it which was offered at the beginning of this article. These episodes are less fluid than the other forms, and do not change as often as other forms do. Furthermore, as can be seen in the history of the labor movement and many religious sects, a social movement may begin as collective behavior but over time become firmly established as a social institution.

For this reason, social movements are often considered a separate field of sociology. The books and articles about them are far more numerous than the sum of studies of all the other forms of collective behavior put together. Social movements are considered in many Wikipedia articles, and an article on the field of social movements as a whole would be much longer than this essay.

The study of collective behavior spun its wheels for many years, but began to make progress with the appearance of Turner and Killian's "Collective Behavior" and Smelser's Theory of Collective Behavior. Both books pushed the topic of collective behavior back into the consciousness of American sociologists and both theories contributed immensely to our understanding of collective behavior. Social disturbances in the U. S. and elsewhere in the late '60s and early '70s inspired another surge of interest in crowds and social movements. These studies presented a number of challenges to the armchair sociology of earlier students of collective behavior.

Theories developed to explain collective behavior

Social scientists have developed various theories to explain crowd behavior.

1. Contagion theory – according to the contagion theory as formulated by French thinker Gustave Le Bon (1841-1931), crowds exert a hypnotic influence over their members. Shielded by anonymity, large numbers of people abandon personal responsibility and surrender to the contagious emotions of the crowd. A crowd thus assumes a life of its own, stirring up emotions and driving people toward irrational, even violent action. Le Bon's theory, although one of the earliest explanations of crowd behavior, is still accepted by many people outside of sociology.  However, critics argue that the "collective mind" has not been documented by systematic studies. Furthermore, although collective behavior may involve strong emotions, such feelings are not necessarily irrational. Turner and Killian argue convincingly that the "contagion" never actually occurs and that participants in collective behavior do not lose their ability to think rationally.
2. Convergence theory – whereas the contagion theory suggests that crowds cause people to act in a certain way, convergence theory states that people who want to act in a certain way come together to form crowds. Developed by Floyd Allport (1890-1979) and later expanded upon by Neal Miller (1909-2002) and John Dollard (1900-1980) as "Learning Theory", the central argument of all convergence theories is that collective behavior reveals the otherwise hidden tendencies of the individuals who take part in the episode. The theory asserts that people with similar attributes find other like-minded persons with whom they can release these underlying tendencies. People sometimes do things in a crowd that they would not have the courage to do alone - because crowds can diffuse responsibility - but the behavior itself is claimed to originate within the individuals. Crowds, in addition, can intensify a sentiment simply by creating a critical mass of like-minded people.
3. Emergent-norm theory – according to sociologists Ralph Turner (1919-2014) and Lewis Killian, crowds begin as collectivities composed of people with mixed interests and motives. Especially in the case of less-stable crowds — expressive, acting and protest crowds — norms may be vague and changing, as when one person decides to break the glass windows of a store and others join in and begin looting merchandise. When people find themselves in a situation that is vague, ambiguous, or confusing, new norms "emerge" on the spot and people follow those emergent norms, which may be at odds with normal social behavior. Turner and Killian further argue that there are several different categories of participants, all of whom follow different patterns of behavior due to their differing motivations.
4. Value-added theory – Professor Neil Smelser (1930-2017) argues that collective behavior is actually a sort of release-valve for built-up tension ("strain") within a social system, community, or group. If the proper determinants are present then collective behavior becomes inevitable. Conversely, if any of the key determinants are not present no collective behavior will occur unless and until the missing determinants fall into place. These are primarily social, although physical factors such as location and weather may also contribute to or hinder the development of collective behavior.
5. Complex Adaptive Systems theory – Dutch scholar Jaap van Ginneken (1943- ) claims that contagion, convergence and emergent norms are just instances of the synergy, emergence and autopoiesis or self-creation of patterns and new entities typical for the newly discovered meta-category of complex adaptive systems. This also helps explain the key role of salient details and path-dependence in rapid shifts.
6. Shared intentionality theory – Cognitive psychologist Professor Michael Tomasello (1950- ) developed the psychological construct of shared intentionality through his insights into cognition evolution and, specifically, the knowledge development about the contribution of shared intentionality to the formation of a social reality. Shared intentionality provides unaware processes in mother-child dyads during social learning when young organisms can only manifest simple reflexes. It increases the cognitive performance of children indwelling with mothers who know the correct answer. This interaction proceeds without communication within the dyad using sensory cues. Professor Igor Val Danilov argues that this performance succeeds due to sharing an essential stimulus during a single cognitive task in the shared ecological context. Furthermore, research shows that shared intentionality can appear even in groups of more mature organisms due to their physiological synchrony and group dynamics. Therefore, this interaction can provide subliminal compliance of the participants to the group decisions, encouraging people to engage in acts they might consider unthinkable under typical social circumstances. The hypothesis of neurobiological processes occurring during shared intentionality explains how organisms can share relevant sensory stimuli without communication within the group using sensory cues.