Search This Blog

Thursday, March 19, 2015

Pauli exclusion principle


From Wikipedia, the free encyclopedia


Wolfgang Pauli

The Pauli exclusion principle is the quantum mechanical principle that says that two identical fermions (particles with half-integer spin) cannot occupy the same quantum state simultaneously. In the case of electrons, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers (n, ℓ, mℓ and ms). For two electrons residing in the same orbital, n, ℓ, and mℓ are the same, so ms must be different and the electrons have opposite spins. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925.

A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles. This means that the wave function changes its sign if the space and spin co-ordinates of any two particles are interchanged.

Integer spin particles, bosons, are not subject to the Pauli exclusion principle: any number of identical bosons can occupy the same quantum state, as with, for instance, photons produced by a laser and Bose–Einstein condensate.

Overview

The Pauli exclusion principle governs the behavior of all fermions (particles with "half-integer spin"), while bosons (particles with "integer spin") are not subject to it. Fermions include elementary particles such as quarks (the constituent particles of protons and neutrons), electrons and neutrinos. In addition, protons and neutrons (subatomic particles composed from three quarks) and some atoms are fermions, and are therefore subject to the Pauli exclusion principle as well. Atoms can have different overall "spin", which determines whether they are fermions or bosons — for example helium-3 has spin 1/2 and is therefore a fermion, in contrast to helium-4 which has spin 0 and is a boson.[1]:123–125 As such, the Pauli exclusion principle underpins many properties of everyday matter, from its large-scale stability, to the chemical behavior of atoms.

"Half-integer spin" means that the intrinsic angular momentum value of fermions is 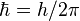\hbar = h/2\pi (reduced Planck's constant) times a half-integer (1/2, 3/2, 5/2, etc.). In the theory of quantum mechanics fermions are described by antisymmetric states. In contrast, particles with integer spin (called bosons) have symmetric wave functions; unlike fermions they may share the same quantum states. Bosons include the photon, the Cooper pairs which are responsible for superconductivity, and the W and Z bosons. (Fermions take their name from the Fermi–Dirac statistical distribution that they obey, and bosons from their Bose–Einstein distribution).

History

In the early 20th century it became evident that atoms and molecules with even numbers of electrons are more chemically stable than those with odd numbers of electrons. In the 1916 article "The Atom and the Molecule" by Gilbert N. Lewis, for example, the third of his six postulates of chemical behavior states that the atom tends to hold an even number of electrons in the shell and especially to hold eight electrons which are normally arranged symmetrically at the eight corners of a cube (see: cubical atom).[2] In 1919 chemist Irving Langmuir suggested that the periodic table could be explained if the electrons in an atom were connected or clustered in some manner.
Groups of electrons were thought to occupy a set of electron shells around the nucleus.[3] In 1922, Niels Bohr updated his model of the atom by assuming that certain numbers of electrons (for example 2, 8 and 18) corresponded to stable "closed shells".[4]:203

Pauli looked for an explanation for these numbers, which were at first only empirical. At the same time he was trying to explain experimental results of the Zeeman effect in atomic spectroscopy and in ferromagnetism. He found an essential clue in a 1924 paper by Edmund C. Stoner, which pointed out that for a given value of the principal quantum number (n), the number of energy levels of a single electron in the alkali metal spectra in an external magnetic field, where all degenerate energy levels are separated, is equal to the number of electrons in the closed shell of the noble gases for the same value of n. This led Pauli to realize that the complicated numbers of electrons in closed shells can be reduced to the simple rule of one electron per state, if the electron states are defined using four quantum numbers. For this purpose he introduced a new two-valued quantum number, identified by Samuel Goudsmit and George Uhlenbeck as electron spin.[5]

Connection to quantum state symmetry

The Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to requiring the wavefunction to be antisymmetric. An antisymmetric two-particle state is represented as a sum of states in which one particle is in state \scriptstyle |x \rangle and the other in state \scriptstyle |y\rangle:
|\psi\rangle = \sum_{x,y} A(x,y) |x,y\rangle,
and antisymmetry under exchange means that A(x,y) = −A(y,x). This implies A(x,y) = 0 when x=y, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two tensor.

Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component
A(x,y)=\langle \psi|x,y\rangle = \langle \psi | ( |x\rangle \otimes |y\rangle )
is necessarily antisymmetric. To prove it, consider the matrix element
\langle\psi| \Big((|x\rangle + |y\rangle)\otimes(|x\rangle + |y\rangle)\Big).
This is zero, because the two particles have zero probability to both be in the superposition state |x\rangle + |y\rangle. But this is equal to
\langle \psi |x,x\rangle + \langle \psi |x,y\rangle + \langle \psi |y,x\rangle + \langle \psi | y,y \rangle.
The first and last terms on the right side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:
\langle \psi|x,y\rangle + \langle\psi |y,x\rangle = 0,
or
A(x,y) = -A(y,x).

Pauli principle in advanced quantum theory

According to the spin-statistics theorem, particles with integer spin occupy symmetric quantum states, and particles with half-integer spin occupy antisymmetric states; furthermore, only integer or half-integer values of spin are allowed by the principles of quantum mechanics. In relativistic quantum field theory, the Pauli principle follows from applying a rotation operator in imaginary time to particles of half-integer spin.

In one dimension, bosons, as well as fermions, can obey the exclusion principle. A one-dimensional Bose gas with delta-function repulsive interactions of infinite strength is equivalent to a gas of free fermions. The reason for this is that, in one dimension, exchange of particles requires that they pass through each other; for infinitely strong repulsion this cannot happen. This model is described by a quantum nonlinear Schrödinger equation. In momentum space the exclusion principle is valid also for finite repulsion in a Bose gas with delta-function interactions,[6] as well as for interacting spins and Hubbard model in one dimension, and for other models solvable by Bethe ansatz. The ground state in models solvable by Bethe ansatz is a Fermi sphere.

Consequences

Atoms and the Pauli principle

The Pauli exclusion principle helps explain a wide variety of physical phenomena. One particularly important consequence of the principle is the elaborate electron shell structure of atoms and the way atoms share electrons, explaining the variety of chemical elements and their chemical combinations. An electrically neutral atom contains bound electrons equal in number to the protons in the nucleus. Electrons, being fermions, cannot occupy the same quantum state as other electrons, so electrons have to "stack" within an atom, i.e. have different spins while at the same electron orbital as described below.

An example is the neutral helium atom, which has two bound electrons, both of which can occupy the lowest-energy (1s) states by acquiring opposite spin; as spin is part of the quantum state of the electron, the two electrons are in different quantum states and do not violate the Pauli principle. However, the spin can take only two different values (eigenvalues). In a lithium atom, with three bound electrons, the third electron cannot reside in a 1s state, and must occupy one of the higher-energy 2s states instead. Similarly, successively larger elements must have shells of successively higher energy. The chemical properties of an element largely depend on the number of electrons in the outermost shell; atoms with different numbers of shells but the same number of electrons in the outermost shell have similar properties, which gives rise to the periodic table of the elements.[7]:214–218

Solid state properties and the Pauli principle

In conductors and semiconductors, there are very large numbers of molecular orbitals which effectively form a continuous band structure of energy levels. In strong conductors (metals) electrons are so degenerate that they cannot even contribute much to the thermal capacity of a metal.[8]:133–147 Many mechanical, electrical, magnetic, optical and chemical properties of solids are the direct consequence of Pauli exclusion.

Stability of matter

The stability of the electrons in an atom itself is unrelated to the exclusion principle, but is described by the quantum theory of the atom. The underlying idea is that close approach of an electron to the nucleus of the atom necessarily increases its kinetic energy, an application of the uncertainty principle of Heisenberg.[9] However, stability of large systems with many electrons and many nucleons is a different matter, and requires the Pauli exclusion principle.[10]

It has been shown that the Pauli exclusion principle is responsible for the fact that ordinary bulk matter is stable and occupies volume. This suggestion was first made in 1931 by Paul Ehrenfest, who pointed out that the electrons of each atom cannot all fall into the lowest-energy orbital and must occupy successively larger shells. Atoms therefore occupy a volume and cannot be squeezed too closely together.[11]

A more rigorous proof was provided in 1967 by Freeman Dyson and Andrew Lenard, who considered the balance of attractive (electron–nuclear) and repulsive (electron–electron and nuclear–nuclear) forces and showed that ordinary matter would collapse and occupy a much smaller volume without the Pauli principle.[12][13]

The consequence of the Pauli principle here is that electrons of the same spin are kept apart by a repulsive exchange interaction, which is a short-range effect, acting simultaneously with the long-range electrostatic or coulombic force. This effect is partly responsible for the everyday observation in the macroscopic world that two solid objects cannot be in the same place at the same time.

Astrophysics and the Pauli principle

Dyson and Lenard did not consider the extreme magnetic or gravitational forces which occur in some astronomical objects. In 1995 Elliott Lieb and coworkers showed that the Pauli principle still leads to stability in intense magnetic fields such as in neutron stars, although at a much higher density than in ordinary matter.[14] It is a consequence of general relativity that, in sufficiently intense gravitational fields, matter collapses to form a black hole.

Astronomy provides a spectacular demonstration of the effect of the Pauli principle, in the form of white dwarf and neutron stars. In both types of body, atomic structure is disrupted by large gravitational forces, leaving the constituents supported by "degeneracy pressure" alone. This exotic form of matter is known as degenerate matter. In white dwarfs atoms are held apart by electron degeneracy pressure. In neutron stars, subject to even stronger gravitational forces, electrons have merged with protons to form neutrons. Neutrons are capable of producing an even higher degeneracy pressure, albeit over a shorter range. This can stabilize neutron stars from further collapse, but at a smaller size and higher density than a white dwarf. Neutrons are the most "rigid" objects known; their Young modulus (or more accurately, bulk modulus) is 20 orders of magnitude larger than that of diamond. However, even this enormous rigidity can be overcome by the gravitational field of a massive star or by the pressure of a supernova, leading to the formation of a black hole.[15]:286–287

at

Degenerate matter


From Wikipedia, the free encyclopedia

Degenerate matter[1][2] in physics is a collection of free, non-interacting particles with a pressure and other physical characteristics determined by quantum mechanical effects. It is the analogue of an ideal gas in classical mechanics. The degenerate state of matter, in the sense of deviant from an ideal gas, arises at extraordinarily high density (in compact stars) or at extremely low temperatures in laboratories.[3][4] It occurs for matter particles such as electrons, neutrons, protons, and fermions in general and is referred to as electron-degenerate matter, neutron-degenerate matter, etc. In a mixture of particles, such as ions and electrons in white dwarfs or metals, the electrons may be degenerate, while the ions are not.

In a quantum mechanical description, free particles limited to a finite volume may take only a discrete set of energies, called quantum states. The Pauli exclusion principle prevents identical fermions from occupying the same quantum state. At lowest total energy (when the thermal energy of the particles is negligible), all the lowest energy quantum states are filled. This state is referred to as full degeneracy. The pressure (called degeneracy pressure or Fermi pressure) remains nonzero even near absolute zero temperature.[3][4] Adding particles or reducing the volume forces the particles into higher-energy quantum states. This requires a compression force, and is made manifest as a resisting pressure. The key feature is that this degeneracy pressure does not depend on the temperature and only on the density of the fermions. It keeps dense stars in equilibrium independent of the thermal structure of the star.

Degenerate matter is also called a Fermi gas or a degenerate gas. A degenerate state with velocities of the fermions close to the speed of light (particle energy larger than its rest mass energy) is called relativistic degenerate matter.

Degenerate matter was first described for a mixture of ions and electrons in 1926 by Ralph H. Fowler,[5] showing that at densities observed in white dwarfs the electrons (obeying Fermi–Dirac statistics, the term degenerate was not yet in use) have a pressure much higher than the partial pressure of the ions.

Concept

Imagine that a plasma is cooled and compressed repeatedly. Eventually, it will not be possible to compress the plasma any further, because the Pauli exclusion principle states that two fermions cannot share the same quantum state. When in this state, since there is no extra space for any particles, we can also say that a particle's location is extremely defined. Therefore, since (according to the Heisenberg uncertainty principle) ΔpΔx ≥ ħ/2 where Δp is the uncertainty in the particle's momentum and Δx is the uncertainty in position, then we must say that their momentum is extremely uncertain since the particles are located in a very confined space. Therefore, even though the plasma is cold, the particles must be moving very fast on average. This leads to the conclusion that in order to compress an object into a very small space, tremendous force is required to control its particles' momentum.

Unlike a classical ideal gas, whose pressure is proportional to its temperature (P = nkT/V, where P is pressure, V is the volume, n is the number of particles—typically atoms or molecules—k is Boltzmann's constant, and T is temperature), the pressure exerted by degenerate matter depends only weakly on its temperature. In particular, the pressure remains nonzero even at absolute zero temperature. At relatively low densities, the pressure of a fully degenerate gas is given by P = K(n/V)5/3, where K depends on the properties of the particles making up the gas. At very high densities, where most of the particles are forced into quantum states with relativistic energies, the pressure is given by P = K′(n/V)4/3, where K′ again depends on the properties of the particles making up the gas.[6]

All matter experiences both normal thermal pressure and degeneracy pressure, but in commonly encountered gases, thermal pressure dominates so much that degeneracy pressure can be ignored. Likewise, degenerate matter still has normal thermal pressure, but at extremely high densities the degeneracy pressure usually dominates.

Exotic examples of degenerate matter include neutronium, strange matter, metallic hydrogen and white dwarf matter. Degeneracy pressure contributes to the pressure of conventional solids, but these are not usually considered to be degenerate matter because a significant contribution to their pressure is provided by electrical repulsion of atomic nuclei and the screening of nuclei from each other by electrons. In metals it is useful to treat the conduction electrons alone as a degenerate, free electron gas while the majority of the electrons are regarded as occupying bound quantum states. This contrasts with degenerate matter that forms the body of a white dwarf, where all the electrons would be treated as occupying free particle momentum states.

Degenerate gases

Degenerate gases are gases composed of fermions that have a particular configuration that usually forms at high densities. Fermions are particles with half-integer spin. Their behavior is regulated by a set of quantum mechanical rules called the Fermi–Dirac statistics. One particular rule is the Pauli exclusion principle, which states that there can be only one fermion occupying each quantum state, which also applies to electrons that are not bound to a nucleus but merely confined to a fixed volume, such as in the deep interior of a star. Such particles as electrons, protons, neutrons, and neutrinos are all fermions and obey Fermi–Dirac statistics.

A fermion gas in which all energy states below some energy level are filled is called a fully degenerate fermion gas. The difference between this energy level and the lowest energy level is known as the Fermi energy. The electron gas in ordinary metals and in the interior of white dwarf stars constitute two examples of a degenerate electron gas. Most stars are supported against their own gravitation by normal thermal gas pressure. White dwarf stars are supported by the degeneracy pressure of the electron gas in their interior, while for neutron stars the degenerate particles are neutrons.

Electron degeneracy

In an ordinary fermion gas in which thermal effects dominate, most of the available electron energy levels are unfilled and the electrons are free to move to these states. As particle density is increased, electrons progressively fill the lower energy states and additional electrons are forced to occupy states of higher energy even at low temperatures. Degenerate gases strongly resist further compression because the electrons cannot move to already filled lower energy levels due to the Pauli exclusion principle. Since electrons cannot give up energy by moving to lower energy states, no thermal energy can be extracted. The momentum of the fermions in the fermion gas nevertheless generates pressure, termed degeneracy pressure.

Under high densities the matter becomes a degenerate gas when the electrons are all stripped from their parent atoms. In the core of a star, once hydrogen burning in nuclear fusion reactions stops, it becomes a collection of positively charged ions, largely helium and carbon nuclei, floating in a sea of electrons, which have been stripped from the nuclei. Degenerate gas is an almost perfect conductor of heat and does not obey the ordinary gas laws. White dwarfs are luminous not because they are generating any energy but rather because they have trapped a large amount of heat which is gradually radiated away. Normal gas exerts higher pressure when it is heated and expands, but the pressure in a degenerate gas does not depend on the temperature. When gas becomes super-compressed, particles position right up against each other to produce degenerate gas that behaves more like a solid. In degenerate gases the kinetic energies of electrons are quite high and the rate of collision between electrons and other particles is quite low, therefore degenerate electrons can travel great distances at velocities that approach the speed of light. Instead of temperature, the pressure in a degenerate gas depends only on the speed of the degenerate particles; however, adding heat does not increase the speed. Pressure is only increased by the mass of the particles, which increases the gravitational force pulling the particles closer together. Therefore, the phenomenon is the opposite of that normally found in matter where if the mass of the matter is increased, the object becomes bigger. In degenerate gas, when the mass is increased, the pressure is increased, and the particles become spaced closer together, so the object becomes smaller. Degenerate gas can be compressed to very high densities, typical values being in the range of 10,000 kilograms per cubic centimeter.

There is an upper limit to the mass of an electron-degenerate object, the Chandrasekhar limit, beyond which electron degeneracy pressure cannot support the object against collapse. The limit is approximately 1.44[7]solar masses for objects with compositions similar to the sun. The mass cutoff changes with the chemical composition of the object, as this affects the ratio of mass to number of electrons present. Celestial objects below this limit are white dwarf stars, formed by the collapse of the cores of stars that run out of fuel. During collapse, an electron-degenerate gas forms in the core, providing sufficient degeneracy pressure as it is compressed to resist further collapse. Above this mass limit, a neutron star (supported by neutron degeneracy pressure) or a black hole may be formed instead.

Proton degeneracy

Sufficiently dense matter containing protons experiences proton degeneracy pressure, in a manner similar to the electron degeneracy pressure in electron-degenerate matter: protons confined to a sufficiently small volume have a large uncertainty in their momentum due to the Heisenberg uncertainty principle. Because protons are much more massive than electrons, the same momentum represents a much smaller velocity for protons than for electrons. As a result, in matter with approximately equal numbers of protons and electrons, proton degeneracy pressure is much smaller than electron degeneracy pressure, and proton degeneracy is usually modeled as a correction to the equations of state of electron-degenerate matter.

Neutron degeneracy

Neutron degeneracy is analogous to electron degeneracy and is demonstrated in neutron stars, which are primarily supported by the pressure from a degenerate neutron gas.[8] This happens when a stellar core above 1.44[citation needed] solar masses, the Chandrasekhar limit, collapses and is not halted by the degenerate electrons. As the star collapses, the Fermi energy of the electrons increases to the point where it is energetically favorable for them to combine with protons to produce neutrons (via inverse beta decay, also termed electron capture and "neutralization"). The result of this collapse is an extremely compact star composed of nuclear matter, which is predominantly a degenerate neutron gas, sometimes called neutronium, with a small admixture of degenerate proton and electron gases.

Neutrons in a degenerate neutron gas are spaced much more closely than electrons in an electron-degenerate gas, because the more massive neutron has a much shorter wavelength at a given energy. In the case of neutron stars and white dwarf stars, this is compounded by the fact that the pressures within neutron stars are much higher than those in white dwarfs. The pressure increase is caused by the fact that the compactness of a neutron star causes gravitational forces to be much higher than in a less compact body with similar mass. This results in a star with a diameter on the order of a thousandth that of a white dwarf.

There is an upper limit to the mass of a neutron-degenerate object, the Tolman–Oppenheimer–Volkoff limit, which is analogous to the Chandrasekhar limit for electron-degenerate objects. The precise limit is unknown, as it depends on the equations of state of nuclear matter, for which a highly accurate model is not yet available. Above this limit, a neutron star may collapse into a black hole, or into other, denser forms of degenerate matter (such as quark matter) if these forms exist and have suitable properties (mainly related to degree of compressibility, or "stiffness", described by the equations of state).

Quark degeneracy

At densities greater than those supported by neutron degeneracy, quark matter is expected to occur. Several variations of this have been proposed that represent quark-degenerate states. Strange matter is a degenerate gas of quarks that is often assumed to contain strange quarks in addition to the usual up and down quarks. Color superconductor materials are degenerate gases of quarks in which quarks pair up in a manner similar to Cooper pairing in electrical superconductors. The equations of state for the various proposed forms of quark-degenerate matter vary widely, and are usually also poorly defined, due to the difficulty of modeling strong force interactions.

Quark-degenerate matter may occur in the cores of neutron stars, depending on the equations of state of neutron-degenerate matter. It may also occur in hypothetical quark stars, formed by the collapse of objects above the Tolman–Oppenheimer–Volkoff mass limit for neutron-degenerate objects. Whether quark-degenerate matter forms at all in these situations depends on the equations of state of both neutron-degenerate matter and quark-degenerate matter, both of which are poorly known.

Preon degeneracy hypothesis

Preons are subatomic particles proposed to be the constituents of quarks, which become composite particles in preon-based models. If preons exist, preon-degenerate matter might occur at densities greater than that which can be supported by quark-degenerate matter. The expected properties of preon-degenerate matter depend very strongly on the model chosen to describe preons, and the existence of preons is not assumed by the majority of the scientific community, due to conflicts between the preon models originally proposed and experimental data from particle accelerators.

Singularity

At densities greater than those supported by any degeneracy, gravity overwhelms all other forces. To the best of our current understanding, the body collapses to form a black hole. In the frame of reference that is co-moving with the collapsing matter, all the matter ends up in an infinitely dense singularity at the center of the event horizon. In the frame of reference of an observer at infinity, the collapse asymptotically approaches the event horizon.
As a consequence of relativity, the extreme gravitational field and orbital velocity experienced by infalling matter around a black hole would "slow" time for that matter relative to a distant observer.

at

Neutron star


From Wikipedia, the free encyclopedia

The size of a neutron star compared to Manhattan

Radiation from the pulsar PSR B1509-58, a rapidly spinning neutron star, makes nearby gas glow in X-rays (gold, from Chandra) and illuminates the rest of the nebula, here seen in infrared (blue and red, from WISE).

A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star after a supernova. Neutron stars are the densest and smallest stars known to exist in the universe; with a radius of only about 12–13 km (7 mi), they can have a mass of about two times that of the Sun.

Neutron stars are composed almost entirely of neutrons, which are subatomic particles without net electrical charge and with slightly larger mass than protons. Neutron stars are very hot and are supported against further collapse by quantum degeneracy pressure due to the phenomenon described by the Pauli exclusion principle, which states that no two neutrons (or any other fermionic particles) can occupy the same place and quantum state simultaneously.

A typical neutron star has a mass between ~1.4 and about 3 solar masses (M☉) with a surface temperature of ~6×105 K.[1][2][3][4][a] Neutron stars have overall densities of 3.7×1017 to 5.9×1017 kg/m3 (2.6×1014 to 4.1×1014 times the density of the Sun),[b] which is comparable to the approximate density of an atomic nucleus of 3×1017 kg/m3.[5] The neutron star's density varies from below 1×109 kg/m3 in the crust – increasing with depth – to above 6×1017 or 8×1017 kg/m3 deeper inside (denser than an atomic nucleus).[6] A normal-sized matchbox containing neutron star material would have a mass of approximately 5 billion tonnes or ~1 km3 of Earth rock.[citation needed]

In general, compact stars of less than 1.44 M☉ (the Chandrasekhar limit) are white dwarfs while compact stars weighing between that and 3 M☉ (the Tolman–Oppenheimer–Volkoff limit) should be neutron stars. The maximum observed mass of neutron stars is about 2 M☉. Compact stars with more than 10 M☉ will overcome the neutron degeneracy pressure and gravitational collapse will usually occur to produce a black hole.[7] The smallest observed mass of a black hole is about 5 M☉. Between these, hypothetical intermediate-mass stars such as quark stars and electroweak stars have been proposed, but none have been shown to exist. The equations of state of matter at such high densities are not precisely known because of the theoretical and empirical difficulties.

Some neutron stars rotate very rapidly (up to 716 times a second,[8][9] or approximately 43,000 revolutions per minute) and emit beams of electromagnetic radiation as pulsars. Indeed, the discovery of pulsars in 1967 first suggested that neutron stars exist. Gamma-ray bursts may be produced from rapidly rotating, high-mass stars that collapse to form a neutron star, or from the merger of binary neutron stars. There are thought to be on the order of 108 neutron stars in the galaxy, but they can only be easily detected in certain instances, such as if they are a pulsar or part of a binary system. Non-rotating and non-accreting neutron stars are virtually undetectable; however, the Hubble Space Telescope has observed one thermally radiating neutron star, called RX J185635-3754.

Formation

Any main sequence star with an initial mass of around 10 M☉ or above has the potential to become a neutron star. As the star evolves away from the main sequence, subsequent nuclear burning produces an iron-rich core. When all nuclear fuel in the core has been exhausted, the core must be supported by degeneracy pressure alone. Further deposits of material from shell burning cause the core to exceed the Chandrasekhar limit. Electron degeneracy pressure is overcome and the core collapses further, sending temperatures soaring to over 5×109 K. At these temperatures, photodisintegration (the breaking up of iron nuclei into alpha particles by high- energy gamma rays) occurs. As the temperature climbs even higher, electrons and protons combine to form neutrons, releasing a flood of neutrinos. When densities reach nuclear density of 4×1017 kg/m3, neutron degeneracy pressure halts the contraction. The infalling outer atmosphere of the star is flung outwards, becoming a Type II or Type Ib supernova.
The remnant left is a neutron star. If it has a mass greater than about 5 M☉, it collapses further to become a black hole. Other neutron stars are formed within close binaries.

As the core of a massive star is compressed during a Type II, Type Ib or Type Ic supernova, and collapses into a neutron star, it retains most of its angular momentum. Since it has only a tiny fraction of its parent's radius (and therefore its moment of inertia is sharply reduced), a neutron star is formed with very high rotation speed, and then gradually slows down. Neutron stars are known that have rotation periods from about 1.4 ms to 30 s. The neutron star's density also gives it very high surface gravity, with typical values ranging from 1012 to 1013 m/s2 (more than 1011 times of that of Earth).[4] One measure of such immense gravity is the fact that neutron stars have an escape velocity ranging from 100,000 km/s to 150,000 km/s, that is, from a third to half the speed of light. Matter falling onto the surface of a neutron star would be accelerated to tremendous speed by the star's gravity. The force of impact would likely destroy the object's component atoms, rendering all its matter identical, in most respects, to the rest of the star.

Properties


Gravitational light deflection at a neutron star. Due to relativistic light deflection more than half of the surface is visible (each chequered patch here represents 30 degrees by 30 degrees).[10] In natural units, the mass of the depicted star is 1 and its radius 4, or twice its Schwarzschild radius.[10]

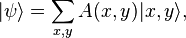
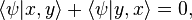
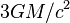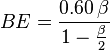
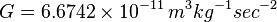
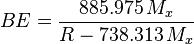
The gravitational field at the star's surface is about 2×1011 times stronger than on Earth. Such a strong gravitational field acts as a gravitational lens and bends the radiation emitted by the star such that parts of the normally invisible rear surface become visible.[10] If the radius of the neutron star is 3GM/c^2 or less, then the photons may be trapped in an orbit, thus making the whole surface of that neutron star visible, along with destabilizing orbits at that and less than that of the radius. A fraction of the mass of a star that collapses to form a neutron star is released in the supernova explosion from which it forms (from the law of mass-energy equivalence, E = mc2). The energy comes from the gravitational binding energy of a neutron star.

Neutron star relativistic equations of state provided by Jim Lattimer include a graph of radius vs. mass for various models.[11] The most likely radii for a given neutron star mass are bracketed by models AP4 (smallest radius) and MS2 (largest radius). BE is the ratio of gravitational binding energy mass equivalent to observed neutron star gravitational mass of "M" kilograms with radius "R" meters,[12]
BE = \frac{0.60\,\beta}{1 - \frac{\beta}{2}}      \beta \ = G\,M/R\,{c}^{2}
Given current values
G = 6.6742\times10^{-11}\, m^3kg^{-1}sec^{-2}[13]
c^2 = 8.98755\times10^{16}\, m^2sec^{-2}
M_{solar} = 1.98844\times10^{30}\, kg
and star masses "M" commonly reported as multiples of one solar mass,
M_x = \frac{M}{M_\odot}
then the relativistic fractional binding energy of a neutron star is
BE = \frac{885.975\,M_x}{R - 738.313\,M_x}
A 2 M☉ neutron star would not be more compact than 10,970 meters radius (AP4 model). Its mass fraction gravitational binding energy would then be 0.187, −18.7% (exothermic). This is not near 0.6/2 = 0.3, −30%.

A neutron star is so dense that one teaspoon (5 milliliters) of its material would have a mass over 5.5×1012 kg (that is 1100 tonnes per 1 nanolitre), about 900 times the mass of the Great Pyramid of Giza.[c] Hence, the gravitational force of a typical neutron star is such that if an object were to fall from a height of one meter, it would only take one microsecond to hit the surface of the neutron star, and would do so at around 2000 kilometers per second, or 7.2 million kilometers per hour.[14]

The temperature inside a newly formed neutron star is from around 1011 to 1012 kelvin.[6] However, the huge number of neutrinos it emits carry away so much energy that the temperature falls within a few years to around 106 kelvin.[6] Even at 1 million kelvin, most of the light generated by a neutron star is in X-rays.

The pressure increases from 3×1033 to 1.6×1035 Pa from the inner crust to the center.[15]
The equation of state for a neutron star is still not known. It is assumed that it differs significantly from that of a white dwarf, whose EOS is that of a degenerate gas which can be described in close agreement with special relativity. However, with a neutron star the increased effects of general relativity can no longer be ignored. Several EOS have been proposed (FPS, UU, APR, L, SLy, and others) and current research is still attempting to constrain the theories to make predictions of neutron star matter.[4][16] This means that the relation between density and mass is not fully known, and this causes uncertainties in radius estimates. For example, a 1.5 M☉ neutron star could have a radius of 10.7, 11.1, 12.1 or 15.1 kilometres (for EOS FPS, UU, APR or L respectively).[16]

Structure


Cross-section of neutron star. Densities are in terms of ρ0 the saturation nuclear matter density, where nucleons begin to touch.

Current understanding of the structure of neutron stars is defined by existing mathematical models, but it might be possible to infer through studies of neutron-star oscillations. Similar to asteroseismology for ordinary stars, the inner structure might be derived by analyzing observed frequency spectra of stellar oscillations.[4]

On the basis of current models, the matter at the surface of a neutron star is composed of ordinary atomic nuclei crushed into a solid lattice with a sea of electrons flowing through the gaps between them. It is possible that the nuclei at the surface are iron, due to iron's high binding energy per nucleon.[17] It is also possible that heavy element cores, such as iron, simply sink beneath the surface, leaving only light nuclei like helium and hydrogen cores.[17] If the surface temperature exceeds 106 kelvin (as in the case of a young pulsar), the surface should be fluid instead of the solid phase observed in cooler neutron stars (temperature <10 sup="">6
kelvin).[17]
The "atmosphere" of the star is hypothesized to be at most several micrometers thick, and its dynamic is fully controlled by the star's magnetic field. Below the atmosphere one encounters a solid "crust". This crust is extremely hard and very smooth (with maximum surface irregularities of ~5 mm), because of the extreme gravitational field.[18] The expected hierarchy of phases of nuclear matter in the inner crust has been characterized as nuclear pasta.[19]

Proceeding inward, one encounters nuclei with ever increasing numbers of neutrons; such nuclei would decay quickly on Earth, but are kept stable by tremendous pressures. As this process continues at increasing depths, neutron drip becomes overwhelming, and the concentration of free neutrons increases rapidly. In this region, there are nuclei, free electrons, and free neutrons. The nuclei become increasingly small (gravity and pressure overwhelming the strong force) until the core is reached, by definition the point where they disappear altogether.

The composition of the superdense matter in the core remains uncertain. One model describes the core as superfluid neutron-degenerate matter (mostly neutrons, with some protons and electrons). More exotic forms of matter are possible, including degenerate strange matter (containing strange quarks in addition to up and down quarks), matter containing high-energy pions and kaons in addition to neutrons,[4] or ultra-dense quark-degenerate matter.

History of discoveries


The first direct observation of a neutron star in visible light. The neutron star is RX J185635-3754.

In 1934, Walter Baade and Fritz Zwicky proposed the existence of the neutron star,[20][d] only a year after the discovery of the neutron by Sir James Chadwick.[23] In seeking an explanation for the origin of a supernova, they tentatively proposed that in supernova explosions ordinary stars are turned into stars that consist of extremely closely packed neutrons that they called neutron stars. Baade and Zwicky correctly proposed at that time that the release of the gravitational binding energy of the neutron stars powers the supernova: "In the supernova process, mass in bulk is annihilated". Neutron stars were thought to be too faint to be detectable and little work was done on them until November 1967, when Franco Pacini (1939–2012) pointed out that if the neutron stars were spinning and had large magnetic fields, then electromagnetic waves would be emitted. Unbeknown to him, radio astronomer Antony Hewish and his research assistant Jocelyn Bell at Cambridge were shortly to detect radio pulses from stars that are now believed to be highly magnetized, rapidly spinning neutron stars, known as pulsars.

In 1965, Antony Hewish and Samuel Okoye discovered "an unusual source of high radio brightness temperature in the Crab Nebula".[24] This source turned out to be the Crab Nebula neutron star that resulted from the great supernova of 1054.

In 1967, Iosif Shklovsky examined the X-ray and optical observations of Scorpius X-1 and correctly concluded that the radiation comes from a neutron star at the stage of accretion.[25]

In 1967, Jocelyn Bell and Antony Hewish discovered regular radio pulses from CP 1919. This pulsar was later interpreted as an isolated, rotating neutron star. The energy source of the pulsar is the rotational energy of the neutron star. The majority of known neutron stars (about 2000, as of 2010) have been discovered as pulsars, emitting regular radio pulses.

In 1971, Riccardo Giacconi, Herbert Gursky, Ed Kellogg, R. Levinson, E. Schreier, and H. Tananbaum discovered 4.8 second pulsations in an X-ray source in the constellation Centaurus, Cen X-3. They interpreted this as resulting from a rotating hot neutron star. The energy source is gravitational and results from a rain of gas falling onto the surface of the neutron star from a companion star or the interstellar medium.

In 1974, Antony Hewish was awarded the Nobel Prize in Physics "for his decisive role in the discovery of pulsars" without Jocelyn Bell who shared in the discovery.

In 1974, Joseph Taylor and Russell Hulse discovered the first binary pulsar, PSR B1913+16, which consists of two neutron stars (one seen as a pulsar) orbiting around their center of mass. Einstein's general theory of relativity predicts that massive objects in short binary orbits should emit gravitational waves, and thus that their orbit should decay with time. This was indeed observed, precisely as general relativity predicts, and in 1993, Taylor and Hulse were awarded the Nobel Prize in Physics for this discovery.

In 1982, Don Backer and colleagues discovered the first millisecond pulsar, PSR B1937+21. This objects spins 642 times per second, a value that placed fundamental constraints on the mass and radius of neutron stars. Many millisecond pulsars were later discovered, but PSR B1937+12 remained the fastest-spinning known pulsar for 24 years, until PSR J1748-2446ad was discovered.

In 2003, Marta Burgay and colleagues discovered the first double neutron star system where both components are detectable as pulsars, PSR J0737-3039. The discovery of this system allows a total of 5 different tests of general relativity, some of these with unprecedented precision.

In 2010, Paul Demorest and colleagues measured the mass of the millisecond pulsar PSR J1614–2230 to be 1.97±0.04 M☉, using Shapiro delay.[26] This was substantially higher than any previously measured neutron star mass (1.67 M☉, see PSR J1903+0327), and places strong constraints on the interior composition of neutron stars.
In 2013, John Antoniadis and colleagues measured the mass of PSR J0348+0432 to be 2.01±0.04 M☉, using white dwarf spectroscopy.[27] This confirmed the existence of such massive stars using a different method. Furthermore, this allowed, for the first time, a test of general relativity using such a massive neutron star.

Rotation

Neutron stars rotate extremely rapidly after their creation due to the conservation of angular momentum; like spinning ice skaters pulling in their arms, the slow rotation of the original star's core speeds up as it shrinks. A newborn neutron star can rotate several times a second; sometimes, the neutron star absorbs orbiting matter from a companion star, increasing the rotation to several hundred times per second, reshaping the neutron star into an oblate spheroid.

Over time, neutron stars slow down (spin down) because their rotating magnetic fields radiate energy; older neutron stars may take several seconds for each revolution.

The rate at which a neutron star slows its rotation is usually constant and very small: the observed rates of decline are between 10−10 and 10−21 seconds for each rotation. Therefore, for a typical slow down rate of 10−15 seconds per rotation, a neutron star now rotating in 1 second will rotate in 1.000003 seconds after a century, or 1.03 seconds after 1 million years.

NASA artist's conception of a "starquake", or "stellar quake".

Sometimes a neutron star will spin up or undergo a glitch, a sudden small increase of its rotation speed. Glitches are thought to be the effect of a starquake — as the rotation of the star slows down, the shape becomes more spherical. Due to the stiffness of the "neutron" crust, this happens as discrete events when the crust ruptures, similar to tectonic earthquakes. After the starquake, the star will have a smaller equatorial radius, and since angular momentum is conserved, rotational speed increases. Recent work, however, suggests that a starquake would not release sufficient energy for a neutron star glitch; it has been suggested that glitches may instead be caused by transitions of vortices in the superfluid core of the star from one metastable energy state to a lower one.[28]

Neutron stars have been observed to "pulse" radio and x-ray emissions believed to be caused by particle acceleration near the magnetic poles, which need not be aligned with the rotation axis of the star. Through mechanisms not yet entirely understood, these particles produce coherent beams of radio emission. External viewers see these beams as pulses of radiation whenever the magnetic pole sweeps past the line of sight. The pulses come at the same rate as the rotation of the neutron star, and thus, appear periodic. Neutron stars which emit such pulses are called pulsars.

The most rapidly rotating neutron star currently known, PSR J1748-2446ad, rotates at 716 rotations per second.[29] A recent paper reported the detection of an X-ray burst oscillation (an indirect measure of spin) at 1122 Hz from the neutron star XTE J1739-285.[30] However, at present, this signal has only been seen once, and should be regarded as tentative until confirmed in another burst from this star.

Population and distances

At present, there are about 2000 known neutron stars in the Milky Way and the Magellanic Clouds, the majority of which have been detected as radio pulsars. Neutron stars are mostly concentrated along the disk of the Milky Way although the spread perpendicular to the disk is large because the supernova explosion process can impart high speeds (400 km/s) to the newly created neutron star.

Some of the closest neutron stars are RX J1856.5-3754 about 400 light years away and PSR J0108-1431 at about 424 light years.[31] RX J1856.5-3754 is a member of a close group of neutron stars called The Magnificent Seven. Another nearby neutron star that was detected transiting the backdrop of the constellation Ursa Minor has been nicknamed Calvera by its Canadian and American discoverers, after the villain in the 1960 film The Magnificent Seven. This rapidly moving object was discovered using the ROSAT/Bright Source Catalog.

Binary neutron stars

About 5% of all known neutron stars are members of a binary system. The formation and evolution scenario of binary neutron stars is a rather exotic and complicated process.[32] The companion stars may be either ordinary stars, white dwarfs or other neutron stars. According to modern theories of binary evolution it is expected that neutron stars also exist in binary systems with black hole companions. Such binaries are expected to be prime sources for emitting gravitational waves. Neutron stars in binary systems often emit X-rays which is caused by the heating of material (gas) accreted from the companion star. Material from the outer layers of a (bloated) companion star is sucked towards the neutron star as a result of its very strong gravitational field. As a result of this process binary neutron stars may also coalesce into black holes if the accretion of mass takes place under extreme conditions.[33] It has been proposed that coalescence of binaries consisting of two neutron stars may be responsible for producing short gamma-ray bursts. Such events may also be responsible for creating all chemical elements beyond iron,[34] as opposed to the supernova nucleosynthesis theory.

Subtypes

Giant nucleus

A neutron star has some of the properties of an atomic nucleus, including density (within an order of magnitude) and being composed of nucleons. In popular scientific writing, neutron stars are therefore sometimes described as giant nuclei. However, in other respects, neutron stars and atomic nuclei are quite different. In particular, a nucleus is held together by the strong interaction, whereas a neutron star is held together by gravity, and thus the density and structure of neutron stars is more variable. It is generally more useful to consider such objects as stars.

Examples of neutron stars



at
Subscribe to: Posts (Atom)

Equality (mathematics)

From Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Equality_...

  • Islamic State and the Levant
    From Wikipedia, the free encyclopedia Islamic State of Iraq and the Levant الدولة الإسلامية في العراق والشام   ( ...
  • Heart Sutra
    From Wikipedia, the free encyclopedia A reproduction of the palm -leaf manuscript in Siddham script ...
  • Slum
    From Wikipedia, the free encyclopedia ...