Chemical bond

From Wikipedia, the free encyclopedia

A chemical bond is a lasting attraction between atoms, ions or molecules that enables the formation of chemical compounds. The bond may result from the electrostatic force of attraction between oppositely charged ions as in ionic bonds; or through the sharing of electrons as in covalent bonds. The strength of chemical bonds varies considerably; there are "strong bonds" or "primary bond" such as metallic, covalent or ionic bonds and "weak bonds" or "secondary bond" such as dipole–dipole interactions, the London dispersion force and hydrogen bonding.

Since opposite charges attract via a simple electromagnetic force, the negatively charged electrons that are orbiting the nucleus and the positively charged protons in the nucleus attract each other. An electron positioned between two nuclei will be attracted to both of them, and the nuclei will be attracted toward electrons in this position. This attraction constitutes the chemical bond. Due to the matter wave nature of electrons and their smaller mass, they must occupy a much larger amount of volume compared with the nuclei, and this volume occupied by the electrons keeps the atomic nuclei in a bond relatively far apart, as compared with the size of the nuclei themselves.

In general, strong chemical bonding is associated with the sharing or transfer of electrons between the participating atoms. The atoms in molecules, crystals, metals and diatomic gases—indeed most of the physical environment around us—are held together by chemical bonds, which dictate the structure and the bulk properties of matter.

Examples of Lewis dot-style representations of chemical bonds between carbon (C), hydrogen (H), and oxygen (O). Lewis dot diagrams were an early attempt to describe chemical bonding and are still widely used today.

All bonds can be explained by quantum theory, but, in practice, simplification rules allow chemists to predict the strength, directionality, and polarity of bonds. The octet rule and VSEPR theory are two examples. More sophisticated theories are valence bond theory which includes orbital hybridization and resonance, and molecular orbital theory which includes linear combination of atomic orbitals and ligand field theory. Electrostatics are used to describe bond polarities and the effects they have on chemical substances.

Overview of main types of chemical bonds

A chemical bond is an attraction between atoms. This attraction may be seen as the result of different behaviors of the outermost or valence electrons of atoms. These behaviors merge into each other seamlessly in various circumstances, so that there is no clear line to be drawn between them. However it remains useful and customary to differentiate between different types of bond, which result in different properties of condensed matter.

In the simplest view of a covalent bond, one or more electrons (often a pair of electrons) are drawn into the space between the two atomic nuclei. Energy is released by bond formation. This is not as a reduction in potential energy, because the attraction of the two electrons to the two protons is offset by the electron-electron and proton-proton repulsions. Instead, the release of energy (and hence stability of the bond) arises from the reduction in kinetic energy due to the electrons being in a more spatially distributed (i.e. longer de Broglie wavelength) orbital compared with each electron being confined closer to its respective nucleus.^[1] These bonds exist between two particular identifiable atoms and have a direction in space, allowing them to be shown as single connecting lines between atoms in drawings, or modeled as sticks between spheres in models.

In a polar covalent bond, one or more electrons are unequally shared between two nuclei. Covalent bonds often result in the formation of small collections of better-connected atoms called molecules, which in solids and liquids are bound to other molecules by forces that are often much weaker than the covalent bonds that hold the molecules internally together. Such weak intermolecular bonds give organic molecular substances, such as waxes and oils, their soft bulk character, and their low melting points (in liquids, molecules must cease most structured or oriented contact with each other). When covalent bonds link long chains of atoms in large molecules, however (as in polymers such as nylon), or when covalent bonds extend in networks through solids that are not composed of discrete molecules (such as diamond or quartz or the silicate minerals in many types of rock) then the structures that result may be both strong and tough, at least in the direction oriented correctly with networks of covalent bonds. Also, the melting points of such covalent polymers and networks increase greatly.

In a simplified view of an ionic bond, the bonding electron is not shared at all, but transferred. In this type of bond, the outer atomic orbital of one atom has a vacancy which allows the addition of one or more electrons. These newly added electrons potentially occupy a lower energy-state (effectively closer to more nuclear charge) than they experience in a different atom. Thus, one nucleus offers a more tightly bound position to an electron than does another nucleus, with the result that one atom may transfer an electron to the other. This transfer causes one atom to assume a net positive charge, and the other to assume a net negative charge. The bond then results from electrostatic attraction between atoms and the atoms become positive or negatively charged ions. Ionic bonds may be seen as extreme examples of polarization in covalent bonds. Often, such bonds have no particular orientation in space, since they result from equal electrostatic attraction of each ion to all ions around them. Ionic bonds are strong (and thus ionic substances require high temperatures to melt) but also brittle, since the forces between ions are short-range and do not easily bridge cracks and fractures. This type of bond gives rise to the physical characteristics of crystals of classic mineral salts, such as table salt.

A less often mentioned type of bonding is metallic bonding. In this type of bonding, each atom in a metal donates one or more electrons to a "sea" of electrons that reside between many metal atoms. In this sea, each electron is free (by virtue of its wave nature) to be associated with a great many atoms at once. The bond results because the metal atoms become somewhat positively charged due to loss of their electrons while the electrons remain attracted to many atoms, without being part of any given atom. Metallic bonding may be seen as an extreme example of delocalization of electrons over a large system of covalent bonds, in which every atom participates. This type of bonding is often very strong (resulting in the tensile strength of metals). However, metallic bonding is more collective in nature than other types, and so they allow metal crystals to more easily deform, because they are composed of atoms attracted to each other, but not in any particularly-oriented ways. This results in the malleability of metals. The cloud of electrons in metallic bonding causes the characteristically good electrical and thermal conductivity of metals, and also their shiny lustre that reflects most frequencies of white light.

History

Early speculations about the nature of the chemical bond, from as early as the 12th century, supposed that certain types of chemical species were joined by a type of chemical affinity. In 1704, Sir Isaac Newton famously outlined his atomic bonding theory, in "Query 31" of his Opticks, whereby atoms attach to each other by some "force". Specifically, after acknowledging the various popular theories in vogue at the time, of how atoms were reasoned to attach to each other, i.e. "hooked atoms", "glued together by rest", or "stuck together by conspiring motions", Newton states that he would rather infer from their cohesion, that "particles attract one another by some force, which in immediate contact is exceedingly strong, at small distances performs the chemical operations, and reaches not far from the particles with any sensible effect."

In 1819, on the heels of the invention of the voltaic pile, Jöns Jakob Berzelius developed a theory of chemical combination stressing the electronegative and electropositive characters of the combining atoms. By the mid 19th century, Edward Frankland, F.A. Kekulé, A.S. Couper, Alexander Butlerov, and Hermann Kolbe, building on the theory of radicals, developed the theory of valency, originally called "combining power", in which compounds were joined owing to an attraction of positive and negative poles. In 1916, chemist Gilbert N. Lewis developed the concept of the electron-pair bond, in which two atoms may share one to six electrons, thus forming the single electron bond, a single bond, a double bond, or a triple bond; in Lewis's own words, "An electron may form a part of the shell of two different atoms and cannot be said to belong to either one exclusively."^[2]

That same year, Walther Kossel put forward a theory similar to Lewis' only his model assumed complete transfers of electrons between atoms, and was thus a model of ionic bonding. Both Lewis and Kossel structured their bonding models on that of Abegg's rule (1904).

Niels Bohr proposed a model of the atom and a model of the chemical bond. According to his model for a diatomic molecule, the electrons of the atoms of the molecule form a rotating ring whose plane is perpendicular to the axis of the molecule and equidistant from the atomic nuclei. The dynamic equilibrium of the molecular system is achieved through the balance of forces between the forces of attraction of nuclei to the plane of the ring of electrons and the forces of mutual repulsion of the nuclei. The Bohr model of the chemical bond took into account the Coulomb repulsion - the electrons in the ring are at the maximum distance from each other.^[3][4]

In 1927, the first mathematically complete quantum description of a simple chemical bond, i.e. that produced by one electron in the hydrogen molecular ion, H₂⁺, was derived by the Danish physicist Oyvind Burrau.^[5] This work showed that the quantum approach to chemical bonds could be fundamentally and quantitatively correct, but the mathematical methods used could not be extended to molecules containing more than one electron. A more practical, albeit less quantitative, approach was put forward in the same year by Walter Heitler and Fritz London. The Heitler–London method forms the basis of what is now called valence bond theory. In 1929, the linear combination of atomic orbitals molecular orbital method (LCAO) approximation was introduced by Sir John Lennard-Jones, who also suggested methods to derive electronic structures of molecules of F₂ (fluorine) and O₂ (oxygen) molecules, from basic quantum principles. This molecular orbital theory represented a covalent bond as an orbital formed by combining the quantum mechanical Schrödinger atomic orbitals which had been hypothesized for electrons in single atoms. The equations for bonding electrons in multi-electron atoms could not be solved to mathematical perfection (i.e., analytically), but approximations for them still gave many good qualitative predictions and results. Most quantitative calculations in modern quantum chemistry use either valence bond or molecular orbital theory as a starting point, although a third approach, density functional theory, has become increasingly popular in recent years.

In 1933, H. H. James and A. S. Coolidge carried out a calculation on the dihydrogen molecule that, unlike all previous calculation which used functions only of the distance of the electron from the atomic nucleus, used functions which also explicitly added the distance between the two electrons.^[6] With up to 13 adjustable parameters they obtained a result very close to the experimental result for the dissociation energy. Later extensions have used up to 54 parameters and gave excellent agreement with experiments. This calculation convinced the scientific community that quantum theory could give agreement with experiment. However this approach has none of the physical pictures of the valence bond and molecular orbital theories and is difficult to extend to larger molecules.

Bonds in chemical formulas

Because atoms and molecules are three-dimensional, it is difficult to use a single method to indicate orbitals and bonds. In molecular formulas the chemical bonds (binding orbitals) between atoms are indicated in different ways depending on the type of discussion. Sometimes, some details are neglected. For example, in organic chemistry one is sometimes concerned only with the functional group of the molecule. Thus, the molecular formula of ethanol may be written in conformational form, three-dimensional form, full two-dimensional form (indicating every bond with no three-dimensional directions), compressed two-dimensional form (CH₃–CH₂–OH), by separating the functional group from another part of the molecule (C₂H₅OH), or by its atomic constituents (C₂H₆O), according to what is discussed. Sometimes, even the non-bonding valence shell electrons (with the two-dimensional approximate directions) are marked, e.g. for elemental carbon _.^'C^'. Some chemists may also mark the respective orbitals, e.g. the hypothetical ethene⁻⁴ anion (_\^/C=C_/^{\ −4}) indicating the possibility of bond formation.

Strong chemical bonds

Strong chemical bonds are the intramolecular forces which hold atoms together in molecules. A strong chemical bond is formed from the transfer or sharing of electrons between atomic centers and relies on the electrostatic attraction between the protons in nuclei and the electrons in the orbitals.

The types of strong bond differ due to the difference in electronegativity of the constituent elements. A large difference in electronegativity leads to more polar (ionic) character in the bond.

Ionic bond

Ionic bonding is a type of electrostatic interaction between atoms which have a large electronegativity difference. There is no precise value that distinguishes ionic from covalent bonding, but a difference of electronegativity of over 1.7 is likely to be ionic, and a difference of less than 1.7 is likely to be covalent.^[8] Ionic bonding leads to separate positive and negative ions. Ionic charges are commonly between −3e to +3e. Ionic bonding commonly occurs in metal salts such as sodium chloride (table salt). A typical feature of ionic bonds is that the species form into ionic crystals, in which no ion is specifically paired with any single other ion, in a specific directional bond. Rather, each species of ion is surrounded by ions of the opposite charge, and the spacing between it and each of the oppositely charged ions near it, is the same for all surrounding atoms of the same type. It is thus no longer possible to associate an ion with any specific other single ionized atom near it. This is a situation unlike that in covalent crystals, where covalent bonds between specific atoms are still discernible from the shorter distances between them, as measured via such techniques as X-ray diffraction.

Ionic crystals may contain a mixture of covalent and ionic species, as for example salts of complex acids, such as sodium cyanide, NaCN. X-ray diffraction shows that in NaCN, for example, the bonds between sodium cations (Na⁺) and the cyanide anions (CN⁻) are ionic, with no sodium ion associated with any particular cyanide. However, the bonds between C and N atoms in cyanide are of the covalent type, so that each carbon is strongly bound to just one nitrogen, to which it is physically much closer than it is to other carbons or nitrogens in a sodium cyanide crystal.

When such crystals are melted into liquids, the ionic bonds are broken first because they are non-directional and allow the charged species to move freely. Similarly, when such salts dissolve into water, the ionic bonds are typically broken by the interaction with water, but the covalent bonds continue to hold. For example, in solution, the cyanide ions, still bound together as single CN⁻ ions, move independently through the solution, as do sodium ions, as Na⁺. In water, charged ions move apart because each of them are more strongly attracted to a number of water molecules, than to each other. The attraction between ions and water molecules in such solutions is due to a type of weak dipole-dipole type chemical bond. In melted ionic compounds, the ions continue to be attracted to each other, but not in any ordered or crystalline way.

Covalent bond

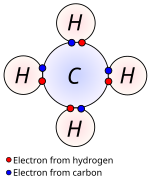
Nonpolar covalent bonds in methane (CH₄). The Lewis structure shows electrons shared between C and H atoms.

Covalent bonding is a common type of bonding, in which two or more atoms share valence electrons more or less equally. The simplest and most common type is a single bond in which two atoms share two electrons. Other types include the double bond, the triple bond, one- and three-electron bonds, the three-center two-electron bond and three-center four-electron bond.

In nonpolar covalent bonds, the electronegativity difference between the bonded atoms is small, typically 0 to 0.3. Bonds within most organic compounds are described as covalent. The figure shows methane (CH₄), in which each hydrogen forms a covalent bond with the carbon.

Molecules which are formed primarily from non-polar covalent bonds are often immiscible in water or other polar solvents, but much more soluble in non-polar solvents such as hexane.

A polar covalent bond is a covalent bond with a significant ionic character. This means that the two shared electrons are closer to one of the atoms than the other, creating an imbalance of charge. Such bonds occur between two atoms with moderately different electronegativities and give rise to dipole–dipole interactions. The electronegativity difference between the two atoms in these bonds is 0.3 to 1.7.

Single and multiple bonds

A single bond between two atoms corresponds to the sharing of one pair of electrons. The electron density of these two bonding electrons is concentrated in the region between the two atoms, which is the defining quality of a sigma bond.

Two p-orbitals forming a pi-bond.

A double bond between two atoms is formed by the sharing of two pairs of electrons, one in a sigma bond and one in a pi bond, with electron density concentrated on two opposite sides of the internuclear axis. A triple bond consists of three shared electron pairs, forming one sigma and two pi bonds.

Quadruple and higher bonds are very rare and occur only between certain transition metal atoms.

Coordinate covalent bond (Dipolar bond)

Adduct of ammonia and boron trifluoride

A coordinate covalent bond is a covalent bond in which the two shared bonding electrons are from the same one of the atoms involved in the bond. For example, boron trifluoride (BF₃) and ammonia (NH₃) from an adduct or coordination complex F₃B←NH₃ with a B–N bond in which a lone pair of electrons on N is shared with an empty atomic orbital on B. BF₃ with an empty orbital is described as an electron pair acceptor or Lewis acid, while NH₃ with a lone pair which can be shared is described as an electron-pair donor or Lewis base. The electrons are shared roughly equally between the atoms in contrast to ionic bonding. Such bonding is shown by an arrow pointing to the Lewis acid.

Transition metal complexes are generally bound by coordinate covalent bonds. For example, the ion Ag⁺ reacts as a Lewis acid with two molecules of the Lewis base NH₃ to form the complex ion Ag(NH₃)₂⁺, which has two Ag←N coordinate covalent bonds.

Metallic bonding

In metallic bonding, bonding electrons are delocalized over a lattice of atoms. By contrast, in ionic compounds, the locations of the binding electrons and their charges are static. The freely-moving or delocalization of bonding electrons leads to classical metallic properties such as luster (surface light reflectivity), electrical and thermal conductivity, ductility, and high tensile strength.

Intermolecular bonding

There are four basic types of bonds that can be formed between two or more (otherwise non-associated) molecules, ions or atoms. Intermolecular forces cause molecules to be attracted or repulsed by each other. Often, these define some of the physical characteristics (such as the melting point) of a substance.

• A large difference in electronegativity between two bonded atoms will cause a permanent charge separation, or dipole, in a molecule or ion. Two or more molecules or ions with permanent dipoles can interact within dipole-dipole interactions. The bonding electrons in a molecule or ion will, on average, be closer to the more electronegative atom more frequently than the less electronegative one, giving rise to partial charges on each atom, and causing electrostatic forces between molecules or ions.
• A hydrogen bond is effectively a strong example of an interaction between two permanent dipoles. The large difference in electronegativities between hydrogen and any of fluorine, nitrogen and oxygen, coupled with their lone pairs of electrons cause strong electrostatic forces between molecules. Hydrogen bonds are responsible for the high boiling points of water and ammonia with respect to their heavier analogues.
• The London dispersion force arises due to instantaneous dipoles in neighbouring atoms. As the negative charge of the electron is not uniform around the whole atom, there is always a charge imbalance. This small charge will induce a corresponding dipole in a nearby molecule; causing an attraction between the two. The electron then moves to another part of the electron cloud and the attraction is broken.
• A cation–pi interaction occurs between a pi bond and a cation.

Theories of chemical bonding

In the (unrealistic) limit of "pure" ionic bonding, electrons are perfectly localized on one of the two atoms in the bond. Such bonds can be understood by classical physics. The forces between the atoms are characterized by isotropic continuum electrostatic potentials. Their magnitude is in simple proportion to the charge difference.

Covalent bonds are better understood by valence bond theory or molecular orbital theory. The properties of the atoms involved can be understood using concepts such as oxidation number. The electron density within a bond is not assigned to individual atoms, but is instead delocalized between atoms. In valence bond theory, the two electrons on the two atoms are coupled together with the bond strength depending on the overlap between them. In molecular orbital theory, the linear combination of atomic orbitals (LCAO) helps describe the delocalized molecular orbital structures and energies based on the atomic orbitals of the atoms they came from. Unlike pure ionic bonds, covalent bonds may have directed anisotropic properties. These may have their own names, such as sigma bond and pi bond.

In the general case, atoms form bonds that are intermediate between ionic and covalent, depending on the relative electronegativity of the atoms involved. This type of bond is sometimes called polar covalent.

Nuclear binding energy

From Wikipedia, the free encyclopedia

Nuclear binding energy is the minimum energy that would be required to disassemble the nucleus of an atom into its component parts. These component parts are neutrons and protons, which are collectively called nucleons. The binding is always a positive number, as we need to spend energy in moving the nucleons away from each other (attracted by strong nuclear force). The mass of an atomic nucleus is less than the sum of the individual masses of the free constituent protons and neutrons (according to Einstein's equation E=mc²) and this 'missing mass' is known as the mass defect, and represents the energy that was released when the nucleus was formed.

The term "nuclear binding energy" may also refer to the energy balance in processes in which the nucleus splits into fragments composed of more than one nucleon. If new binding energy is available when light nuclei fuse, or when heavy nuclei split, either process can result in release of this binding energy. This energy may be made available as nuclear energy and can be used to produce electricity as in (nuclear power) or in a nuclear weapon. When a large nucleus splits into pieces, excess energy is emitted as photons (gamma rays) and as the kinetic energy of a number of different ejected particles (nuclear fission products).

The nuclear binding energies and forces are on the order of a million times greater than the electron binding energies of light atoms like hydrogen.^[1]

The mass defect of a nucleus represents the mass of the energy of binding of the nucleus, and is the difference between the mass of a nucleus and the sum of the masses of the nucleons of which it is composed.^[2]

Introduction

Nuclear binding energy is explained by the basic principles involved in nuclear physics.

Nuclear energy

An absorption or release of nuclear energy occurs in nuclear reactions or radioactive decay; those that absorb energy are called endothermic reactions and those that release energy are exothermic reactions. Energy is consumed or liberated because of differences in the nuclear binding energy between the incoming and outgoing products of the nuclear transmutation.^[3]

The best-known classes of exothermic nuclear transmutations are fission and fusion. Nuclear energy may be liberated by atomic fission, when heavy atomic nuclei (like uranium and plutonium) are broken apart into lighter nuclei. The energy from fission is used to generate electric power in hundreds of locations worldwide. Nuclear energy is also released during atomic fusion, when light nuclei like hydrogen are combined to form heavier nuclei such as helium. The Sun and other stars use nuclear fusion to generate thermal energy which is later radiated from the surface, a type of stellar nucleosynthesis. In any exothermic nuclear process, nuclear mass might ultimately be converted to thermal energy, given off as heat.

In order to quantify the energy released or absorbed in any nuclear transmutation, one must know the nuclear binding energies of the nuclear components involved in the transmutation.

The nuclear force

Electrons and nuclei are kept together by electrostatic attraction (negative attracts positive). Furthermore, electrons are sometimes shared by neighboring atoms or transferred to them (by processes of quantum physics), and this link between atoms is referred to as a chemical bond, and is responsible for the formation of all chemical compounds.^[4]

The force of electric attraction does not hold nuclei together, because all protons carry a positive charge and repel each other. Thus, electric forces do not hold nuclei together, because they act in the opposite direction. It has been established that binding neutrons to nuclei clearly requires a non-electrical attraction.^[4]

Therefore, another force, called the nuclear force (or residual strong force) holds the nucleons of nuclei together. This force is a residuum of the strong interaction, which binds quarks into nucleons at an even smaller level of distance.

The nuclear force must be stronger than the electric repulsion at short distances, but weaker far away, or else different nuclei might tend to clump together. Therefore, it has short-range characteristics. An analogy to the nuclear force is the force between two small magnets: magnets are very difficult to separate when stuck together, but once pulled a short distance apart, the force between them drops almost to zero.^[4]

Unlike gravity or electrical forces, the nuclear force is effective only at very short distances. At greater distances, the electrostatic force dominates: the protons repel each other because they are positively charged, and like charges repel. For that reason, the protons forming the nuclei of ordinary hydrogen—for instance, in a balloon filled with hydrogen—do not combine to form helium (a process that also would require some protons to combine with electrons and become neutrons). They cannot get close enough for the nuclear force, which attracts them to each other, to become important. Only under conditions of extreme pressure and temperature (for example, within the core of a star), can such a process take place.^[5]

Physics of nuclei

There are around 94 naturally occurring elements on earth. The atoms of each element have a nucleus containing a specific number of protons (always the same number for a given element), and some number of neutrons, which is often roughly a similar number. Two atoms of the same element having different numbers of neutrons are known as isotopes of the element. Different isotopes may have different properties - for example one might be stable and another might be unstable, and gradually undergo radioactive decay to become another element.

The hydrogen nucleus contain just one proton, Its isotope deuterium, or heavy hydrogen, contains a proton and a neutron. Helium contains two protons and two neutrons, and carbon, nitrogen and oxygen - six, seven and eight of each particle, respectively. However, a helium nucleus weighs less than the sum of the weights of the two hydrogen nuclei which combine to make it. The same is true for carbon, nitrogen and oxygen. For example, the carbon nucleus is slightly lighter than three helium nuclei, which can combine to make a carbon nucleus. This difference is known as the mass defect.

Mass defect

Mass defect (not to be confused with mass excess in nuclear physics or mass defect in mass spectrometry) is the difference between the mass of a composite particle and the sum of the masses of its parts. For example, a helium atom containing 4 nucleons has a mass about 0.8% less than the total mass of four hydrogen nuclei (which contain one nucleon each).

The "mass defect" can be explained using Albert Einstein's formula E = mc², describing the equivalence of energy and mass. By this formula, adding energy also increases mass (both weight and inertia), whereas removing energy decreases mass. In the above example, the helium nucleus has four nucleons bound together, and the binding energy which holds them together is, in effect, the missing 0.8% of mass.

If a combination of particles contains extra energy—for instance, in a molecule of the explosive TNT—weighing it reveals some extra mass, compared to its end products after an explosion. (The weighing must be done after the products have been stopped and cooled, however, as the extra mass must escape from the system as heat before its loss can be noticed, in theory.) On the other hand, if one must inject energy to separate a system of particles into its components, then the initial mass is less than that of the components after they are separated. In the latter case, the energy injected is "stored" as potential energy, which shows as the increased mass of the components that store it. This is an example of the fact that energy of all types is seen in systems as mass, since mass and energy are equivalent, and each is a "property" of the other.^[6]

The latter scenario is the case with nuclei such as helium: to break them up into protons and neutrons, one must inject energy. On the other hand, if a process existed going in the opposite direction, by which hydrogen atoms could be combined to form helium, then energy would be released. The energy can be computed using E = Δm c² for each nucleus, where Δm is the difference between the mass of the helium nucleus and the mass of four protons (plus two electrons, absorbed to create the neutrons of helium).

For lighter elements, the energy that can be released by assembling them from lighter elements decreases, and energy can be released when they fuse. This is true for nuclei lighter that iron/nickel. For heavier nuclei, more energy is needed to bind them, to the point that energy is released by breaking them up into 2 fragments (known as atomic fission). Nuclear power is generated at present by breaking up uranium nuclei in nuclear power reactors, and capturing the released energy as heat, which is converted to electricity.

As a rule, very light elements can fuse comparatively easily, and very heavy elements can break up via fission very easily; elements in the middle are more stable and it is difficult to make them undergo either fusion or fission in an earthly environment such as a laboratory.

The reason the trend reverses after iron is the growing positive charge of the nuclei, which tends to force nuclei to break up. It is resisted by the strong nuclear interaction, which holds nucleons together. The electric force may be weaker than the strong nuclear force, but the strong force has a much more limited range: in an iron nucleus, each proton repels the other 25 protons, while the nuclear force only binds close neighbors. So for larger nuclei, the electrostatic forces tend to dominate and the nucleus will tend over time to break up.

As nuclei grow bigger still, this disruptive effect becomes steadily more significant. By the time polonium is reached (84 protons), nuclei can no longer accommodate their large positive charge, but emit their excess protons quite rapidly in the process of alpha radioactivity—the emission of helium nuclei, each containing two protons and two neutrons. (Helium nuclei are an especially stable combination.) Because of this process, nuclei with more than 94 protons are not found naturally on Earth (see periodic table). The isotopes beyond uranium (atomic number 92) with the longest half-lives are plutonium-244 (80 million years) and curium-247 (16 million years).

Solar binding energy

The nuclear fusion process works as follows: five billion years ago, the new Sun formed when gravity pulled together a vast cloud of hydrogen and dust, from which the Earth and other planets also arose. The gravitational pull released energy and heated the early Sun, much in the way Helmholtz proposed.

Thermal energy appears as the motion of atoms and molecules: the higher the temperature of a collection of particles, the greater is their velocity and the more violent are their collisions. When the temperature at the center of the newly formed Sun became great enough for collisions between hydrogen nuclei to overcome their electric repulsion, and bring them into the short range of the attractive nuclear force, nuclei began to stick together. When this began to happen, protons combined into deuterium and then helium, with some protons changing in the process to neutrons (plus positrons, positive electrons, which combine with electrons and become neutral). This released nuclear energy now keeps up the high temperature of the Sun's core, and the heat also keeps the gas pressure high, keeping the Sun at its present size, and stopping gravity from compressing it any more. There is now a stable balance between gravity and pressure.

Different nuclear reactions may predominate at different stages of the Sun's existence, including the proton-proton reaction and the carbon-nitrogen cycle—which involves heavier nuclei, but whose final product is still the combination of protons to form helium.

A branch of physics, the study of controlled nuclear fusion, has tried since the 1950s to derive useful power from nuclear fusion reactions that combine small nuclei into bigger ones, typically to heat boilers, whose steam could turn turbines and produce electricity. Unfortunately, no earthly laboratory can match one feature of the solar powerhouse: the great mass of the Sun, whose weight keeps the hot plasma compressed and confines the nuclear furnace to the Sun's core. Instead, physicists use strong magnetic fields to confine the plasma, and for fuel they use heavy forms of hydrogen, which burn more easily. Magnetic traps can be rather unstable, and any plasma hot enough and dense enough to undergo nuclear fusion tends to slip out of them after a short time. Even with ingenious tricks, the confinement in most cases lasts only a small fraction of a second.

Combining nuclei

Small nuclei that are larger than hydrogen can combine into bigger ones and release energy, but in combining such nuclei, the amount of energy released is much smaller compared to hydrogen fusion. The reason is that while the overall process releases energy from letting the nuclear attraction do its work, energy must first be injected to force together positively charged protons, which also repel each other with their electric charge.^[5]

For elements that weigh more than iron (a nucleus with 26 protons), the fusion process no longer releases energy. In even heavier nuclei energy is consumed, not released, by combining similar sized nuclei. With such large nuclei, overcoming the electric repulsion (which affects all protons in the nucleus) requires more energy than what is released by the nuclear attraction (which is effective mainly between close neighbors). Conversely, energy could actually be released by breaking apart nuclei heavier than iron.^[5]

With the nuclei of elements heavier than lead, the electric repulsion is so strong that some of them spontaneously eject positive fragments, usually nuclei of helium that form very stable combinations (alpha particles). This spontaneous break-up is one of the forms of radioactivity exhibited by some nuclei.^[5]

Nuclei heavier than lead (except for bismuth, thorium, and uranium) spontaneously break up too quickly to appear in nature as primordial elements, though they can be produced artificially or as intermediates in the decay chains of lighter elements. Generally, the heavier the nuclei are, the faster they spontaneously decay.^[5]

Iron nuclei are the most stable nuclei (in particular iron-56), and the best sources of energy are therefore nuclei whose weights are as far removed from iron as possible. One can combine the lightest ones—nuclei of hydrogen (protons)—to form nuclei of helium, and that is how the Sun generates its energy. Or else one can break up the heaviest ones—nuclei of uranium or plutonium—into smaller fragments, and that is what nuclear power reactors do.^[5]

Nuclear binding energy

An example that illustrates nuclear binding energy is the nucleus of ¹²C (carbon-12), which contains 6 protons and 6 neutrons. The protons are all positively charged and repel each other, but the nuclear force overcomes the repulsion and causes them to stick together. The nuclear force is a close-range force (it is strongly attractive at a distance of 1.0 fm and becomes extremely small beyond a distance of 2.5fm), and virtually no effect of this force is observed outside the nucleus. The nuclear force also pulls neutrons together, or neutrons and protons.^[7]

The energy of the nucleus is negative with regard to the energy of the particles pulled apart to infinite distance (just like the gravitational energy of planets of the solar system), because energy must be utilized to split a nucleus into its individual protons and neutrons. Mass spectrometers have measured the masses of nuclei, which are always less than the sum of the masses of protons and neutrons that form them, and the difference—by the formula E = m c²—gives the binding energy of the nucleus.^[7]

Nuclear fusion

The binding energy of helium is the energy source of the Sun and of most stars. The sun is composed of 74 percent hydrogen (measured by mass), an element whose nucleus is a single proton. Energy is released in the sun when 4 protons combine into a helium nucleus, a process in which two of them are also converted to neutrons.^[7]

The conversion of protons to neutrons is the result of another nuclear force, known as the weak (nuclear) force. The weak force, like the strong force, has a short range, but is much weaker than the strong force. The weak force tries to make the number of neutrons and protons into the most energetically stable configuration. For nuclei containing less than 40 particles, these numbers are usually about equal. Protons and neutrons are closely related and are collectively known as nucleons. As the number of particles increases toward a maximum of about 209, the number of neutrons to maintain stability begins to outstrip the number of protons, until the ratio of neutrons to protons is about three to two.^[7]

The protons of hydrogen combine to helium only if they have enough velocity to overcome each other's mutual repulsion sufficiently to get within range of the strong nuclear attraction. This means that fusion only occurs within a very hot gas. Hydrogen hot enough for combining to helium requires an enormous pressure to keep it confined, but suitable conditions exist in the central regions of the Sun, where such pressure is provided by the enormous weight of the layers above the core, pressed inwards by the Sun's strong gravity. The process of combining protons to form helium is an example of nuclear fusion.^[7]

The earth's oceans contain a large amount of hydrogen that could theoretically be used for fusion, and helium byproduct of fusion does not harm the environment, so some consider nuclear fusion a good alternative to supply humanity's energy needs. Experiments to generate electricity from fusion have so far only partially succeeded. Sufficiently hot hydrogen must be ionized and confined. One technique is to use very strong magnetic fields, because charged particles (like those trapped in the Earth's radiation belt) are guided by magnetic field lines. Fusion experiments also rely on heavy hydrogen, which fuses more easily, and gas densities can be moderate. But even with these techniques far more net energy is consumed by the fusion experiments than is yielded by the process.^[7]

The binding energy maximum and ways to approach it by decay

In the main isotopes of light nuclei, such as carbon, nitrogen and oxygen, the most stable combination of neutrons and of protons are when the numbers are equal (this continues to element 20, calcium). However, in heavier nuclei, the disruptive energy of protons increases, since they are confined to a tiny volume and repel each other. The energy of the strong force holding the nucleus together also increases, but at a slower rate, as if inside the nucleus, only nucleons close to each other are tightly bound, not ones more widely separated.^[7]

The net binding energy of a nucleus is that of the nuclear attraction, minus the disruptive energy of the electric force. As nuclei get heavier than helium, their net binding energy per nucleon (deduced from the difference in mass between the nucleus and the sum of masses of component nucleons) grows more and more slowly, reaching its peak at iron. As nucleons are added, the total nuclear binding energy always increases—but the total disruptive energy of electric forces (positive protons repelling other protons) also increases, and past iron, the second increase outweighs the first. Iron-56 (⁵⁶Fe) is the most efficiently bound nucleus^[7] meaning that it has the least average mass per nucleon. However, nickel-62 is the most tightly bound nucleus in terms of energy of binding per nucleon ^[8]. (Nickel-62's higher energy of binding does not translate to a larger mean mass loss than Fe-56, because Ni-62 has a slightly higher ratio of neutrons/protons than does iron-56, and the presence of the heavier neutrons increases nickel-62's average mass per nucleon).

To reduce the disruptive energy, the weak interaction allows the number of neutrons to exceed that of protons—for instance, the main isotope of iron has 26 protons and 30 neutrons. Isotopes also exist where the number of neutrons differs from the most stable number for that number of nucleons. If the ratio of protons to neutrons is too far from stability, nucleons may spontaneously change from proton to neutron, or neutron to proton.

The two methods for this conversion are mediated by the weak force, and involve types of beta decay. In the simplest beta decay, neutrons are converted to protons by emitting a negative electron and an antineutrino. This is always possible outside a nucleus because neutrons are more massive than protons by an equivalent of about 2.5 electrons. In the opposite process, which only happens within a nucleus, and not to free particles, a proton may become a neutron by ejecting a positron. This is permitted if enough energy is available between parent and daughter nuclides to do this (the required energy difference is equal to 1.022 MeV, which is the mass of 2 electrons). If the mass difference between parent and daughter is less than this, a proton-rich nucleus may still convert protons to neutrons by the process of electron capture, in which a proton simply electron captures one of the atom's K orbital electrons, emits a neutrino, and becomes a neutron.^[7]

Among the heaviest nuclei, starting with tellurium nuclei (element 52) containing 106 or more nucleons, electric forces may be so destabilizing that entire chunks of the nucleus may be ejected, usually as alpha particles, which consist of two protons and two neutrons (alpha particles are fast helium nuclei). (Beryllium-8 also decays, very quickly, into two alpha particles.) Alpha particles are extremely stable. This type of decay becomes more and more probable as elements rise in atomic weight past 106.

The curve of binding energy is a graph that plots the binding energy per nucleon against atomic mass. This curve has its main peak at iron and nickel and then slowly decreases again, and also a narrow isolated peak at helium, which as noted is very stable. The heaviest nuclei in nature, uranium ²³⁸U, are unstable, but having a half-life of 4.5 billion years, close to the age of the Earth, they are still relatively abundant; they (and other nuclei heavier than helium) have formed in stellar evolution events like supernova explosions ^[9] preceding the formation of the solar system. The most common isotope of thorium, ²³²Th, also undergoes alpha particle emission, and its half-life (time over which half a number of atoms decays) is even longer, by several times. In each of these, radioactive decay produces daughter isotopes that are also unstable, starting a chain of decays that ends in some stable isotope of lead.^[7]

Determining nuclear binding energy

Calculation can be employed to determine the nuclear binding energy of nuclei. The calculation involves determining the mass defect, converting it into energy, and expressing the result as energy per mole of atoms, or as energy per nucleon.^[2]

Conversion of mass defect into energy

Mass defect is defined as the difference between the mass of a nucleus, and the sum of the masses of the nucleons of which it is composed. The mass defect is determined by calculating three quantities.^[2] These are: the actual mass of the nucleus, the composition of the nucleus (number of protons and of neutrons), and the masses of a proton and of a neutron. This is then followed by converting the mass defect into energy. This quantity is the nuclear binding energy, however it must be expressed as energy per mole of atoms or as energy per nucleon.^[2]

Fission and fusion

Nuclear energy is released by the splitting (fission) or merging (fusion) of the nuclei of atom(s). The conversion of nuclear mass-energy to a form of energy, which can remove some mass when the energy is removed, is consistent with the mass-energy equivalence formula:

ΔE = Δm c²,

in which,

ΔE = energy release,
Δm = mass defect,
and c = the speed of light in a vacuum (a physical constant 299,792,458 m/s by definition).

Nuclear energy was first discovered by French physicist Henri Becquerel in 1896, when he found that photographic plates stored in the dark near uranium were blackened like X-ray plates (X-rays had recently been discovered in 1895).^[10]

Nickel-62 has the highest binding energy per nucleon of any isotope. If an atom of lower average binding energy is changed into two atoms of higher average binding energy, energy is given off. Also, if two atoms of lower average binding energy fuse into an atom of higher average binding energy, energy is given off. The chart shows that fusion of hydrogen, the combination to form heavier atoms, releases energy, as does fission of uranium, the breaking up of a larger nucleus into smaller parts. Stability varies between isotopes: the isotope U-235 is much less stable than the more common U-238.

Nuclear energy is released by three exoenergetic (or exothermic) processes:

• Radioactive decay, where a neutron or proton in the radioactive nucleus decays spontaneously by emitting either particles, electromagnetic radiation (gamma rays), or both. Note that for radioactive decay, it is not strictly necessary for the binding energy to increase. What is strictly necessary is that the mass decrease. If a neutron turns into a proton and the energy of the decay is less than 0.782343 MeV (such as rubidium-87 decaying to strontium-87), the average binding energy per nucleon will actually decrease.
• Fusion, two atomic nuclei fuse together to form a heavier nucleus
• Fission, the breaking of a heavy nucleus into two (or more rarely three) lighter nuclei

Binding energy for atoms

The binding energy of an atom (including its electrons) is not the same as the binding energy of the atom's nucleus. The measured mass deficits of isotopes are always listed as mass deficits of the neutral atoms of that isotope, and mostly in MeV. As a consequence, the listed mass deficits are not a measure for the stability or binding energy of isolated nuclei, but for the whole atoms. This has very practical reasons, because it is very hard to totally ionize heavy elements, i.e. strip them of all of their electrons.

This practice is useful for other reasons, too: stripping all the electrons from a heavy unstable nucleus (thus producing a bare nucleus) changes the lifetime of the nucleus, or the nucleus of a stable neutral atom can likewise become unstable after stripping, indicating that the nucleus cannot be treated independently. Examples of this have been shown in bound-state β decay experiments performed at the GSI) heavy ion accelerator.^{[11] [12]} This is also evident from phenomena like electron capture. Theoretically, in orbital models of heavy atoms, the electron orbits partially inside the nucleus (it does not orbit in a strict sense, but has a non-vanishing probability of being located inside the nucleus).

A nuclear decay happens to the nucleus, meaning that properties ascribed to the nucleus change in the event. In the field of physics the concept of "mass deficit" as a measure for "binding energy" means "mass deficit of the neutral atom" (not just the nucleus) and is a measure for stability of the whole atom.

Nuclear binding energy curve

In the periodic table of elements, the series of light elements
from hydrogen up to sodium is observed to exhibit generally
increasing binding energy per nucleon as the atomic mass
 increases. This increase is generated by increasing forces per
nucleon in the nucleus, as each additional nucleon is attracted
by other nearby nucleons, and thus more tightly bound to
the whole.

The region of increasing binding energy is followed by a region of relative stability (saturation) in the sequence from magnesium through xenon. In this region, the nucleus has become large enough that nuclear forces no longer completely extend efficiently across its width. Attractive nuclear forces in this region, as atomic mass increases, are nearly balanced by repellent electromagnetic forces between protons, as the atomic number increases.

Finally, in elements heavier than xenon, there is a decrease in binding energy per nucleon as atomic number increases. In this region of nuclear size, electromagnetic repulsive forces are beginning to overcome the strong nuclear force attraction.

At the peak of binding energy, nickel-62 is the most tightly bound nucleus (per nucleon), followed by iron-58 and iron-56.^[13] This is the approximate basic reason why iron and nickel are very common metals in planetary cores, since they are produced profusely as end products in supernovae and in the final stages of silicon burning in stars. However, it is not binding energy per defined nucleon (as defined above), which controls which exact nuclei are made, because within stars, neutrons are free to convert to protons to release even more energy, per generic nucleon, if the result is a stable nucleus with a larger fraction of protons. In fact, it has been argued that photodisintegration of ⁶²Ni to form ⁵⁶Fe may be energetically possible in an extremely hot star core, due to this beta decay conversion of neutrons to protons.^[14] The conclusion is that at the pressure and temperature conditions in the cores of large stars, energy is released by converting all matter into ⁵⁶Fe nuclei (ionized atoms). (However, at high temperatures not all matter will be in the lowest energy state.) This energetic maximum should also hold for ambient conditions, say T = 298 K and p = 1 atm, for neutral condensed matter consisting of ⁵⁶Fe atoms—however, in these conditions nuclei of atoms are inhibited from fusing into the most stable and low energy state of matter.

It is generally believed that iron-56 is more common than nickel isotopes in the universe for mechanistic reasons, because its unstable progenitor nickel-56 is copiously made by staged build-up of 14 helium nuclei inside supernovas, where it has no time to decay to iron before being released into the interstellar medium in a matter of a few minutes, as the supernova explodes. However, nickel-56 then decays to cobalt-56 within a few weeks, then this radioisotope finally decays to iron-56 with a half life of about 77.3 days. The radioactive decay-powered light curve of such a process has been observed to happen in type II supernovae, such as SN 1987A. In a star, there are no good ways to create nickel-62 by alpha-addition processes, or else there would presumably be more of this highly stable nuclide in the universe.

Binding energy and nuclide masses

The fact that the maximum binding energy is found in medium-sized nuclei is a consequence of the trade-off in the effects of two opposing forces that have different range characteristics. The attractive nuclear force (strong nuclear force), which binds protons and neutrons equally to each other, has a limited range due to a rapid exponential decrease in this force with distance. However, the repelling electromagnetic force, which acts between protons to force nuclei apart, falls off with distance much more slowly (as the inverse square of distance). For nuclei larger than about four nucleons in diameter, the additional repelling force of additional protons more than offsets any binding energy that results between further added nucleons as a result of additional strong force interactions. Such nuclei become increasingly less tightly bound as their size increases, though most of them are still stable. Finally, nuclei containing more than 209 nucleons (larger than about 6 nucleons in diameter) are all too large to be stable, and are subject to spontaneous decay to smaller nuclei.

Nuclear fusion produces energy by combining the very lightest elements into more tightly bound elements (such as hydrogen into helium), and nuclear fission produces energy by splitting the heaviest elements (such as uranium and plutonium) into more tightly bound elements (such as barium and krypton). Both processes produce energy, because middle-sized nuclei are the most tightly bound of all.

As seen above in the example of deuterium, nuclear binding energies are large enough that they may be easily measured as fractional mass deficits, according to the equivalence of mass and energy. The atomic binding energy is simply the amount of energy (and mass) released, when a collection of free nucleons are joined together to form a nucleus.

Nuclear binding energy can be computed from the difference in mass of a nucleus, and the sum of the masses of the number of free neutrons and protons that make up the nucleus. Once this mass difference, called the mass defect or mass deficiency, is known, Einstein's mass-energy equivalence formula E = mc² can be used to compute the binding energy of any nucleus. Early nuclear physicists used to refer to computing this value as a "packing fraction" calculation.

For example, the atomic mass unit (1 u) is defined as 1/12 of the mass of a ¹²C atom—but the atomic mass of a ¹H atom (which is a proton plus electron) is 1.007825 u, so each nucleon in ¹²C has lost, on average, about 0.8% of its mass in the form of binding energy.

Semiempirical formula for nuclear binding energy

For a nucleus with A nucleons, including Z protons and N neutrons, a semi-empirical formula for the binding energy (BE) per nucleon is:

${\displaystyle {\frac {\text{BE}}{A\cdot {\text{MeV}}}}=a-{\frac {b}{A^{1/3}}}-{\frac {cZ^{2}}{A^{4/3}}}-{\frac {d\left(N-Z\right)^{2}}{A^{2}}}\pm {\frac {e}{A^{7/4}}}}$

where the coefficients are given by: ${\displaystyle a=14.0}$; ${\displaystyle b=13.0}$; ${\displaystyle c=0.585}$; ${\displaystyle d=19.3}$; ${\displaystyle e=33}$.

The first term ${\displaystyle a}$ is called the saturation contribution and ensures that the binding energy per nucleon is the same for all nuclei to a first approximation. The term ${\displaystyle -b/A^{1/3}}$ is a surface tension effect and is proportional to the number of nucleons that are situated on the nuclear surface; it is largest for light nuclei. The term ${\displaystyle -cZ^{2}/A^{4/3}}$ is the Coulomb electrostatic repulsion; this becomes more important as ${\displaystyle Z}$ increases. The symmetry correction term ${\displaystyle -d(N-Z)^{2}/A^{2}}$ takes into account the fact that in the absence of other effects the most stable arrangement has equal numbers of protons and neutrons; this is because the n-p interaction in a nucleus is stronger than either the n-n or p-p interaction. The pairing term ${\displaystyle \pm e/A^{7/4}}$ is purely empirical; it is + for even-even nuclei and - for odd-odd nuclei.

A graphical representation of the semi-empirical binding

energy formula. The binding energy per nucleon in MeV

(highest numbers in yellow, in excess of 8.5 MeV per

nucleon) is plotted for various nuclides as a function of

Z, the atomic number (y-axis), vs. N, the number of

neutrons (x-axis). The highest numbers are seen for

Z = 26 (iron).

Glueball

From Wikipedia, the free encyclopedia

In particle physics, a glueball (also gluonium, gluon-ball) is a hypothetical composite particle.^[1] It consists solely of gluon particles, without valence quarks. Such a state is possible because gluons carry color charge and experience the strong interaction between themselves. Glueballs are extremely difficult to identify in particle accelerators, because they mix with ordinary meson states.^[2]

Theoretical calculations show that glueballs should exist at energy ranges accessible with current collider technology. However, due to the aforementioned difficulty (among others), they have so far not been observed and identified with certainty,^[3] although phenomenological calculations have suggested that an experimentally identified glueball candidate, denoted ${\displaystyle f_{0}(1710)}$, has properties consistent with those expected of a Standard Model glueball.^[4]

The prediction that glueballs exist is one of the most important predictions of the Standard Model of particle physics that has not yet been confirmed experimentally.^[5] Glueballs are the only particles predicted by the Standard Model with total angular momentum (J) (sometimes called "intrinsic spin") that could be either 2 or 3 in their ground states.

Properties of glueballs

In principle, it is theoretically possible for all properties of glueballs to be calculated exactly and derived directly from the equations and fundamental physical constants of quantum chromodynamics (QCD) without further experimental input. So, the predicted properties of these hypothetical particles can be described in exquisite detail using only Standard Model physics which have wide acceptance in the theoretical physics literature. But, there is considerable uncertainty in the measurement of some of the relevant key physical constants, and the QCD calculations are so difficult that solutions to these equations are almost always numerical approximations (reached by several very different methodologies). This can lead to variation in theoretical predictions of glueball properties like mass and branching ratios in glueball decays.

Constituent particles and color charge

Theoretical studies of glueballs have focused on glueballs consisting of either two gluons or three gluons, by analogy to mesons and baryons that have two and three quarks respectively. As in the case of mesons and baryons, glueballs would be QCD color charge neutral. The baryon number of a glueball is zero.

Total angular momentum

Two gluon glueballs can have total angular momentum (J) of 0 (which are scalar or pseudo-scalar) or 2 (tensor). Three gluon glueballs can have total angular momentum (J) of 1 (vector boson) or 3. All glueballs have integer total angular momentum which implies that they are bosons rather than fermions.

Glueballs are the only particles predicted by the Standard Model with total angular momentum (J) (sometimes called "intrinsic spin") that could be either 2 or 3 in their ground states, although mesons made of two quarks with J=0 and J=1 with similar masses have been observed and excited states of other mesons can have these values of total angular momentum.

Fundamental particles with ground states having J=0 or J=2 are easily distinguished from glueballs. The hypothetical graviton, while having a total angular momentum J=2 would be massless and lack color charge, and so would be easily distinguished from glueballs. The Standard Model Higgs boson for which an experimentally measured mass of about 125–126 GeV/c² has been determined is the only fundamental particle with J=0 in the Standard Model. It also lacks color charge and hence does not engage in strong force interactions. But the Higgs boson is about 25–80 times as heavy as the mass of the various glueball states predicted by the Standard Model.

Electric charge

All glueballs would have an electric charge of zero as gluons themselves do not have an electric charge.

Mass and parity

Glueballs are predicted by quantum chromodynamics to be massive, notwithstanding the fact that gluons themselves have zero rest mass in the Standard Model. Glueballs with all four possible combinations of quantum numbers P (parity) and C (c-parity) for every possible total angular momentum have been considered, producing at least fifteen possible glueball states including excited glueball states that share the same quantum numbers but have differing masses with the lightest states having masses as low as 1.4 GeV/c² (for a glueball with quantum numbers J=0, P=+, C=+), and the heaviest states having masses as great as almost 5 GeV/c² (for a glueball with quantum numbers J=0, P=+, C=-).^[6]

These masses are on the same order of magnitude as the masses of many experimentally observed mesons and baryons, as well as to the masses of the tau lepton, charm quark, bottom quark, some hydrogen isotopes, and some helium isotopes.

Stability and decay channels

Just as all Standard Model mesons and baryons, except the proton, are unstable in isolation, all glueballs are predicted by the Standard Model to be unstable in isolation, with various QCD calculations predicting the total decay width (which is functionally related to half-life) for various glueball states. QCD calculations also make predictions regarding the expected decay patterns of glueballs.^[7][8] For example, glueballs would not have radiative or two photon decays, but would have decays into pairs of pions, pairs of kaons, or pairs of eta mesons.^[7]

Practical impact on macroscopic low energy physics

Feynman diagram of a glueball (G) decaying to two pions (
π
). Such decays help the study of and search for glueballs.^[9]

Because Standard Model glueballs are so ephemeral (decaying almost immediately into more stable decay products) and are only generated in high energy physics, glueballs only arise synthetically in the natural conditions found on Earth that humans can easily observe. They are scientifically notable mostly because they are a testable prediction of the Standard Model, and not because of phenomenological impact on macroscopic processes, or their engineering applications.

Lattice QCD simulations

Lattice QCD provides a way to study the glueball spectrum theoretically and from first principles. Some of the first quantities calculated using lattice QCD methods (in 1980) were glueball mass estimates.^[10] Morningstar and Peardon^[11] computed in 1999 the masses of the lightest glueballs in QCD without dynamical quarks. The three lowest states are tabulated below. The presence of dynamical quarks would slightly alter these data, but also makes the computations more difficult. Since that time calculations within QCD (lattice and sum rules) find the lightest glueball to be a scalar with mass in the range of about 1000–1700 MeV.^[12]

J P'C	mass
0++	1730 ±80 MeV
2++	2400 ±120 MeV
0−+	2590 ±130 MeV

Experimental candidates

Particle accelerator experiments are often able to identify unstable composite particles and assign masses to those particles to a precision of approximately 10 MeV/c², without being able to immediately assign to the particle resonance that is observed all of the properties of that particle. Scores of such particles have been detected, although particles detected in some experiments but not others can be viewed as doubtful. Some of the candidate particle resonances that could be glueballs, although the evidence is not definitive, include the following:

Vector, Pseudo-Vector, or Tensor Glueball Candidates:

• X(3020) observed by the BaBar collaboration is a candidate for an excited state of the 2−+, 1+− or 1−− glueball states with a mass of about 3.02 GeV/c².^[5]

Scalar Glueball Candidates:

• f₀(500) also known as σ – the properties of this particle are possibly consistent with a 1000 MeV or 1500 MeV mass glueball.^[13]
• f₀(980) – the structure of this composite particle is consistent with the existence of a light glueball.^[13]
• f₀(1370) – existence of this resonance is disputed but is a candidate for a glueball-meson mixing state^[13]
• f₀(1500) – existence of this resonance is undisputed but its status as a glueball-meson mixing state or pure glueball is not well established.^[13]
• f₀(1710) – existence of this resonance is undisputed but its status as a glueball-meson mixing state or pure glueball is not well established.^[13]

Other Glueball Candidates:

• Gluon jets at the LEP experiment show a 40% excess over theoretical expectations of electromagnetically neutral clusters which suggests that electromagnetically neutral particles expected in gluon rich environments such as glueballs are likely to be present.^[13]

Many of these candidates have been the subject of active investigation for at least eighteen years.^[7] The GlueX experiment has been specifically designed to produce more definitive experimental evidence of glueballs.^[14]