Manifold

From Wikipedia, the free encyclopedia

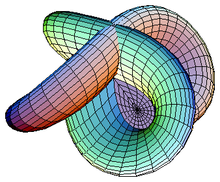
The real projective plane is a two-dimensional manifold that cannot be realized in three dimensions without self-intersection, shown here as Boy's surface.

The surface of the Earth requires (at least) two charts to include every point. Here the globe is decomposed into charts around the North and South Poles.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, each point of an n-dimensional manifold has a neighbourhood that is homeomorphic to the Euclidean space of dimension n. In this more precise terminology, a manifold is referred to as an n-manifold.

One-dimensional manifolds include lines and circles, but not figure eights (because they have crossing points that are not locally homeomorphic to Euclidean 1-space). Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, which can all be embedded (formed without self-intersections) in three dimensional real space, but also the Klein bottle and real projective plane, which will always self-intersect when immersed in three-dimensional real space.

Although a manifold locally resembles Euclidean space, meaning that every point has a neighborhood homeomorphic to an open subset of Euclidean space, globally it may not: manifolds in general are not homeomorphic to Euclidean space. For example, the surface of the sphere is not homeomorphic to the Euclidean plane, because (among other properties) it has the global topological property of compactness that Euclidean space lacks, but in a region it can be charted by means of map projections of the region into the Euclidean plane (in the context of manifolds they are called charts). When a region appears in two neighbouring charts, the two representations do not coincide exactly and a transformation is needed to pass from one to the other, called a transition map.

The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described and understood in terms of the simpler local topological properties of Euclidean space. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions.

Manifolds can be equipped with additional structure. One important class of manifolds is the class of differentiable manifolds; this differentiable structure allows calculus to be done on manifolds. A Riemannian metric on a manifold allows distances and angles to be measured. Symplectic manifolds serve as the phase spaces in the Hamiltonian formalism of classical mechanics, while four-dimensional Lorentzian manifolds model spacetime in general relativity.

Motivating examples

A surface is a two dimensional manifold, meaning that it locally resembles the Euclidean plane near each point. For example, the surface of a globe can be described by a collection of maps (called charts), which together form an atlas of the globe. Although no individual map is sufficient to cover the entire surface of the globe, any place in the globe will be in at least one of the charts.

Many places will appear in more than one chart. For example, a map of North America will likely include parts of South America and the Arctic circle. These regions of the globe will be described in full in separate charts, which in turn will contain parts of North America. There is a relation between adjacent charts, called a transition map that allows them to be consistently patched together to cover the whole of the globe.

Describing the coordinate charts on surfaces explicitly requires knowledge of functions of two variables, because these patching functions must map a region in the plane to another region of the plane. However, one-dimensional examples of manifolds (or curves) can be described with functions of a single variable only.

Manifolds have good applications in computer-graphics and augmented-reality given the need to associate pictures(texture) to coordinates (i.e CT scans ) . In augmentet reality setting, a picture (tangent plane) can be seen as something associated with a coordinate and by using sensors for detecting movements and rotation one can have knowledge of how the picture is orienteted and placed in space.

Circle

Figure 1: The four charts each map part of the circle to an open interval, and together cover the whole circle.

After a line, the circle is the simplest example of a topological manifold. Topology ignores bending, so a small piece of a circle is treated exactly the same as a small piece of a line. Consider, for instance, the top part of the unit circle, x² + y² = 1, where the y-coordinate is positive (indicated by the yellow circular arc in Figure 1). Any point of this arc can be uniquely described by its x-coordinate. So, projection onto the first coordinate is a continuous, and invertible, mapping from the upper arc to the open interval (−1, 1):

${\displaystyle \chi _{\mathrm {top} }(x,y)=x.\,}$

Such functions along with the open regions they map are called charts. Similarly, there are charts for the bottom (red), left (blue), and right (green) parts of the circle:

${\displaystyle {\begin{aligned}\chi _{\mathrm {bottom} }(x,y)&=x\\\chi _{\mathrm {left} }(x,y)&=y\\\chi _{\mathrm {right} }(x,y)&=y.\end{aligned}}}$

Together, these parts cover the whole circle and the four charts form an atlas for the circle.

The top and right charts, ${\displaystyle \chi _{\mathrm {top} }}$ and ${\displaystyle \chi _{\mathrm {right} }}$ respectively, overlap in their domain: their intersection lies in the quarter of the circle where both the ${\displaystyle x}$- and the ${\displaystyle y}$-coordinates are positive. Each map this part into the interval ${\displaystyle (0,1)}$, though differently. Thus a function ${\displaystyle T:(0,1)\rightarrow (0,1)=\chi _{\mathrm {right} }\circ \chi _{\mathrm {top} }^{-1}}$ can be constructed, which takes values from the co-domain of ${\displaystyle \chi _{\mathrm {top} }}$ back to the circle using the inverse, followed by the ${\displaystyle \chi _{\mathrm {right} }}$ back to the interval. Let a be any number in ${\displaystyle (0,1)}$, then:

${\displaystyle {\begin{aligned}T(a)&=\chi _{\mathrm {right} }\left(\chi _{\mathrm {top} }^{-1}\left[a\right]\right)\\&=\chi _{\mathrm {right} }\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^{2}}}\end{aligned}}}$

Such a function is called a transition map.

Figure 2: A circle manifold chart based on slope, covering all but one point of the circle.

The top, bottom, left, and right charts show that the circle is a manifold, but they do not form the only possible atlas. Charts need not be geometric projections, and the number of charts is a matter of choice. Consider the charts

${\displaystyle \chi _{\mathrm {minus} }(x,y)=s={\frac {y}{1+x}}}$

and

${\displaystyle \chi _{\mathrm {plus} }(x,y)=t={\frac {y}{1-x}}}$

Here s is the slope of the line through the point at coordinates (x,y) and the fixed pivot point (−1, 0); t follows similarly, but with pivot point (+1, 0). The inverse mapping from s to (x, y) is given by

${\displaystyle {\begin{aligned}x&={\frac {1-s^{2}}{1+s^{2}}}\\y&={\frac {2s}{1+s^{2}}}\end{aligned}}}$

It can easily be confirmed that x² + y² = 1 for all values of the slope s. These two charts provide a second atlas for the circle, with

${\displaystyle t={\frac {1}{s}}}$

Each chart omits a single point, either (−1, 0) for s or (+1, 0) for t, so neither chart alone is sufficient to cover the whole circle. It can be proved that it is not possible to cover the full circle with a single chart. For example, although it is possible to construct a circle from a single line interval by overlapping and "gluing" the ends, this does not produce a chart; a portion of the circle will be mapped to both ends at once, losing invertibility.

Sphere

The sphere is an example of a surface. The unit sphere of implicit equation

x² + y² + z² – 1 = 0

may be covered by an atlas of six charts: the plane z = 0 divides the sphere into two half spheres (z > 0 and z < 0), which may both be mapped on the disc x² + y² > 1 by the projection on the xy plane of coordinates. This provides two charts; the four other charts are provided by a similar construction with the two other coordinate planes.

As for the circle, one may define one chart that covers the whole sphere excluding one point. Thus two charts are sufficient, but the sphere cannot be covered by a single chart.

This example is historically significant, as it has motivated the terminology; it became apparent that the whole surface of the Earth cannot have a plane representation consisting of a single map (also called "chart", see nautical chart), and therefore one needs atlases for covering the whole Earth surface.

Enriched circle

Viewed using calculus, the circle transition function T is simply a function between open intervals, which gives a meaning to the statement that T is differentiable. The transition map T, and all the others, are differentiable on (0, 1); therefore, with this atlas the circle is a differentiable manifold. It is also smooth and analytic because the transition functions have these properties as well.

Other circle properties allow it to meet the requirements of more specialized types of manifold. For example, the circle has a notion of distance between two points, the arc-length between the points; hence it is a Riemannian manifold.

Other curves

Four manifolds from algebraic curves: ■ circles, ■ parabola, ■ hyperbola, ■ cubic.

Manifolds need not be connected (all in "one piece"); an example is a pair of separate circles.

Manifolds need not be closed; thus a line segment without its end points is a manifold. And they are never countable, unless the dimension of the manifold is 0. Putting these freedoms together, other examples of manifolds are a parabola, a hyperbola (two open, infinite pieces), and the locus of points on a cubic curve y² = x³ − x (a closed loop piece and an open, infinite piece).

However, excluded are examples like two touching circles that share a point to form a figure-8; at the shared point a satisfactory chart cannot be created. Even with the bending allowed by topology, the vicinity of the shared point looks like a "+", not a line. A "+" is not homeomorphic to a closed interval (line segment), since deleting the center point from the "+" gives a space with four components (i.e. pieces), whereas deleting a point from a closed interval gives a space with at most two pieces; topological operations always preserve the number of pieces.

Mathematical definition

Informally, a manifold is a space that is "modeled on" Euclidean space.

There are many different kinds of manifolds, depending on the context. In geometry and topology, all manifolds are topological manifolds, possibly with additional structure, such as a differentiable structure. A manifold can be constructed by giving a collection of coordinate charts, that is a covering by open sets with homeomorphisms to a Euclidean space, and patching functions: homeomorphisms from one region of Euclidean space to another region if they correspond to the same part of the manifold in two different coordinate charts. A manifold can be given additional structure if the patching functions satisfy axioms beyond continuity. For instance, differentiable manifolds have homeomorphisms on overlapping neighborhoods diffeomorphic with each other, so that the manifold has a well-defined set of functions which are differentiable in each neighborhood, and so differentiable on the manifold as a whole.

Formally, a (topological) manifold is a second countable Hausdorff space that is locally homeomorphic to Euclidean space.

Second countable and Hausdorff are point-set conditions; second countable excludes spaces which are in some sense 'too large' such as the long line, while Hausdorff excludes spaces such as "the line with two origins" (these generalizations of manifolds are discussed in non-Hausdorff manifolds).

Locally homeomorphic to Euclidean space means that every point has a neighborhood homeomorphic to an open Euclidean n-ball,

${\displaystyle \mathbf {B} ^{n}=\left\{(x_{1},x_{2},\dots ,x_{n})\in \mathbb {R} ^{n}\mid x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}<1 annotation="" right="">$

More precisely, locally homeomorphic here means that each point m in the manifold M has an open neighborhood homeomorphic to an open neighborhood in Euclidean space, not to the unit ball specifically. However, given such a homeomorphism, the pre-image of an ${\displaystyle \epsilon }$-ball gives a homeomorphism between the unit ball and a smaller neighborhood of m, so this is no loss of generality. For topological or differentiable manifolds, one can also ask that every point have a neighborhood homeomorphic to all of Euclidean space (as this is diffeomorphic to the unit ball), but this cannot be done for complex manifolds, as the complex unit ball is not holomorphic to complex space.

Generally manifolds are taken to have a fixed dimension (the space must be locally homeomorphic to a fixed n-ball), and such a space is called an n-manifold; however, some authors admit manifolds where different points can have different dimensions.^[1] If a manifold has a fixed dimension, it is called a pure manifold. For example, the sphere has a constant dimension of 2 and is therefore a pure manifold whereas the disjoint union of a sphere and a line in three-dimensional space is not a pure manifold. Since dimension is a local invariant (i.e. the map sending each point to the dimension of its neighbourhood over which a chart is defined, is locally constant), each connected component has a fixed dimension.

Scheme-theoretically, a manifold is a locally ringed space, whose structure sheaf is locally isomorphic to the sheaf of continuous (or differentiable, or complex-analytic, etc.) functions on Euclidean space. This definition is mostly used when discussing analytic manifolds in algebraic geometry.

Charts, atlases, and transition maps

The spherical Earth is navigated using flat maps or charts, collected in an atlas. Similarly, a differentiable manifold can be described using mathematical maps, called coordinate charts, collected in a mathematical atlas. It is not generally possible to describe a manifold with just one chart, because the global structure of the manifold is different from the simple structure of the charts. For example, no single flat map can represent the entire Earth without separation of adjacent features across the map's boundaries or duplication of coverage. When a manifold is constructed from multiple overlapping charts, the regions where they overlap carry information essential to understanding the global structure.

Charts

A coordinate map, a coordinate chart, or simply a chart, of a manifold is an invertible map between a subset of the manifold and a simple space such that both the map and its inverse preserve the desired structure.^[2] For a topological manifold, the simple space is a subset of some Euclidean space Rⁿ and interest focuses on the topological structure. This structure is preserved by homeomorphisms, invertible maps that are continuous in both directions.

In the case of a differentiable manifold, a set of charts called an atlas allows us to do calculus on manifolds. Polar coordinates, for example, form a chart for the plane R² minus the positive x-axis and the origin. Another example of a chart is the map χ_top mentioned in the section above, a chart for the circle.

Atlases

The description of most manifolds requires more than one chart (a single chart is adequate for only the simplest manifolds). A specific collection of charts which covers a manifold is called an atlas. An atlas is not unique as all manifolds can be covered multiple ways using different combinations of charts. Two atlases are said to be equivalent if their union is also an atlas.

The atlas containing all possible charts consistent with a given atlas is called the maximal atlas (i.e. an equivalence class containing that given atlas (under the already defined equivalence relation given in the previous paragraph)). Unlike an ordinary atlas, the maximal atlas of a given manifold is unique. Though it is useful for definitions, it is an abstract object and not used directly (e.g. in calculations).

Transition maps

Charts in an atlas may overlap and a single point of a manifold may be represented in several charts. If two charts overlap, parts of them represent the same region of the manifold, just as a map of Europe and a map of Asia may both contain Moscow. Given two overlapping charts, a transition function can be defined which goes from an open ball in Rⁿ to the manifold and then back to another (or perhaps the same) open ball in Rⁿ. The resultant map, like the map T in the circle example above, is called a change of coordinates, a coordinate transformation, a transition function, or a transition map.

Additional structure

An atlas can also be used to define additional structure on the manifold. The structure is first defined on each chart separately. If all the transition maps are compatible with this structure, the structure transfers to the manifold.

This is the standard way differentiable manifolds are defined. If the transition functions of an atlas for a topological manifold preserve the natural differential structure of Rⁿ (that is, if they are diffeomorphisms), the differential structure transfers to the manifold and turns it into a differentiable manifold. Complex manifolds are introduced in an analogous way by requiring that the transition functions of an atlas are holomorphic functions. For symplectic manifolds, the transition functions must be symplectomorphisms.

The structure on the manifold depends on the atlas, but sometimes different atlases can be said to give rise to the same structure. Such atlases are called compatible.

These notions are made precise in general through the use of pseudogroups.

Manifold with boundary

A manifold with boundary is a manifold with an edge. For example, a sheet of paper is a 2-manifold with a 1-dimensional boundary. The boundary of an n-manifold with boundary is an (n − 1)-manifold. A disk (circle plus interior) is a 2-manifold with boundary. Its boundary is a circle, a 1-manifold. A square with interior is also a 2-manifold with boundary. A ball (sphere plus interior) is a 3-manifold with boundary. Its boundary is a sphere, a 2-manifold.).

In technical language, a manifold with boundary is a space containing both interior points and boundary points. Every interior point has a neighborhood homeomorphic to the open n-ball {(x₁, x₂, …, x_n) | Σx_i² < 1} . Every boundary point has a neighborhood homeomorphic to the "half" n-ball {(x₁, x₂, …, x_n) | Σx_i² < 1 and x₁ ≥ 0} . The homeomorphism must send each boundary point to a point with x₁ = 0.

Boundary and interior

Let M be a manifold with boundary. The interior of M, denoted Int M, is the set of points in M which have neighborhoods homeomorphic to an open subset of Rⁿ. The boundary of M, denoted ∂M, is the complement of Int M in M. The boundary points can be characterized as those points which land on the boundary hyperplane (x_n = 0) of Rⁿ₊ under some coordinate chart.

If M is a manifold with boundary of dimension n, then Int M is a manifold (without boundary) of dimension n and ∂M is a manifold (without boundary) of dimension n − 1.

Construction

A single manifold can be constructed in different ways, each stressing a different aspect of the manifold, thereby leading to a slightly different viewpoint.

Charts

The chart maps the part of the sphere with positive z coordinate to a disc.

Perhaps the simplest way to construct a manifold is the one used in the example above of the circle. First, a subset of R² is identified, and then an atlas covering this subset is constructed. The concept of manifold grew historically from constructions like this. Here is another example, applying this method to the construction of a sphere:

Sphere with charts

A sphere can be treated in almost the same way as the circle. In mathematics a sphere is just the surface (not the solid interior), which can be defined as a subset of R³:

${\displaystyle S=\left\{(x,y,z)\in \mathbf {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}.}$

The sphere is two-dimensional, so each chart will map part of the sphere to an open subset of R². Consider the northern hemisphere, which is the part with positive z coordinate (coloured red in the picture on the right). The function χ defined by

${\displaystyle \chi (x,y,z)=(x,y),\ }$

maps the northern hemisphere to the open unit disc by projecting it on the (x, y) plane. A similar chart exists for the southern hemisphere. Together with two charts projecting on the (x, z) plane and two charts projecting on the (y, z) plane, an atlas of six charts is obtained which covers the entire sphere.

This can be easily generalized to higher-dimensional spheres.

Patchwork

A manifold can be constructed by gluing together pieces in a consistent manner, making them into overlapping charts. This construction is possible for any manifold and hence it is often used as a characterisation, especially for differentiable and Riemannian manifolds. It focuses on an atlas, as the patches naturally provide charts, and since there is no exterior space involved it leads to an intrinsic view of the manifold.

The manifold is constructed by specifying an atlas, which is itself defined by transition maps. A point of the manifold is therefore an equivalence class of points which are mapped to each other by transition maps. Charts map equivalence classes to points of a single patch. There are usually strong demands on the consistency of the transition maps. For topological manifolds they are required to be homeomorphisms; if they are also diffeomorphisms, the resulting manifold is a differentiable manifold.

This can be illustrated with the transition map t = ¹⁄_s from the second half of the circle example. Start with two copies of the line. Use the coordinate s for the first copy, and t for the second copy. Now, glue both copies together by identifying the point t on the second copy with the point s = ¹⁄_t on the first copy (the points t = 0 and s = 0 are not identified with any point on the first and second copy, respectively). This gives a circle.

Intrinsic and extrinsic view

The first construction and this construction are very similar, but they represent rather different points of view. In the first construction, the manifold is seen as embedded in some Euclidean space. This is the extrinsic view. When a manifold is viewed in this way, it is easy to use intuition from Euclidean spaces to define additional structure. For example, in a Euclidean space it is always clear whether a vector at some point is tangential or normal to some surface through that point.

The patchwork construction does not use any embedding, but simply views the manifold as a topological space by itself. This abstract point of view is called the intrinsic view. It can make it harder to imagine what a tangent vector might be, and there is no intrinsic notion of a normal bundle, but instead there is an intrinsic stable normal bundle.

n-Sphere as a patchwork

The n-sphere Sⁿ is a generalisation of the idea of a circle (1-sphere) and sphere (2-sphere) to higher dimensions. An n-sphere Sⁿ can be constructed by gluing together two copies of Rⁿ. The transition map between them is defined as

${\displaystyle \mathbf {R} ^{n}\setminus \{0\}\to \mathbf {R} ^{n}\setminus \{0\}:x\mapsto x/\|x\|^{2}.}$

This function is its own inverse and thus can be used in both directions. As the transition map is a smooth function, this atlas defines a smooth manifold. In the case n = 1, the example simplifies to the circle example given earlier.

Identifying points of a manifold

It is possible to define different points of a manifold to be same. This can be visualized as gluing these points together in a single point, forming a quotient space. There is, however, no reason to expect such quotient spaces to be manifolds. Among the possible quotient spaces that are not necessarily manifolds, orbifolds and CW complexes are considered to be relatively well-behaved. An example of a quotient space of a manifold that is also a manifold is the real projective space identified as a quotient space of the corresponding sphere.

One method of identifying points (gluing them together) is through a right (or left) action of a group, which acts on the manifold. Two points are identified if one is moved onto the other by some group element. If M is the manifold and G is the group, the resulting quotient space is denoted by M / G (or G \ M).

Manifolds which can be constructed by identifying points include tori and real projective spaces (starting with a plane and a sphere, respectively).

Gluing along boundaries

Two manifolds with boundaries can be glued together along a boundary. If this is done the right way, the result is also a manifold. Similarly, two boundaries of a single manifold can be glued together.

Formally, the gluing is defined by a bijection between the two boundaries^{[dubious – discuss]}. Two points are identified when they are mapped onto each other. For a topological manifold this bijection should be a homeomorphism, otherwise the result will not be a topological manifold. Similarly for a differentiable manifold it has to be a diffeomorphism. For other manifolds other structures should be preserved.

A finite cylinder may be constructed as a manifold by starting with a strip [0, 1] × [0, 1] and gluing a pair of opposite edges on the boundary by a suitable diffeomorphism. A projective plane may be obtained by gluing a sphere with a hole in it to a Möbius strip along their respective circular boundaries.

Cartesian products

The Cartesian product of manifolds is also a manifold.

The dimension of the product manifold is the sum of the dimensions of its factors. Its topology is the product topology, and a Cartesian product of charts is a chart for the product manifold. Thus, an atlas for the product manifold can be constructed using atlases for its factors. If these atlases define a differential structure on the factors, the corresponding atlas defines a differential structure on the product manifold. The same is true for any other structure defined on the factors. If one of the factors has a boundary, the product manifold also has a boundary. Cartesian products may be used to construct tori and finite cylinders, for example, as S¹ × S¹ and S¹ × [0, 1], respectively.

A finite cylinder is a manifold with boundary.

History

The study of manifolds combines many important areas of mathematics: it generalizes concepts such as curves and surfaces as well as ideas from linear algebra and topology.

Early development

Before the modern concept of a manifold there were several important results.

Non-Euclidean geometry considers spaces where Euclid's parallel postulate fails. Saccheri first studied such geometries in 1733 but sought only to disprove them. Gauss, Bolyai and Lobachevsky independently discovered them 100 years later. Their research uncovered two types of spaces whose geometric structures differ from that of classical Euclidean space; these gave rise to hyperbolic geometry and elliptic geometry. In the modern theory of manifolds, these notions correspond to Riemannian manifolds with constant negative and positive curvature, respectively.

Carl Friedrich Gauss may have been the first to consider abstract spaces as mathematical objects in their own right. His theorema egregium gives a method for computing the curvature of a surface without considering the ambient space in which the surface lies. Such a surface would, in modern terminology, be called a manifold; and in modern terms, the theorem proved that the curvature of the surface is an intrinsic property. Manifold theory has come to focus exclusively on these intrinsic properties (or invariants), while largely ignoring the extrinsic properties of the ambient space.

Another, more topological example of an intrinsic property of a manifold is its Euler characteristic. Leonhard Euler showed that for a convex polytope in the three-dimensional Euclidean space with V vertices (or corners), E edges, and F faces,

${\displaystyle V-E+F=2.\ }$

The same formula will hold if we project the vertices and edges of the polytope onto a sphere, creating a topological map with V vertices, E edges, and F faces, and in fact, will remain true for any spherical map, even if it does not arise from any convex polytope.^[3] Thus 2 is a topological invariant of the sphere, called its Euler characteristic. On the other hand, a torus can be sliced open by its 'parallel' and 'meridian' circles, creating a map with V = 1 vertex, E = 2 edges, and F = 1 face. Thus the Euler characteristic of the torus is 1 − 2 + 1 = 0. The Euler characteristic of other surfaces is a useful topological invariant, which can be extended to higher dimensions using Betti numbers. In the mid nineteenth century, the Gauss–Bonnet theorem linked the Euler characteristic to the Gaussian curvature.

Synthesis

Investigations of Niels Henrik Abel and Carl Gustav Jacobi on inversion of elliptic integrals in the first half of 19th century led them to consider special types of complex manifolds, now known as Jacobians. Bernhard Riemann further contributed to their theory, clarifying the geometric meaning of the process of analytic continuation of functions of complex variables.

Another important source of manifolds in 19th century mathematics was analytical mechanics, as developed by Siméon Poisson, Jacobi, and William Rowan Hamilton. The possible states of a mechanical system are thought to be points of an abstract space, phase space in Lagrangian and Hamiltonian formalisms of classical mechanics. This space is, in fact, a high-dimensional manifold, whose dimension corresponds to the degrees of freedom of the system and where the points are specified by their generalized coordinates. For an unconstrained movement of free particles the manifold is equivalent to the Euclidean space, but various conservation laws constrain it to more complicated formations, e.g. Liouville tori. The theory of a rotating solid body, developed in the 18th century by Leonhard Euler and Joseph-Louis Lagrange, gives another example where the manifold is nontrivial. Geometrical and topological aspects of classical mechanics were emphasized by Henri Poincaré, one of the founders of topology.

Riemann was the first one to do extensive work generalizing the idea of a surface to higher dimensions. The name manifold comes from Riemann's original German term, Mannigfaltigkeit, which William Kingdon Clifford translated as "manifoldness". In his Göttingen inaugural lecture, Riemann described the set of all possible values of a variable with certain constraints as a Mannigfaltigkeit, because the variable can have many values. He distinguishes between stetige Mannigfaltigkeit and diskrete Mannigfaltigkeit (continuous manifoldness and discontinuous manifoldness), depending on whether the value changes continuously or not. As continuous examples, Riemann refers to not only colors and the locations of objects in space, but also the possible shapes of a spatial figure. Using induction, Riemann constructs an n-fach ausgedehnte Mannigfaltigkeit (n times extended manifoldness or n-dimensional manifoldness) as a continuous stack of (n−1) dimensional manifoldnesses. Riemann's intuitive notion of a Mannigfaltigkeit evolved into what is today formalized as a manifold. Riemannian manifolds and Riemann surfaces are named after Riemann.

Poincaré's definition

In his very influential paper, Analysis Situs,^[4] Henri Poincaré gave a definition of a (differentiable) manifold (variété) which served as a precursor to the modern concept of a manifold.^[5]

In the first section of Analysis Situs, Poincaré defines a manifold as the level set of a continuously differentiable function between Euclidean spaces that satisfies the nondegeneracy hypothesis of the implicit function theorem. In the third section, he begins by remarking that the graph of a continuously differentiable function is a manifold in the latter sense. He then proposes a new, more general, definition of manifold based on a 'chain of manifolds' (une chaîne des variétés).

Poincaré's notion of a chain of manifolds is a precursor to the modern notion of atlas. In particular, he considers two manifolds defined respectively as graphs of functions ${\displaystyle \theta (y)}$ and ${\displaystyle \theta '\left(y'\right)}$. If these manifolds overlap (a une partie commune), then he requires that the coordinates ${\displaystyle y}$ depend continuously differentiably on the coordinates ${\displaystyle y'}$ and vice versa ('...les ${\displaystyle y}$ sont fonctions analytiques des ${\displaystyle y'}$ et inversement'). In this way he introduces a precursor to the notion of a chart and of a transition map. Note that it is implicit in Analysis Situs that a manifold obtained as a 'chain' is a subset of Euclidean space.

For example, the unit circle in the plane can be thought of as the graph of the function ${\displaystyle y={\sqrt {1-x^{2}}}}$ or else the function ${\displaystyle y=-{\sqrt {1-x^{2}}}}$ in a neighborhood of every point except the points (1, 0) and (−1, 0); and in a neighborhood of those points, it can be thought of as the graph of, respectively, ${\displaystyle x={\sqrt {1-y^{2}}}}$ and ${\displaystyle x=-{\sqrt {1-y^{2}}}}$. The reason the circle can be represented by a graph in the neighborhood of every point is because the left hand side of its defining equation ${\displaystyle x^{2}+y^{2}-1=0}$ has nonzero gradient at every point of the circle. By the implicit function theorem, every submanifold of Euclidean space is locally the graph of a function.

Hermann Weyl gave an intrinsic definition for differentiable manifolds in his lecture course on Riemann surfaces in 1911–1912, opening the road to the general concept of a topological space that followed shortly. During the 1930s Hassler Whitney and others clarified the foundational aspects of the subject, and thus intuitions dating back to the latter half of the 19th century became precise, and developed through differential geometry and Lie group theory. Notably, the Whitney embedding theorem^[6] showed that the intrinsic definition in terms of charts was equivalent to Poincaré's definition in terms of subsets of Euclidean space.

Topology of manifolds: highlights

Two-dimensional manifolds, also known as a 2D surfaces embedded in our common 3D space, were considered by Riemann under the guise of Riemann surfaces, and rigorously classified in the beginning of the 20th century by Poul Heegaard and Max Dehn. Henri Poincaré pioneered the study of three-dimensional manifolds and raised a fundamental question about them, today known as the Poincaré conjecture. After nearly a century of effort by many mathematicians, starting with Poincaré himself, a consensus among experts (as of 2006) is that Grigori Perelman has proved the Poincaré conjecture (see the Solution of the Poincaré conjecture). William Thurston's geometrization program, formulated in the 1970s, provided a far-reaching extension of the Poincaré conjecture to the general three-dimensional manifolds. Four-dimensional manifolds were brought to the forefront of mathematical research in the 1980s by Michael Freedman and in a different setting, by Simon Donaldson, who was motivated by the then recent progress in theoretical physics (Yang–Mills theory), where they serve as a substitute for ordinary 'flat' spacetime. Andrey Markov Jr. showed in 1960 that no algorithm exists for classifying four-dimensional manifolds. Important work on higher-dimensional manifolds, including analogues of the Poincaré conjecture, had been done earlier by René Thom, John Milnor, Stephen Smale and Sergei Novikov. One of the most pervasive and flexible techniques underlying much work on the topology of manifolds is Morse theory.

Additional structure

Topological manifolds

The simplest kind of manifold to define is the topological manifold, which looks locally like some "ordinary" Euclidean space Rⁿ. Formally, a topological manifold is a topological space locally homeomorphic to a Euclidean space. This means that every point has a neighbourhood for which there exists a homeomorphism (a bijective continuous function whose inverse is also continuous) mapping that neighbourhood to Rⁿ. These homeomorphisms are the charts of the manifold.
It is to be noted that a topological manifold looks locally like a Euclidean space in a rather weak manner: while for each individual chart it is possible to distinguish differentiable functions or measure distances and angles, merely by virtue of being a topological manifold a space does not have any particular and consistent choice of such concepts. In order to discuss such properties for a manifold, one needs to specify further structure and consider differentiable manifolds and Riemannian manifolds discussed below. In particular, the same underlying topological manifold can have several mutually incompatible classes of differentiable functions and an infinite number of ways to specify distances and angles.

Usually additional technical assumptions on the topological space are made to exclude pathological cases. It is customary to require that the space be Hausdorff and second countable.

The dimension of the manifold at a certain point is the dimension of the Euclidean space that the charts at that point map to (number n in the definition). All points in a connected manifold have the same dimension. Some authors require that all charts of a topological manifold map to Euclidean spaces of same dimension. In that case every topological manifold has a topological invariant, its dimension. Other authors allow disjoint unions of topological manifolds with differing dimensions to be called manifolds.

Differentiable manifolds

For most applications a special kind of topological manifold, namely a differentiable manifold, is used. If the local charts on a manifold are compatible in a certain sense, one can define directions, tangent spaces, and differentiable functions on that manifold. In particular it is possible to use calculus on a differentiable manifold. Each point of an n-dimensional differentiable manifold has a tangent space. This is an n-dimensional Euclidean space consisting of the tangent vectors of the curves through the point.

Two important classes of differentiable manifolds are smooth and analytic manifolds. For smooth manifolds the transition maps are smooth, that is infinitely differentiable. Analytic manifolds are smooth manifolds with the additional condition that the transition maps are analytic (they can be expressed as power series). The sphere can be given analytic structure, as can most familiar curves and surfaces.

There are also topological manifolds, i.e., locally Euclidean spaces, which possess no differentiable structures at all.^[7]

A rectifiable set generalizes the idea of a piecewise smooth or rectifiable curve to higher dimensions; however, rectifiable sets are not in general manifolds.

Riemannian manifolds

To measure distances and angles on manifolds, the manifold must be Riemannian. A 'Riemannian manifold' is a differentiable manifold in which each tangent space is equipped with an inner product ⟨⋅,⋅⟩ in a manner which varies smoothly from point to point. Given two tangent vectors u and v, the inner product ⟨u,v⟩ gives a real number. The dot (or scalar) product is a typical example of an inner product. This allows one to define various notions such as length, angles, areas (or volumes), curvature and divergence of vector fields.

All differentiable manifolds (of constant dimension) can be given the structure of a Riemannian manifold. The Euclidean space itself carries a natural structure of Riemannian manifold (the tangent spaces are naturally identified with the Euclidean space itself and carry the standard scalar product of the space). Many familiar curves and surfaces, including for example all n-spheres, are specified as subspaces of a Euclidean space and inherit a metric from their embedding in it.

Finsler manifolds

A Finsler manifold allows the definition of distance but does not require the concept of angle; it is an analytic manifold in which each tangent space is equipped with a norm, ||·||, in a manner which varies smoothly from point to point. This norm can be extended to a metric, defining the length of a curve; but it cannot in general be used to define an inner product.

Any Riemannian manifold is a Finsler manifold.

Lie groups

Lie groups, named after Sophus Lie, are differentiable manifolds that carry also the structure of a group which is such that the group operations are defined by smooth maps.

A Euclidean vector space with the group operation of vector addition is an example of a non-compact Lie group. A simple example of a compact Lie group is the circle: the group operation is simply rotation. This group, known as U(1), can be also characterised as the group of complex numbers of modulus 1 with multiplication as the group operation.

Other examples of Lie groups include special groups of matrices, which are all subgroups of the general linear group, the group of n by n matrices with non-zero determinant. If the matrix entries are real numbers, this will be an n²-dimensional disconnected manifold. The orthogonal groups, the symmetry groups of the sphere and hyperspheres, are n(n−1)/2 dimensional manifolds, where n−1 is the dimension of the sphere. Further examples can be found in the table of Lie groups.

Other types of manifolds

• A complex manifold is a manifold whose charts take values in ${\displaystyle \mathbb {C} ^{n}}$ and whose transition functions are holomorphic on the overlaps. These manifolds are the basic objects of study in complex geometry. A one-complex-dimensional manifold is called a Riemann surface. Note that an n-dimensional complex manifold has dimension 2n as a real differentiable manifold.
• A CR manifold is a manifold modeled on boundaries of domains in ${\displaystyle \mathbb {C} ^{n}}$.
• 'Infinite dimensional manifolds': to allow for infinite dimensions, one may consider Banach manifolds which are locally homeomorphic to Banach spaces. Similarly, Fréchet manifolds are locally homeomorphic to Fréchet spaces.
• A symplectic manifold is a kind of manifold which is used to represent the phase spaces in classical mechanics. They are endowed with a 2-form that defines the Poisson bracket. A closely related type of manifold is a contact manifold.
• A combinatorial manifold is a kind of manifold which is discretization of a manifold. It usually means a piecewise linear manifold made by simplicial complexes.
• A digital manifold is a special kind of combinatorial manifold which is defined in digital space. See digital topology

Classification and invariants

Different notions of manifolds have different notions of classification and invariant; in this section we focus on smooth closed manifolds.

The classification of smooth closed manifolds is well understood in principle, except in dimension 4: in low dimensions (2 and 3) it is geometric, via the uniformization theorem and the solution of the Poincaré conjecture, and in high dimension (5 and above) it is algebraic, via surgery theory. This is a classification in principle: the general question of whether two smooth manifolds are diffeomorphic is not computable in general. Further, specific computations remain difficult, and there are many open questions.

Orientable surfaces can be visualized, and their diffeomorphism classes enumerated, by genus. Given two orientable surfaces, one can determine if they are diffeomorphic by computing their respective genera and comparing: they are diffeomorphic if and only if the genera are equal, so the genus forms a complete set of invariants.

This is much harder in higher dimensions: higher-dimensional manifolds cannot be directly visualized (though visual intuition is useful in understanding them), nor can their diffeomorphism classes be enumerated, nor can one in general determine if two different descriptions of a higher-dimensional manifold refer to the same object.

However, one can determine if two manifolds are different if there is some intrinsic characteristic that differentiates them. Such criteria are commonly referred to as invariants, because, while they may be defined in terms of some presentation (such as the genus in terms of a triangulation), they are the same relative to all possible descriptions of a particular manifold: they are invariant under different descriptions.

Naively, one could hope to develop an arsenal of invariant criteria that would definitively classify all manifolds up to isomorphism. Unfortunately, it is known that for manifolds of dimension 4 and higher, no program exists that can decide whether two manifolds are diffeomorphic.

Smooth manifolds have a rich set of invariants, coming from point-set topology, classic algebraic topology, and geometric topology. The most familiar invariants, which are visible for surfaces, are orientability (a normal invariant, also detected by homology) and genus (a homological invariant).

Smooth closed manifolds have no local invariants (other than dimension), though geometric manifolds have local invariants, notably the curvature of a Riemannian manifold and the torsion of a manifold equipped with an affine connection. This distinction between local invariants and no local invariants is a common way to distinguish between geometry and topology. All invariants of a smooth closed manifold are thus global.

Algebraic topology is a source of a number of important global invariant properties. Some key criteria include the simply connected property and orientability (see below). Indeed, several branches of mathematics, such as homology and homotopy theory, and the theory of characteristic classes were founded in order to study invariant properties of manifolds.

Surfaces

Orientability

In dimensions two and higher, a simple but important invariant criterion is the question of whether a manifold admits a meaningful orientation. Consider a topological manifold with charts mapping to Rⁿ. Given an ordered basis for Rⁿ, a chart causes its piece of the manifold to itself acquire a sense of ordering, which in 3-dimensions can be viewed as either right-handed or left-handed. Overlapping charts are not required to agree in their sense of ordering, which gives manifolds an important freedom. For some manifolds, like the sphere, charts can be chosen so that overlapping regions agree on their "handedness"; these are orientable manifolds. For others, this is impossible. The latter possibility is easy to overlook, because any closed surface embedded (without self-intersection) in three-dimensional space is orientable.

Some illustrative examples of non-orientable manifolds include: (1) the Möbius strip, which is a manifold with boundary, (2) the Klein bottle, which must intersect itself in its 3-space representation, and (3) the real projective plane, which arises naturally in geometry.

Möbius strip

Möbius strip

Begin with an infinite circular cylinder standing vertically, a manifold without boundary. Slice across it high and low to produce two circular boundaries, and the cylindrical strip between them. This is an orientable manifold with boundary, upon which "surgery" will be performed. Slice the strip open, so that it could unroll to become a rectangle, but keep a grasp on the cut ends. Twist one end 180°, making the inner surface face out, and glue the ends back together seamlessly. This results in a strip with a permanent half-twist: the Möbius strip. Its boundary is no longer a pair of circles, but (topologically) a single circle; and what was once its "inside" has merged with its "outside", so that it now has only a single side.

Klein bottle

The Klein bottle immersed in three-dimensional space

Take two Möbius strips; each has a single loop as a boundary. Straighten out those loops into circles, and let the strips distort into cross-caps. Gluing the circles together will produce a new, closed manifold without boundary, the Klein bottle. Closing the surface does nothing to improve the lack of orientability, it merely removes the boundary. Thus, the Klein bottle is a closed surface with no distinction between inside and outside. Note that in three-dimensional space, a Klein bottle's surface must pass through itself. Building a Klein bottle which is not self-intersecting requires four or more dimensions of space.

Real projective plane

Begin with a sphere centered on the origin. Every line through the origin pierces the sphere in two opposite points called antipodes. Although there is no way to do so physically, it is possible (by considering a quotient space) to mathematically merge each antipode pair into a single point. The closed surface so produced is the real projective plane, yet another non-orientable surface. It has a number of equivalent descriptions and constructions, but this route explains its name: all the points on any given line through the origin project to the same "point" on this "plane".

Genus and the Euler characteristic

For two dimensional manifolds a key invariant property is the genus, or the "number of handles" present in a surface. A torus is a sphere with one handle, a double torus is a sphere with two handles, and so on. Indeed, it is possible to fully characterize compact, two-dimensional manifolds on the basis of genus and orientability. In higher-dimensional manifolds genus is replaced by the notion of Euler characteristic, and more generally Betti numbers and homology and cohomology.

Maps of manifolds

A Morin surface, an immersion used in sphere eversion

Just as there are various types of manifolds, there are various types of maps of manifolds. In addition to continuous functions and smooth functions generally, there are maps with special properties. In geometric topology a basic type are embeddings, of which knot theory is a central example, and generalizations such as immersions, submersions, covering spaces, and ramified covering spaces. Basic results include the Whitney embedding theorem and Whitney immersion theorem.

In Riemannian geometry, one may ask for maps to preserve the Riemannian metric, leading to notions of isometric embeddings, isometric immersions, and Riemannian submersions; a basic result is the Nash embedding theorem.

Scalar-valued functions

3D color plot of the spherical harmonics of degree ${\displaystyle n=5}$

A basic example of maps between manifolds are scalar-valued functions on a manifold,

${\displaystyle f\colon M\to \mathbf {R} }$ or ${\displaystyle f\colon M\to \mathbf {C} ,}$

sometimes called regular functions or functionals, by analogy with algebraic geometry or linear algebra. These are of interest both in their own right, and to study the underlying manifold.

In geometric topology, most commonly studied are Morse functions, which yield handlebody decompositions, while in mathematical analysis, one often studies solution to partial differential equations, an important example of which is harmonic analysis, where one studies harmonic functions: the kernel of the Laplace operator. This leads to such functions as the spherical harmonics, and to heat kernel methods of studying manifolds, such as hearing the shape of a drum and some proofs of the Atiyah–Singer index theorem.

Generalizations of manifolds

Infinite dimensional manifolds

The definition of a manifold can be generalized by dropping the requirement of finite dimensionality. Thus an infinite dimensional manifold is a topological space locally homeomorphic to a topological vector space over the reals. This omits the point-set axioms, allowing higher cardinalities and non-Hausdorff manifolds; and it omits finite dimension, allowing structures such as Hilbert manifolds to be modeled on Hilbert spaces, Banach manifolds to be modeled on Banach spaces, and Fréchet manifolds to be modeled on Fréchet spaces. Usually one relaxes one or the other condition: manifolds with the point-set axioms are studied in general topology, while infinite-dimensional manifolds are studied in functional analysis.

Orbifolds

An orbifold is a generalization of manifold allowing for certain kinds of "singularities" in the topology. Roughly speaking, it is a space which locally looks like the quotients of some simple space (e.g. Euclidean space) by the actions of various finite groups. The singularities correspond to fixed points of the group actions, and the actions must be compatible in a certain sense.

Algebraic varieties and schemes

Non-singular algebraic varieties over the real or complex numbers are manifolds. One generalizes this first by allowing singularities, secondly by allowing different fields, and thirdly by emulating the patching construction of manifolds: just as a manifold is glued together from open subsets of Euclidean space, an algebraic variety is glued together from affine algebraic varieties, which are zero sets of polynomials over algebraically closed fields. Schemes are likewise glued together from affine schemes, which are a generalization of algebraic varieties. Both are related to manifolds, but are constructed algebraically using sheaves instead of atlases.

Because of singular points, a variety is in general not a manifold, though linguistically the French variété, German Mannigfaltigkeit and English manifold are largely synonymous. In French an algebraic variety is called une variété algébrique (an algebraic variety), while a smooth manifold is called une variété différentielle (a differential variety).

Stratified space

A "stratified space" is a space that can be divided into pieces ("strata"), with each stratum a manifold, with the strata fitting together in prescribed ways (formally, a filtration by closed subsets). There are various technical definitions, notably a Whitney stratified space (see Whitney conditions) for smooth manifolds and a topologically stratified space for topological manifolds. Basic examples include manifold with boundary (top dimensional manifold and codimension 1 boundary) and manifold with corners (top dimensional manifold, codimension 1 boundary, codimension 2 corners). Whitney stratified spaces are a broad class of spaces, including algebraic varieties, analytic varieties, semialgebraic sets, and subanalytic sets.

CW-complexes

A CW complex is a topological space formed by gluing disks of different dimensionality together. In general the resulting space is singular, and hence not a manifold. However, they are of central interest in algebraic topology, especially in homotopy theory, as they are easy to compute with and singularities are not a concern.

Homology manifolds

A homology manifold is a space that behaves like a manifold from the point of view of homology theory. These are not all manifolds, but (in high dimension) can be analyzed by surgery theory similarly to manifolds, and failure to be a manifold is a local obstruction, as in surgery theory.^[8]

Differential spaces

Let ${\displaystyle M}$ be a nonempty set. Suppose that some family of real functions on ${\displaystyle M}$ was chosen. Denote it by ${\displaystyle C\subseteq \mathbb {R} ^{M}}$. It is an algebra with respect to the pointwise addition and multiplication. Let ${\displaystyle M}$ be equipped with the topology induced by ${\displaystyle C}$. Suppose also that the following conditions hold. First: for every ${\displaystyle H\in C^{\infty }\left(\mathbb {R} ^{i}\right)}$, where ${\displaystyle i\in \mathbb {N} }$, and arbitrary ${\displaystyle f_{1},\dots ,f_{n}\in C}$, the composition ${\displaystyle H\circ \left(f_{1},\dots ,f_{n}\right)\in C}$. Second: every function, which in every point of ${\displaystyle M}$ locally coincides with some function from ${\displaystyle C}$, also belongs to ${\displaystyle C}$. A pair ${\displaystyle (M,C)}$ for which the above conditions hold, is called a Sikorski differential space.^[9][10]

Bernhard Riemann

From Wikipedia, the free encyclopedia


Bernhard Riemann
Bernhard Riemann in 1863.
Born	Georg Friedrich Bernhard Riemann 17 September 1826 Breselenz, Kingdom of Hanover (modern-day Germany)
Died	20 July 1866 (aged 39) Selasca, Kingdom of Italy
Residence	Kingdom of Hanover
Nationality	German
Alma mater	University of Göttingen University of Berlin
Known for	See list
Scientific career
Fields	Mathematics Physics
Institutions	University of Göttingen
Thesis	Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen complexen Größe (1851)
Doctoral advisor	Carl Friedrich Gauss
Other academic advisors	Gotthold Eisenstein Moritz A. Stern Carl W. B. Goldschmidt
Notable students	Gustav Roch Eduard Selling
Influences	J. P. G. L. Dirichlet
Signature

Georg Friedrich Bernhard Riemann (German: [ˈʀiːman] ( listen); 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His famous 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as one of the most influential papers in analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity.

Biography

Early years

Riemann was born on September 17, 1826 in Breselenz, a village near Dannenberg in the Kingdom of Hanover. His father, Friedrich Bernhard Riemann, was a poor Lutheran pastor in Breselenz who fought in the Napoleonic Wars. His mother, Charlotte Ebell, died before her children had reached adulthood. Riemann was the second of six children, shy and suffering from numerous nervous breakdowns. Riemann exhibited exceptional mathematical skills, such as calculation abilities, from an early age but suffered from timidity and a fear of speaking in public.


Education

During 1840, Riemann went to Hanover to live with his grandmother and attend lyceum (middle school). After the death of his grandmother in 1842, he attended high school at the Johanneum Lüneburg. In high school, Riemann studied the Bible intensively, but he was often distracted by mathematics. His teachers were amazed by his adept ability to perform complicated mathematical operations, in which he often outstripped his instructor's knowledge. In 1846, at the age of 19, he started studying philology and Christian theology in order to become a pastor and help with his family's finances.

During the spring of 1846, his father, after gathering enough money, sent Riemann to the University of Göttingen, where he planned to study towards a degree in Theology. However, once there, he began studying mathematics under Carl Friedrich Gauss (specifically his lectures on the method of least squares). Gauss recommended that Riemann give up his theological work and enter the mathematical field; after getting his father's approval, Riemann transferred to the University of Berlin in 1847.^[1] During his time of study, Carl Gustav Jacob Jacobi, Peter Gustav Lejeune Dirichlet, Jakob Steiner, and Gotthold Eisenstein were teaching. He stayed in Berlin for two years and returned to Göttingen in 1849.


Academia

Riemann held his first lectures in 1854, which founded the field of Riemannian geometry and thereby set the stage for Albert Einstein's general theory of relativity. In 1857, there was an attempt to promote Riemann to extraordinary professor status at the University of Göttingen. Although this attempt failed, it did result in Riemann finally being granted a regular salary. In 1859, following Dirichlet's death, he was promoted to head the mathematics department at the University of Göttingen. He was also the first to suggest using dimensions higher than merely three or four in order to describe physical reality.^[2] In 1862 he married Elise Koch and had a daughter.


Austro-Prussian War and death in Italy


Riemann's tombstone in Biganzolo in Piedmont, Italy.

Riemann fled Göttingen when the armies of Hanover and Prussia clashed there in 1866.^[3] He died of tuberculosis during his third journey to Italy in Selasca (now a hamlet of Verbania on Lake Maggiore) where he was buried in the cemetery in Biganzolo (Verbania). Riemann was a dedicated Christian, the son of a Protestant minister, and saw his life as a mathematician as another way to serve God. During his life, he held closely to his Christian faith and considered it to be the most important aspect of his life. At the time of his death, he was reciting the Lord’s Prayer with his wife and died before they finished saying the prayer.^[4] Meanwhile, in Göttingen his housekeeper discarded some of the papers in his office, including much unpublished work. Riemann refused to publish incomplete work, and some deep insights may have been lost forever.^[3]

Riemann's tombstone in Biganzolo (Italy) refers to Romans 8:28 ("And we know that all things work together for good to them that love God, to them who are called according to his purpose"):

Here rests in God Georg Friedrich Bernhard Riemann
Professor in Göttingen
born in Breselenz, Germany 17 September 1826
died in Selasca, Italy 20 July 1866
For those who love God, all things must work together for the best.^[5]


Riemannian geometry

Riemann's published works opened up research areas combining analysis with geometry. These would subsequently become major parts of the theories of Riemannian geometry, algebraic geometry, and complex manifold theory. The theory of Riemann surfaces was elaborated by Felix Klein and particularly Adolf Hurwitz. This area of mathematics is part of the foundation of topology and is still being applied in novel ways to mathematical physics.

In 1853, Gauss asked his student Riemann to prepare a Habilitationsschrift on the foundations of geometry. Over many months, Riemann developed his theory of higher dimensions and delivered his lecture at Göttingen in 1854 entitled "Ueber die Hypothesen welche der Geometrie zu Grunde liegen" ("On the hypotheses which underlie geometry"). It was only published twelve years later in 1868 by Dedekind, two years after his death. Its early reception appears to have been slow but it is now recognized as one of the most important works in geometry.

The subject founded by this work is Riemannian geometry. Riemann found the correct way to extend into n dimensions the differential geometry of surfaces, which Gauss himself proved in his theorema egregium. The fundamental object is called the Riemann curvature tensor. For the surface case, this can be reduced to a number (scalar), positive, negative, or zero; the non-zero and constant cases being models of the known non-Euclidean geometries.

Riemann's idea was to introduce a collection of numbers at every point in space (i.e., a tensor) which would describe how much it was bent or curved. Riemann found that in four spatial dimensions, one needs a collection of ten numbers at each point to describe the properties of a manifold, no matter how distorted it is. This is the famous construction central to his geometry, known now as a Riemannian metric.


Complex analysis

In his dissertation, he established a geometric foundation for complex analysis through Riemann surfaces, through which multi-valued functions like the logarithm (with infinitely many sheets) or the square root (with two sheets) could become one-to-one functions. Complex functions are harmonic functions (that is, they satisfy Laplace's equation and thus the Cauchy–Riemann equations) on these surfaces and are described by the location of their singularities and the topology of the surfaces. The topological "genus" of the Riemann surfaces is given by ${\displaystyle g=w/2-n+1}$, where the surface has ${\displaystyle n}$ leaves coming together at ${\displaystyle w}$ branch points. For ${\displaystyle g>1}$ the Riemann surface has ${\displaystyle (3g-3)}$ parameters (the "moduli").

His contributions to this area are numerous. The famous Riemann mapping theorem says that a simply connected domain in the complex plane is "biholomorphically equivalent" (i.e. there is a bijection between them that is holomorphic with a holomorphic inverse) to either ${\displaystyle \mathbb {C} }$ or to the interior of the unit circle. The generalization of the theorem to Riemann surfaces is the famous uniformization theorem, which was proved in the 19th century by Henri Poincaré and Felix Klein. Here, too, rigorous proofs were first given after the development of richer mathematical tools (in this case, topology). For the proof of the existence of functions on Riemann surfaces he used a minimality condition, which he called the Dirichlet principle. Karl Weierstrass found a gap in the proof: Riemann had not noticed that his working assumption (that the minimum existed) might not work; the function space might not be complete, and therefore the existence of a minimum was not guaranteed. Through the work of David Hilbert in the Calculus of Variations, the Dirichlet principle was finally established. Otherwise, Weierstrass was very impressed with Riemann, especially with his theory of abelian functions. When Riemann's work appeared, Weierstrass withdrew his paper from Crelle's Journal and did not publish it. They had a good understanding when Riemann visited him in Berlin in 1859. Weierstrass encouraged his student Hermann Amandus Schwarz to find alternatives to the Dirichlet principle in complex analysis, in which he was successful. An anecdote from Arnold Sommerfeld^[6] shows the difficulties which contemporary mathematicians had with Riemann's new ideas. In 1870, Weierstrass had taken Riemann's dissertation with him on a holiday to Rigi and complained that it was hard to understand. The physicist Hermann von Helmholtz assisted him in the work over night and returned with the comment that it was "natural" and "very understandable".

Other highlights include his work on abelian functions and theta functions on Riemann surfaces. Riemann had been in a competition with Weierstrass since 1857 to solve the Jacobian inverse problems for abelian integrals, a generalization of elliptic integrals. Riemann used theta functions in several variables and reduced the problem to the determination of the zeros of these theta functions. Riemann also investigated period matrices and characterized them through the "Riemannian period relations" (symmetric, real part negative). By Ferdinand Georg Frobenius and Solomon Lefschetz the validity of this relation is equivalent with the embedding of ${\displaystyle \mathbb {C} ^{n}/\Omega }$ (where ${\displaystyle \Omega }$ is the lattice of the period matrix) in a projective space by means of theta functions. For certain values of ${\displaystyle n}$, this is the Jacobian variety of the Riemann surface, an example of an abelian manifold.

Many mathematicians such as Alfred Clebsch furthered Riemann's work on algebraic curves. These theories depended on the properties of a function defined on Riemann surfaces. For example, the Riemann–Roch theorem (Roch was a student of Riemann) says something about the number of linearly independent differentials (with known conditions on the zeros and poles) of a Riemann surface.

According to Detlef Laugwitz,^[7] automorphic functions appeared for the first time in an essay about the Laplace equation on electrically charged cylinders. Riemann however used such functions for conformal maps (such as mapping topological triangles to the circle) in his 1859 lecture on hypergeometric functions or in his treatise on minimal surfaces.


Real analysis

In the field of real analysis, he discovered the Riemann integral in his habilitation. Among other things, he showed that every piecewise continuous function is integrable. Similarly, the Stieltjes integral goes back to the Göttinger mathematician, and so they are named together the Riemann–Stieltjes integral.

In his habilitation work on Fourier series, where he followed the work of his teacher Dirichlet, he showed that Riemann-integrable functions are "representable" by Fourier series. Dirichlet has shown this for continuous, piecewise-differentiable functions (thus with countably many non-differentiable points). Riemann gave an example of a Fourier series representing a continuous, almost nowhere-differentiable function, a case not covered by Dirichlet. He also proved the Riemann–Lebesgue lemma: if a function is representable by a Fourier series, then the Fourier coefficients go to zero for large n.

Riemann's essay was also the starting point for Georg Cantor's work with Fourier series, which was the impetus for set theory.

He also worked with hypergeometric differential equations in 1857 using complex analytical methods and presented the solutions through the behavior of closed paths about singularities (described by the monodromy matrix). The proof of the existence of such differential equations by previously known monodromy matrices is one of the Hilbert problems.


Number theory

He made some famous contributions to modern analytic number theory. In a single short paper, the only one he published on the subject of number theory, he investigated the zeta function that now bears his name, establishing its importance for understanding the distribution of prime numbers. The Riemann hypothesis was one of a series of conjectures he made about the function's properties.

In Riemann's work, there are many more interesting developments. He proved the functional equation for the zeta function (already known to Leonhard Euler), behind which a theta function lies. Through the summation of this approximation function over the non-trivial zeros on the line with real portion 1/2, he gave an exact, "explicit formula" for ${\displaystyle \pi (x)}$.

Riemann knew of Pafnuty Chebyshev's work on the Prime Number Theorem. He had visited Dirichlet in 1852.


Writings

• 1868 On the hypotheses which lie at the foundation of geometry, translated by W.K.Clifford, Nature 8 1873 183 – reprinted in Clifford's Collected Mathematical Papers, London 1882 (MacMillan); New York 1968 (Chelsea) http://www.emis.de/classics/Riemann/. Also in Ewald, William B., ed., 1996 “From Kant to Hilbert: A Source Book in the Foundations of Mathematics”, 2 vols. Oxford Uni. Press: 652–61.
• 1892 Collected Works of Bernhardt Riemann (H. Weber ed). In German. Reprinted New York 1953 (Dover)
• Riemann, Bernhard (2004), Collected papers, Kendrick Press, Heber City, UT, ISBN 978-0-9740427-2-5, MR 2121437