A total solar eclipse occurs when the Moon completely covers the Sun's disk, as seen in this 1999 solar eclipse. Solar prominences can be seen along the limb (in red) as well as extensive coronal filaments. | |
  An annular solar eclipse (left) occurs when the Moon is too far away to completely cover the Sun's disk (May 20, 2012). During a partial solar eclipse (right), the Moon blocks only part of the Sun's disk (October 23, 2014). |
A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby obscuring Earth's view of the Sun, totally or partially. Such an alignment coincides with a new moon, indicating the Moon is closest to the plane of the Earth's orbit. In a total eclipse, the disk of the Sun is fully obscured by the Moon. In partial and annular eclipses, only part of the Sun is obscured.
If the Moon were in a perfectly circular orbit and in the same orbital plane as Earth, there would be total solar eclipses every new moon. Instead, because the Moon's orbit is tilted at about 5 degrees to Earth's orbit, its shadow usually misses Earth. Solar (and lunar) eclipses therefore happen only during eclipse seasons, resulting in at least two, and up to five, solar eclipses each year, no more than two of which can be total. Total eclipses are more rare because they require a more precise alignment between the centers of the Sun and Moon, and because the Moon's apparent size in the sky is sometimes too small to fully cover the Sun. Total solar eclipses occur rarely at a given place on Earth, on average about every 360 to 410 years.
An eclipse is a natural phenomenon. In some ancient and modern cultures, solar eclipses were attributed to supernatural causes or regarded as bad omens. Astronomers' predictions of eclipses began in China as early as the 4th century BC; eclipses hundreds of years into the future may now be predicted with high accuracy.
Looking directly at the Sun can lead to permanent eye damage, so special eye protection or indirect viewing techniques are used when viewing a solar eclipse. Only the total phase of a total solar eclipse is safe to view without protection. Enthusiasts known as eclipse chasers or umbraphiles travel to remote locations to see solar eclipses.
Types
There are four types of solar eclipses:
- A total eclipse occurs when the dark silhouette of the Moon completely obscures the intensely bright light of the Sun, allowing the much fainter solar corona to be visible. During any one eclipse, totality occurs at best only in a narrow track on the surface of Earth. This narrow track is called the path of totality.
- An annular eclipse occurs when the Sun and Moon are exactly in line with the Earth, but the apparent size of the Moon is smaller than that of the Sun. Hence the Sun appears as a very bright ring, or annulus, surrounding the dark disk of the Moon.
- A hybrid eclipse (also called annular/total eclipse) shifts between a total and annular eclipse. At certain points on the surface of Earth, it appears as a total eclipse, whereas at other points it appears as annular. Hybrid eclipses are comparatively rare.
- A partial eclipse occurs when the Sun and Moon are not exactly in line with the Earth and the Moon only partially obscures the Sun. This phenomenon can usually be seen from a large part of the Earth outside of the track of an annular or total eclipse. However, some eclipses can be seen only as a partial eclipse, because the umbra passes above the Earth's polar regions and never intersects the Earth's surface. Partial eclipses are virtually unnoticeable in terms of the Sun's brightness, as it takes well over 90% coverage to notice any darkening at all. Even at 99%, it would be no darker than civil twilight. Of course, partial eclipses (and partial stages of other eclipses) can be observed if one is viewing the Sun through a darkening filter (which should always be used for safety).
The Sun's distance from Earth is about 400 times the Moon's distance, and the Sun's diameter is about 400 times the Moon's diameter. Because these ratios are approximately the same, the Sun and the Moon as seen from Earth appear to be approximately the same size: about 0.5 degree of arc in angular measure.
A separate category of solar eclipses is that of the Sun being occluded by a body other than the Earth's Moon, as can be observed at points in space away from the Earth's surface. Two examples are when the crew of Apollo 12 observed the Earth eclipse the Sun in 1969 and when the Cassini probe observed Saturn eclipsing the Sun in 2006.
The Moon's orbit around the Earth is slightly elliptical, as is the Earth's orbit around the Sun. The apparent sizes of the Sun and Moon therefore vary. The magnitude of an eclipse is the ratio of the apparent size of the Moon to the apparent size of the Sun during an eclipse. An eclipse that occurs when the Moon is near its closest distance to Earth (i.e., near its perigee) can be a total eclipse because the Moon will appear to be large enough to completely cover the Sun's bright disk or photosphere; a total eclipse has a magnitude greater than or equal to 1.000. Conversely, an eclipse that occurs when the Moon is near its farthest distance from Earth (i.e., near its apogee) can be only an annular eclipse because the Moon will appear to be slightly smaller than the Sun; the magnitude of an annular eclipse is less than 1.
A hybrid eclipse occurs when the magnitude of an eclipse changes during the event from less to greater than one, so the eclipse appears to be total at locations nearer the midpoint, and annular at other locations nearer the beginning and end, since the sides of the Earth are slightly further away from the Moon. These eclipses are extremely narrow in their path width and relatively short in their duration at any point compared with fully total eclipses; the 2023 April 20 hybrid eclipse's totality is over a minute in duration at various points along the path of totality. Like a focal point, the width and duration of totality and annularity are near zero at the points where the changes between the two occur.
Because the Earth's orbit around the Sun is also elliptical, the Earth's distance from the Sun similarly varies throughout the year. This affects the apparent size of the Sun in the same way, but not as much as does the Moon's varying distance from Earth. When Earth approaches its farthest distance from the Sun in early July, a total eclipse is somewhat more likely, whereas conditions favour an annular eclipse when Earth approaches its closest distance to the Sun in early January.
Terminology for central eclipse
Central eclipse is often used as a generic term for a total, annular, or hybrid eclipse. This is, however, not completely correct: the definition of a central eclipse is an eclipse during which the central line of the umbra touches the Earth's surface. It is possible, though extremely rare, that part of the umbra intersects with the Earth (thus creating an annular or total eclipse), but not its central line. This is then called a non-central total or annular eclipse. Gamma is a measure of how centrally the shadow strikes. The last (umbral yet) non-central solar eclipse was on April 29, 2014. This was an annular eclipse. The next non-central total solar eclipse will be on April 9, 2043.
The visual phases observed during a total eclipse are called:
- First contact—when the Moon's limb (edge) is exactly tangential to the Sun's limb.
- Second contact—starting with Baily's Beads (caused by light shining through valleys on the Moon's surface) and the diamond ring effect. Almost the entire disk is covered.
- Totality—the Moon obscures the entire disk of the Sun and only the solar corona is visible.
- Third contact—when the first bright light becomes visible and the Moon's shadow is moving away from the observer. Again a diamond ring may be observed.
- Fourth contact—when the trailing edge of the Moon ceases to overlap with the solar disk and the eclipse ends.
Predictions
Geometry
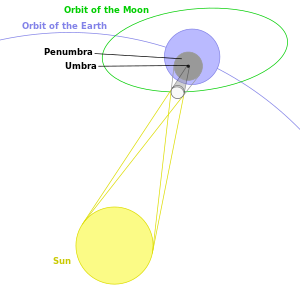
The diagrams to the right show the alignment of the Sun, Moon, and Earth during a solar eclipse. The dark gray region between the Moon and Earth is the umbra, where the Sun is completely obscured by the Moon. The small area where the umbra touches Earth's surface is where a total eclipse can be seen. The larger light gray area is the penumbra, in which a partial eclipse can be seen. An observer in the antumbra, the area of shadow beyond the umbra, will see an annular eclipse.
The Moon's orbit around the Earth is inclined at an angle of just over 5 degrees to the plane of the Earth's orbit around the Sun (the ecliptic). Because of this, at the time of a new moon, the Moon will usually pass to the north or south of the Sun. A solar eclipse can occur only when a new moon occurs close to one of the points (known as nodes) where the Moon's orbit crosses the ecliptic.
As noted above, the Moon's orbit is also elliptical. The Moon's distance from the Earth can vary by about 6% from its average value. Therefore, the Moon's apparent size varies with its distance from the Earth, and it is this effect that leads to the difference between total and annular eclipses. The distance of the Earth from the Sun also varies during the year, but this is a smaller effect. On average, the Moon appears to be slightly smaller than the Sun as seen from the Earth, so the majority (about 60%) of central eclipses are annular. It is only when the Moon is closer to the Earth than average (near its perigee) that a total eclipse occurs.
The Moon orbits the Earth in approximately 27.3 days, relative to a fixed frame of reference. This is known as the sidereal month. However, during one sidereal month, Earth has revolved part way around the Sun, making the average time between one new moon and the next longer than the sidereal month: it is approximately 29.5 days. This is known as the synodic month and corresponds to what is commonly called the lunar month.
The Moon crosses from south to north of the ecliptic at its ascending node, and vice versa at its descending node. However, the nodes of the Moon's orbit are gradually moving in a retrograde motion, due to the action of the Sun's gravity on the Moon's motion, and they make a complete circuit every 18.6 years. This regression means that the time between each passage of the Moon through the ascending node is slightly shorter than the sidereal month. This period is called the nodical or draconic month.
Finally, the Moon's perigee is moving forwards or precessing in its orbit and makes a complete circuit in 8.85 years. The time between one perigee and the next is slightly longer than the sidereal month and known as the anomalistic month.
The Moon's orbit intersects with the ecliptic at the two nodes that are 180 degrees apart. Therefore, the new moon occurs close to the nodes at two periods of the year approximately six months (173.3 days) apart, known as eclipse seasons, and there will always be at least one solar eclipse during these periods. Sometimes the new moon occurs close enough to a node during two consecutive months to eclipse the Sun on both occasions in two partial eclipses. This means that, in any given year, there will always be at least two solar eclipses, and there can be as many as five.
Eclipses can occur only when the Sun is within about 15 to 18 degrees of a node, (10 to 12 degrees for central eclipses). This is referred to as an eclipse limit, and is given in ranges because the apparent sizes and speeds of the Sun and Moon vary throughout the year. In the time it takes for the Moon to return to a node (draconic month), the apparent position of the Sun has moved about 29 degrees, relative to the nodes. Since the eclipse limit creates a window of opportunity of up to 36 degrees (24 degrees for central eclipses), it is possible for partial eclipses (or rarely a partial and a central eclipse) to occur in consecutive months.
Path
During a central eclipse, the Moon's umbra (or antumbra, in the case of an annular eclipse) moves rapidly from west to east across the Earth. The Earth is also rotating from west to east, at about 28 km/min at the Equator, but as the Moon is moving in the same direction as the Earth's rotation at about 61 km/min, the umbra almost always appears to move in a roughly west–east direction across a map of the Earth at the speed of the Moon's orbital velocity minus the Earth's rotational velocity. Rare exceptions can occur in polar regions where the path may go over or near the pole, as in 2021 on June 10 and December 4.
The width of the track of a central eclipse varies according to the relative apparent diameters of the Sun and Moon. In the most favourable circumstances, when a total eclipse occurs very close to perigee, the track can be up to 267 km (166 mi) wide and the duration of totality may be over 7 minutes. Outside of the central track, a partial eclipse is seen over a much larger area of the Earth. Typically, the umbra is 100–160 km wide, while the penumbral diameter is in excess of 6400 km.
Besselian elements are used to predict whether an eclipse will be partial, annular, or total (or annular/total), and what the eclipse circumstances will be at any given location. Calculations with Besselian elements can determine the exact shape of the umbra's shadow on the Earth's surface. But at what longitudes on the Earth's surface the shadow will fall, is a function of the Earth's rotation, and on how much that rotation has slowed down over time. A number called ΔT is used in eclipse prediction to take this slowing into account. As the Earth slows, ΔT increases. ΔT for dates in the future can only be roughly estimated because the Earth's rotation is slowing irregularly. This means that, although it is possible to predict that there will be a total eclipse on a certain date in the far future, it is not possible to predict in the far future exactly at what longitudes that eclipse will be total. Historical records of eclipses allow estimates of past values of ΔT and so of the Earth's rotation.
Duration
The following factors determine the duration of a total solar eclipse (in order of decreasing importance):
- The Moon being almost exactly at perigee (making its angular diameter as large as possible).
- The Earth being very near aphelion (furthest away from the Sun in its elliptical orbit, making its angular diameter nearly as small as possible).
- The midpoint of the eclipse being very close to the Earth's equator, where the rotational velocity is greatest.
- The vector of the eclipse path at the midpoint of the eclipse aligning with the vector of the Earth's rotation (i.e. not diagonal but due east).
- The midpoint of the eclipse being near the subsolar point (the part of the Earth closest to the Sun).
The longest eclipse that has been calculated thus far is the eclipse of July 16, 2186 (with a maximum duration of 7 minutes 29 seconds over northern Guyana).
Occurrence and cycles
Total solar eclipses are rare events. Although they occur somewhere on Earth every 18 months on average, it is estimated that they recur at any given place only once every 360 to 410 years, on average. The total eclipse lasts for only a maximum of a few minutes at any location, because the Moon's umbra moves eastward at over 1700 km/h. Totality currently can never last more than 7 min 32 s. This value changes over the millennia and is currently decreasing. By the 8th millennium, the longest theoretically possible total eclipse will be less than 7 min 2 s. The last time an eclipse longer than 7 minutes occurred was June 30, 1973 (7 min 3 sec). Observers aboard a Concorde supersonic aircraft were able to stretch totality for this eclipse to about 74 minutes by flying along the path of the Moon's umbra. The next total eclipse exceeding seven minutes in duration will not occur until June 25, 2150. The longest total solar eclipse during the 11,000 year period from 3000 BC to at least 8000 AD will occur on July 16, 2186, when totality will last 7 min 29 s. For comparison, the longest total eclipse of the 20th century at 7 min 8 s occurred on June 20, 1955, and there are no total solar eclipses over 7 min in duration in the 21st century.
It is possible to predict other eclipses using eclipse cycles. The saros is probably the best known and one of the most accurate. A saros lasts 6,585.3 days (a little over 18 years), which means that, after this period, a practically identical eclipse will occur. The most notable difference will be a westward shift of about 120° in longitude (due to the 0.3 days) and a little in latitude (north-south for odd-numbered cycles, the reverse for even-numbered ones). A saros series always starts with a partial eclipse near one of Earth's polar regions, then shifts over the globe through a series of annular or total eclipses, and ends with a partial eclipse at the opposite polar region. A saros series lasts 1226 to 1550 years and 69 to 87 eclipses, with about 40 to 60 of them being central.
Frequency per year
Between two and five solar eclipses occur every year, with at least one per eclipse season. Since the Gregorian calendar was instituted in 1582, years that have had five solar eclipses were 1693, 1758, 1805, 1823, 1870, and 1935. The next occurrence will be 2206. On average, there are about 240 solar eclipses each century.
| January 5 | February 3 | June 30 | July 30 | December 25 |
|---|---|---|---|---|
| Partial (south) |
Partial (north) |
Partial (north) |
Partial (south) |
Annular (south) |
 Saros 111 |
 Saros 149 |
 Saros 116 |
 Saros 154 |
 Saros 121 |
Final totality
Total solar eclipses are seen on Earth because of a fortuitous combination of circumstances. Even on Earth, the diversity of eclipses familiar to people today is a temporary (on a geological time scale) phenomenon. Hundreds of millions of years in the past, the Moon was closer to the Earth and therefore apparently larger, so every solar eclipse was total or partial, and there were no annular eclipses. Due to tidal acceleration, the orbit of the Moon around the Earth becomes approximately 3.8 cm more distant each year. Millions of years in the future, the Moon will be too far away to fully occlude the Sun, and no total eclipses will occur. In the same timeframe, the Sun may become brighter, making it appear larger in size. Estimates of the time when the Moon will be unable to occlude the entire Sun when viewed from the Earth range between 650 million and 1.4 billion years in the future.
Historical eclipses
Historical eclipses are a very valuable resource for historians, in that they allow a few historical events to be dated precisely, from which other dates and ancient calendars may be deduced.[46] A solar eclipse of June 15, 763 BC mentioned in an Assyrian text is important for the chronology of the ancient Near East. There have been other claims to date earlier eclipses. The Book of Joshua 10:13 describes the sun staying still for an entire day in the sky; a group of University of Cambridge scholars concluded this to be the annular solar eclipse that occurred on 30 October 1207 BC. The Chinese king Zhong Kang supposedly beheaded two astronomers, Hsi and Ho, who failed to predict an eclipse 4,000 years ago. Perhaps the earliest still-unproven claim is that of archaeologist Bruce Masse, who putatively links an eclipse that occurred on May 10, 2807, BC with a possible meteor impact in the Indian Ocean on the basis of several ancient flood myths that mention a total solar eclipse.
Eclipses have been interpreted as omens, or portents. The ancient Greek historian Herodotus wrote that Thales of Miletus predicted an eclipse that occurred during a battle between the Medes and the Lydians. Both sides put down their weapons and declared peace as a result of the eclipse. The exact eclipse involved remains uncertain, although the issue has been studied by hundreds of ancient and modern authorities. One likely candidate took place on May 28, 585 BC, probably near the Halys river in Asia Minor. An eclipse recorded by Herodotus before Xerxes departed for his expedition against Greece,[54] which is traditionally dated to 480 BC, was matched by John Russell Hind to an annular eclipse of the Sun at Sardis on February 17, 478 BC. Alternatively, a partial eclipse was visible from Persia on October 2, 480 BC. Herodotus also reports a solar eclipse at Sparta during the Second Persian invasion of Greece. The date of the eclipse (August 1, 477 BC) does not match exactly the conventional dates for the invasion accepted by historians.
Chinese records of eclipses begin at around 720 BC.[59] The 4th century BC astronomer Shi Shen described the prediction of eclipses by using the relative positions of the Moon and Sun.
Attempts have been made to establish the exact date of Good Friday by assuming that the darkness described at Jesus's crucifixion was a solar eclipse. This research has not yielded conclusive results, and Good Friday is recorded as being at Passover, which is held at the time of a full moon. Further, the darkness lasted from the sixth hour to the ninth, or three hours, which is much, much longer than the eight-minute upper limit for any solar eclipse's totality. Contemporary chronicles wrote about an eclipse at the beginning of May 664 that coincided with the beginning of the plague of 664 in the British isles. In the Western hemisphere, there are few reliable records of eclipses before AD 800, until the advent of Arab and monastic observations in the early medieval period. The Cairo astronomer Ibn Yunus wrote that the calculation of eclipses was one of the many things that connect astronomy with the Islamic law, because it allowed knowing when a special prayer can be made. The first recorded observation of the corona was made in Constantinople in AD 968.
The first known telescopic observation of a total solar eclipse was made in France in 1706. Nine years later, English astronomer Edmund Halley accurately predicted and observed the solar eclipse of May 3, 1715. By the mid-19th century, scientific understanding of the Sun was improving through observations of the Sun's corona during solar eclipses. The corona was identified as part of the Sun's atmosphere in 1842, and the first photograph (or daguerreotype) of a total eclipse was taken of the solar eclipse of July 28, 1851. Spectroscope observations were made of the solar eclipse of August 18, 1868, which helped to determine the chemical composition of the Sun.
John Fiske summed up myths about the solar eclipse like this in his 1872 book Myth and Myth-Makers,
the myth of Hercules and Cacus, the fundamental idea is the victory of the solar god over the robber who steals the light. Now whether the robber carries off the light in the evening when Indra has gone to sleep, or boldly rears his black form against the sky during the daytime, causing darkness to spread over the earth, would make little difference to the framers of the myth. To a chicken a solar eclipse is the same thing as nightfall, and he goes to roost accordingly. Why, then, should the primitive thinker have made a distinction between the darkening of the sky caused by black clouds and that caused by the rotation of the earth? He had no more conception of the scientific explanation of these phenomena than the chicken has of the scientific explanation of an eclipse. For him it was enough to know that the solar radiance was stolen, in the one case as in the other, and to suspect that the same demon was to blame for both robberies.
Viewing
Looking directly at the photosphere of the Sun (the bright disk of the Sun itself), even for just a few seconds, can cause permanent damage to the retina of the eye, because of the intense visible and invisible radiation that the photosphere emits. This damage can result in impairment of vision, up to and including blindness. The retina has no sensitivity to pain, and the effects of retinal damage may not appear for hours, so there is no warning that injury is occurring.
Under normal conditions, the Sun is so bright that it is difficult to stare at it directly. However, during an eclipse, with so much of the Sun covered, it is easier and more tempting to stare at it. Looking at the Sun during an eclipse is as dangerous as looking at it outside an eclipse, except during the brief period of totality, when the Sun's disk is completely covered (totality occurs only during a total eclipse and only very briefly; it does not occur during a partial or annular eclipse). Viewing the Sun's disk through any kind of optical aid (binoculars, a telescope, or even an optical camera viewfinder) is extremely hazardous and can cause irreversible eye damage within a fraction of a second.
Partial and annular eclipses
Viewing the Sun during partial and annular eclipses (and during total eclipses outside the brief period of totality) requires special eye protection, or indirect viewing methods if eye damage is to be avoided. The Sun's disk can be viewed using appropriate filtration to block the harmful part of the Sun's radiation. Sunglasses do not make viewing the Sun safe. Only properly designed and certified solar filters should be used for direct viewing of the Sun's disk. Especially, self-made filters using common objects such as a floppy disk removed from its case, a Compact Disc, a black colour slide film, smoked glass, etc. must be avoided.
The safest way to view the Sun's disk is by indirect projection. This can be done by projecting an image of the disk onto a white piece of paper or card using a pair of binoculars (with one of the lenses covered), a telescope, or another piece of cardboard with a small hole in it (about 1 mm diameter), often called a pinhole camera. The projected image of the Sun can then be safely viewed; this technique can be used to observe sunspots, as well as eclipses. Care must be taken, however, to ensure that no one looks through the projector (telescope, pinhole, etc.) directly. Viewing the Sun's disk on a video display screen (provided by a video camera or digital camera) is safe, although the camera itself may be damaged by direct exposure to the Sun. The optical viewfinders provided with some video and digital cameras are not safe. Securely mounting #14 welder's glass in front of the lens and viewfinder protects the equipment and makes viewing possible. Professional workmanship is essential because of the dire consequences any gaps or detaching mountings will have. In the partial eclipse path, one will not be able to see the corona or nearly complete darkening of the sky. However, depending on how much of the Sun's disk is obscured, some darkening may be noticeable. If three-quarters or more of the Sun is obscured, then an effect can be observed by which the daylight appears to be dim, as if the sky were overcast, yet objects still cast sharp shadows.
Totality
When the shrinking visible part of the photosphere becomes very small, Baily's beads will occur. These are caused by the sunlight still being able to reach the Earth through lunar valleys. Totality then begins with the diamond ring effect, the last bright flash of sunlight.
It is safe to observe the total phase of a solar eclipse directly only when the Sun's photosphere is completely covered by the Moon, and not before or after totality. During this period, the Sun is too dim to be seen through filters. The Sun's faint corona will be visible, and the chromosphere, solar prominences, and possibly even a solar flare may be seen. At the end of totality, the same effects will occur in reverse order, and on the opposite side of the Moon.
Eclipse chasing
A dedicated group of eclipse chasers have pursued the observation of solar eclipses when they occur around the Earth. A person who chases eclipses is known as an umbraphile, meaning shadow lover. Umbraphiles travel for eclipses and use various tools to help view the sun including solar viewing glasses, also known as eclipse glasses, as well as telescopes.
Photography
Photographing an eclipse is possible with fairly common camera equipment. In order for the disk of the Sun/Moon to be easily visible, a fairly high magnification long focus lens is needed (at least 200 mm for a 35 mm camera), and for the disk to fill most of the frame, a longer lens is needed (over 500 mm). As with viewing the Sun directly, looking at it through the optical viewfinder of a camera can produce damage to the retina, so care is recommended. Solar filters are required for digital photography even if an optical viewfinder is not used. Using a camera's live view feature or an electronic viewfinder is safe for the human eye, but the Sun's rays could potentially irreparably damage digital image sensors unless the lens is covered by a properly designed solar filter.
Other observations
A total solar eclipse provides a rare opportunity to observe the corona (the outer layer of the Sun's atmosphere). Normally this is not visible because the photosphere is much brighter than the corona. According to the point reached in the solar cycle, the corona may appear small and symmetric, or large and fuzzy. It is very hard to predict this in advance.
As the light filters through leaves of trees during a partial eclipse, the overlapping leaves create natural pinholes, displaying mini eclipses on the ground.
Phenomena associated with eclipses include shadow bands (also known as flying shadows), which are similar to shadows on the bottom of a swimming pool. They occur only just prior to and after totality, when a narrow solar crescent acts as an anisotropic light source.
1919 observations
The observation of a total solar eclipse of May 29, 1919, helped to confirm Einstein's theory of general relativity. By comparing the apparent distance between stars in the constellation Taurus, with and without the Sun between them, Arthur Eddington stated that the theoretical predictions about gravitational lenses were confirmed. The observation with the Sun between the stars was possible only during totality since the stars are then visible. Though Eddington's observations were near the experimental limits of accuracy at the time, work in the later half of the 20th century confirmed his results.
Gravity anomalies
There is a long history of observations of gravity-related phenomena during solar eclipses, especially during the period of totality. In 1954, and again in 1959, Maurice Allais reported observations of strange and unexplained movement during solar eclipses. The reality of this phenomenon, named the Allais effect, has remained controversial. Similarly, in 1970, Saxl and Allen observed the sudden change in motion of a torsion pendulum; this phenomenon is called the Saxl effect.
Observation during the 1997 solar eclipse by Wang et al. suggested a possible gravitational shielding effect, which generated debate. In 2002, Wang and a collaborator published detailed data analysis, which suggested that the phenomenon still remains unexplained.
Eclipses and transits
In principle, the simultaneous occurrence of a solar eclipse and a transit of a planet is possible. But these events are extremely rare because of their short durations. The next anticipated simultaneous occurrence of a solar eclipse and a transit of Mercury will be on July 5, 6757, and a solar eclipse and a transit of Venus is expected on April 5, 15232.
More common, but still infrequent, is a conjunction of a planet (especially, but not only, Mercury or Venus) at the time of a total solar eclipse, in which event the planet will be visible very near the eclipsed Sun, when without the eclipse it would have been lost in the Sun's glare. At one time, some scientists hypothesized that there may be a planet (often given the name Vulcan) even closer to the Sun than Mercury; the only way to confirm its existence would have been to observe it in transit or during a total solar eclipse. No such planet was ever found, and general relativity has since explained the observations that led astronomers to suggest that Vulcan might exist.
Earthshine
During a total solar eclipse, the Moon's shadow covers only a small fraction of the Earth. The Earth continues to receive at least 92 percent of the amount of sunlight it receives without an eclipse – more if the penumbra of the Moon's shadow partly misses the Earth. Seen from the Moon, the Earth during a total solar eclipse is mostly brilliantly illuminated, with only a small dark patch showing the Moon's shadow. The brilliantly lit Earth reflects a lot of light to the Moon. If the corona of the eclipsed Sun were not present, the Moon, illuminated by earthlight, would be easily visible from Earth. This would be essentially the same as the earthshine which can frequently be seen when the Moon's phase is a narrow crescent. In reality, the corona, though much less brilliant than the Sun's photosphere, is much brighter than the Moon illuminated by earthlight. Therefore, by contrast, the Moon during a total solar eclipse appears to be black, with the corona surrounding it.
Artificial satellites
Artificial satellites can also pass in front of the Sun as seen from the Earth, but none is large enough to cause an eclipse. At the altitude of the International Space Station, for example, an object would need to be about 3.35 km (2.08 mi) across to blot the Sun out entirely. These transits are difficult to watch because the zone of visibility is very small. The satellite passes over the face of the Sun in about a second, typically. As with a transit of a planet, it will not get dark.
Observations of eclipses from spacecraft or artificial satellites orbiting above the Earth's atmosphere are not subject to weather conditions. The crew of Gemini 12 observed a total solar eclipse from space in 1966. The partial phase of the 1999 total eclipse was visible from Mir.
During the Apollo–Soyuz Test Project conducted in July 1975, the Apollo spacecraft was positioned to create an artificial solar eclipse giving the Soyuz crew an opportunity to photograph the solar corona.
Impact
The solar eclipse of March 20, 2015, was the first occurrence of an eclipse estimated to potentially have a significant impact on the power system, with the electricity sector taking measures to mitigate any impact. The continental Europe and Great Britain synchronous areas were estimated to have about 90 gigawatts of solar power and it was estimated that production would temporarily decrease by up to 34 GW compared to a clear sky day.
Eclipses may cause the temperature to decrease by 3 °C, with wind power potentially decreasing as winds are reduced by 0.7 m/s.
In addition to the drop in light level and air temperature, animals change their behavior during totality. For example, birds and squirrels return to their nests and crickets chirp.
Recent and forthcoming solar eclipses
Eclipses occur only in the eclipse season, when the Sun is close to either the ascending or descending node of the Moon. Each eclipse is separated by one, five or six lunations (synodic months), and the midpoint of each season is separated by 173.3 days, which is the mean time for the Sun to travel from one node to the next. The period is a little less than half a calendar year because the lunar nodes slowly regress. Because 223 synodic months is roughly equal to 239 anomalistic months and 242 draconic months, eclipses with similar geometry recur 223 synodic months (about 6,585.3 days) apart. This period (18 years 11.3 days) is a saros. Because 223 synodic months is not identical to 239 anomalistic months or 242 draconic months, saros cycles do not endlessly repeat. Each cycle begins with the Moon's shadow crossing the Earth near the north or south pole, and subsequent events progress toward the other pole until the Moon's shadow misses the Earth and the series ends. Saros cycles are numbered; currently, cycles 117 to 156 are active.
| 1997–2000 | 2000–2003 | 2004–2007 | 2008–2011 | 2011–2014 | 2015–2018 | 2018–2021 | 2022–2025 | 2026–2029 |