Neuromuscular junction

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Neuromuscular_junction 

 

Neuromuscular junction
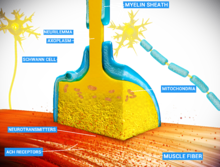
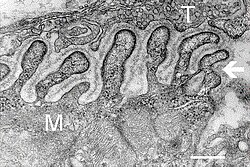Electron micrograph showing a cross section through the neuromuscular junction. T is the axon terminal, M is the muscle fiber. The arrow shows junctional folds with basal lamina. Active zones are visible on the tips between the folds. Scale is 0.3 μm. Source: NIMH
Detailed view of a neuromuscular junction: Presynaptic terminal Sarcolemma Synaptic vesicle Nicotinic acetylcholine receptor Mitochondrion
Details
Identifiers
Latin	synapssis neuromuscularis; junctio neuromuscularis
MeSH	D009469
TH	H2.00.06.1.02001
FMA	61803

At the neuromuscular junction, the nerve fiber is able to transmit a signal to the muscle fiber by releasing ACh (and other substances), causing muscle contraction.

 

Muscles will contract or relax when they receive signals from the nervous system. The neuromuscular junction is the site of the signal exchange. The steps of this process in vertebrates occur as follows:(1) The action potential reaches the axon terminal. (2) Voltage-dependent calcium gates open, allowing calcium to enter the axon terminal. (3) Neurotransmitter vesicles fuse with the presynaptic membrane and ACh is released into the synaptic cleft via exocytosis. (4) ACh binds to postsynaptic receptors on the sarcolemma. (5) This binding causes ion channels to open and allows sodium and other cations to flow across the membrane into the muscle cell. (6) The flow of sodium ions across the membrane into and potassium ions out of the muscle cell generates an action potential which travels to the myofibril and results in muscle contraction.Labels:A: Motor Neuron AxonB: Axon TerminalC. Synaptic CleftD. Muscle CellE. Part of a Myofibril

 

A neuromuscular junction (or myoneural junction) is a chemical synapse between a motor neuron and a muscle fiber. It allows the motor neuron to transmit a signal to the muscle fiber, causing muscle contraction.

Muscles require innervation to function—and even just to maintain muscle tone, avoiding atrophy. In the neuromuscular system nerves from the central nervous system and the peripheral nervous system are linked and work together with muscles. Synaptic transmission at the neuromuscular junction begins when an action potential reaches the presynaptic terminal of a motor neuron, which activates voltage-gated calcium channels to allow calcium ions to enter the neuron. Calcium ions bind to sensor proteins (synaptotagmins) on synaptic vesicles, triggering vesicle fusion with the cell membrane and subsequent neurotransmitter release from the motor neuron into the synaptic cleft. In vertebrates, motor neurons release acetylcholine (ACh), a small molecule neurotransmitter, which diffuses across the synaptic cleft and binds to nicotinic acetylcholine receptors (nAChRs) on the cell membrane of the muscle fiber, also known as the sarcolemma. nAChRs are ionotropic receptors, meaning they serve as ligand-gated ion channels. The binding of ACh to the receptor can depolarize the muscle fiber, causing a cascade that eventually results in muscle contraction.

Neuromuscular junction diseases can be of genetic and autoimmune origin. Genetic disorders, such as Congenital myasthenic syndrome, can arise from mutated structural proteins that comprise the neuromuscular junction, whereas autoimmune diseases, such as myasthenia gravis, occur when antibodies are produced against nicotinic acetylcholine receptors on the sarcolemma.

Structure and function

Motor Endplate

Quantal transmission

At the neuromuscular junction presynaptic motor axons terminate 30 nanometers from the cell membrane or sarcolemma of a muscle fiber. The sarcolemma at the junction has invaginations called postjunctional folds, which increase its surface area facing the synaptic cleft. These postjunctional folds form the motor endplate, which is studded with nicotinic acetylcholine receptors (nAChRs) at a density of 10,000 receptors/micrometer². The presynaptic axons terminate in bulges called terminal boutons (or presynaptic terminals) that project toward the postjunctional folds of the sarcolemma. In the frog each motor nerve terminal contains about 300,000 vesicles, with an average diameter of 0.05 micrometers. The vesicles contain acetylcholine. Some of these vesicles are gathered into groups of fifty, positioned at active zones close to the nerve membrane. Active zones are about 1 micrometer apart. The 30 nanometer cleft between nerve ending and endplate contains a meshwork of acetylcholinesterase (AChE) at a density of 2,600 enzyme molecules/micrometer², held in place by the structural proteins dystrophin and rapsyn. Also present is the receptor tyrosine kinase protein MuSK, a signaling protein involved in the development of the neuromuscular junction, which is also held in place by rapsyn.

About once every second in a resting junction randomly one of the synaptic vesicles fuses with the presynaptic neuron's cell membrane in a process mediated by SNARE proteins. Fusion results in the emptying of the vesicle's contents of 7000–10,000 acetylcholine molecules into the synaptic cleft, a process known as exocytosis. Consequently, exocytosis releases acetylcholine in packets that are called quanta. The acetylcholine quantum diffuses through the acetylcholinesterase meshwork, where the high local transmitter concentration occupies all of the binding sites on the enzyme in its path. The acetylcholine that reaches the endplate activates ~2,000 acetylcholine receptors, opening their ion channels which permits sodium ions to move into the endplate producing a depolarization of ~0.5 mV known as a miniature endplate potential (MEPP). By the time the acetylcholine is released from the receptors the acetylcholinesterase has destroyed its bound ACh, which takes about ~0.16 ms, and hence is available to destroy the ACh released from the receptors.

When the motor nerve is stimulated there is a delay of only 0.5 to 0.8 msec between the arrival of the nerve impulse in the motor nerve terminals and the first response of the endplate  The arrival of the motor nerve action potential at the presynaptic neuron terminal opens voltage-dependent calcium channels and Ca²⁺ ions flow from the extracellular fluid into the presynaptic neuron's cytosol. This influx of Ca²⁺ causes several hundred neurotransmitter-containing vesicles to fuse with the presynaptic neuron's cell membrane through SNARE proteins to release their acetylcholine quanta by exocytosis. The endplate depolarization by the released acetylcholine is called an endplate potential (EPP). The EPP is accomplished when ACh binds the nicotinic acetylcholine receptors (nAChR) at the motor end plate, and causes an influx of sodium ions. This influx of sodium ions generates the EPP (depolarization), and triggers an action potential that travels along the sarcolemma and into the muscle fiber via the T-tubules (transverse tubules) by means of voltage-gated sodium channels. The conduction of action potentials along the T-tubules stimulates the opening of voltage-gated Ca²⁺ channels which are mechanically coupled to Ca²⁺ release channels in the sarcoplasmic reticulum. The Ca²⁺ then diffuses out of the sarcoplasmic reticulum to the myofibrils so it can stimulate contraction. The endplate potential is thus responsible for setting up an action potential in the muscle fiber which triggers muscle contraction. The transmission from nerve to muscle is so rapid because each quantum of acetylcholine reaches the endplate in millimolar concentrations, high enough to combine with a receptor with a low affinity, which then swiftly releases the bound transmitter.

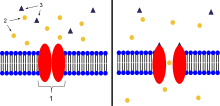
Acetylcholine receptors

1. Ion channel linked receptor
2. Ions
3. Ligand (such as acetylcholine)

When ligands bind to the receptor, the ion channel portion of the receptor opens, allowing ions to pass across the cell membrane.

Acetylcholine is a neurotransmitter synthesized from dietary choline and acetyl-CoA (ACoA), and is involved in the stimulation of muscle tissue in vertebrates as well as in some invertebrate animals. In vertebrates, the acetylcholine receptor subtype that is found at the neuromuscular junction of skeletal muscles is the nicotinic acetylcholine receptor (nAChR), which is a ligand-gated ion channel. Each subunit of this receptor has a characteristic "cys-loop", which is composed of a cysteine residue followed by 13 amino acid residues and another cysteine residue. The two cysteine residues form a disulfide linkage which results in the "cys-loop" receptor that is capable of binding acetylcholine and other ligands. These cys-loop receptors are found only in eukaryotes, but prokaryotes possess ACh receptors with similar properties. Not all species use a cholinergic neuromuscular junction; e.g. crayfish and fruit flies have a glutamatergic neuromuscular junction.

AChRs at the skeletal neuromuscular junction form heteropentamers composed of two α, one β, one ɛ, and one δ subunits. When a single ACh ligand binds to one of the α subunits of the ACh receptor it induces a conformational change at the interface with the second AChR α subunit. This conformational change results in the increased affinity of the second α subunit for a second ACh ligand. AChRs, therefore, exhibit a sigmoidal dissociation curve due to this cooperative binding. The presence of the inactive, intermediate receptor structure with a single-bound ligand keeps ACh in the synapse that might otherwise be lost by cholinesterase hydrolysis or diffusion. The persistence of these ACh ligands in the synapse can cause a prolonged post-synaptic response.

Development

The development of the neuromuscular junction requires signaling from both the motor neuron's terminal and the muscle cell's central region. During development, muscle cells produce acetylcholine receptors (AChRs) and express them in the central regions in a process called prepatterning. Agrin, a heparin proteoglycan, and MuSK kinase are thought to help stabilize the accumulation of AChR in the central regions of the myocyte. MuSK is a receptor tyrosine kinase—meaning that it induces cellular signaling by binding phosphate molecules to self regions like tyrosines, and to other targets in the cytoplasm. Upon activation by its ligand agrin, MuSK signals via two proteins called "Dok-7" and "rapsyn", to induce "clustering" of acetylcholine receptors. ACh release by developing motor neurons produces postsynaptic potentials in the muscle cell that positively reinforces the localization and stabilization of the developing neuromuscular junction.

These findings were demonstrated in part by mouse "knockout" studies. In mice which are deficient for either agrin or MuSK, the neuromuscular junction does not form. Further, mice deficient in Dok-7 did not form either acetylcholine receptor clusters or neuromuscular synapses.

The development of neuromuscular junctions is mostly studied in model organisms, such as rodents. In addition, in 2015 an all-human neuromuscular junction has been created in vitro using human embryonic stem cells and somatic muscle stem cells. In this model presynaptic motor neurons are activated by optogenetics and in response synaptically connected muscle fibers twitch upon light stimulation.

Research methods

José del Castillo and Bernard Katz used ionophoresis to determine the location and density of nicotinic acetylcholine receptors (nAChRs) at the neuromuscular junction. With this technique, a microelectrode was placed inside the motor endplate of the muscle fiber, and a micropipette filled with acetylcholine (ACh) is placed directly in front of the endplate in the synaptic cleft. A positive voltage was applied to the tip of the micropipette, which caused a burst of positively charged ACh molecules to be released from the pipette. These ligands flowed into the space representing the synaptic cleft and bound to AChRs. The intracellular microelectrode monitored the amplitude of the depolarization of the motor endplate in response to ACh binding to nicotinic (ionotropic) receptors. Katz and del Castillo showed that the amplitude of the depolarization (excitatory postsynaptic potential) depended on the proximity of the micropipette releasing the ACh ions to the endplate. The farther the micropipette was from the motor endplate, the smaller the depolarization was in the muscle fiber. This allowed the researchers to determine that the nicotinic receptors were localized to the motor endplate in high density.

Toxins are also used to determine the location of acetylcholine receptors at the neuromuscular junction. α-Bungarotoxin is a toxin found in the snake species Bungarus multicinctus that acts as an ACh antagonist and binds to AChRs irreversibly. By coupling assayable enzymes such as horseradish peroxidase (HRP) or fluorescent proteins such as green fluorescent protein (GFP) to the α-bungarotoxin, AChRs can be visualized and quantified.

Toxins that affect the neuromuscular junction

Nerve gases

Nerve gases bind to and phosphorylate AChE, effectively deactivating them. The accumulation of ACh within the synaptic cleft causes muscle cells to be perpetually contracted, leading to severe complications such as paralysis and death within minutes of exposure.

Botulinum toxin injected in human face

Botulinum toxin

Botulinum toxin (also known as botulinum neurotoxin, and commercially sold under the trade name Botox) inhibits the release of acetylcholine at the neuromuscular junction by interfering with SNARE proteins. This toxin crosses into the nerve terminal through the process of endocytosis and subsequently cleaves SNARE proteins, preventing the ACh vesicles from fusing with the intracellular membrane. This induces a transient flaccid paralysis and chemical denervation localized to the striated muscle that it has affected. The inhibition of ACh release does not set in until approximately two weeks after the injection is made. Three months after the inhibition occurs, neuronal activity begins to regain partial function, and six months after, complete neuronal function is regained.

Tetanus toxin

Tetanus toxin, also known as tetanospasmin is a potent neurotoxin produced by Clostridium tetani and causes the disease state, tetanus. The LD₅₀ of this toxin has been measured to be approximately 1 ng/kg, making it second only to botulinum toxin D as the deadliest toxin in the world. It functions very similarly to botulinum neurotoxin by attaching and endocytosing into the presynaptic nerve terminal and interfering with SNARE proteins. It differs from botulinum neurotoxin in a few ways, most apparently in its end state, wherein tetanospasmin causes spastic paralysis as opposed to the flaccid paralysis demonstrated with botulinum neurotoxin.

Latrotoxin

Latrotoxin (α-Latrotoxin) found in venom of widow spiders also affects the neuromuscular junction by causing the release of acetylcholine from the presynaptic cell. Mechanisms of action include binding to receptors on the presynaptic cell activating the IP3/DAG pathway and release of calcium from intracellular stores and pore formation resulting in influx of calcium ions directly. Either mechanism causes increased calcium in presynaptic cell, which then leads to release of synaptic vesicles of acetylcholine. Latrotoxin causes pain, muscle contraction and if untreated potentially paralysis and death.

Snake venom

Snake venoms act as toxins at the neuromuscular junction and can induce weakness and paralysis. Venoms can act as both presynaptic and postsynaptic neurotoxins.

Presynaptic neurotoxins, commonly known as β-neurotoxins, affect the presynaptic regions of the neuromuscular junction. The majority of these neurotoxins act by inhibiting the release of neurotransmitters, such as acetylcholine, into the synapse between neurons. However, some of these toxins have also been known to enhance neurotransmitter release. Those that inhibit neurotransmitter release create a neuromuscular blockade that prevents signaling molecules from reaching their postsynaptic target receptors. In doing so, the victim of these snake bite suffer from profound weakness. Such neurotoxins do not respond well to anti-venoms. After one hour of inoculation of these toxins, including notexin and taipoxin, many of the affected nerve terminals show signs of irreversible physical damage, leaving them devoid of any synaptic vesicles.

Postsynaptic neurotoxins, otherwise known as α-neurotoxins, act oppositely to the presynaptic neurotoxins by binding to the postsynaptic acetylcholine receptors. This prevents interaction between the acetylcholine released by the presynaptic terminal and the receptors on the postsynaptic cell. In effect, the opening of sodium channels associated with these acetylcholine receptors is prohibited, resulting in a neuromuscular blockade, similar to the effects seen due to presynaptic neurotoxins. This causes paralysis in the muscles involved in the affected junctions. Unlike presynaptic neurotoxins, postsynaptic toxins are more easily affected by anti-venoms, which accelerate the dissociation of the toxin from the receptors, ultimately causing a reversal of paralysis. These neurotoxins experimentally and qualitatively aid in the study of acetylcholine receptor density and turnover, as well as in studies observing the direction of antibodies toward the affected acetylcholine receptors in patients diagnosed with myasthenia gravis.

Diseases

Main article: Neuromuscular junction disease

Any disorder that compromises the synaptic transmission between a motor neuron and a muscle cell is categorized under the umbrella term of neuromuscular diseases. These disorders can be inherited or acquired and can vary in their severity and mortality. In general, most of these disorders tend to be caused by mutations or autoimmune disorders. Autoimmune disorders, in the case of neuromuscular diseases, tend to be humoral mediated, B cell mediated, and result in an antibody improperly created against a motor neuron or muscle fiber protein that interferes with synaptic transmission or signaling.

Autoimmune

Myasthenia gravis

Myasthenia gravis is an autoimmune disorder where the body makes antibodies against either the acetylcholine receptor (AchR) (in 80% of cases), or against postsynaptic muscle-specific kinase (MuSK) (0–10% of cases). In seronegative myasthenia gravis low density lipoprotein receptor-related protein 4 is targeted by IgG1, which acts as a competitive inhibitor of its ligand, preventing the ligand from binding its receptor. It is not known if seronegative myasthenia gravis will respond to standard therapies.

Neonatal MG

Neonatal MG is an autoimmune disorder that affects 1 in 8 children born to mothers who have been diagnosed with myasthenia gravis (MG). MG can be transferred from the mother to the fetus by the movement of AChR antibodies through the placenta. Signs of this disease at birth include weakness, which responds to anticholinesterase medications, as well as fetal akinesia, or the lack of fetal movement. This form of the disease is transient, lasting for about three months. However, in some cases, neonatal MG can lead to other health effects, such as arthrogryposis and even fetal death. These conditions are thought to be initiated when maternal AChR antibodies are directed to the fetal AChR and can last until the 33rd week of gestation, when the γ subunit of AChR is replaced by the ε subunit.

Lambert-Eaton myasthenic syndrome

Lambert–Eaton myasthenic syndrome (LEMS) is an autoimmune disorder that affects the presynaptic portion of the neuromuscular junction. This rare disease can be marked by a unique triad of symptoms: proximal muscle weakness, autonomic dysfunction, and areflexia. Proximal muscle weakness is a product of pathogenic autoantibodies directed against P/Q-type voltage-gated calcium channels, which in turn leads to a reduction of acetylcholine release from motor nerve terminals on the presynaptic cell. Examples of autonomic dysfunction caused by LEMS include erectile dysfunction in men, constipation, and, most commonly, dry mouth. Less common dysfunctions include dry eyes and altered perspiration. Areflexia is a condition in which tendon reflexes are reduced and it may subside temporarily after a period of exercise.

50–60% of the patients that are diagnosed with LEMS also have present an associated tumor, which is typically small-cell lung carcinoma (SCLC). This type of tumor also expresses voltage-gated calcium channels. Oftentimes, LEMS also occurs alongside myasthenia gravis.

Treatment for LEMS consists of using 3,4-diaminopyridine as a first measure, which serves to increase the compound muscle action potential as well as muscle strength by lengthening the time that voltage-gated calcium channels remain open after blocking voltage-gated potassium channels. In the US, treatment with 3,4-diaminopyridine for eligible LEMS patients is available at no cost under an expanded access program. Further treatment includes the use of prednisone and azathioprine in the event that 3,4-diaminopyridine does not aid in treatment.

Neuromyotonia

Neuromyotonia (NMT), otherwise known as Isaac's syndrome, is unlike many other diseases present at the neuromuscular junction. Rather than causing muscle weakness, NMT leads to the hyperexcitation of motor nerves. NMT causes this hyperexcitation by producing longer depolarizations by down-regulating voltage-gated potassium channels, which causes greater neurotransmitter release and repetitive firing. This increase in rate of firing leads to more active transmission and as a result, greater muscular activity in the affected individual. NMT is also believed to be of autoimmune origin due to its associations with autoimmune symptoms in the individual affected.

Genetic

Congenital myasthenic syndromes

Congenital myasthenic syndromes (CMS) are very similar to both MG and LEMS in their functions, but the primary difference between CMS and those diseases is that CMS is of genetic origins. Specifically, these syndromes are diseases incurred due to mutations, typically recessive, in 1 of at least 10 genes that affect presynaptic, synaptic, and postsynaptic proteins in the neuromuscular junction. Such mutations usually arise in the ε-subunit of AChR, thereby affecting the kinetics and expression of the receptor itself. Single nucleotide substitutions or deletions may cause loss of function in the subunit. Other mutations, such as those affecting acetylcholinesterase and acetyltransferase, can also cause the expression of CMS, with the latter being associated specifically with episodic apnea. These syndromes can present themselves at different times within the life of an individual. They may arise during the fetal phase, causing fetal akinesia, or the perinatal period, during which certain conditions, such as arthrogryposis, ptosis, hypotonia, ophthalmoplegia, and feeding or breathing difficulties, may be observed. They could also activate during adolescence or adult years, causing the individual to develop slow-channel syndrome.

Treatment for particular subtypes of CMS (postsynaptic fast-channel CMS) is similar to treatment for other neuromuscular disorders. 3,4-Diaminopyridine, the first-line treatment for LEMS, is under development as an orphan drug for CMS in the US, and available to eligible patients under an expanded access program at no cost.

Meno

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Meno

Meno (/ˈmiːnoʊ/; Greek: Μένων, Ménōn) is a Socratic dialogue by Plato. Meno begins the dialogue by asking Socrates whether virtue is taught, acquired by practice, or comes by nature. In order to determine whether virtue is teachable or not, Socrates tells Meno that they first need to determine what virtue is. When the characters speak of virtue, or rather arete, they refer to virtue in general, rather than particular virtues, such as justice or temperance. The first part of the work showcases Socratic dialectical style; Meno, unable to adequately define virtue, is reduced to confusion or aporia. Socrates suggests that they seek an adequate definition for virtue together. In response, Meno suggests that it is impossible to seek what one does not know, because one will be unable to determine whether one has found it.

Socrates challenges Meno's argument, often called "Meno's Paradox" or the "Learner's Paradox", by introducing the theory of knowledge as recollection (anamnesis). As presented in the dialogue, the theory proposes that souls are immortal and know all things in a disembodied state; learning in the embodied is actually a process of recollecting that which the soul knew before it came into a body. Socrates demonstrates recollection in action by posing a mathematical puzzle to one of Meno's slaves. Subsequently, Socrates and Meno return to the question of whether virtue is teachable, employing the method of hypothesis. Near the end of the dialogue, Meno poses another famous puzzle, called "The Meno Problem" or "The Value Problem for Knowledge", which questions why knowledge is valued more highly than true belief. In response, Socrates provides a famous and somewhat enigmatic distinction between knowledge and true belief.

Characters

Plato's Meno is a Socratic dialogue in which the two main speakers, Socrates and Meno (also transliterated as "Menon"), discuss human virtue: what it is, and whether or not it can be taught. Meno is visiting Athens from Thessaly with a large entourage of slaves attending him. Young, good-looking and well-born, he is a student of Gorgias, a prominent sophist whose views on virtue clearly influence that of Meno's. Early in the dialogue, Meno claims that he has held forth many times on the subject of virtue, and in front of large audiences.

One of Meno's slaves also has a speaking role, as one of the features of the dialogue is Socrates' use of the slave to demonstrate his idea of anamnesis: certain knowledge is innate and "recollected" by the soul through proper inquiry.

Another participant in the dialogue is Athenian politician Anytus, a prosecutor of Socrates with whom Meno is friendly.

Dialogue

Introduction of virtue

The dialogue begins with Meno asking Socrates to tell him if virtue can be taught. Socrates says that he does not know what virtue is, and neither does anyone else he knows. Meno responds that, according to Gorgias, virtue is different for different people, that what is virtuous for a man is to conduct himself in the city so that he helps his friends, injures his enemies, and takes care all the while that he personally comes to no harm. Virtue is different for a woman, he says. Her domain is the management of the household, and she is supposed to obey her husband. He says that children (male and female) have their own proper virtue, and so do old men—free or slaves. Socrates objects: there must be some virtue common to all human beings.

Socrates rejects the idea that human virtue depends on a person's sex or age. He leads Meno towards the idea that virtues are common to all people, that sophrosunê ('temperance', i.e. exercise of self-control) and dikê (aka dikaiosunê; 'justice', i.e. refrain from harming others) are virtues even in children and old men. Meno proposes to Socrates that the "capacity to govern men" may be a virtue common to all people. Socrates points out to the slaveholder that "governing well" cannot be a virtue of a slave, because then he would not be a slave.

One of the errors that Socrates points out is that Meno lists many particular virtues without defining a common feature inherent to virtues which makes them thus. Socrates remarks that Meno makes many out of one, like somebody who breaks a plate.

Meno proposes that virtue is the desire for good things and the power to get them. Socrates points out that this raises a second problem—many people do not recognize evil. The discussion then turns to the question of accounting for the fact that so many people are mistaken about good and evil and take one for the other. Socrates asks Meno to consider whether good things must be acquired virtuously in order to be really good. Socrates leads onto the question of whether virtue is one thing or many.

No satisfactory definition of virtue emerges in the Meno. Socrates' comments, however, show that he considers a successful definition to be unitary, rather than a list of varieties of virtue, that it must contain all and only those terms which are genuine instances of virtue, and must not be circular.

Meno's paradox

Meno asks Socrates:

And how will you enquire, Socrates, into that which you do not know? What will you put forth as the subject of enquiry? And if you find what you want, how will you ever know that this is the thing which you did not know?

Socrates rephrases the question, which has come to be the canonical statement of the paradox:

[A] man cannot enquire either about that which he knows, or about that which he does not know; for if he knows, he has no need to enquire; and if not, he cannot; for he does not know the very subject about which he is to enquire.

— translated by Benjamin Jowett, 1871

Dialogue with Meno's slave

Socrates responds to this sophistical paradox with a mythos ('narrative' or 'fiction') according to which souls are immortal and have learned everything prior to transmigrating into the human body. Since the soul has had contact with real things prior to birth, we have only to 'recollect' them when alive. Such recollection requires Socratic questioning, which according to Socrates is not teaching. Socrates demonstrates his method of questioning and recollection by interrogating a slave who is ignorant of geometry.

Socrates begins one of the most influential dialogues of Western philosophy regarding the argument for inborn knowledge. By drawing geometric figures in the ground Socrates demonstrates that the slave is initially unaware of the length that a side must be in order to double the area of a square with 2-foot sides. The slave guesses first that the original side must be doubled in length (4 feet), and when this proves too much, that it must be 3 feet. This is still too much, and the slave is at a loss.

Socrates claims that before he got hold of him the slave (who has been picked at random from Meno's entourage) might have thought he could speak "well and fluently" on the subject of a square double the size of a given square. Socrates comments that this "numbing" he caused in the slave has done him no harm and has even benefited him.

The blue square is twice the area of the yellow square

Socrates then adds three more squares to the original square, to form a larger square four times the size. He draws four diagonal lines which bisect each of the smaller squares. Through questioning, Socrates leads the slave to the discovery that the square formed by these diagonals has an area of eight square feet, double that of the original. He says that the slave has "spontaneously recovered" knowledge he knew from a past life without having been taught. Socrates is satisfied that new beliefs were "newly aroused" in the slave.

After witnessing the example with the slave boy, Meno tells Socrates that he thinks that Socrates is correct in his theory of recollection, to which Socrates agrees:

Some things I have said of which I am not altogether confident. But that we shall be better and braver and less helpless if we think that we ought to enquire, than we should have been if we indulged in the idle fancy that there was no knowing and no use in seeking to know what we do not know; that is a theme upon which I am ready to fight, in word and deed, to the utmost of my power.

— translated by Benjamin Jowett, 1871

Anytus

Meno now beseeches Socrates to return to the original question, how virtue is acquired, and in particular, whether or not it is acquired by teaching or through life experience. Socrates proceeds on the hypothesis that virtue is knowledge, and it is quickly agreed that, if this is true, virtue is teachable. They turn to the question of whether virtue is indeed knowledge. Socrates is hesitant, because, if virtue were knowledge, there should be teachers and learners of it, but there are none.

Coincidentally Anytus appears, whom Socrates praises as the son of Anthemion, who earned his fortune with intelligence and hard work. He says that Anthemion had his son well-educated and so Anytus is well-suited to join the investigation. Socrates suggests that the sophists are teachers of virtue. Anytus is horrified, saying that he neither knows any, nor cares to know any. Socrates then questions why it is that men do not always produce sons of the same virtue as themselves. He alludes to other notable male figures, such as Themistocles, Aristides, Pericles and Thucydides, and casts doubt on whether these men produced sons as capable of virtue as themselves. Anytus becomes offended and accuses Socrates of slander, warning him to be careful expressing such opinions. (The historical Anytus was one of Socrates' accusers in his trial.) Socrates suggests that Anytus does not realize what slander is, and continues his dialogue with Meno as to the definition of virtue.

True belief and knowledge

After the discussion with Anytus, Socrates returns to quizzing Meno for his own thoughts on whether the sophists are teachers of virtue and whether virtue can be taught. Meno is again at a loss, and Socrates suggests that they have made a mistake in agreeing that knowledge is required for virtue. He points out the similarities and differences between "true belief" and "knowledge". True beliefs are as useful to us as knowledge, but they often fail to "stay in their place" and must be "tethered" by what he calls aitias logismos ('calculation of reason' or 'reasoned explanation'), immediately adding that this is anamnesis, or recollection.

Whether or not Plato intends that the tethering of true beliefs with reasoned explanations must always involve anamnesis is explored in later interpretations of the text. Socrates' distinction between "true belief" and "knowledge" forms the basis of the philosophical definition of knowledge as "justified true belief". Myles Burnyeat and others, however, have argued that the phrase aitias logismos refers to a practical working out of a solution, rather than a justification.

Socrates concludes that, in the virtuous people of the present and the past, at least, virtue has been the result of divine inspiration, akin to the inspiration of the poets, whereas a knowledge of it will require answering the basic question, what is virtue?. In most modern readings these closing remarks are "evidently ironic", but Socrates' invocation of the gods may be sincere, albeit "highly tentative".

This passage in the Meno is often seen as the first statement of the problem of the value of knowledge: how is knowledge more valuable than mere true belief? The nature of knowledge and belief is also discussed in the Thaetetus.

Meno and Protagoras

Meno's theme is also dealt with in the dialogue Protagoras, where Plato ultimately has Socrates arrive at the opposite conclusion: virtue can be taught. Likewise, while in Protagoras knowledge is uncompromisingly this-worldly, in Meno the theory of recollection points to a link between knowledge and eternal truths.

Texts and translations

• Meno, in a collection of Plato's Dialogues at Standard Ebooks
• Jowett, Benjamin. 1871. "Meno." – via Internet Classics Archive. Project Gutenberg: 1643.
• Lamb, W. R. M., trans. [1924] 1967. "Meno." Plato in Twelve Volumes 3. Cambridge, MA, Harvard University Press. ISBN 0-674-99183-4, 0-674-99184-2. – via Perseus Project.
• Woods, Cathal, trans. 2011. "Meno." SSRN 1910945.

Recursion

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Recursion

 

A visual form of recursion known as the Droste effect. The woman in this image holds an object that contains a smaller image of her holding an identical object, which in turn contains a smaller image of herself holding an identical object, and so forth. 1904 Droste cocoa tin, designed by Jan Misset

Recursion occurs when the definition of a concept or process depends on a simpler version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no infinite loop or infinite chain of references can occur.

A process that exhibits recursion is recursive.

Formal definitions

Ouroboros, an ancient symbol depicting a serpent or dragon eating its own tail

In mathematics and computer science, a class of objects or methods exhibits recursive behavior when it can be defined by two properties:

• A simple base case (or cases) — a terminating scenario that does not use recursion to produce an answer
• A recursive step — a set of rules that reduces all successive cases toward the base case.

For example, the following is a recursive definition of a person's ancestor. One's ancestor is either:

• One's parent (base case), or
• One's parent's ancestor (recursive step).

The Fibonacci sequence is another classic example of recursion:

Fib(0) = 0 as base case 1,

Fib(1) = 1 as base case 2,

For all integers n > 1, Fib(n) = Fib(n − 1) + Fib(n − 2).

Many mathematical axioms are based upon recursive rules. For example, the formal definition of the natural numbers by the Peano axioms can be described as: "Zero is a natural number, and each natural number has a successor, which is also a natural number." By this base case and recursive rule, one can generate the set of all natural numbers.

Other recursively defined mathematical objects include factorials, functions (e.g., recurrence relations), sets (e.g., Cantor ternary set), and fractals.

There are various more tongue-in-cheek definitions of recursion; see recursive humor.

Informal definition

Recently refreshed sourdough, bubbling through fermentation: the recipe calls for some sourdough left over from the last time the same recipe was made.

Recursion is the process a procedure goes through when one of the steps of the procedure involves invoking the procedure itself. A procedure that goes through recursion is said to be 'recursive'.

To understand recursion, one must recognize the distinction between a procedure and the running of a procedure. A procedure is a set of steps based on a set of rules, while the running of a procedure involves actually following the rules and performing the steps.

Recursion is related to, but not the same as, a reference within the specification of a procedure to the execution of some other procedure.

When a procedure is defined as such, this immediately creates the possibility of an endless loop; recursion can only be properly used in a definition if the step in question is skipped in certain cases so that the procedure can complete.

But even if it is properly defined, a recursive procedure is not easy for humans to perform, as it requires distinguishing the new from the old, partially executed invocation of the procedure; this requires some administration as to how far various simultaneous instances of the procedures have progressed. For this reason, recursive definitions are very rare in everyday situations.

In language

Linguist Noam Chomsky, among many others, has argued that the lack of an upper bound on the number of grammatical sentences in a language, and the lack of an upper bound on grammatical sentence length (beyond practical constraints such as the time available to utter one), can be explained as the consequence of recursion in natural language.

This can be understood in terms of a recursive definition of a syntactic category, such as a sentence. A sentence can have a structure in which what follows the verb is another sentence: Dorothy thinks witches are dangerous, in which the sentence witches are dangerous occurs in the larger one. So a sentence can be defined recursively (very roughly) as something with a structure that includes a noun phrase, a verb, and optionally another sentence. This is really just a special case of the mathematical definition of recursion.

This provides a way of understanding the creativity of language—the unbounded number of grammatical sentences—because it immediately predicts that sentences can be of arbitrary length: Dorothy thinks that Toto suspects that Tin Man said that.... There are many structures apart from sentences that can be defined recursively, and therefore many ways in which a sentence can embed instances of one category inside another. Over the years, languages in general have proved amenable to this kind of analysis.

The generally accepted idea that recursion is an essential property of human language has been challenged by Daniel Everett on the basis of his claims about the Pirahã language. Andrew Nevins, David Pesetsky and Cilene Rodrigues are among many who have argued against this. Literary self-reference can in any case be argued to be different in kind from mathematical or logical recursion.

Recursion plays a crucial role not only in syntax, but also in natural language semantics. The word and, for example, can be construed as a function that can apply to sentence meanings to create new sentences, and likewise for noun phrase meanings, verb phrase meanings, and others. It can also apply to intransitive verbs, transitive verbs, or ditransitive verbs. In order to provide a single denotation for it that is suitably flexible, and is typically defined so that it can take any of these different types of meanings as arguments. This can be done by defining it for a simple case in which it combines sentences, and then defining the other cases recursively in terms of the simple one.

A recursive grammar is a formal grammar that contains recursive production rules.

Recursive humor

Recursion is sometimes used humorously in computer science, programming, philosophy, or mathematics textbooks, generally by giving a circular definition or self-reference, in which the putative recursive step does not get closer to a base case, but instead leads to an infinite regress. It is not unusual for such books to include a joke entry in their glossary along the lines of:

Recursion, see Recursion.

A variation is found on page 269 in the index of some editions of Brian Kernighan and Dennis Ritchie's book The C Programming Language; the index entry recursively references itself ("recursion 86, 139, 141, 182, 202, 269"). Early versions of this joke can be found in Let's talk Lisp by Laurent Siklóssy (published by Prentice Hall PTR on December 1, 1975, with a copyright date of 1976) and in Software Tools by Kernighan and Plauger (published by Addison-Wesley Professional on January 11, 1976). The joke also appears in The UNIX Programming Environment by Kernighan and Pike. It did not appear in the first edition of The C Programming Language. The joke is part of the Functional programming folklore and was already widespread in the functional programming community before the publication of the aforementioned books.

A plaque commemorates the Toronto Recursive History Project of Toronto's Recursive History.

Another joke is that "To understand recursion, you must understand recursion." In the English-language version of the Google web search engine, when a search for "recursion" is made, the site suggests "Did you mean: recursion." An alternative form is the following, from Andrew Plotkin: "If you already know what recursion is, just remember the answer. Otherwise, find someone who is standing closer to Douglas Hofstadter than you are; then ask him or her what recursion is."

Recursive acronyms are other examples of recursive humor. PHP, for example, stands for "PHP Hypertext Preprocessor", WINE stands for "WINE Is Not an Emulator", GNU stands for "GNU's not Unix", and SPARQL denotes the "SPARQL Protocol and RDF Query Language".

In mathematics

The Sierpinski triangle—a confined recursion of triangles that form a fractal

Recursively defined sets

Main article: Recursive definition

Example: the natural numbers

See also: Closure (mathematics)

The canonical example of a recursively defined set is given by the natural numbers:

0 is in ${\displaystyle \mathbb{N}}$

if n is in ${\displaystyle \mathbb{N}}$, then n + 1 is in ${\displaystyle \mathbb{N}}$

The set of natural numbers is the smallest set satisfying the previous two properties.

In mathematical logic, the Peano axioms (or Peano postulates or Dedekind–Peano axioms), are axioms for the natural numbers presented in the 19th century by the German mathematician Richard Dedekind and by the Italian mathematician Giuseppe Peano. The Peano Axioms define the natural numbers referring to a recursive successor function and addition and multiplication as recursive functions.

Example: Proof procedure

Another interesting example is the set of all "provable" propositions in an axiomatic system that are defined in terms of a proof procedure which is inductively (or recursively) defined as follows:

• If a proposition is an axiom, it is a provable proposition.
• If a proposition can be derived from true reachable propositions by means of inference rules, it is a provable proposition.
• The set of provable propositions is the smallest set of propositions satisfying these conditions.

Finite subdivision rules

Main article: Finite subdivision rule

Finite subdivision rules are a geometric form of recursion, which can be used to create fractal-like images. A subdivision rule starts with a collection of polygons labelled by finitely many labels, and then each polygon is subdivided into smaller labelled polygons in a way that depends only on the labels of the original polygon. This process can be iterated. The standard `middle thirds' technique for creating the Cantor set is a subdivision rule, as is barycentric subdivision.

Functional recursion

A function may be recursively defined in terms of itself. A familiar example is the Fibonacci number sequence: F(n) = F(n − 1) + F(n − 2). For such a definition to be useful, it must be reducible to non-recursively defined values: in this case F(0) = 0 and F(1) = 1.

A famous recursive function is the Ackermann function, which, unlike the Fibonacci sequence, cannot be expressed without recursion.

Proofs involving recursive definitions

Applying the standard technique of proof by cases to recursively defined sets or functions, as in the preceding sections, yields structural induction — a powerful generalization of mathematical induction widely used to derive proofs in mathematical logic and computer science.

Recursive optimization

Dynamic programming is an approach to optimization that restates a multiperiod or multistep optimization problem in recursive form. The key result in dynamic programming is the Bellman equation, which writes the value of the optimization problem at an earlier time (or earlier step) in terms of its value at a later time (or later step).

The recursion theorem

In set theory, this is a theorem guaranteeing that recursively defined functions exist. Given a set X, an element a of X and a function f: X → X, the theorem states that there is a unique function ${\displaystyle F:\mathbb{N}\to X}$ (where ${\displaystyle \mathbb{N}}$ denotes the set of natural numbers including zero) such that

${\displaystyle F(0)=a}$

${\displaystyle F(n+1)=f(F(n))}$

for any natural number n.

Proof of uniqueness

Take two functions ${\displaystyle F:\mathbb{N}\to X}$ and ${\displaystyle G:\mathbb{N}\to X}$ such that:

${\displaystyle F(0)=a}$

${\displaystyle G(0)=a}$

${\displaystyle F(n+1)=f(F(n))}$

${\displaystyle G(n+1)=f(G(n))}$

where a is an element of X.

It can be proved by mathematical induction that F(n) = G(n) for all natural numbers n:

Base Case: F(0) = a = G(0) so the equality holds for n = 0.

Inductive Step: Suppose F(k) = G(k) for some ${\displaystyle k\in \mathbb{N}}$. Then F(k + 1) = f(F(k)) = f(G(k)) = G(k + 1).

Hence F(k) = G(k) implies F(k + 1) = G(k + 1).

By induction, F(n) = G(n) for all ${\displaystyle n\in \mathbb{N}}$.

In computer science

Main article: Recursion (computer science)

A common method of simplification is to divide a problem into subproblems of the same type. As a computer programming technique, this is called divide and conquer and is key to the design of many important algorithms. Divide and conquer serves as a top-down approach to problem solving, where problems are solved by solving smaller and smaller instances. A contrary approach is dynamic programming. This approach serves as a bottom-up approach, where problems are solved by solving larger and larger instances, until the desired size is reached.

A classic example of recursion is the definition of the factorial function, given here in Python code:

def factorial(n):
    if n > 0:
        return n * factorial(n - 1)
    else:
        return 1

The function calls itself recursively on a smaller version of the input (n - 1) and multiplies the result of the recursive call by n, until reaching the base case, analogously to the mathematical definition of factorial.

Recursion in computer programming is exemplified when a function is defined in terms of simpler, often smaller versions of itself. The solution to the problem is then devised by combining the solutions obtained from the simpler versions of the problem. One example application of recursion is in parsers for programming languages. The great advantage of recursion is that an infinite set of possible sentences, designs or other data can be defined, parsed or produced by a finite computer program.

Recurrence relations are equations which define one or more sequences recursively. Some specific kinds of recurrence relation can be "solved" to obtain a non-recursive definition (e.g., a closed-form expression).

Use of recursion in an algorithm has both advantages and disadvantages. The main advantage is usually the simplicity of instructions. The main disadvantage is that the memory usage of recursive algorithms may grow very quickly, rendering them impractical for larger instances.

In biology

Shapes that seem to have been created by recursive processes sometimes appear in plants and animals, such as in branching structures in which one large part branches out into two or more similar smaller parts. One example is Romanesco broccoli.

In business

Further information: Management cybernetics

Recursion is sometimes referred to in management science as the process of iterating through levels of abstraction in large business entities. A common example is the recursive nature of management hierarchies, ranging from line management to senior management via middle management. It also encompasses the larger issue of capital structure in corporate governance.

In art

Recursive dolls: the original set of Matryoshka dolls by Zvyozdochkin and Malyutin, 1892

 

Front face of Giotto's Stefaneschi Triptych, 1320, recursively contains an image of itself (held up by the kneeling figure in the central panel).

 

See also: Mathematics and art and Infinity mirror

The Russian Doll or Matryoshka doll is a physical artistic example of the recursive concept.

Recursion has been used in paintings since Giotto's Stefaneschi Triptych, made in 1320. Its central panel contains the kneeling figure of Cardinal Stefaneschi, holding up the triptych itself as an offering. This practice is more generally known as the Droste effect, an example of the Mise en abyme technique.

M. C. Escher's Print Gallery (1956) is a print which depicts a distorted city containing a gallery which recursively contains the picture, and so ad infinitum.

In culture

The film Inception has colloquialized the appending of the suffix -ception to a noun to jokingly indicate the recursion of something.

Muscle weakness

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Muscle_weakness 

Muscle weakness
Other names	Myasthenia
Specialty	Neurology

Muscle weakness is a lack of muscle strength. Its causes are many and can be divided into conditions that have either true or perceived muscle weakness. True muscle weakness is a primary symptom of a variety of skeletal muscle diseases, including muscular dystrophy and inflammatory myopathy. It occurs in neuromuscular junction disorders, such as myasthenia gravis. Muscle weakness can also be caused by low levels of potassium and other electrolytes within muscle cells. It can be temporary or long-lasting (from seconds or minutes to months or years). The term myasthenia is from my- from Greek μυο meaning "muscle" + -asthenia ἀσθένεια meaning "weakness".

Types

Neuromuscular fatigue can be classified as either "central" or "peripheral" depending on its cause. Central muscle fatigue manifests as an overall sense of energy deprivation, while peripheral muscle fatigue manifests as a local, muscle-specific inability to do work.

Neuromuscular fatigue

Nerves control the contraction of muscles by determining the number, sequence, and force of muscular contraction. When a nerve experiences synaptic fatigue it becomes unable to stimulate the muscle that it innervates. Most movements require a force far below what a muscle could potentially generate, and barring pathology, neuromuscular fatigue is seldom an issue.

For extremely powerful contractions that are close to the upper limit of a muscle's ability to generate force, neuromuscular fatigue can become a limiting factor in untrained individuals. In novice strength trainers, the muscle's ability to generate force is most strongly limited by nerve’s ability to sustain a high-frequency signal. After an extended period of maximum contraction, the nerve’s signal reduces in frequency and the force generated by the contraction diminishes. There is no sensation of pain or discomfort, the muscle appears to simply ‘stop listening’ and gradually cease to move, often lengthening. As there is insufficient stress on the muscles and tendons, there will often be no delayed onset muscle soreness following the workout. Part of the process of strength training is increasing the nerve's ability to generate sustained, high frequency signals which allow a muscle to contract with their greatest force. It is this "neural training" that causes several weeks worth of rapid gains in strength, which level off once the nerve is generating maximum contractions and the muscle reaches its physiological limit. Past this point, training effects increase muscular strength through myofibrillar or sarcoplasmic hypertrophy and metabolic fatigue becomes the factor limiting contractile force.

Central fatigue

Central fatigue is a reduction in the neural drive or nerve-based motor command to working muscles that results in a decline in the force output. It has been suggested that the reduced neural drive during exercise may be a protective mechanism to prevent organ failure if the work was continued at the same intensity. There has been a great deal of interest in the role of serotonergic pathways for several years because its concentration in the brain increases with motor activity. During motor activity, serotonin released in synapses that contact motoneurons promotes muscle contraction. During high level of motor activity, the amount of serotonin released increases and a spillover occurs. Serotonin binds to extrasynaptic receptors located on the axon initial segment of motoneurons with the result that nerve impulse initiation and thereby muscle contraction are inhibited.

Peripheral muscle fatigue

Peripheral muscle fatigue during physical work is an inability for the body to supply sufficient energy or other metabolites to the contracting muscles to meet the increased energy demand. This is the most common case of physical fatigue—affecting a national average of 72% of adults in the work force in 2002. This causes contractile dysfunction that manifests in the eventual reduction or lack of ability of a single muscle or local group of muscles to do work. The insufficiency of energy, i.e. sub-optimal aerobic metabolism, generally results in the accumulation of lactic acid and other acidic anaerobic metabolic by-products in the muscle, causing the stereotypical burning sensation of local muscle fatigue, though recent studies have indicated otherwise, actually finding that lactic acid is a source of energy.

The fundamental difference between the peripheral and central theories of muscle fatigue is that the peripheral model of muscle fatigue assumes failure at one or more sites in the chain that initiates muscle contraction. Peripheral regulation therefore depends on the localized metabolic chemical conditions of the local muscle affected, whereas the central model of muscle fatigue is an integrated mechanism that works to preserve the integrity of the system by initiating muscle fatigue through muscle derecruitment, based on collective feedback from the periphery, before cellular or organ failure occurs. Therefore, the feedback that is read by this central regulator could include chemical and mechanical as well as cognitive cues. The significance of each of these factors will depend on the nature of the fatigue-inducing work that is being performed.

Though not universally used, "metabolic fatigue" is a common alternative term for peripheral muscle weakness, because of the reduction in contractile force due to the direct or indirect effects of the reduction of substrates or accumulation of metabolites within the muscle fiber. This can occur through a simple lack of energy to fuel contraction, or through interference with the ability of Ca²⁺ to stimulate actin and myosin to contract.

Lactic acid hypothesis

It was once believed that lactic acid build-up was the cause of muscle fatigue. The assumption was lactic acid had a "pickling" effect on muscles, inhibiting their ability to contract. The impact of lactic acid on performance is now uncertain, it may assist or hinder muscle fatigue.

Produced as a by-product of fermentation, lactic acid can increase intracellular acidity of muscles. This can lower the sensitivity of contractile apparatus to calcium ions (Ca²⁺) but also has the effect of increasing cytoplasmic Ca²⁺ concentration through an inhibition of the chemical pump that actively transports calcium out of the cell. This counters inhibiting effects of potassium ions (K⁺) on muscular action potentials. Lactic acid also has a negating effect on the chloride ions in the muscles, reducing their inhibition of contraction and leaving K⁺ as the only restricting influence on muscle contractions, though the effects of potassium are much less than if there were no lactic acid to remove the chloride ions. Ultimately, it is uncertain if lactic acid reduces fatigue through increased intracellular calcium or increases fatigue through reduced sensitivity of contractile proteins to Ca²⁺.

Pathophysiology

Main article: muscle contraction

Muscle cells work by detecting a flow of electrical impulses from the brain which signals them to contract through the release of calcium by the sarcoplasmic reticulum. Fatigue (reduced ability to generate force) may occur due to the nerve, or within the muscle cells themselves. New research from scientists at Columbia University suggests that muscle fatigue is caused by calcium leaking out of the muscle cell. This causes there to be less calcium available for the muscle cell. In addition an enzyme is proposed to be activated by this released calcium which eats away at muscle fibers.

Substrates within the muscle generally serve to power muscular contractions. They include molecules such as adenosine triphosphate (ATP), glycogen and creatine phosphate. ATP binds to the myosin head and causes the ‘ratchetting’ that results in contraction according to the sliding filament model. Creatine phosphate stores energy so ATP can be rapidly regenerated within the muscle cells from adenosine diphosphate (ADP) and inorganic phosphate ions, allowing for sustained powerful contractions that last between 5–7 seconds. Glycogen is the intramuscular storage form of glucose, used to generate energy quickly once intramuscular creatine stores are exhausted, producing lactic acid as a metabolic byproduct. Contrary to common belief, lactic acid accumulation doesn't actually cause the burning sensation we feel when we exhaust our oxygen and oxidative metabolism, but in actuality, lactic acid in presence of oxygen recycles to produce pyruvate in the liver which is known as the Cori cycle.

Substrates produce metabolic fatigue by being depleted during exercise, resulting in a lack of intracellular energy sources to fuel contractions. In essence, the muscle stops contracting because it lacks the energy to do so.

Diagnosis

Grading

The severity of muscle weakness can be classified into different "grades" based on the following criteria:

• Grade 0: No contraction or muscle movement.
• Grade 1: Trace of contraction, but no movement at the joint.
• Grade 2: Movement at the joint with gravity eliminated.
• Grade 3: Movement against gravity, but not against added resistance.
• Grade 4: Movement against external resistance with less strength than usual.
• Grade 5: Normal strength.

Classification

Proximal and distal

Muscle weakness can also be classified as either "proximal" or "distal" based on the location of the muscles that it affects. Proximal muscle weakness affects muscles closest to the body's midline, while distal muscle weakness affects muscles further out on the limbs. Proximal muscle weakness can be seen in Cushing's syndrome and hyperthyroidism.

True and perceived

Muscle weakness can be classified as either "true" or "perceived" based on its cause.

• True muscle weakness (or neuromuscular weakness) describes a condition where the force exerted by the muscles is less than would be expected, for example muscular dystrophy.
• Perceived muscle weakness (or non-neuromuscular weakness) describes a condition where a person feels more effort than normal is required to exert a given amount of force but actual muscle strength is normal, for example chronic fatigue syndrome.

In some conditions, such as myasthenia gravis, muscle strength is normal when resting, but true weakness occurs after the muscle has been subjected to exercise. This is also true for some cases of chronic fatigue syndrome, where objective post-exertion muscle weakness with delayed recovery time has been measured and is a feature of some of the published definitions.