Climate sensitivity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Climate_sensitivity 

 

Diagram of factors that determine climate sensitivity. After increasing CO
2 levels, there is an initial warming. This warming gets amplified by the net effect of feedbacks. Self-reinforcing feedbacks include the melting of sunlight-reflecting ice, and higher evaporation increasing average atmospheric water vapour (a greenhouse gas).

Climate sensitivity is a measure of how much the Earth's climate will cool or warm after a change in the climate system, for instance, how much it will warm for doubling in carbon dioxide (CO
2) concentrations. In technical terms, climate sensitivity is the average change in the Earth's surface temperature in response to changes in radiative forcing, the difference between incoming and outgoing energy on Earth. Climate sensitivity is a key measure in climate science, and a focus area for climate scientists, who want to understand the ultimate consequences of anthroprogenic climate change.

The Earth's surface warms as a direct consequence of increased atmospheric CO
2, as well as increased concentrations of other greenhouse gases such as nitrous oxide and methane. Increasing temperatures have secondary effects on the climate system, such as an increase in atmospheric water vapour, which is itself also a greenhouse gas. Because scientists do not know exactly how strong these climate feedbacks are, it is difficult to precisely predict the amount of warming that will result from a given increase in greenhouse gas concentrations. If climate sensitivity turns out to be on the high side of scientific estimates, the Paris Agreement goal of limiting global warming to below 2 °C (3.6 °F) will be difficult to achieve.

The two primary types of climate sensitivity are the shorter-term "transient climate response", the increase in global average temperature that is expected to have occurred at a time when the atmospheric CO
2 concentration has doubled; and "equilibrium climate sensitivity", the higher long-term increase in global average temperature expected to occur after the effects of a doubled CO
2 concentration have had time to reach a steady state. Climate sensitivity is typically estimated in three ways; using direct observations of temperature and levels of greenhouse gases taken during the industrial age; using indirectly estimated temperature and other measurements from the Earth's more distant past; and modelling the various aspects of the climate system with computers.

Background

The rate at which energy reaches Earth as sunlight, and leaves Earth as heat radiation to space, must balance, or the total amount of heat energy on the planet at any one time will rise or fall, resulting in a planet that is warmer or cooler overall. An imbalance between the rates of incoming and outgoing radiation energy is called radiative forcing. A warmer planet radiates heat to space faster, so eventually a new balance is reached, with a higher planetary temperature. However, the warming of the planet also has knock-on effects. These knock-on effects create further warming, in an exacerbating feedback loop. Climate sensitivity is a measure of how much temperature change a given amount of radiative forcing will cause.

Radiative forcing

Radiative forcing is generally defined as the imbalance between incoming and outgoing radiation at the top of the atmosphere. Radiative forcing is measured in Watts per square meter (W/m²), the average imbalance in energy per second for each square meter of the Earth's surface.

Changes to radiative forcing lead to long-term changes in global temperature. A number of factors can affect radiative forcing: increased downwelling radiation due to the greenhouse effect, variability in solar radiation due to changes in planetary orbit, changes in solar irradiance, direct and indirect effects caused by aerosols (for example changes in albedo due to cloud cover), and changes in land use (i.e. deforestation or loss of reflective ice cover). In contemporary research, radiative forcing by greenhouse gases is well understood. As of 2019, large uncertainties remain for aerosols.

Key numbers

Carbon dioxide (CO
2) levels rose from 280 parts per million (ppm) in the eighteenth century, when humans in the Industrial Revolution started burning significant amounts of fossil fuel such as coal, to over 415 ppm by 2020. As CO
2 is a greenhouse gas, it hinders heat energy from leaving the Earth's atmosphere. In 2016, atmospheric CO
2 levels had increased by 45% over preindustrial levels, and radiative forcing caused by increased CO
2 was already more than 50% higher than in preindustrial times (due to non-linear effects). Between the start of the Industrial Revolution in the eighteenth century and 2020, the Earth's temperature rose by a little over one degree Celsius (about two degrees Fahrenheit).

Societal importance

Because the economics of climate change mitigation depend a lot on how quickly carbon neutrality needs to be achieved, climate sensitivity estimates can have important economic and policy-making implications. One study suggests that halving the uncertainty of the value for transient climate response (TCR) could save trillions of dollars. Scientists are uncertain about the precision of estimates of greenhouse gas increases on future temperature – a higher climate sensitivity would mean more dramatic increases in temperature – which makes it more prudent to take significant climate action. If climate sensitivity turns out to be on the high end of what scientists estimate, it will be impossible to achieve the Paris Agreement goal of limiting global warming to well below 2 °C; temperature increases will exceed that limit, at least temporarily. One study estimated that emissions cannot be reduced fast enough to meet the 2 °C goal if equilibrium climate sensitivity (the long-term measure) is higher than 3.4 °C (6.1 °F). The more sensitive the climate system is to changes in greenhouse gas concentrations, the more likely it is to have decades when temperatures are much higher or much lower than the longer-term average.

Contributors to climate sensitivity

Radiative forcing is one component of climate sensitivity. The radiative forcing caused by a doubling of atmospheric CO
2 levels (from the preindustrial 280 ppm) is approximately 3.7 watts per square meter (W/m²). In the absence of feedbacks, this energy imbalance would eventually result in roughly 1 °C (1.8 °F) of global warming. This figure is straightforward to calculate using the Stefan-Boltzmann law and is undisputed.

A further contribution arises from climate feedbacks, both exacerbating and suppressing. The uncertainty in climate sensitivity estimates is due entirely to modeling of feedbacks in the climate system, including water vapour feedback, ice-albedo feedback, cloud feedback, and lapse rate feedback. Suppressing feedbacks tend to counteract warming, increasing the rate at which energy is radiated to space from a warmer planet. Exacerbating feedbacks increase warming; for example, higher temperatures can cause ice to melt, reducing the ice area and the amount of sunlight the ice reflects, resulting in less heat energy being radiated back into space. Climate sensitivity depends on the balance between these feedbacks.

Measures of climate sensitivity

Schematic of how different measures of climate sensitivity relate to one another

Depending on the time scale, there are two main ways to define climate sensitivity: the short-term transient climate response (TCR) and the long-term equilibrium climate sensitivity (ECS), which both incorporate the warming from exacerbating feedback loops. These are not discrete categories; they overlap. Sensitivity to atmospheric CO
2 increases is measured in the amount of temperature change for doubling in the atmospheric CO
2 concentration.

Although "climate sensitivity" is usually used for the sensitivity to radiative forcing caused by rising atmospheric CO
2, it is a general property of the climate system. Other agents can also cause a radiative imbalance. Climate sensitivity is the change in surface air temperature per unit change in radiative forcing, and the climate sensitivity parameter is therefore expressed in units of °C/(W/m²). Climate sensitivity is approximately the same, whatever the reason for the radiative forcing (e.g. from greenhouse gases or solar variation). When climate sensitivity is expressed as the temperature change for a level of atmospheric CO
2 double the pre-industrial level, its units are degrees Celsius (°C).

Transient climate response

The transient climate response (TCR) is defined as "is the change in the global mean surface temperature, averaged over a 20-year period, centered at the time of atmospheric carbon dioxide doubling, in a climate model simulation" in which the atmospheric CO
2 concentration is increasing at 1% per year. This estimate is generated using shorter-term simulations. The transient response is lower than the equilibrium climate sensitivity, because slower feedbacks, which exacerbate the temperature increase, take more time to respond in full to an increase in the atmospheric CO
2 concentration. For instance, the deep ocean takes many centuries to reach a new steady state after a perturbation; during this time, it continues to serve as heatsink, cooling the upper ocean. The IPCC literature assessment estimates that TCR likely lies between 1 °C (1.8 °F) and 2.5 °C (4.5 °F).

A related measure is the transient climate response to cumulative carbon emissions (TCRE), which is the globally averaged surface temperature change after 1000 GtC of CO
2 has been emitted. As such, it includes not only temperature feedbacks to forcing, but also the carbon cycle and carbon cycle feedbacks.

Equilibrium climate sensitivity

The equilibrium climate sensitivity (ECS) is the long-term temperature rise (equilibrium global mean near-surface air temperature) that is expected to result from a doubling of the atmospheric CO
2 concentration (ΔT_2×). It is a prediction of the new global mean near-surface air temperature once the CO
2 concentration has stopped increasing and most of the feedbacks have had time to have their full effect. Reaching an equilibrium temperature can take centuries, or even millennia, after CO
2 has doubled. ECS is higher than TCR due to the oceans' short-term buffering effects. Computer models are used to estimate ECS. A comprehensive estimate means modelling the whole time span during which significant feedbacks continue to change global temperatures in the model; for instance, fully equilibrating ocean temperatures requires running a computer model that covers thousands of years. There are, however, less computing-intensive methods.

The IPCC Fifth Assessment Report (AR5) stated that "there is high confidence that ECS is extremely unlikely to be less than 1 °C and medium confidence that the ECS is likely between 1.5 °C and 4.5 °C and very unlikely greater than 6 °C". The long time scales involved with ECS make it arguably a less relevant measure for policy decisions around climate change.

Effective climate sensitivity

A common approximation to ECS is the effective equilibrium climate sensitivity. The effective climate sensitivity is an estimate of equilibrium climate sensitivity using data from a climate system, either in a model or real-world observations, that is not yet in equilibrium. Estimates assume that the net amplification effect of feedbacks (as measured after some period of warming) will remain constant afterwards. This is not necessarily true, as feedbacks can change with time. In many climate models, feedbacks become stronger over time, so that the effective climate sensitivity is lower than the real ECS.

Earth system sensitivity

By definition, equilibrium climate sensitivity does not includes feedbacks that take millennia to emerge, such as long-term changes in Earth's albedo due to changes in ice sheets and vegetation. It does include the slow response of the deep ocean warming up, which also takes millennia, and as such ECS doesn't reflect the actual future warming that would occur if CO
2 is stabilized at double pre-industrial values. Earth system sensitivity (ESS) incorporates the effects of these slower feedback loops, such as the change in Earth's albedo from the melting of large continental ice sheets (which covered much of the northern hemisphere during the Last Glacial Maximum, and currently cover Greenland and Antarctica). Changes in albedo as a result of vegetation changes, and changes in ocean circulations are also included. These longer-term feedback loops make the ESS larger than the ECS – possibly twice as large. Data from Earth's geological history is used to estimate ESS. Differences between modern and long-past climatic conditions mean that estimates of future ESS are highly uncertain. Like for ECS and TCR, the carbon cycle is not included in the definition of ESS, but all other elements of the climate system are.

Sensitivity to nature of the forcing

Different forcing agents, such as greenhouse gases and aerosols, can be compared using their radiative forcing (which is the initial radiative imbalance averaged over the entire globe). Climate sensitivity is the amount of warming per radiative forcing. To a first approximation, it does not matter the cause of the radiative imbalance is, whether it is greenhouse gases or something else. However, radiative forcing from sources other than CO
2 can cause a somewhat larger or smaller surface warming than a similar radiative forcing due to CO
2; the amount of feedback varies, mainly because these forcings are not uniformly distributed over the globe. Forcings that initially warm the northern hemisphere, land, or polar regions more strongly are systematically more effective at changing temperatures than an equivalent forcing due to CO
2, whose forcing is more uniformly distributed over the globe. This is because these regions have more self-reinforcing feedbacks, such as the ice-albedo feedback. Several studies indicate that human-emitted aerosols are more effective than CO
2 at changing global temperatures, while volcanic forcing is less effective. When climate sensitivity to CO
2 forcing is estimated using historical temperature and forcing (caused by a mix of aerosols and greenhouse gases), and this effect is not taken into account, climate sensitivity will be underestimated.

State dependence

Artist impression of a snowball Earth state.

While climate sensitivity has been defined as the short- or long-term temperature change resulting from any doubling of CO
2, there is evidence that the sensitivity of Earth's climate system is not constant. For instance, the planet has polar ice and high-altitude glaciers. Until the world's ice has completely melted, an exacerbating ice-albedo feedback loop makes the system more sensitive overall. Throughout Earth's history, there are thought to have been multiple periods where snow and ice covered almost the entire globe. In most models of this "snowball Earth" state, parts of the tropics were at least intermittently free of ice cover. As the ice was advancing or retreating, climate sensitivity would have been very high, as the large changes in area of ice cover would have made for a very strong ice-albedo feedback. Volcanic atmospheric composition changes are thought to have provided the radiative forcing needed to escape the snowball state.

Equilibrium climate sensitivity can change with climate.

Throughout the Quaternary period (the most recent 2.58 million years), climate has oscillated between glacial periods, of which the most recent was the Last Glacial Maximum, and interglacial periods, of which the most recent is the current Holocene, but climate sensitivity is difficult to determine in this period. The Paleocene–Eocene Thermal Maximum, circa 55.5 million years ago, was unusually warm, and may have been characterized by above-average climate sensitivity.

Climate sensitivity may further change if tipping points are crossed. It is unlikely that tipping points will cause short-term changes in climate sensitivity. If a tipping point is crossed, climate sensitivity is expected to change at the time scale of the subsystem that is hitting its tipping point. Especially if there are multiple interacting tipping points, the transition of climate to a new state may be difficult to reverse.

The two most used definitions of climate sensitivity specify the climate state: ECS and TCR are defined for a doubling with respect to the CO
2 levels in the pre-industrial era. Because of potential changes in climate sensitivity, the climate system may warm by a different amount after a second doubling of CO
2 than after a first doubling. The effect of any change in climate sensitivity is expected to be small or negligible in the first century after additional CO
2 is released into the atmosphere.

Estimating climate sensitivity

Historical estimates

Svante Arrhenius, in the 19th century, was the first person to quantify global warming as a consequence of a doubling of CO
2 concentration. In his first paper on the matter, he estimated that global temperature would rise by around 5 to 6 °C (9.0 to 10.8 °F) if the quantity of CO
2 was doubled. In later work, he revised this estimate to 4 °C (7.2 °F). Arrhenius used Samuel Pierpont Langley's observations of radiation emitted by the full moon to estimate the amount of radiation that was absorbed by water vapour and CO
2. To account for water vapour feedback, he assumed that relative humidity would stay the same under global warming.

The first calculation of climate sensitivity using detailed measurements of absorption spectra, and the first to use a computer to numerically integrate the radiative transfer through the atmosphere, was performed by Syukuro Manabe and Richard Wetherald in 1967. Assuming constant humidity, they computed an equilibrium climate sensitivity of 2.3 °C per doubling of CO
2 (which they rounded to 2 °C, the value most often quoted from their work, in the abstract of the paper). This work has been called "arguably the greatest climate-science paper of all time" and "the most influential study of climate of all time."

A committee on anthropogenic global warming, convened in 1979 by the United States National Academy of Sciences and chaired by Jule Charney, estimated equilibrium climate sensitivity to be 3 °C (5.4 °F), plus or minus 1.5 °C (2.7 °F). The Manabe and Wetherald estimate (2 °C (3.6 °F)), James E. Hansen's estimate of 4 °C (7.2 °F), and Charney's model were the only models available in 1979. According to Manabe, speaking in 2004, "Charney chose 0.5 °C as a reasonable margin of error, subtracted it from Manabe's number, and added it to Hansen's, giving rise to the 1.5 to 4.5 °C (2.7 to 8.1 °F) range of likely climate sensitivity that has appeared in every greenhouse assessment since ...." In 2008, climatologist Stefan Rahmstorf said: "At that time [it was published], the [Charney report estimate's] range [of uncertainty] was on very shaky ground. Since then, many vastly improved models have been developed by a number of climate research centers around the world."

Intergovernmental Panel on Climate Change

Historical estimates of climate sensitivity from the IPCC assessments. The first three reports gave a qualitative likely range, while the fourth and fifth assessment report formally quantified the uncertainty. The dark blue range is judged as being more than 66% likely.

Despite considerable progress in the understanding of Earth's climate system, assessments continued to report similar uncertainty ranges for climate sensitivity for some time after the 1979 Charney report. The 1990 IPCC First Assessment Report estimated that equilibrium climate sensitivity to a doubling of CO
2 lay between 1.5 and 4.5 °C (2.7 and 8.1 °F), with a "best guess in the light of current knowledge" of 2.5 °C (4.5 °F). This report used models with simplified representations of ocean dynamics. The IPCC supplementary report, 1992, which used full-ocean circulation models, saw "no compelling reason to warrant changing" the 1990 estimate; and the IPCC Second Assessment Report said that "No strong reasons have emerged to change [these estimates]". In these reports, much of the uncertainty around climate sensitivity was attributed to insufficient knowledge of cloud processes. The 2001 IPCC Third Assessment Report also retained this likely range.

Authors of the 2007 IPCC Fourth Assessment Report stated that confidence in estimates of equilibrium climate sensitivity had increased substantially since the Third Annual Report. The IPCC authors concluded that ECS is very likely to be greater than 1.5 °C (2.7 °F) and likely to lie in the range 2 to 4.5 °C (3.6 to 8.1 °F), with a most likely value of about 3 °C (5.4 °F). The IPCC stated that, due to fundamental physical reasons and data limitations, a climate sensitivity higher than 4.5 °C (8.1 °F) could not be ruled out, but that the climate sensitivity estimates in the likely range agreed better with observations and proxy climate data.

The 2013 IPCC Fifth Assessment Report reverted to the earlier range of 1.5 to 4.5 °C (2.7 to 8.1 °F) (with high confidence), because some estimates using industrial-age data came out low. (See the next section for details.) The report also stated that ECS is extremely unlikely to be less than 1 °C (1.8 °F) (high confidence), and is very unlikely to be greater than 6 °C (11 °F) (medium confidence). These values were estimated by combining the available data with expert judgement.

When the Ipcc begun to produce its IPCC Sixth Assessment Report many climate models begun to show higher climate sensitivity. The estimates for Equilibrium Climate Sensitivity changed from 3.2 °C to 3.7 °C and the estimates for the Transient climate response from 1.8 °C, to 2.0 °C. This is probably due to better understanding of the role of clouds and aerosols.

Methods of estimation

Using industrial-age (1750–present) data

Climate sensitivity can be estimated using observed temperature rise, observed ocean heat uptake, and modelled or observed radiative forcing. These data are linked though a simple energy-balance model to calculate climate sensitivity. Radiative forcing is often modelled, because Earth observation satellites that measure it existed during only part of the industrial age (only since the mid-20th century). Estimates of climate sensitivity calculated using these global energy constraints have consistently been lower than those calculated using other methods, around 2 °C (3.6 °F) or lower.

Estimates of transient climate response (TCR) calculated from models and observational data can be reconciled if it is taken into account that fewer temperature measurements are taken in the polar regions, which warm more quickly than the Earth as a whole. If only regions for which measurements are available are used in evaluating the model, differences in TCR estimates are negligible.

A very simple climate model could estimate climate sensitivity from industrial-age data by waiting for the climate system to reach equilibrium and then measuring the resulting warming, ΔT_eq (°C). Computation of the equilibrium climate sensitivity, S (°C), using the radiative forcing ΔF (W/m²) and the measured temperature rise, would then be possible. The radiative forcing resulting from a doubling of CO
2, F_{2${\displaystyle \times }$CO2}, is relatively well known, at about 3.7 W/m². Combining this information results in the following equation:

${\displaystyle S=\Delta T_{eq}\times F_{2\times CO_{2}}/\Delta F}$.

However, the climate system is not in equilibrium. Actual warming lags the equilibrium warming, largely because the oceans take up heat and will take centuries or millennia to reach equilibrium. Estimating climate sensitivity from industrial-age data requires an adjustment to the equation above. The actual forcing felt by the atmosphere is the radiative forcing minus the ocean's heat uptake, H (W/m²), so that climate sensitivity can be estimated by:

${\displaystyle S=\Delta T\times F_{2\times CO_{2}}/(\Delta F-H).}$

The global temperature increase between the beginning of the industrial period (taken as 1750) and 2011 was about 0.85 °C (1.53 °F). In 2011, the radiative forcing due to CO
2 and other long-lived greenhouse gases – mainly methane, nitrous oxide, and chlorofluorocarbons – emitted since the eighteenth century was roughly 2.8 W/m². The climate forcing, ΔF, also contains contributions from solar activity (+0.05 W/m²), aerosols (−0.9 W/m²), ozone (+0.35 W/m²), and other smaller influences, bringing the total forcing over the industrial period to 2.2 W/m², according to the best estimate of the IPCC AR5, with substantial uncertainty. The ocean heat uptake estimated by the IPCC AR5 as 0.42 W/m², yields a value for S of 1.8 °C (3.2 °F).

Other strategies

In theory, industrial-age temperatures could also be used to determine a timescale for the temperature response of the climate system, and thus climate sensitivity: if the effective heat capacity of the climate system is known, and the timescale is estimated using autocorrelation of the measured temperature, an estimate of climate sensitivity can be derived. In practice, however, simultaneous determination of the timescale and heat capacity is difficult.

Attempts have been made to use the 11-year solar cycle to constrain the transient climate response. Solar irradiance is about 0.9 W/m² higher during a solar maximum than during a solar minimum, and the effects of this can be observed in measured average global temperatures over the period 1959–2004. Unfortunately, the solar minima in this period coincided with volcanic eruptions, which have a cooling effect on the global temperature. Because the eruptions caused a larger and less well quantified decrease in radiative forcing than the reduced solar irradiance, it is questionable whether useful quantitative conclusions can be derived from the observed temperature variations.

Observations of volcanic eruptions have also been used to try to estimate climate sensitivity, but as the aerosols from a single eruption last at most a couple of years in the atmosphere, the climate system can never come close to equilibrium, and there is less cooling than there would be if the aerosols stayed in the atmosphere for longer. Therefore, volcanic eruptions give information only about a lower bound on transient climate sensitivity.

Using data from Earth's past

Historical climate sensitivity can be estimated by using reconstructions of Earth's past temperatures and CO
2 levels. Paleoclimatologists have studied different geological periods, such as the warm Pliocene (5.3 to 2.6 million years ago) and the colder Pleistocene (2.6 million to 11,700 years ago), seeking periods that are in some way analogous to or informative about current climate change. Climates further back in Earth's history are more difficult to study, because less data is available about them. For instance, past CO
2 concentrations can be derived from air trapped in ice cores, but as of 2020, the oldest continuous ice core is less than one million years old. Recent periods, such as the Last Glacial Maximum (LGM) (about 21,000 years ago) and the Mid-holocene (about 6,000 years ago), are often studied, especially when more information about them becomes available.

A 2007 estimate of sensitivity made using data from the most recent 420 million years is consistent with sensitivities of current climate models and with other determinations. The Paleocene–Eocene Thermal Maximum (about 55.5 million years ago), a 20,000-year period during which massive amount of carbon entered the atmosphere and average global temperatures increased by approximately 6 °C (11 °F), also provides a good opportunity to study the climate system when it was in a warm state. Studies of the last 800,000 years have concluded that climate sensitivity was greater in glacial periods than in interglacial periods.

As the name suggests, the LGM was a lot colder than today; there is good data on atmospheric CO
2 concentrations and radiative forcing during that period. While orbital forcing was different from that of the present, it had little effect on mean annual temperatures. Estimating climate sensitivity from the LGM can be done in several different ways. One way is to use estimates of global radiative forcing and temperature directly. The set of feedback mechanisms active during the LGM, however, may be different from the feedbacks caused by a doubling of CO
2 in the present, introducing additional uncertainty. In a different approach, a model of intermediate complexity is used to simulate conditions during the LGM. Several versions of this single model are run, with different values chosen for uncertain parameters, such that each version has a different ECS. Outcomes that best simulate observed cooling during the LGM probably produce the most realistic ECS values.

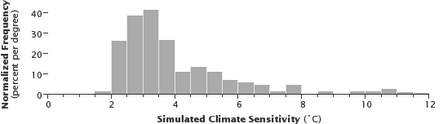
Using climate models

Frequency distribution of equilibrium climate sensitivity, based on simulations of doubling CO
2. Each model simulation has different estimates for processes that scientists do not sufficiently understand. Few of the simulations result in less than 2 °C (3.6 °F) of warming or significantly more than 4 °C (7.2 °F). However, the positive skew, which is also found in other studies, suggests that if carbon dioxide concentrations double, the probability of large or very large increases in temperature is greater than the probability of small increases.

Climate models are used to simulate the CO
2-driven warming of the future as well as the past. They operate on principles similar to those underlying models that predict the weather, but they focus on longer-term processes. Climate models typically begin with a starting state, then apply physical laws and knowledge about biology to generate subsequent states. As with weather modeling, no computer has the power to model the full complexity of the entire planet, so simplifications are used to reduce this complexity to something manageable. An important simplification divides Earth's atmosphere into model cells. For instance, the atmosphere might be divided into cubes of air ten or one hundred kilometers on a side. Each model cell is treated as if it were homogeneous. Calculations for model cells are much faster than trying to simulate each molecule of air separately.

A lower model resolution (large model cells, long time steps) takes less computing power, but it cannot simulate the atmosphere in as much detail. A model is unable able to simulate processes smaller than the model cells or shorter-term than a single time step. The effects of these smaller-scale (and shorter-term) processes must therefore be estimated using other methods. Physical laws contained in the models may also be simplified to speed up calculations. The biosphere must be included in climate models. The effects of the biosphere are estimated using data on the average behaviour of the average plant assemblage of an area under the modelled conditions. Climate sensitivity is therefore an emergent property of these models; it is not prescribed, but follows from the interaction of all the modelled processes.

To estimate climate sensitivity, a model is run using a variety of radiative forcings (doubling quickly, doubling gradually, or following historical emissions) and the temperature results are compared to the forcing applied. Different models give different estimates of climate sensitivity, but they tend to fall within a similar range, as described above.

Testing, comparisons, and estimates

Modelling of the climate system can lead to a wide range of outcomes. Models are often run using different plausible parameters in their approximation of physical laws and the behaviour of the biosphere, forming a perturbed physics ensemble that attempts to model the sensitivity of the climate to different types and amounts of change in each parameter. Alternatively, structurally different models developed at different institutions are put together, creating an ensemble. By selecting only those simulations that can simulate some part of the historical climate well, a constrained estimate of climate sensitivity can be made. One strategy for obtaining more accurate results is placing more emphasis on climate models that perform well in general.

A model is tested using observations, paleoclimate data, or both to see if it replicates them accurately. If it does not, inaccuracies in the physical model and parametrizations are sought and the model is modified. For models used to estimate climate sensitivity, specific test metrics that are directly and physically linked to climate sensitivity are sought; examples of such metrics are the global patterns of warming, the ability of a model to reproduce observed relative humidity in the tropics and subtropics, patterns of heat radiation, and the variability of temperature around long-term historical warming. Ensemble climate models developed at different institutions tend to produce constrained estimates of ECS that are slightly higher than 3 °C (5.4 °F); the models with ECS slightly above 3 °C (5.4 °F) simulate the above situations better than models with a lower climate sensitivity.

Many projects and groups exist which compare and analyse the results of multiple models. For instance, the Coupled Model Intercomparison Project (CMIP) has been running since the 1990s.

In preparation for the 2021 6th IPCC report, a new generation of climate models have been developed by scientific groups around the world. The average estimated climate sensitivity has increased in Coupled Model Intercomparison Project phase 6 (CMIP6) compared to the previous generation, with values spanning 1.8 to 5.6 °C (3.2 to 10.1 °F) across 27 global climate models and exceeding 4.5 °C (8.1 °F) in 10 of them. The cause of the increased ECS lies mainly in improved modelling of clouds; temperature rises are now believed to cause sharper decreases in the number of low clouds, and fewer low clouds means more sunlight is absorbed by the planet rather than reflected back into space. Models with the highest ECS values, however, are not consistent with observed warming.