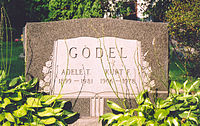Kurt Friedrich Gödel (/ˈɡɜːrdəl/; German: [ˈkʊɐ̯t ˈɡøːdl̩]; April 28, 1906 – January 14, 1978) was a logician, mathematician, and philosopher. Considered along with Aristotle and Gottlob Frege to be one of the most significant logicians in history, Gödel had an immense effect upon scientific and philosophical thinking in the 20th century, a time when others such as Bertrand Russell, Alfred North Whitehead, and David Hilbert were using logic and set theory to investigate the foundations of mathematics, building on earlier work by the likes of Richard Dedekind, Georg Cantor and Gottlob Frege.
Gödel published his first incompleteness theorem in 1931 when he was 25 years old, one year after finishing his doctorate at the University of Vienna. The first incompleteness theorem states that for any ω-consistent recursive axiomatic system powerful enough to describe the arithmetic of the natural numbers (for example Peano arithmetic), there are true propositions about the natural numbers that can be neither proved nor disproved from the axioms. To prove this, Gödel developed a technique now known as Gödel numbering, which codes formal expressions as natural numbers. The second incompleteness theorem, which follows from the first, states that the system cannot prove its own consistency.
Gödel also showed that neither the axiom of choice nor the continuum hypothesis can be disproved from the accepted Zermelo-Fraenkel set theory, assuming that its axioms are consistent. The former result opened the door for mathematicians to assume the axiom of choice in their proofs. He also made important contributions to proof theory by clarifying the connections between classical logic, intuitionistic logic, and modal logic.
Early life and education
Childhood
Gödel was born April 28, 1906, in Brünn, Austria-Hungary (now Brno, Czech Republic) into the German-speaking family of Rudolf Gödel (1874–1929), the manager of a textile factory, and Marianne Gödel (née Handschuh, 1879–1966). Throughout his life, Gödel would remain close to his mother; their correspondence was frequent and wide-ranging. At the time of his birth the city had a German-speaking majority which included his parents. His father was Catholic and his mother was Protestant and the children were raised Protestant. The ancestors of Kurt Gödel were often active in Brünn's cultural life. For example, his grandfather Joseph Gödel was a famous singer in his time and for some years a member of the Brünner Männergesangverein (Men's Choral Union of Brünn).
Gödel automatically became a citizen of Czechoslovakia at age 12 when the Austro-Hungarian Empire collapsed following its defeat in the First World War. (According to his classmate Klepetař, like many residents of the predominantly German Sudetenländer, "Gödel considered himself always Austrian and an exile in Czechoslovakia".) In February 1929, he was granted release from his Czechoslovakian citizenship and then, in April, granted Austrian citizenship. When Germany annexed Austria in 1938, Gödel automatically became a German citizen at age 32. In 1948, after World War II, at the age of 42, he became an American citizen.
In his family, the young Gödel was nicknamed Herr Warum ("Mr. Why") because of his insatiable curiosity. According to his brother Rudolf, at the age of six or seven, Kurt suffered from rheumatic fever; he completely recovered, but for the rest of his life he remained convinced that his heart had suffered permanent damage. Beginning at age four, Gödel suffered from "frequent episodes of poor health", which would continue for his entire life.
Gödel attended the Evangelische Volksschule, a Lutheran school in Brünn from 1912 to 1916, and was enrolled in the Deutsches Staats-Realgymnasium from 1916 to 1924, excelling with honors in all his subjects, particularly in mathematics, languages and religion. Although Gödel had first excelled in languages, he later became more interested in history and mathematics. His interest in mathematics increased when in 1920 his older brother Rudolf (born 1902) left for Vienna, where he attended medical school at the University of Vienna. During his teens, Gödel studied Gabelsberger shorthand, Goethe's Theory of Colours and criticisms of Isaac Newton, and the writings of Immanuel Kant.
Studies in Vienna
At the age of 18, Gödel joined his brother at the University of Vienna. By that time, he had already mastered university-level mathematics. Although initially intending to study theoretical physics, he also attended courses on mathematics and philosophy. During this time, he adopted ideas of mathematical realism. He read Kant's Metaphysische Anfangsgründe der Naturwissenschaft, and participated in the Vienna Circle with Moritz Schlick, Hans Hahn, and Rudolf Carnap. Gödel then studied number theory, but when he took part in a seminar run by Moritz Schlick which studied Bertrand Russell's book Introduction to Mathematical Philosophy, he became interested in mathematical logic. According to Gödel, mathematical logic was "a science prior to all others, which contains the ideas and principles underlying all sciences."
Attending a lecture by David Hilbert in Bologna on completeness and consistency in mathematical systems may have set Gödel's life course. In 1928, Hilbert and Wilhelm Ackermann published Grundzüge der theoretischen Logik (Principles of Mathematical Logic), an introduction to first-order logic in which the problem of completeness was posed: "Are the axioms of a formal system sufficient to derive every statement that is true in all models of the system?"
This problem became the topic that Gödel chose for his doctoral work. In 1929, at the age of 23, he completed his doctoral dissertation under Hans Hahn's supervision. In it, he established his eponymous completeness theorem regarding the first-order predicate calculus. He was awarded his doctorate in 1930, and his thesis (accompanied by some additional work) was published by the Vienna Academy of Science.
Career
Incompleteness theorem
Kurt Gödel's achievement in modern logic is singular and monumental—indeed it is more than a monument, it is a landmark which will remain visible far in space and time. ... The subject of logic has certainly completely changed its nature and possibilities with Gödel's achievement.
In 1930 Gödel attended the Second Conference on the Epistemology of the Exact Sciences, held in Königsberg, 5–7 September. Here he delivered his incompleteness theorems.
Gödel published his incompleteness theorems in Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (called in English "On Formally Undecidable Propositions of Principia Mathematica and Related Systems"). In that article, he proved for any computable axiomatic system that is powerful enough to describe the arithmetic of the natural numbers (e.g., the Peano axioms or Zermelo–Fraenkel set theory with the axiom of choice), that:
- If a (logical or axiomatic formal) system is omega-consistent, it cannot be syntactically complete.
- The consistency of axioms cannot be proved within their own system.
These theorems ended a half-century of attempts, beginning with the work of Frege and culminating in Principia Mathematica and Hilbert's formalism, to find a set of axioms sufficient for all mathematics.
In hindsight, the basic idea at the heart of the incompleteness theorem is rather simple. Gödel essentially constructed a formula that claims that it is unprovable in a given formal system. If it were provable, it would be false. Thus there will always be at least one true but unprovable statement. That is, for any computably enumerable set of axioms for arithmetic (that is, a set that can in principle be printed out by an idealized computer with unlimited resources), there is a formula that is true of arithmetic, but which is not provable in that system. To make this precise, however, Gödel needed to produce a method to encode (as natural numbers) statements, proofs, and the concept of provability; he did this using a process known as Gödel numbering.
In his two-page paper Zum intuitionistischen Aussagenkalkül (1932) Gödel refuted the finite-valuedness of intuitionistic logic. In the proof, he implicitly used what has later become known as Gödel–Dummett intermediate logic (or Gödel fuzzy logic).
Mid-1930s: further work and U.S. visits
Gödel earned his habilitation at Vienna in 1932, and in 1933 he became a Privatdozent (unpaid lecturer) there. In 1933 Adolf Hitler came to power in Germany, and over the following years the Nazis rose in influence in Austria, and among Vienna's mathematicians. In June 1936, Moritz Schlick, whose seminar had aroused Gödel's interest in logic, was assassinated by one of his former students, Johann Nelböck. This triggered "a severe nervous crisis" in Gödel. He developed paranoid symptoms, including a fear of being poisoned, and spent several months in a sanitarium for nervous diseases.
In 1933, Gödel first traveled to the U.S., where he met Albert Einstein, who became a good friend. He delivered an address to the annual meeting of the American Mathematical Society. During this year, Gödel also developed the ideas of computability and recursive functions to the point where he was able to present a lecture on general recursive functions and the concept of truth. This work was developed in number theory, using Gödel numbering.
In 1934, Gödel gave a series of lectures at the Institute for Advanced Study (IAS) in Princeton, New Jersey, entitled On undecidable propositions of formal mathematical systems. Stephen Kleene, who had just completed his PhD at Princeton, took notes of these lectures that have been subsequently published.
Gödel visited the IAS again in the autumn of 1935. The travelling and the hard work had exhausted him and the next year he took a break to recover from a depressive episode. He returned to teaching in 1937. During this time, he worked on the proof of consistency of the axiom of choice and of the continuum hypothesis; he went on to show that these hypotheses cannot be disproved from the common system of axioms of set theory.
He married Adele Nimbursky (née Porkert, 1899–1981), whom he had known for over 10 years, on September 20, 1938. Gödel's parents had opposed their relationship because she was a divorced dancer, six years older than he was.
Subsequently, he left for another visit to the United States, spending the autumn of 1938 at the IAS and publishing Consistency of the axiom of choice and of the generalized continuum-hypothesis with the axioms of set theory, a classic of modern mathematics. In that work he introduced the constructible universe, a model of set theory in which the only sets that exist are those that can be constructed from simpler sets. Gödel showed that both the axiom of choice (AC) and the generalized continuum hypothesis (GCH) are true in the constructible universe, and therefore must be consistent with the Zermelo–Fraenkel axioms for set theory (ZF). This result has had considerable consequences for working mathematicians, as it means they can assume the axiom of choice when proving the Hahn–Banach theorem. Paul Cohen later constructed a model of ZF in which AC and GCH are false; together these proofs mean that AC and GCH are independent of the ZF axioms for set theory.
Gödel spent the spring of 1939 at the University of Notre Dame.
Princeton, Einstein, U.S. citizenship
After the Anschluss on 12 March 1938, Austria had become a part of Nazi Germany. Germany abolished the title Privatdozent, so Gödel had to apply for a different position under the new order. His former association with Jewish members of the Vienna Circle, especially with Hahn, weighed against him. The University of Vienna turned his application down.
His predicament intensified when the German army found him fit for conscription. World War II started in September 1939. Before the year was up, Gödel and his wife left Vienna for Princeton. To avoid the difficulty of an Atlantic crossing, the Gödels took the Trans-Siberian Railway to the Pacific, sailed from Japan to San Francisco (which they reached on March 4, 1940), then crossed the US by train to Princeton. There Gödel accepted a position at the Institute for Advanced Study (IAS), which he had previously visited during 1933–34.
Albert Einstein was also living at Princeton during this time. Gödel and Einstein developed a strong friendship, and were known to take long walks together to and from the Institute for Advanced Study. The nature of their conversations was a mystery to the other Institute members. Economist Oskar Morgenstern recounts that toward the end of his life Einstein confided that his "own work no longer meant much, that he came to the Institute merely ... to have the privilege of walking home with Gödel".
Gödel and his wife, Adele, spent the summer of 1942 in Blue Hill, Maine, at the Blue Hill Inn at the top of the bay. Gödel was not merely vacationing but had a very productive summer of work. Using Heft 15 [volume 15] of Gödel's still-unpublished Arbeitshefte [working notebooks], John W. Dawson Jr. conjectures that Gödel discovered a proof for the independence of the axiom of choice from finite type theory, a weakened form of set theory, while in Blue Hill in 1942. Gödel's close friend Hao Wang supports this conjecture, noting that Gödel's Blue Hill notebooks contain his most extensive treatment of the problem.
On December 5, 1947, Einstein and Morgenstern accompanied Gödel to his U.S. citizenship exam, where they acted as witnesses. Gödel had confided in them that he had discovered an inconsistency in the U.S. Constitution that could allow the U.S. to become a dictatorship; this has since been dubbed Gödel's Loophole. Einstein and Morgenstern were concerned that their friend's unpredictable behavior might jeopardize his application. The judge turned out to be Phillip Forman, who knew Einstein and had administered the oath at Einstein's own citizenship hearing. Everything went smoothly until Forman happened to ask Gödel if he thought a dictatorship like the Nazi regime could happen in the U.S. Gödel then started to explain his discovery to Forman. Forman understood what was going on, cut Gödel off, and moved the hearing on to other questions and a routine conclusion.
Gödel became a permanent member of the Institute for Advanced Study at Princeton in 1946. Around this time he stopped publishing, though he continued to work. He became a full professor at the Institute in 1953 and an emeritus professor in 1976.
During his time at the Institute, Gödel's interests turned to philosophy and physics. In 1949, he demonstrated the existence of solutions involving closed timelike curves, to Einstein's field equations in general relativity. He is said to have given this elaboration to Einstein as a present for his 70th birthday. His "rotating universes" would allow time travel to the past and caused Einstein to have doubts about his own theory. His solutions are known as the Gödel metric (an exact solution of the Einstein field equation).
He studied and admired the works of Gottfried Leibniz, but came to believe that a hostile conspiracy had caused some of Leibniz's works to be suppressed. To a lesser extent he studied Immanuel Kant and Edmund Husserl. In the early 1970s, Gödel circulated among his friends an elaboration of Leibniz's version of Anselm of Canterbury's ontological proof of God's existence. This is now known as Gödel's ontological proof.
Awards and honours
Gödel was awarded (with Julian Schwinger) the first Albert Einstein Award in 1951, and was also awarded the National Medal of Science, in 1974. Gödel was elected a resident member of the American Philosophical Society in 1961 and a Foreign Member of the Royal Society (ForMemRS) in 1968. He was a Plenary Speaker of the ICM in 1950 in Cambridge, Massachusetts. The Gödel Prize, an annual prize for outstanding papers in the area of theoretical computer science, is named after him.
Later life and death
Later in his life, Gödel suffered periods of mental instability and illness. Following the assassination of his close friend Moritz Schlick, Gödel had an obsessive fear of being poisoned; he would eat only food that his wife, Adele, prepared for him. Late in 1977, she was hospitalized for six months and could subsequently no longer prepare her husband's food. In her absence, he refused to eat, eventually starving to death. He weighed 29 kilograms (65 lb) when he died. His death certificate reported that he died of "malnutrition and inanition caused by personality disturbance" in Princeton Hospital on January 14, 1978. He was buried in Princeton Cemetery. Adele's death followed in 1981.
Personal life
Religious views
Gödel was a theist in the Christian tradition. He believed that God was personal, and called his philosophy "rationalistic, idealistic, optimistic, and theological".
Gödel believed firmly in an afterlife, saying, "Of course this supposes that there are many relationships which today's science and received wisdom haven't any inkling of. But I am convinced of this [the afterlife], independently of any theology." It is "possible today to perceive, by pure reasoning" that it "is entirely consistent with known facts." "If the world is rationally constructed and has meaning, then there must be such a thing [as an afterlife]."
In an unmailed answer to a questionnaire, Gödel described his religion as "baptized Lutheran (but not member of any religious congregation). My belief is theistic, not pantheistic, following Leibniz rather than Spinoza." Of religion(s) in general, he said: "Religions are, for the most part, bad—but religion is not". According to his wife Adele, "Gödel, although he did not go to church, was religious and read the Bible in bed every Sunday morning", while of Islam, he said, "I like Islam: it is a consistent [or consequential] idea of religion and open-minded."
Legacy
The Kurt Gödel Society, founded in 1987, was named in his honor. It is an international organization for the promotion of research in logic, philosophy, and the history of mathematics. The University of Vienna hosts the Kurt Gödel Research Center for Mathematical Logic. The Association for Symbolic Logic has invited an annual Kurt Gödel lecturer each year since 1990. Gödel's Philosophical Notebooks are edited at the Kurt Gödel Research Centre which is situated at the Berlin-Brandenburg Academy of Sciences and Humanities in Germany.
Five volumes of Gödel's collected works have been published. The first two include his publications; the third includes unpublished manuscripts from his Nachlass, and the final two include correspondence.
in 2005 John Dawson published a biography of Gödel, Logical Dilemmas: The Life and Work of Kurt Gödel (A. K. Peters, Wellesley, MA, ISBN 1-56881-256-6). Gödel was also one of four mathematicians examined in David Malone's 2008 BBC documentary Dangerous Knowledge.
Douglas Hofstadter wrote the 1979 book Gödel, Escher, Bach to celebrate the work and ideas of Gödel, M. C. Escher and Johann Sebastian Bach. It partly explores the ramifications of the fact that Gödel's incompleteness theorem can be applied to any Turing-complete computational system, which may include the human brain.
Lou Jacobi plays Gödel in the 1994 film I.Q.